串联水库群弱耦合条件下实时防洪调度方法研究

李 颖，王 斌，徐孙钰，朱非林，本梦雪，钱心缘，钟平安

（河海大学 水文水资源学院，江苏 南京 210098）

0 引 言

水库防洪调度领域的研究重点大体包括建模理论［1］、求解方法［2］以及风险决策［3，4］等方面。随着水文预报精度的提高、有效预见期的延长和计算机技术的进一步发展，调度研究历经了从单库拓展到库群，从经验逐渐向优化［5］的过程，水库群防洪联合调度成为重要的非工程防洪措施，也是调度领域的研究热点［6-8］和数字孪生流域中防洪“四预”的核心技术［9，10］。水文、水力和库容补偿［11］是水库群联合调度的物理基础。在此方面，李安强［12］等基于大系统分解协调原理，以溪洛渡、向家坝和三峡三库为研究对象，从水库防洪库容分配的角度，研究了如何做协同防洪联合调度；康玲［13］等以长江上游五座水库组成的防洪系统为研究对象，考虑不同防洪库容对水库安全的影响程度，构建了基于系统非线性安全度策略的水库群防洪库容分配模型，弥补了线性安全度策略的不足；钟平安［14］等提出并联结构水库群防洪库容分配模型，采用轮库补偿法指导调度次序，以实现水库群的空间协同；顿晓晗［15］等为实现三峡水库的实际防洪调度需求，分析了汛期不同时段防洪风险，研究了上下游水库间防洪库容分配及其互用性问题。

串联水库群间的水力联系是复杂多变的［16］，由于洪水传播时间造成的滞时影响以及洪水在两库之间的坦化变形作用，给串联水库群实时防洪调度模型的建立和求解都造成很大困难。在调度期内，上一级水库出流只有部分过程能够在下一级水库同期内响应，相当部分在调度期外滞后反映，可见水流滞时会造成上下级水库之间在调度期内产生水量不平衡的问题，上下库之间的水力联系被削弱了，耦合程度降低，本文称之为“弱耦合”。国内外对串联水库群水流时滞的研究中，大多简单地将水流滞时看作不变的常数，将上库泄流等值平移传播时间后作为下库的部分入库［17］，虽然有一些考虑传播过程坦化作用的研究，也没有提出有效的方法来求解防洪调度模型［18，19］。因此，进一步开展水流时滞的串联水库群实时防洪调度建模和求解方法研究，具有重要的实用意义。

研究以具有公共防护点的串联水库群为背景，基于防洪点最大削峰准则，提出了一种考虑时滞影响的 “弱耦合”条件下串联水库群实时防洪调度方法，并以三库防洪系统为实例，验证方法的有效性。

1 串联水库群实时防洪调度模型

对于n座水库，n个防洪点的串联水库群，见图1。图中，Ri，i= 1，2，…，n，表示第i座水库；Di，i= 0，1，…，n，表示第i防洪控制断面；Qi(t)，i= 1，2，…，n，为第i库至第i+ 1 库的区间流量过程，m3/s，其中Q0(t)为第一库的入库流量过程，m3/s。

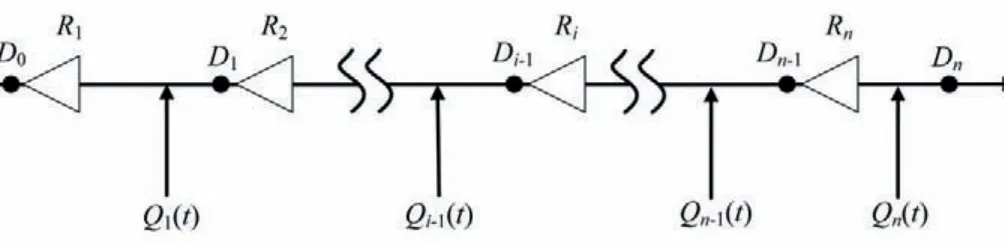
图1 串联水库群防洪系统结构Fig.1 Topological structure of flood control system for cascade reservoirs

1.1 目标函数

考虑区间来水，基于最大削峰准则的串联水库群防洪优化调度的目标函数如下：

式中：q′i(t)为第i库出库流量qi(t)在第i防洪断面的响应流量，m3/s；

1.2 约束条件

（1） 水量平衡约束。

式中：Vi(t)、Vi(t- 1)分别为第i座水库第t时段末、初的蓄水量，m3；QIi(t)、QIi(t- 1)分别为第i座水库第t时段末、初的入库流量，m3/s；qi(t)、qi(t- 1)分别为第i座水库第t时段末、初的出库流量，m3/s；Δt为时段长，h。

（2） 水库水位上限约束。

式中：Zi(t)为第i座水库t时刻的计算水位，m；Zi，max(t)为第i座水库在t时刻允许的最高水位，m。

（3） 水库泄流能力约束。

式中：fi[Zi(t)]为第i座水库在t时刻相应水位下的泄流能力，m3/s。

（4） 出库变幅约束。

式中：∇q为相邻时段允许的最大出库流量变幅值，m3/s，该约束体现泄流变化对下游堤防等防洪设施的影响。

（5） 调度期末水位约束。

式中：Zi(T)为第i座水库调度期末的计算水位，m；Zi，e为第i座水库调度期末的控制水位，m，该约束主要考虑洪水过后的洪水资源利用。

2 考虑时滞的“弱耦合”模型的求解

2.1 水流时滞影响分析

梯级水库群上下库之间存在水力联系，下库来水为上库放水和上下库区间来水之和。当考虑上下库区间的洪水传播时间时，水流时滞将导致上下库流量过程产生错位现象。图2 为三库串联水流时滞示意图，图中T为调度期总时段数，τi为第i库到i+ 1库区间的水流传播时间，mi为第i库泄流对i+ 1库入流的影响时段数（由单位线的时段数确定）。第i+ 1 库前期的入流受第i库调度期之前的放水影响，第i库后期的放水对第i+1库的影响被延迟到调度期外。串联水库群在“弱耦合”条件下进行短期调度，如果优化算法要追求最大削峰效果，可以预见，第i库的调度策略必会加大调度期后期的下泄量，使更多的水转移到调度期外。此策略治标不治本，只变相增加了调度期内的调洪库容，未考虑到对调度期外的库群调度有何影响，实际上实时调度是滚动推进的，水量后移会给后续调洪产生累积风险。因此需构建考虑滞时影响的优化调度模型，并采用适用的方法进行模型求解，这对水库群的实际运行管理有着重要的指导意义。

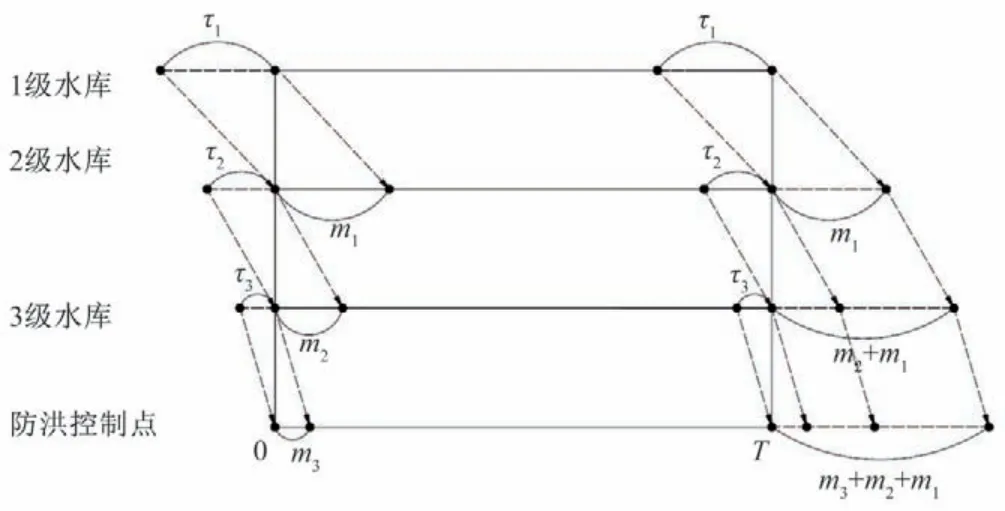
图2 三库串联水流时滞示意图Fig.2 Schematic diagram of flow delay in a three-cascade reservoir system

2.2 “弱耦合”模型轮库迭代求解

由上文分析可知，由于串联水库群的“弱耦合”性，模型如果使用传统方法直接求解，难以得到具有可操作性的最优解。本文提出一种基于信息价值最大化的“不完全”优化思路，通过调度过程迭代，充分利用调度期内上下库之间的水量交换信息，减轻由于时滞造成的调度期内水量不平衡的影响。采用由下而上的反向逐级补偿，得到满足可操作性要求的次优调度方案（“不完全”优化方案）。

反向逐级补偿的计算步骤如下：

（1） 首先对第n库进行单库单防洪点的补偿调度。

①先不考虑 1～n- 1 库的调蓄作用，假定防洪任务完全由第n库承担。第n库的天然来水过程为In(t)，则：

式中：Qni(t)为第i区间的来水Qi(t)在第n库的响应过程，由区间来水经过马斯京根法演算得到。

②以Dn断面为补偿对象，则第n库的最大削峰准则目标函数为：

③考虑第n库的约束条件，采用分段试算法［20］求解得到第n库的最优出库过程q*n(t)。由马斯京根法计算得到q*n(t)在Dn处的响应过程q′*n(t)。

④qDn为Dn处的安全泄量，如果q′*n(t) +Qn(t) ≤qDn，说明在给定条件下，第n库可以单库满足防洪断面Dn的安全泄量要求。这时前n- 1 库按出入库平衡模式调度，即qi(t) =Ii(t)，i=1，2，…，n- 1，以保留足够的防洪库容拦蓄后续来水，防洪断面的防洪要求由第n库满足，计算结束；如果q′*n(t) +Qn(t) ＞qDn，说明第n库无法单独满足Dn断面的安全泄量要求，如图3所示，则按式（10）计算超额流量过程，然后转第（2）步进行上一级水库的反向补偿调度。

图3 防洪断面流量组成图Fig.3 Schematic diagram of flow component on flood control cross-section

（2）为减小超额流量DQn(t)，对第n- 1 库进行补偿调度。计算步骤如下：

①计算第n- 1库的天然来水过程In-1(t)：

式中：Qn-1i(t)为第i区间的来水Qi(t)在第n- 1 库的响应过程，由区间来水经过马斯京根法演算得到。

②第n- 1 库的主要任务是配合第n库进行拦蓄，满足Dn断面的安全泄量。计算第n- 1库的目标出库过程qn-1(t)。

式中：DQ′n(t)为DQn(t)逆流向马斯京根法［21］反演到第n库的坝址过程。QB′n-1(t)为QBn-1(t)逆流向马斯京根法反演到第n-1库的坝址过程。

③第n- 1库补偿调度目标函数为：

④考虑第n- 1 库的约束条件，求解得到第n- 1 库的最优出库过程q*n-1(t)。由马斯京根法计算得到q*n-1(t)在Dn-1处的响应过程q′*n-1(t)。

⑤如果q*n-1(t) ≤qn-1(t)，说明第n- 1库与第n库联合可以满足防洪断面的安全泄量qDn，这时前n- 2 库按出入库平衡模式调度，保留足够的防洪库容拦蓄后续来水，防洪断面的防洪要求由第n- 1 库与第n库联合满足，计算结束；如果出现(t) ＞qn-1(t)，则按式（15）计算超额流量过程，然后转第（3）步进行上一级水库的反向补偿调度。

（3）以此类推，直到计算出第1库的最优出库过程q*1(t)。

（4）特殊情况处理。

①当第1 库的q*1(t) ＞q1(t)，说明在给定约束条件下所有水库联合补偿，也不能满足防洪控制断面的安全目标qDn，其差值DQ1(t) = max[q*1(t) -q1(t)，0]有两种处理方法，当下游安全泄量qDn尚有上升空间时，可加大安全下泄值；当下游安全泄量没有上升空间时，可根据防洪形势分析，提高关键水库的上限水位约束。

②当第1库的最优出库过程q*1(t)小于第1库的目标出库过程q1(t)，则取q*1(t) =q1(t)，腾空第1库的库容迎接后续来水。

计算步骤的逻辑全过程如图4所示。

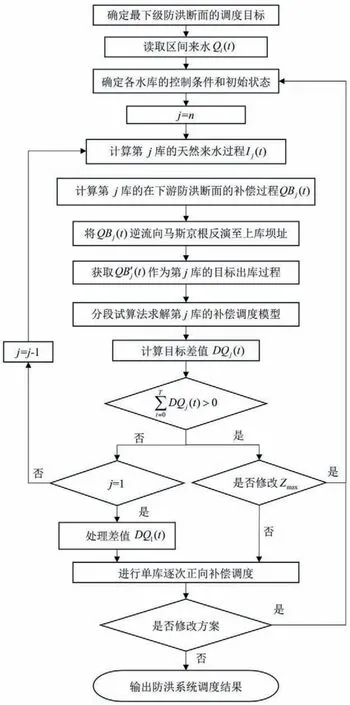
图4 弱耦合防洪模型求解流程图Fig.4 Algorithm flow-chart of weak-coupling flood control model

3 应用实例

3.1 计算条件

江西省北潦北河流域的集水面积为496 km2，境内罗湾水库、洪屏水库、小湾水库三座中型水库呈串联结构，仁首是下游主要防洪断面，如图5所示。

图5 北潦北河水库群概化图Fig.5 Diagram of cascade reservoirs on the northern tributary of the Beiliao River

流域内各水库目前的调度方式见表1。

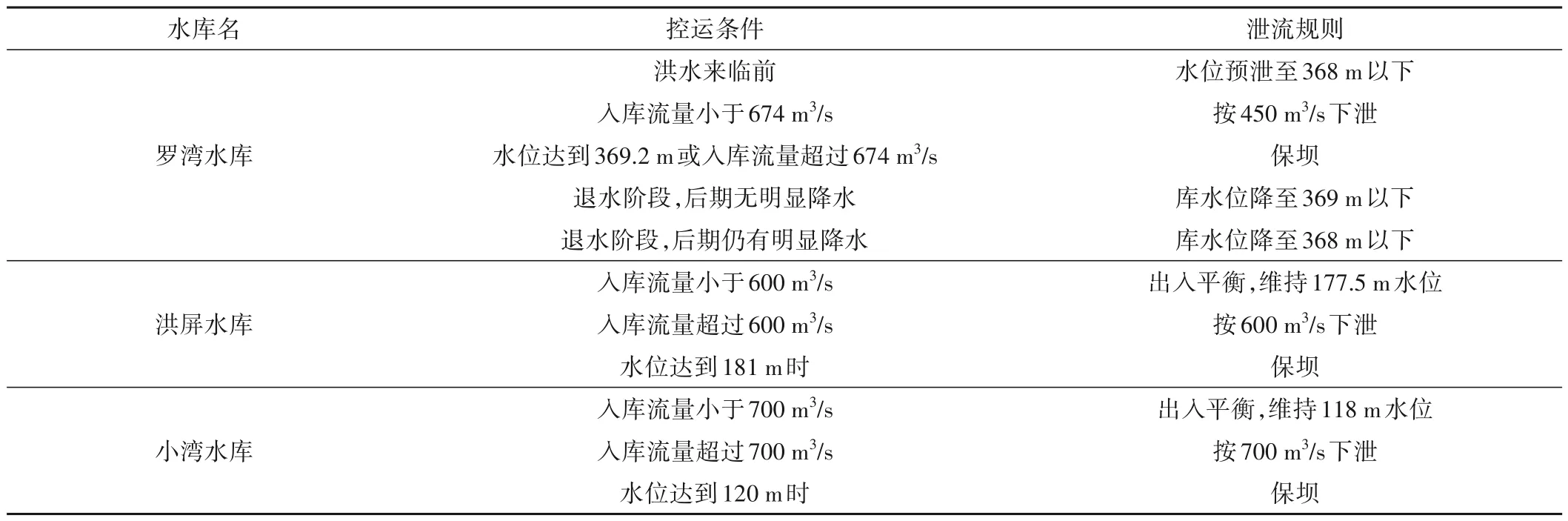
表1 三库现有调度规则Tab.1 Existing scheduling rules of three reservoirs

为了方便计算，我们将洪屏水库库尾当作罗湾水库的虚拟防洪点，将小湾水库库尾当作洪屏水库的虚拟防洪点。采用72 h 为调度期，1 h 为时段长。选取不同量级的三场洪水开展模拟调度，根据记录的实际防洪形势，设定各场洪水调度的约束条件见表2。

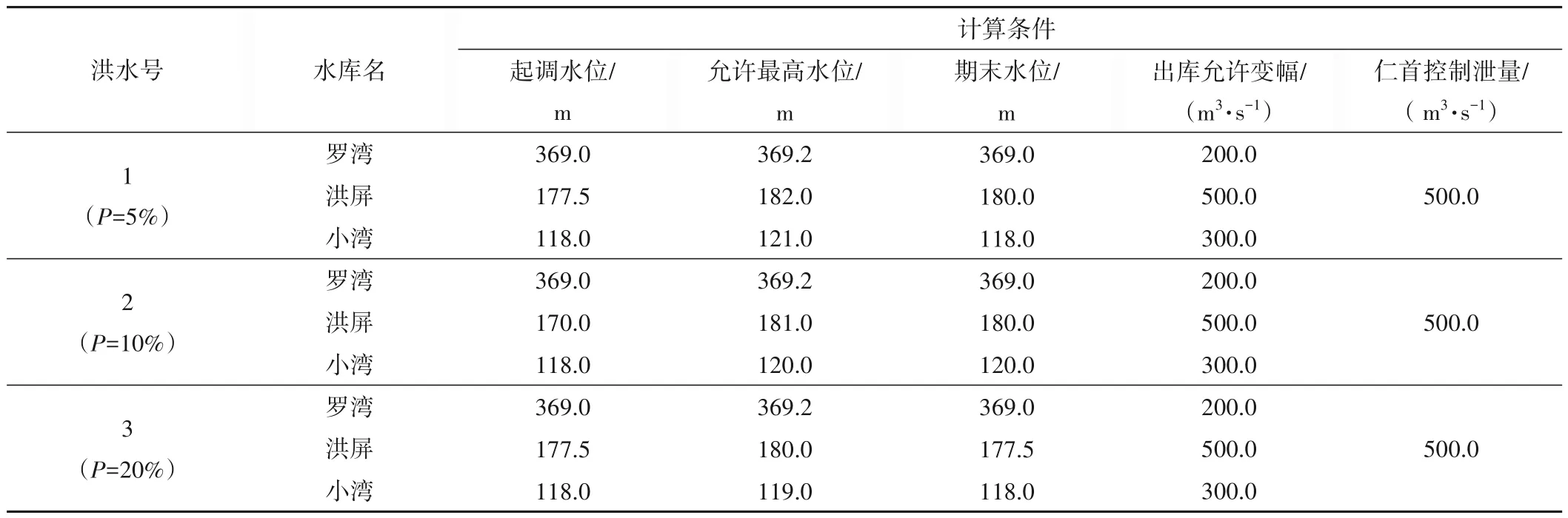
表2 三场洪水计算条件Tab.2 Parameters for operation simulation in three flood events

3.2 结果分析

表3 为三场洪水最优调度方案的基本特征，反映了以下基本规律：

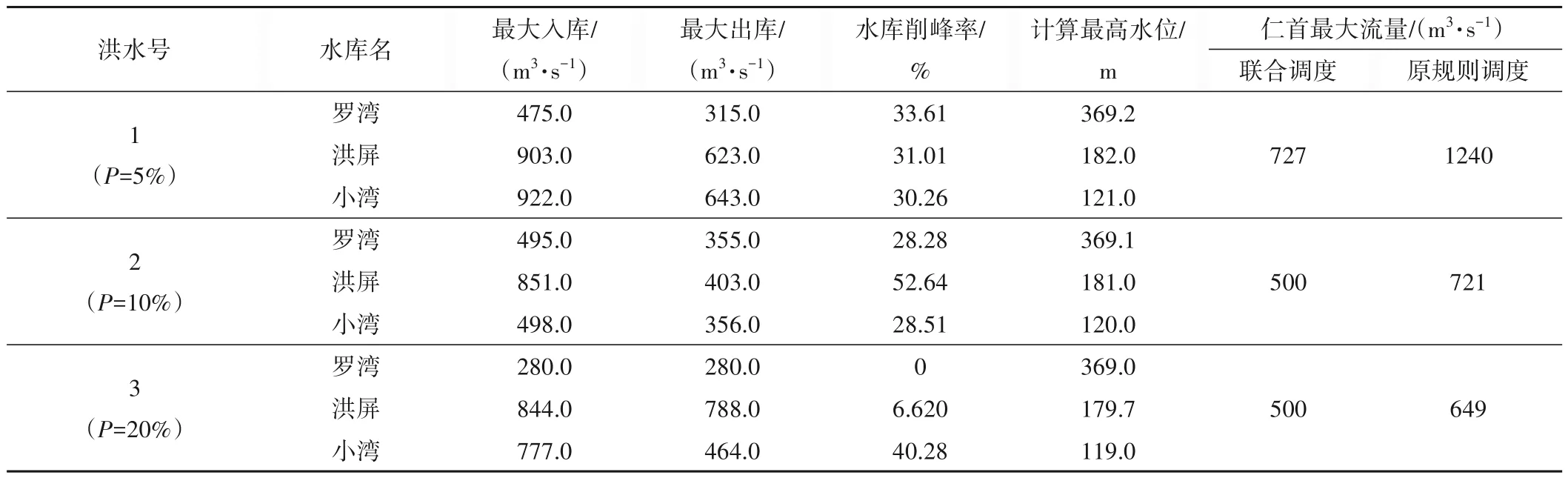
表3 三库调度方案基本特征表Tab.3 Characteristics parameters of three reservoirs in the flood control operation scheme

（1）对于1 号洪水（P=5%），三库的计算最高水位分别为369.2、182、121 m，均达到了允许最高水位（见表2），三库均发挥了较好的削峰作用，水库削峰率分别达到33.61%、31.01%、30.26%，仁首的联合调度最大流量为727 m3/s，远小于原规则调度1 240 m3/s，但仍超过了下游断面安全泄量值500 m3/s，超额部分主要是上游小湾出库造成的［见图6（b）］。这种计算结果体现了水库安全优先的原则，同时给出了防洪控制断面的最好削峰效果，给决策者提供决策参考。如果后续来水的不确定性较高，为了保障水库的绝对安全，决策者可能会选择应急措施，保障防洪断面防洪相对安全；如果水库尚有调蓄潜力，决策者可能会选择抬高某些水库的上限水位，以减少或消除下游防洪断面的防洪压力。

图6 各场洪水下仁首断面流量过程Fig.6 Flood process on Renshou cross-section during different flood events

（2）对于2 号洪水（P=10%），仁首的联合调度最大流量为500 m3/s，小于原规则调度721 m3/s，且补偿目标得到了较好满足［见图6（b）］。洪屏、小湾两库的计算最高水位分别为181、120 m，达到了其允许最高水位（见表2），两库发挥了较好的削峰作用，水库削峰率分别为52.64%、28.51%。罗湾水库发挥了部分的调节作用，削峰率达到28.28%，同时计算最高水位369.1 m比允许最高水位低0.1 m，为拦蓄后续来水留有空间。在三座水库中，洪屏水库的削峰率较大，由于其起调水位较低，较大的防洪库容和调度初期腾出的预泄库容共同拦蓄洪水，能够大幅削减入库洪峰。

（3）对于3号洪水（P=20%），仁首达到的联合调度最大流量为500 m3/s，小于原规则调度649 m3/s，且补偿效果较好［见图6（c）］，水库削峰率分别为0%、6.62%、40.28%，洪屏和小湾水库联合完成了防洪断面的补偿任务。小湾水库计算最高水位达到其允许最高水位119 m，发挥了主力错峰补偿作用；洪屏水库发挥了部分的调蓄作用，预留0.3 m 的库容用于拦蓄后续洪水；罗湾水库实现出入库平衡，保持当前水位不变，预留库容拦蓄后续来水，应对防洪系统不确定性。

（4）图6（d）中，天然来水是完全不考虑水库拦蓄作用的3号洪水直接在仁首断面形成的洪水过程，可以看出，对比原有调度规则，水库群联合调度的削峰作用是显著的，3号洪水削峰率达到了46.65%，这体现了水库群的防洪效益。

由上可见，本文提出的方法，可以较合理地体现不同场景下的防洪调度特点，具有较好的适应性。

4 结 论

以江西北潦北河流域为研究对象，提出了基于信息价值最大化的次优化调度思路，实现弱耦合条件下的防洪联合调度，提出了超额水量由下而上的反向逐级消纳机制和计算流程，并采用最大削峰准则建立补偿调度模型。多个算例的结果表明，该方法适应性和实用性较强，下游断面最大径流较天然来水状态下的最大径流平均降低了48.83%。与原来的调度规则相比，库群联合调度具有更大的削峰效益。库群系统通常能够消纳中小洪水，在大洪水发生时，通过对各个水库提前泄流，使水库水位降低，增加库群的防洪库容，可以有效缓解下游防洪压力。

实际调度过程中来水是不确定的，本文没有考虑预报不确定性对优化调度的影响，加入不确定性分析以指导调度决策，是下一步需要开展的研究。