基于高精度模拟数字转换器的输出异码判别方法

孙凤梅，丁 柯，付天豪

（中科芯集成电路有限公司，江苏 无锡 214072）

模拟数字转换器（Analog to Digital Converter，ADC）应用在数据采集、精密工业测量、语音波段和音频及高速控制回路等领域。随着ADC 的分辨率和速度的提高，测试要求变得更加严格，测试成本的升高，将增加终端用户市场的成本，并迫使电子制造商提供具有竞争力的价格。

本文首先介绍了ADC 的码密度直方图静态参数测试方法，针对输入刺激存在转换异常数字码，提出基于码密度直方图的高精度ADC 对比检验法。测试实验中输入采用正弦激励，结合高精度对比ADC 并根据异常码的正态分布尽可能地去除误码，从而获取更加合理的静态参数。

1 静态参数测试技术

1.1 ADC 测试

在生产测试中常用静态测试参数来衡量ADC 的性能。静态参数有积分非线性（Integral Non-Linearity，INL）、微分非线性（Differential Non-Linearity，DNL）、失调误差等。DNL 和INL 反映了ADC 的传输特性，是最重要的静态参数[1]。

1.2 静态参数

静态参数反映了ADC 的自身性能，音视频、微弱信号检测等应用重点关注的就是ADC 的静态参数，DNL 和INL 的测量方法一起决定了ADC 的静态特性性能。在ADC 实际传输曲线中，每个输出代码对应的输入电压宽度称为码宽（Least Significant Bit，LSB），DNL 定义为

式中：Vn为数字输出第n 个编码位对应的幅值。对于理想的ADC，DNL=0，此时每个码宽电压1 LSB=VF/2N（其中，VF 是满量程电压，N 是ADC 的分辨率），当DNL 误差小于或等于-1 LSB 时，表明实际的传输函数出现了失码现象。ADC 的INL 是指在失调、增益误差被校正后，实际的传输曲线偏离理想中心线的程度

DNL 和INL 的基本测试方法为：

1）逐步调整输入电平，找出输出码由i-1 跳变为i时的输入电平Vi。

2）继续调整输入电平，找出输出码由i 跳变为i+1 时的输入电平Vi+1，则输出码为i 时的实际码宽为Vi+1-Vi。

3）利用式（2）求得DNL，通过对DNL 的积分运算求得INL。

2 测试方法

在对ADC 的静态参数进行测试时时钟抖动、信号驱动能力、电源噪声串扰等外部环境多个因素对测试结果有影响，容易导致精度较高的ADC 的性能特性下降，从而增加了ADC 性能测试的难度[2]。

虽然采用自动测试设备能够对ADC 的各项参数进行很好测试，但是国内自动测试设备研发尚处于初步阶段。随着ADC 采样率与精度的不断提高，对测试设备采样率与精度的需求也在不断提高，因此也有不少人从应用工程上实现对ADC 的静态参数测试评价方法[3-4]。近年来测试成本逐步上升和硅片成本逐年降低，因此有必要去探索并分析更加可取的测试方案。

2.1 码密度直方图测试

早期测试常用码密度直方图技术对ADC 静态参数进行分析。ADC 对周期模拟输入信号进行随机采样，不同数字码输出的出现次数被称为码密度。统计ADC 的输出数字码及其出现次数画直方图。在直方图测试中，每个数字码称为码箱（Code Bin），根据码箱中的码密度数据可以估计出ADC 的静态特性参数。

2.1.1 斜坡直方图

斜坡直方图测试方法是ADC 静态参数测试最主要，也是最有效的方法。如果输入的信号源是斜波，因为输入电压在每个电压幅度上都是等概率的，则理论上待测ADC 的每个输出数字码也是等概率的。但是斜坡发生器作为单斜ADC 结构中最重要的模块，其能否产生线性度较好的斜坡电压对整个ADC 至关重要[5]。

斜坡直方图测试的过程如下[6]。

1）提供一个模拟输入信号。输入最低范围要低于待测试最低值的10%～15%，输入最高范围要高于待测试最高值的10%～15%，以便覆盖全部待测试数字码范围。

2）捕获原始输出的数字信号。

3）整理出输出代码以创建一个直方图。然后计算出INL 和DNL。

定义实际ADC 第n 个数字码出现的次数为Pi（n）；理论ADC 第n 个数字码出现的次数为Pj（n）;则根据式（1）可知

2.1.2 正弦波直方图

由于斜坡信号是由基波和其谐波分量叠加组成，而相比于斜坡信号，正弦频率单一。因此在后续对ADC 精度进行静态参数测试中，有不少研究者选择正弦信号作为待测ADC 的输入[7-8]。如果采用任意波形发生器，内置的滤波器会滤除掉斜坡信号的高频分量，从而降低线性度，而采用正弦信号就不会有这个担忧。正弦信号作为ADC 动态参数的标准输入信号在测试中也更加具有代表性。虽然采用正弦波信号进行测试使得测试结果分析变得更加复杂，并且需要比采用线性进行测试的情况更多的样本，但测试得到的静态参数精度更加准确。

设正弦波信号频率为fIN、偏置为Vs、幅度为Vp，在t1与t2时刻（t2＞t1）的瞬时，电压分别为Vt1与Vt2，信号在Vt1与Vt2区域内出现的概率密度为P，则

当数字码为0 时，输出电压也为0，则

当ADC数字码为2n-1时，输出的电压为V[2n-1]，因此

当数字码为k，其中k=1，2，…，2n-2，瞬时电压在V[k]与V[k+1]之间时，概率密度P（k）为

并结合式（5）、式（6）计算出DNL、INL。

2.2 基于高精度ADC 对比检验法

采用直方图方法非常具有挑战性，由于在测试期间需要将输入模拟信号通过待测ADC 输出为输出码字，测试结果与时钟抖动、输入源噪声串扰等因素有关，从而增加了ADC 静态参数测试的难度。

虽然给ADC 提供电流驱动与噪声抑制能力更强的基准能够对测试提供更好的保证，但是在降低测试成本情况下更好地探寻测试方法也很有必要。文中提出一种基于高精度ADC 对比检验法，测试流程如图1所示。

图1 基于高精度ADC 对比检验流程图

首先提供一个模拟输入信号，输入信号的精度为m 位，输入范围要覆盖全部待测试数字码范围。设待测的n 位分辨率（m＞n）ADC 在第Ti 时刻采样时，输入刺激信号的瞬时实际电压为V[k]+ΔVTi，m 位高分辨率ADC在相同时刻采样时，输入刺激信号的瞬时实际电压为V’[k]+ΔVTi，其中ΔVTi是输入信号源产生的噪声误差

对应的待测ADC 输出实际数字码为

式中：σTi为环境噪声产生的误差；VFSR为测试ADC 的满幅度输入范围。则

式中：D’Ti为高精度ADC 输出实际数字码。由于V’[k]是由高精度ADC 计算所得，因此理论上

则[9]

式中：CH[i]为前n 个数字码的码箱之和，ΔCH[i]=CH[i＋1]-CH[i]，当采样点NS足够大时，ΔDTi服从正态分布[10]，通过实际获取码字可获得正态分布均值u（Ti）和标准偏差σ（Ti），并根据3σ 原则可筛除异常数字码，获得更可靠的实验计算结果。图2 为ADC 转换码字错误输出示意图。

图2 ADC 转换异常码字

由图2 可知，在Ti时刻ΔDTi=-1，Ti 时刻属于误码的概率较低，由实际输出结果计算得到σ 并根据3σ 准则判断Ti时刻转换的异常码可能不是错误数字码。在Ti+3 时刻ΔDTi=-5，属于误码的概率高，需要根据实际采集的数字码结果获取的σ 判定是否需要删除。

测试所用ADC 为Simulink 10 位ADC 模型，高精度采用Simulink 12 位ADC 模型。设置测试ADC 满量程为3.3 V。由于仿真中高精度比较ADC 是待测ADC精度的4 倍，因此将仿真中10 位ADC 噪声的方差设置成12 位ADC 的噪声方差的4 倍更准确。设置10 位ADC 的噪声均值为0，方差σ=0.04 得到的差值分布结果如图3 所示。

图3 噪声方差σ=0.04 的差值分布

由图3 可知，测试差值分布是服从正态分布的，当增大随机噪声，差值分布仍然是属于正态分布，这与文中推导相符。

3 实验与分析

测试硬件采用STM32F407VET6 款MCU 芯片进行测试。此电路是意法半导体列基于高性能ARM@CortexTM-M4 32 位RISC 内核的MCU，内部可配置12 位、10 位、8 位及6 位分辨率ADC。为了保持尽可能测试条件一致，高精度对比ADC 采用同款MCU，ADC 精度配置为12 位，待测试MCU 的ADC 精度为10 位。测试输入源采用泰克Tektronix AFG31251（250 MHz，2 Gs/s）函数发生器，实验采用正弦波作为测试输入源。在实际对ADC 的静态参数进行测试时，输入刺激需要“略大于”ADC 的输入范围。并且信号频率与采样频率互质，并且采样数公式需要满足

被测10 位ADC 电路，若设置β=0.1 LSB 测试精度，90%的置信水平，则采样数NS≥1 070 678。图4—图5 是采用正弦波作为输入刺激中测试其中一颗8位、10 位ADC 的ΔDTi分布概率分布直方图。

图4 10 位ADC 的ΔDTi 概率分布

图5 8 位ADC 的ΔDTi 概率分布

图4 的ΔDTi数据结果获得的拟合u（Ti）=-0.639 6，σ（Ti）=3.375 16，图5 的ΔDTi数据结果获得的拟合u（Ti）=0.091 893，σ（Ti）=1.836。由于INL 是DNL 的积分结果，下面仅分析INL 的测试结果。图6、图7 和图8是测试不同位数ADC 的INL。

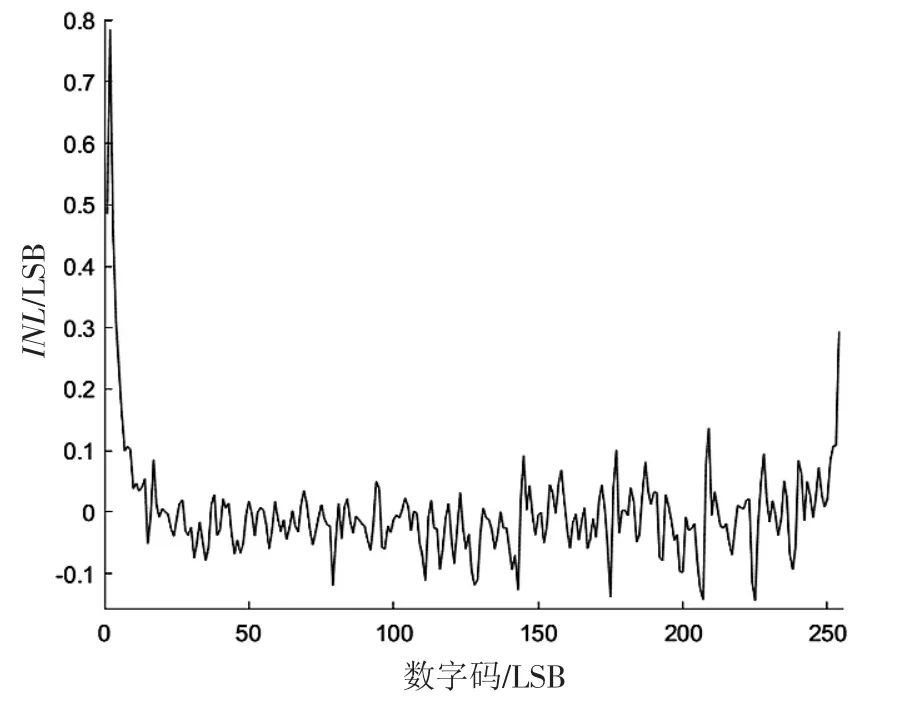
图6 3.3 V 电压测试8 位ADC 精度的INL

图7 3.3 V 电压测试10 位ADC 精度的INL

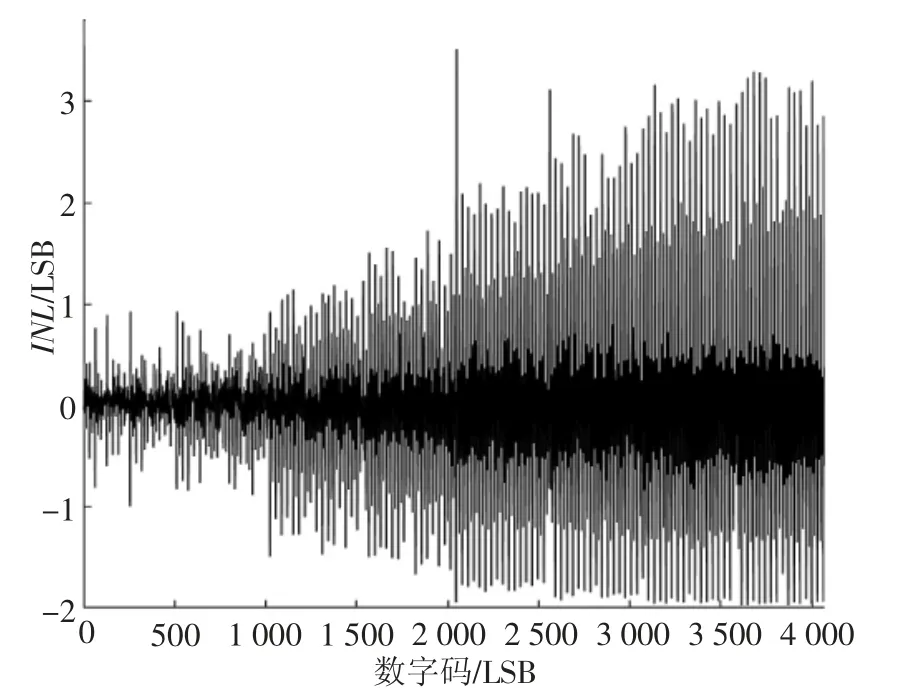
图8 3.3 V 电压12 位ADC 精度的INL

查询测试芯片数据手册可知，在12 位精度下ADC 的积分非线性范围为±3 LSB，本次实验测试在数据手册给定的范围内，因此本次实验测试存在的噪声在可接受的范围内，实验结果可靠性高。

图9和图10是根据3σ判别筛选掉异常噪点后的INL。

图9 去除异常点后8 位ADC 精度的INL

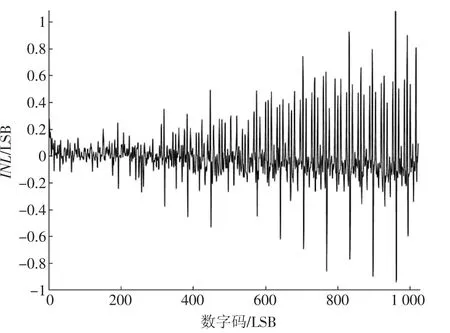
图10 去除异常点后10 位ADC 精度的INL

分别对25 颗实验电路的INLmax进行统计，得到筛选前和筛选后的INLmax均值和标准差结果见表1。

表1 去除噪声点前后INL 均值与标准差对比LSB

由表1 数据可知，去除异常噪声后，INLmax均值和标准差都有所降低，8 位和10 位的ADC INLmax均值相对降低精度分别为（0.742 5-0.679 9）/0.742 5=8.43%和（1.246 9-1.101 3）/1.246 9=11.68%。实验结果表明利用高精度对比检验法去除异常码后获取的静态参数将更加准确。

4 结论

文中提出了当使用码密度直方图法来测量ADC的DNL 和INL 时，通过判别输出码字来去除异常码从而获取更加准确的测试结果。通过理论和实验结果可得，基于高精度ADC 的输出异码判别方法能够较好地去除可能存在的异常输出码。

对比实验结果可知筛选前和筛选后两者结果虽然较为接近，但是后者INL 实验结果优于前者。因此本方法对去除噪声具有一定的可行性。为测试选取合适的数字码提出了指导建议。下一步要考虑的是：

1）测试存在的噪声并非周期性噪声，具有一定的偶然性。

2）实验测试的采样点数刚好在测试条件边界范围，需要满足充足的采样点数以获得更加准确的效果。