水下双层十字交叉组合二面角反射体

2023-08-28陈文剑朱建军孙义诚方芷菲龚新越张淑娟

哈尔滨工程大学学报 2023年8期

陈文剑, 朱建军, 孙义诚, 方芷菲, 龚新越, 张淑娟

(1.哈尔滨工程大学水声工程学院,黑龙江哈尔滨 150001; 2.水声工程国家级实验教学示范中心(哈尔滨工程大学),黑龙江哈尔滨 150001)

水下声学反射体可作为主动声呐性能测试的目标标准体,或作为水下目标回波测试的参考目标。常见的声学反射体有球体、圆柱体和角反射体等[1-3],球体和圆柱体在提高目标强度时需增大体积,而角反射体具有体积小、目标强度大等优点,但单个角反射体不同角度上目标强度的一致性较差,设计组合式角反射体是解决其目标强度角度一致性差的有效途径。角反射体分为二面角反射体和三面角反射体,2个平面垂直组成的角反射体称为二面角反射体,由3个平面互相垂直组成的角反射体称为三面角反射体。在光学和电磁学领域已把角反射体作为反射器使用,并已对角反射体的光和电磁散射问题进行了深入研究[4-5]。近年来,水下声学角反射体也受到了较多的研究和关注。文献[3,6]研究了水下角反射体声散射的计算方法,分析了其目标强度和回波亮点的分布特性;梁晶晶等[7]针对圆形三面角反射体提出了一种目标强度快速数值计算方法;陈鑫等[8]利用结构有限元耦合流体间接边界元法对水下弹性角反射器的远场散射声场进行了仿真计算;陈鑫等[9]利用SYSNOISE软件对水下刚性角反射器远场散射声场进行了仿真计算;罗祎等[10]利用低阻抗泡沫塑料夹层提高角反射器声反射性能;LUO[11]分析了空气腔结构反射面组成的角反射体的反射性能。以上都是对水下单个角反射体的声散射计算方法和特性分析,也有研究人员对多个角反射体组合结构的散射特性开展了一定的研究。孟凯等[12-13]分析了二十面体三角形角反射器的电磁散射特性,多个角反射体组合方式能够在一定程度上满足对全空间大目标强度的需求,但目标强度的角度一致性较差,存在某些角度上目标强度迅速减小的问题。目前,针对以何种方式进行多个角反射体组合,以提高其目标强度-角度一致性的问题还未得到深入研究。

本文针对二面角反射体,提出了计算二面角反射体目标强度的数值-解析计算方法,设计了一种双层十字交叉组合二面角反射体,通过理论计算和实验室水池测量实验,验证目标强度-角度一致性的声学特性。

1 二面角反射体目标强度计算方法

1.1 Knott公式

Knott为分析二面角反射体的电磁波散射特性时,把二面角反射体的回波分解为一次反射波和二次反射波[14],得出了二面夹角可以是[0°,180°]任意角度的二面角反射体散射截面公式,图1为二面角反射体剖面几何示意图。

图1中二面角反射体由2个矩形平面组成,平面的尺寸分别为a×l和b×l,l为宽度。2个面的夹角为2β,入射声波垂直于l且与角平分线的夹角为φ。二面角反射体散射截面为:

(1)

式中:Sa和Sb是2个平面的一次反射;Sab和Sba是声波在2个平面之间的二次反射。具体计算公式为:

Sa=-jka(l/λ)sin(β+φ)exp[-jkacos(β+φ)]·

sin[kacos(β+φ)]/[kacos(β+φ)]

(2)

Sb=-jkb(l/λ)sin(β-φ)exp[-jkbcos(β-φ)]·

sin[kbcos(β-φ)]/[kbcos(β-φ)]

(3)

Sab=-jkb′(l/λ)sin(3β+φ)

exp[-jkb′cos(2β)cos(β+φ)]·

sin[kb′cos(2β)cos(β+φ)]/[kb′cos(2β)cos(β+φ)]

(4)

Sba=-jka′(l/λ)sin(3β-φ)

exp[-jka′cos(2β)cos(β-φ)]·

sin[ka′cos(2β)cos(β-φ)]/[ka′cos(2β)cos(β-φ)]

(5)

式中:

(6)

(7)

α=π-3β

(8)

(9)

根据目标强度与散射截面的关系式[15],可得到收发合置情况下二面角反射体的目标强度:

(10)

1.2 Chen公式

Chen公式从矩形平板的散射出发,利用Kirchhoff近似公式推导了夹角为90°的二面角反射体目标度计算公式,在此基础上进一步得到了夹角在[0°,180°]任意角度的二面角反射体的目标强度[3]。如图2所示的由面Ⅰ和面Ⅱ组成的二面角反射体,面Ⅰ位于xoy平面内,2个矩形平面的夹角为2β,声源和接收点均位于夹角范围内的yoz平面上,在远场条件下可近似认为声波垂直于x轴方向入射。定义rq与z轴的夹角为声波入射角度θ。面Ⅰ的散射声场势函数为:

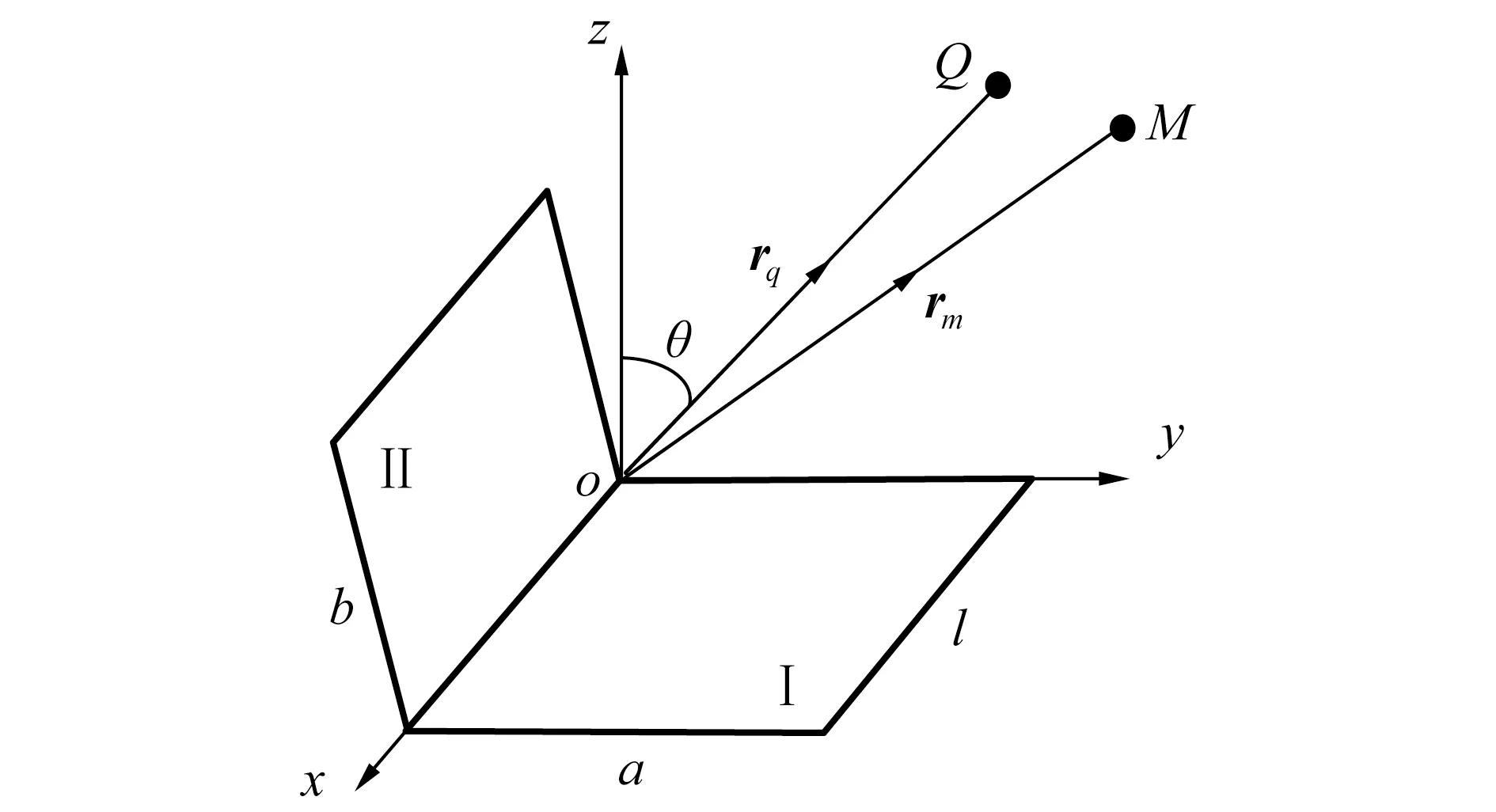
图2 声源和接收点位置Fig.2 Location of sound source and receiving point

(11)

式中:wq0=rq0·n,wm0=rm0·n;rq0和rm0分别是rq和rm的单位矢量;n是面Ⅰ的法向量。

面Ⅱ的散射声场势函数为:

(12)

式中:r′q和r′m分别是在x′y′z′坐标系中声源和接收点到原点的距离;w′q0=r′q0·n,w′m0=r′m0·n;r′q0和r′m0分别是r′q和r′m的单位矢量;n是面Ⅱ的法向量,如图3所示。

图3 x′y′z′坐标系Fig.3 Coordinate system of x′y′z′

面Ⅰ的反射声在面Ⅱ上的散射声场势函数为:

(13)

式中:r′qxu是在x′y′z′坐标系中声源相对于面Ⅰ的镜像点到原点的距离;w′qxu0=r′qxu0·n;r′qxu0是r′qxu的单位矢量;n是面Ⅱ的法向量,如图4所示。

图4 声源相对于面Ⅰ的镜像点Fig.4 Mirror point of sound source relative to plane I

面Ⅱ的反射声在面Ⅰ上的散射声场势函数为:

(14)

式中:rqxu声源相对于面Ⅱ的镜像点到原点的距离;wqxu0=rqxu0·n;rqxu0是rqxu的单位矢量;n是面Ⅰ的法向量,如图5所示。

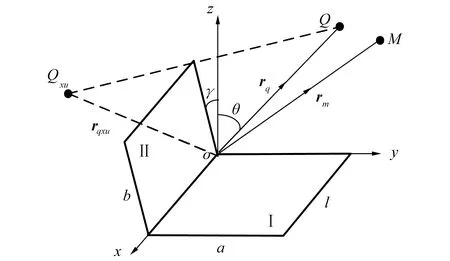
图5 声源相对于面Ⅱ的镜像点Fig.5 Mirror point of sound source relative to plane Ⅱ

以上各式中SⅠ、SⅡ、SⅠ→Ⅱ、SⅡ→Ⅰ的具体计算公式为:

(15)

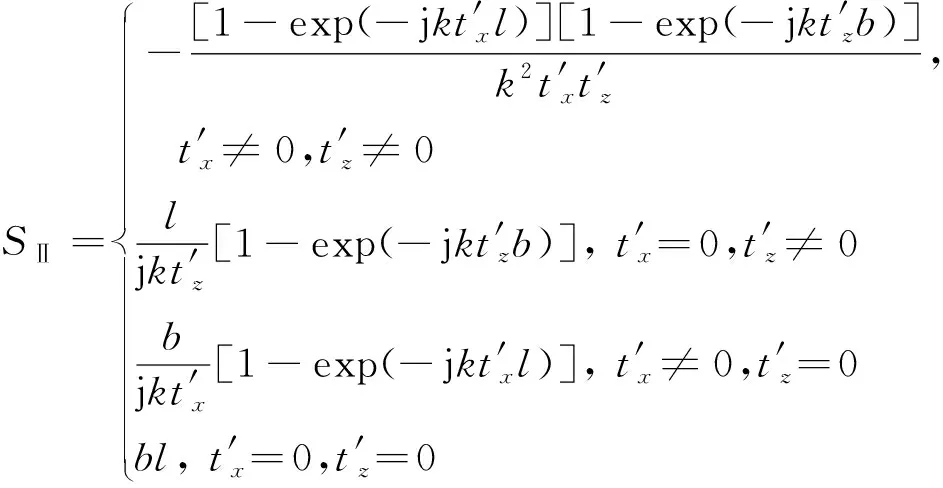
(16)

(17)

式中:当z′Ⅱ≥b时,z′Ⅱ=b。

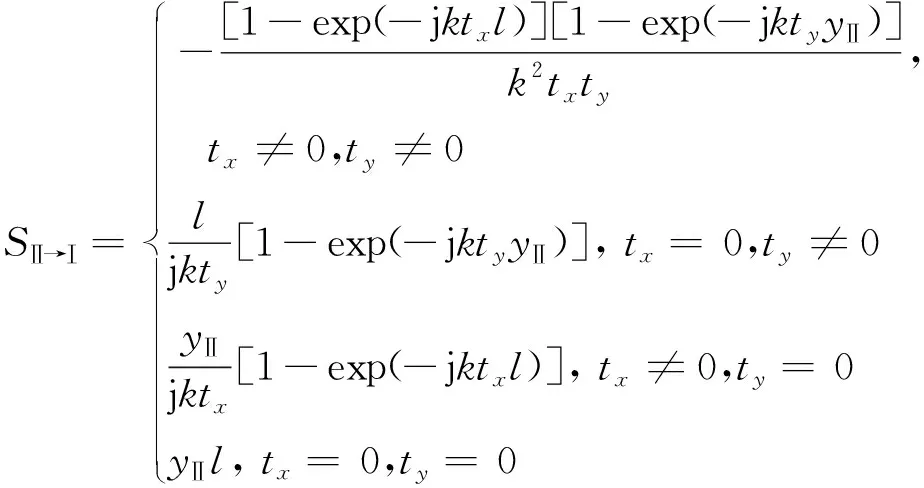
(18)

式中:当yⅡ≥a时,yⅡ=a。

整个二面角反射体散射声场势函数为:

φ=φⅠ+φⅡ+φⅠ→Ⅱ+φⅡ→Ⅰ

(19)

根据目标强度的定义[18],可得到收发合置情况下二面角反射体的目标强度为:

TSTS=20lg(r2|φ|)

(20)

1.3 基于Chen公式的数值-解析计算方法

Knott公式和Chen公式均是计算入射声波垂直两平面交线方向情况下的目标强度,Chen公式相对于Knott公式较为繁琐,但Chen公式是通过设定声源和接收点空间坐标位置进行的公式推导,因此当坐标位置不在yoz平面内时,可进一步得到声波非垂直入射时的目标强度。本文在Chen公式基础上,采用数值和解析相结合的方法求解声波非垂直入射二面角反射体的目标强度。此时反射声波在另一个面上照射区域会出现不规则的多边形,而不是垂直入射时的矩形区域,因此需要采用数值计算方法求解照射区域,然后再求解不规则多边形区域的散射声场。

面Ⅰ和面Ⅱ的散射声场势函数直接采用式(3)和式(4)求解,2个面之间的二次散射需要先求解反射声波照射区域。

对于面Ⅰ的反射声在面Ⅱ上的散射问题,首先进行坐标旋转,使面Ⅱ在x′oy′平面,连接虚源与面Ⅰ得到各条连线与x′oy′平面的交点,形成新的多边形面Ⅰ′,如图6所示,面Ⅱ和面Ⅰ′的共同区域面Ⅲ即是反射声波照射区域。对于面Ⅱ的反射声在面Ⅰ上的散射,连接图5中虚源与面Ⅱ得到各条连线与xoy平面的交点,形成新的多边形面Ⅱ′,面Ⅰ和面Ⅱ′的共同区域面Ⅲ即是反射声波照射区域,如图7所示。

图6 反射声在面Ⅱ上照射的区域Fig.6 Area illuminated by reflected wave on surface II

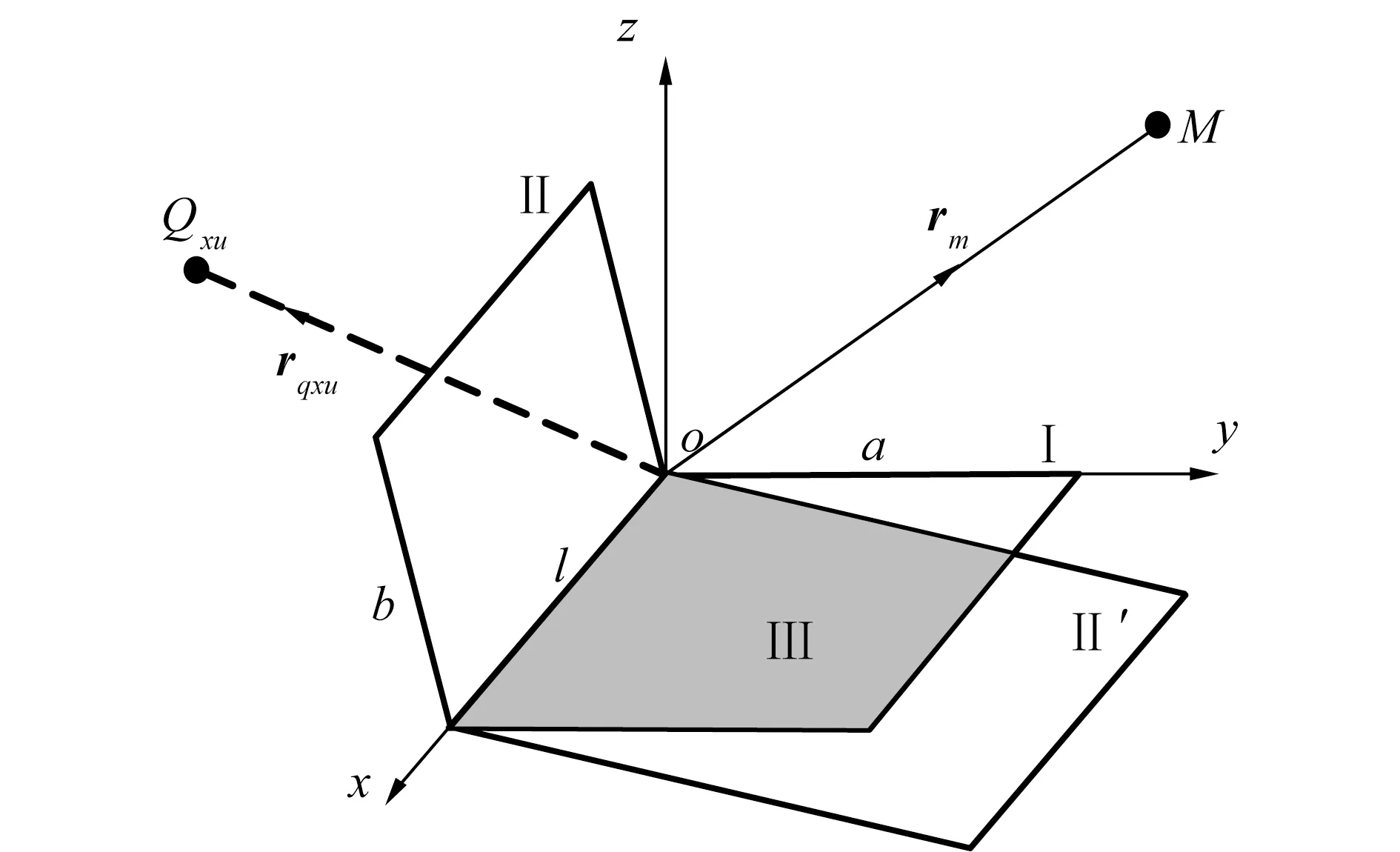
图7 反射声在面Ⅰ上照射的区域Fig.7 Area illuminated by reflected wave on surface Ⅰ

反射声波照射区域求解是2个多边形交集问题,在计算几何中有多种求解方法,最直观的实现步骤为:1)计算2个多边形每条边之间的交点;2)计算包含在多边形内部的点;3)将交点和多边形内部的点按逆时针排序,得出最终的点集,每个点就是交集多边形的顶点。

图6和图7中不规则多边形的散射声场计算,可利用格林定理把面积分变为线积分,然后对线积分分段求解,从而把积分问题化为简单的代数求和问题。Gordon[16]在计算多边形平板的电磁散射时使用该方法,文献[17]将其应用到了板块元积分计算。对于面Ⅲ,有:

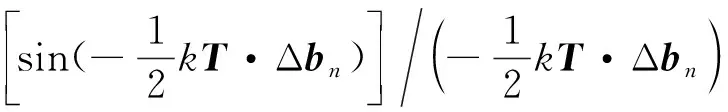
(21)

取二面角反射体尺寸a=b=10 cm,l=5 cm,二面夹角为90°,入射声波频率为80 kHz,图8是分别利用Knott公式、Chen公式和基于Chen公式的数值-解析计算方法计算得到的二面角反射体目标强度结果,其中Knott公式计算时声波垂直于x轴入射,利用Chen公式和基于Chen公式的数值-解析计算方法计算时,声源和接收点处于yoz平面内且为远场,声波与z轴的夹角为θ,声波与x轴的夹角为φ,这里取φ=90°。可以看出,3种方法得到的计算结果一致。

图8 二面角反射体目标强度Fig.8 Target intensity of dihedral corner reflector

Knott公式和Chen公式只适用于声波垂直于x轴入射情况,基于Chen公式的数值-解析计算方法可以计算声波非垂直于x轴入射时的目标强度,取φ∈[80°,100°]角度范围时,二面角反射体目标强度计算结果如图8(b)所示。

2 双层十字交叉组合二面角反射体

在图8(a)中,θ=45°时目标强度值约为-8.5 dB,根据刚性球目标强度计算公式TS=20lg(a/2)[18],半径a≈75 cm的刚性球可达到相同的目标强度。比较而言,二面角反射体具有体积小、目标强度大的优点,但其缺点是随着角度θ偏离45°,目标强度逐渐减小。因此,提出对二面角反射体进行组合设计,使其在θ∈[0°,360°]角度范围内都具有较大的、更加一致的目标强度。

2.1 几何结构

首先将2个矩形平面垂直交叉组成一个十字二面角反射体1,如图9(a)所示;然后将另一个十字二面角反射体沿x轴旋转45°,得到十字二面角反射体2,如图9(b)所示;再将2个十字二面角反射体组合在一起得到双层十字交叉组合二面角反射体,如图9(c)所示。

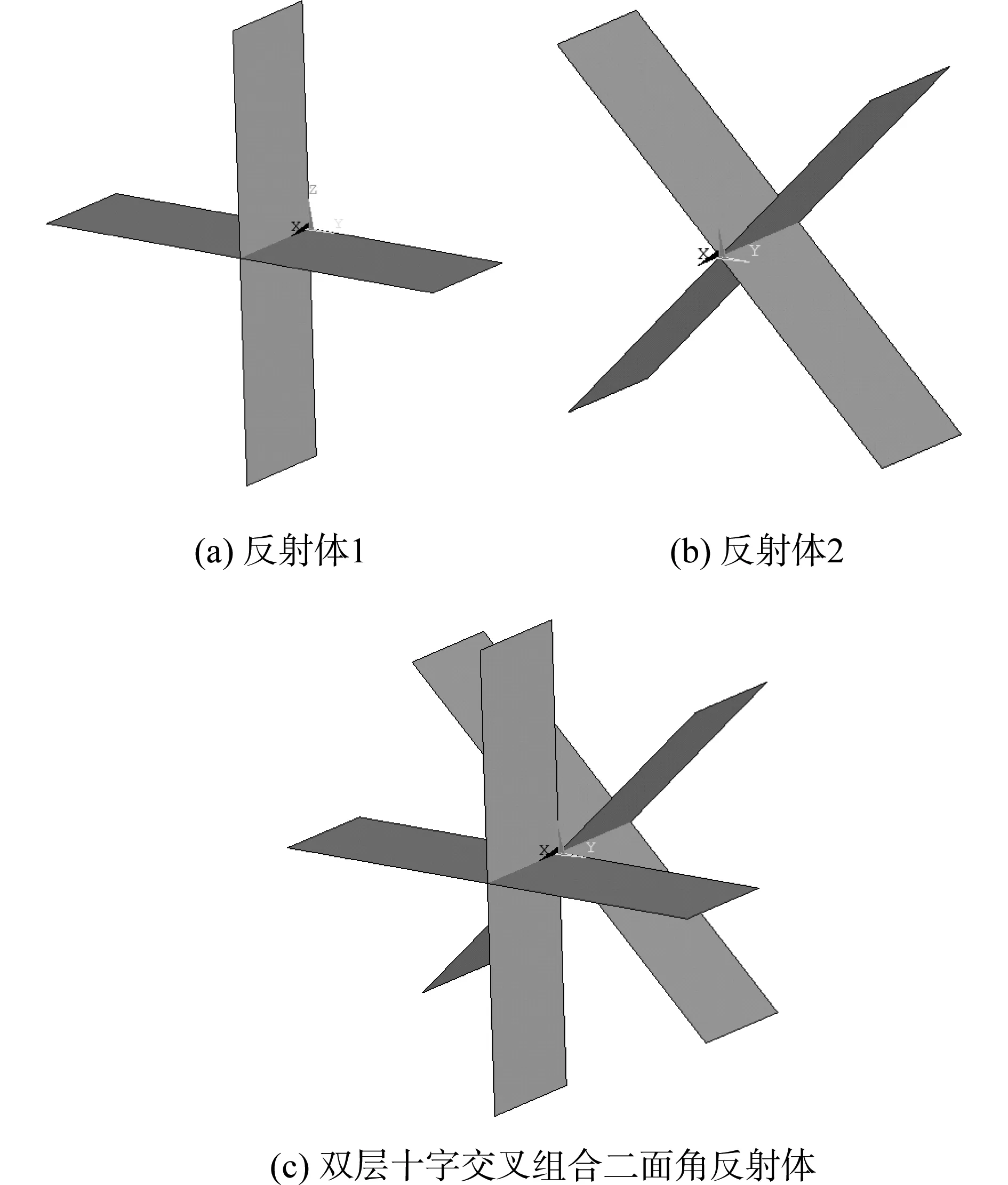
图9 双层十字交叉组合二面角反射体结构示意Fig.9 Structural diagram of double cross combined dihedral corner reflector

2.2 目标强度

图10是φ=90°,θ∈[0°,360°]时对应图9中各反射体的目标强度计算结果,角反射体尺寸和声波频率与图8相同。图10(a)和图10(b)中较宽角度范围的大目标强度是二面角反射体上二次反射回波,较窄角度范围的大目标强度是二面角反射体上反射面的一次反射回波。对于二次反射回波,2个反射体在横轴方向的分布错位了45°,即反射体1的强二次反射回波出现的角度,对应了反射体2的二次反射回波最弱时的角度。因此将2个反射体组合后,组合二面角反射体将会在所有θ角都具有强二次反射回波,如图10(c)所示,图10(c)中存在的较窄角度范围的目标强度峰值是各个反射面的一次反射回波和二次反射回波叠加后的结果。

图10 φ=90°,θ∈[0°,360°],组合二面角反射体目标强度Fig.10 Target intensity of combined dihedral corner reflector at φ=90°and θ∈[0°,360°]

图11是φ∈[80°,100°],θ∈[0°,360°]时双层十字交叉组合二面角反射体的目标强度计算结果。回波信号是2个反射体各自回波信号干涉叠加组成,2个反射体分布在x轴上的不同位置,从而造成2个回波信号存在一定的声程差,因此在φ方向二次反射的强回波出现的角度范围小于图8(b)中的角度范围。图11中在横轴θ角度中的一次反射回波不是在φ方向以90°的对称分布,这是因为这些角度是其中一个反射体的一次反射回波与另一个反射体的二次反射回波叠加后的总的回波,当φ≠90°时,2个回波信号存在声程差,从而产生干涉的结果。

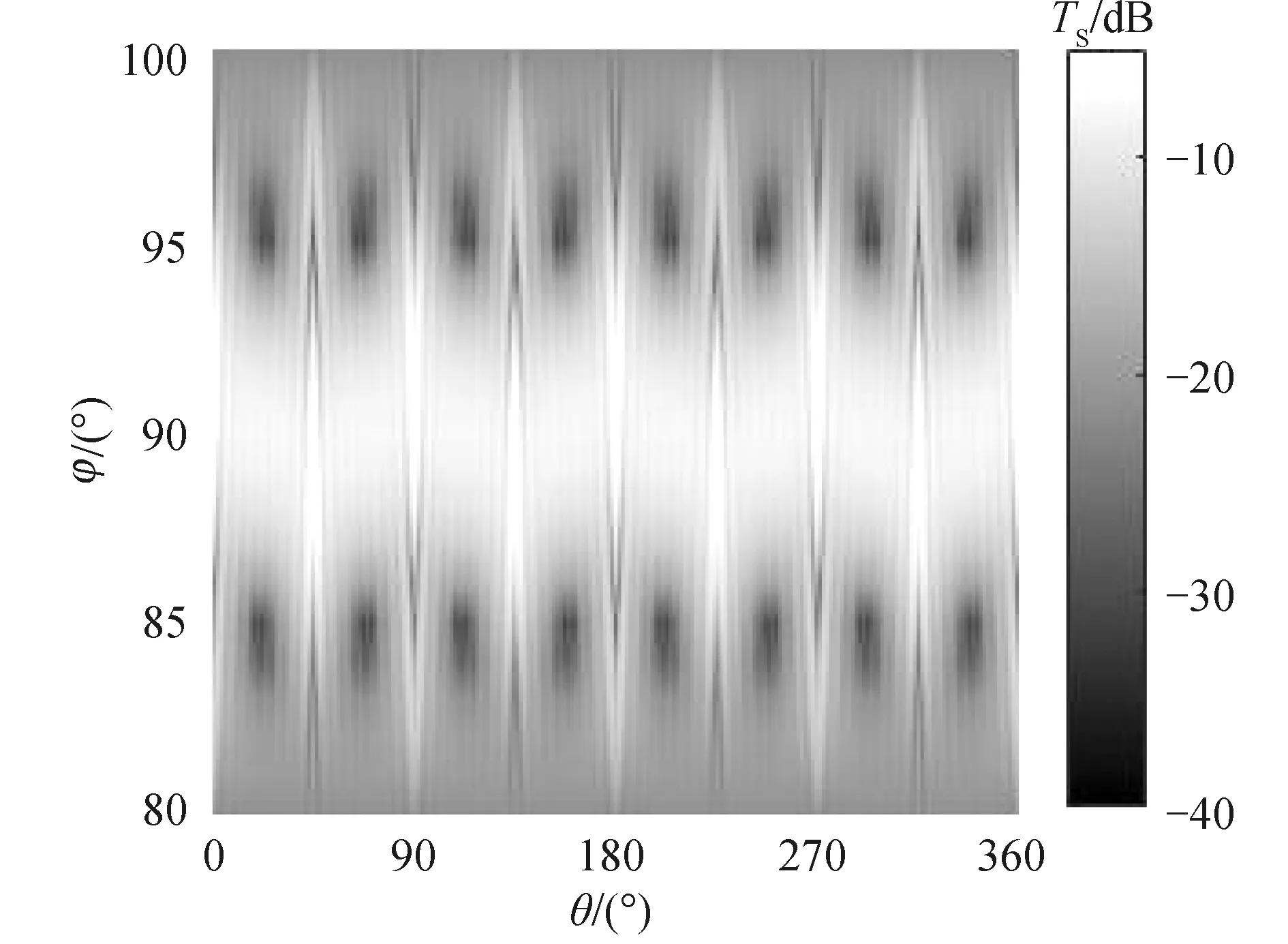
图11 φ∈[80°,100°],θ∈[0°,360°],组合二面角反射体目标强度Fig.11 Target intensity of combined dihedral corner reflector at φ∈[80°,100°] and θ∈[0°,360°]

图10中φ=90°时,可采用Knott公式、Chen公式、或基于Chen公式的数值-解析方法中任一方法分别计算反射体1和反射体2散射声场后相干叠加得到反射体3的散射声场。图11中φ∈[80°,100°]时,采用基于Chen公式的数值-解析方法进行计算,并且在计算过程中进行了反射体1和反射体2之间的相互遮挡。

3 水池测量实验

3.1 实验概况

设计加工了如图12所示的双层十字交叉组合二面角反射体,材质为304不锈钢,钢板厚度1 cm,每个二面角反射体的边长a=b=10 cm,高度l=5 cm。

图12 双层十字交叉组合二面角反射体实物设计图Fig.12 Design drawing of double cross combined dihedral corner reflector

按照“GB/T 31014-2014 声学-水声目标强度测量实验室方法”[19],在实验室水池中测量了双层十字交叉组合二面角反射体目标强度。水下设备布放如图13所示,声源、水听器和反射体处于水面以下相同深度1.50 m,声源至水听器水平距离为1.30 m,声源至反射体中心的距离为3.50 m。声源为波束开角为10°的平面阵,发射信号为频率80 kHz的CW脉冲信号。反射体固定连接在直径为1 cm的钢制圆杆下端,圆杆上端连接至旋转平台。反射体每旋转1°测量一次回波,图14为吊放反射体入水时的状态。

图13 水下设备布放示意Fig.13 Layout diagram of underwater equipment

图14 反射体吊放状态Fig.14 State of reflector during experiment

3.2 目标强度测量结果

实验测量目标强度如图15所示,与φ=90°的理论计算结果相比,两者基本一致,验证了所设计的双层十字交叉组合二面角反射体可以改善目标强度的角度一致性。

图15 实测结果与φ=90°时理论计算结果对比Fig.15 Comparison between measured results and theoretical calculation results at φ=90°

3.3 误差分析

1)测量距离。

在理论计算时收发位置均处于散射波的远场,即收发位置距反射体距离要远大于瑞利距离,但在实验室水池测量时,很难满足该条件。以图8中计算的二面角反射体即组合二面角反射体中的一个二面角反射体为例,计算θ=45°时声源距反射体距离3.5 m条件下,水听器距反射体距离不同时的散射声波以及由此得到的目标强度结果。由于需要计算近场散射,因此在基于Chen公式的数值-解析计算方法中,需要对图2中面Ⅰ和面Ⅱ进行网格划分,采用板块元方法计算一次反射回波;在图6和图7中二次反射的区域面Ⅲ需要再次进行网格划分,即采用声束弹跳方法计算二次反射回波。图16分别是声源距反射体距离3.5 m时不同接收距离的散射声波势函数模值和相应得到的目标强度。由图16(a)可知,接收距离2.2 m约为瑞利距离的6倍;在图16(b)的目标强度结果中,此距离处对应的目标强度为-8.54 dB,图8中远场条件下得到的目标强度为-8.51 dB,两者仅相差0.03 dB,因此测量距离对结果的误差影响可以忽略。

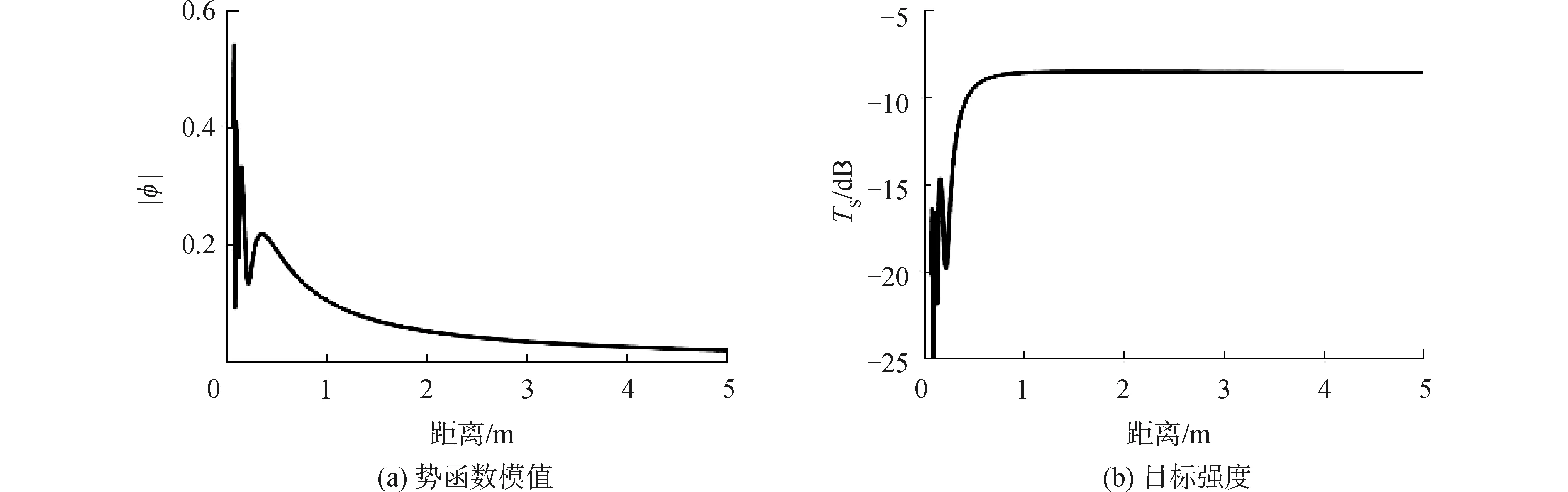
图16 不同接收距离的势函数模值和相应的目标强度Fig.16 Modulus of potential function and corresponding target strength at different receiving distances

2)吊放连杆回波。

实验测量时采用了钢制圆柱杆吊放反射体,吊放连杆的回波也会对测量结果产生影响。由实验布置距离和声源指向性波束宽度,声波照射到连杆的长度约25 cm。仿真计算实验布置条件下连杆的散射声场,将其与反射体的散射声场干涉叠加,结果如图17所示,由于连杆的影响,目标强度增大了约0.20～0.40 dB,平均增大0.35 dB。

图17 反射体和连杆总体的目标强度Fig.17 Target strength of reflector and connecting rod

3)反射体吊放角度。

根据图11中的计算结果可知,反射体目标强度与角度φ有关,在实际吊放时很难保证反射体轴线严格垂直,导致了反射体旋转过程中入射声波并不是严格的按照φ=90°角度入射。图18给出了φ=89°和φ=91°时理论计算结果与实测结果的对比,可以看出,角度φ存在±1°误差时,目标强度会有所减小,φ=89°时平均减小1.05 dB,φ=91°时平均减小1.06 dB。