基于改进灰狼算法的船舶数学模型参数辨识
2023-08-28孟耀张秀凤陈雨农
孟耀, 张秀凤, 陈雨农
(大连海事大学 航海学院,辽宁 大连 116026)
船舶操纵运动数学模型主要分为整体型数学模型、分离型数学模型、响应型数学模型。整体型数学模型需要计算大量的水动力导数,且有的水动力导数物理意义不明确;分离型数学模型起源于日本,在我国运用较广泛;响应型数学模型以舵角为输入,船舶艏向角和转艏角速度为输出,在控制领域运用广泛,且已被应用到了船舶航向、航迹自动保持控制中[1]。船舶响应型模型准确的参数值对于船舶运动状态预报至关重要,其中K、T指数的计算方法有野本标准Z形操纵试验法、回归公式估算法等[2]。早期船舶运动数学模型参数辨识算法有最小二乘[3]、拓展卡尔曼滤波[4]、最大似然估计[5]、反步法[6]等。
随着智能算法及控制理论的发展,多新息理论[7-8]和非线性新息理论[9-10]被应用于传统算法的优化研究,并利用优化后的辨识算法实现了船舶分离型数学模型、船舶响应型数学模型的参数辨识。新息理论的应用使得传统算法的收敛性、精确性提高,预报结果更加贴近于试验数据。除此之外,一些智能算法被应用于船舶数学模型的参数辨识。褚式新等[11]利用粒子群算法对递推最小二乘算法到的参数辨识结果进一步优化,得到更加准确的无人艇响应模型操纵性指数。谢朔等[12]、张心光等[13]利用支持向量机(support vector machine, SVM)在线辨识了船舶响应型数学模型的操纵性指数,证实了SVM是一种有效的在线参数辨识方案。另外,SVM也被应用到其他领域[14-15]。灰狼算法(grey wolf optimizer, GWO)具有参数少、易调节、搜索能力强以及寻优速度快等优点,应用于较多的研究领域[16-17],如机器学习算法的超参数优化[18]、路径规划[19]以及参数辨识[20]等方面,并且在这些应用领域都取得了较好的研究成果。
由于环境干扰、样本数据选择以及算法参数设置不合理等影响,算法的回归精度会降低,辨识的参数会不准确。因此,本文利用改进灰狼算法(modified grey wolf optimizer, MGWO)对辨识参考值进一步优化,使回归预报、参数辨识的结果更加准确。将从高精度航海模拟器中获得的大型油轮的10°/10°、20°/20° Z形试验数据进行处理,并应用SVR和MGWO算法实现大型油轮操纵性指数辨识。为了提高参数辨识的准确度,本文利用支持向量回归(support vector regression, SVR)辨识10°/10° Z形试验数据得到K、T指数的辨识参考值。当参考值不准确时,利用MGWO算法对参考值进行优化。将本文算法得到的辨识结果与基于遗忘因子的递推最小二乘(recursive least squares with forgetting factor, FFRLS)[21]得到的结果进行对比,验证优化后辨识结果的准确性。
1 船舶响应型数学模型
船舶响应型数学模型可以用来描述船舶操纵性能,其反映的是船舶艏向角对舵角变化的响应,在控制领域运用广泛。本文所用一阶和二阶艏向角响应线性方程分别为:
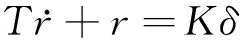
(1)

(2)
令p=T1T2,q=T1+T2,将式(1)和式(2)向前差分离散化,得到:
r(k+1)=a11r(k)+b11δ(k)
(3)
r(k+1)=a21r(k)+a22r(k-1)+b21δ(k)+
b22δ(k-1)
(4)
式中:k为样本序列;a11、a21、a22、b11、b21、b22为待辨识参数,采样间隔h=1 s;n为样本总数,系统的输入输出数据如表1所示。

表1 系统输入输出数据Table 1 System input and output data
表1中,一阶线性响应模型辨识值转换为K、T指数分别为:
(5)
将二阶线性响应型数学模型辨识值转换为K、T:
(6)
2 辨识方法
2.1 支持向量回归
SVR的原理是将样本数据变换到高维特征空间,在高维特征空间中对样本数据进行回归拟合[22]。本文通过建立的输入、输出样本数据(xi,yi),建立高维空间的回归拟合函数,并引入不敏感损失函数及惩罚函数,分别为:
f(x)=ωφ(x)+b
(7)
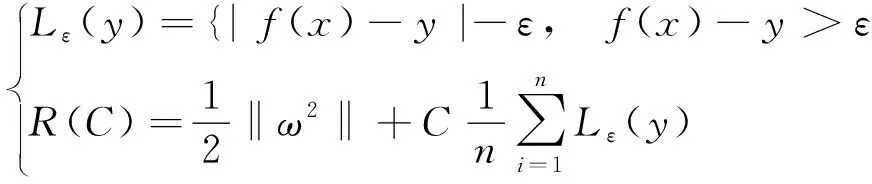
(8)
式中:f(x)为回归拟合函数;ω为权重;φ(x)为非线性映射函数;b为偏置;R为惩罚函数;C为惩罚因子;Lε(y)为不敏感损失函数;ε为不敏感系数;n为样本总量。
引入非负松弛变量ξ、ξ*,得到最小化风险函数fc以求取ω和b:
(9)
(10)
2.2 改进灰狼算法
GWO算法[23]受启发于灰狼捕食猎物的行为,该算法主要包含4个阶段,分别为划分狼群、包围猎物、追捕猎物、攻击猎物。
1)划分狼群:按照适应度值的高低,将狼群划分为4个等级,由高到低依次为α、β、η、ω。
2)包围猎物:对GWO算法的线性收敛因子进行改进,使得该算法的全局搜索能力加强。在包围猎物时,每个灰狼的位置不断更新,更新方式为:
(11)
式中:D是灰狼与猎物之间的距离向量;X是灰狼位置向量;XP是猎物位置向量;A、C是系数向量;a是改进的非线性收敛因子;r1、r2是[0,1]的随机数;i为当前迭代次数;I为最大迭代次数。
3)追捕猎物:在将猎物包围之后,狼群ω由α,β,η领导来追捕猎物,狼群位置得到更新。由于适应度函数值不同,α狼更加靠近于猎物,所以狼群的更新策略应更侧重于α,其次是β,最后是η。改进种群更新策略后的GWO算法为:
(12)
式中:X1是α的更新后的位置向量;Xα是α的位置向量;Dα是α的距离向量;Wα是α的权重;fα是α的适应度值,以此类推。
4)攻击猎物:灰狼完成狩猎,算法得到最优解。
MGWO算法在GWO算法的基础上做出了以下的改进:1)采用非线性收敛因子。GWO算法中收敛因子对算法的搜索能力影响较大,且GWO算法中收敛因子为线性递减的,这种线性减小的策略弱化了算法的全局搜索能力,于是本文对其进行了改进,将线性收敛因子改为非线性收敛因子,全局搜索能力时间变长,使算法前期的全局搜索能力增加,从而有效避免了算法陷入局部极值的情况;2)引入位置更新权重。将灰狼种群的更新策略进行修正,增加位置更新权重,使得灰狼种群位置更加接近于α狼,即更接近于最优解。
2.3 改进灰狼算法验证
为了验证MGWO算法和GWO算法的搜索性能,本文利用Sphere函数(单峰函数)和Rastrigin函数(多峰函数)来测试2种算法的可靠性[24]。设置种群规模为30,最大迭代次数为300,循环做30次实验,2种测试函数都存在最小值0。取30次中的最优值、最差值和平均值作为评判标准,具体的适应度值如表2所示。
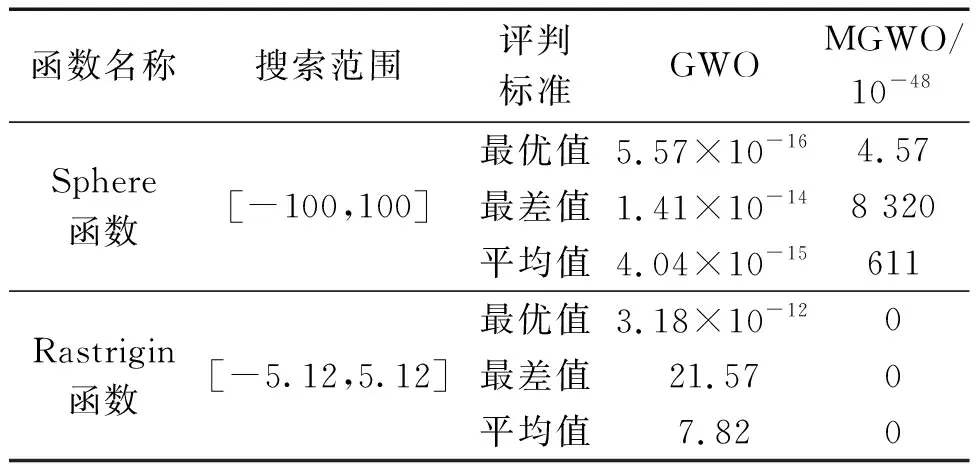
表2 GWO算法与MGWO算法适应度值对比Table 2 The comparison of fitness values between GWO algorithm and MGWO algorithm
3 MGWO优化SVR辨识算法的应用
当SVM用于回归、参数辨识时,被称为SVR,该方法是基于风险最小化原则,适用于小样本数据的学习,已被广泛运用到船舶操纵运动辨识建模与预报中[25]。但是由于数据集的影响(样本的选择)[26-27]或者超参数设置不恰当[25],难免会导致辨识的结果不准确,即由于人为因素或者数据集的原因,会导致SVR辨识结果不理想。因此,当SVR辨识结果精度较差时,本文利用MGWO算法较强的搜索能力对SVR的辨识参数进行范围内优化,使得辨识结果更准确。
本文采用的试验样本数据来自于360°高精度全任务航海模拟器,该模拟器利用6自由度MMG分离型运动数学模型进行解算船舶的运动状态,仿真精度高,性能可靠[28]。在航海模拟器中选择一艘大型油轮进行了10°/10°、20°/20° Z形试验,数据采样周期为1 s。10°/10° Z形试验数据作为训练数据,其仿真时间为931 s;20°/20° Z形试验数据作为泛化性验证数据,其仿真时间为928 s。油轮的主要尺度参数如表3所示。大型油轮方形系数和排水体积较大,从而使得其与普通吨级船舶的操纵性性能相差较大。大洋航行时,大型油轮的舵效、追随性以及航向稳定性较差,对操舵的响应也较为迟钝。因此,基于大型油轮的这些航行特性,对其的操纵性研究可以为驾驶人员安全操舵提供一定的参考。
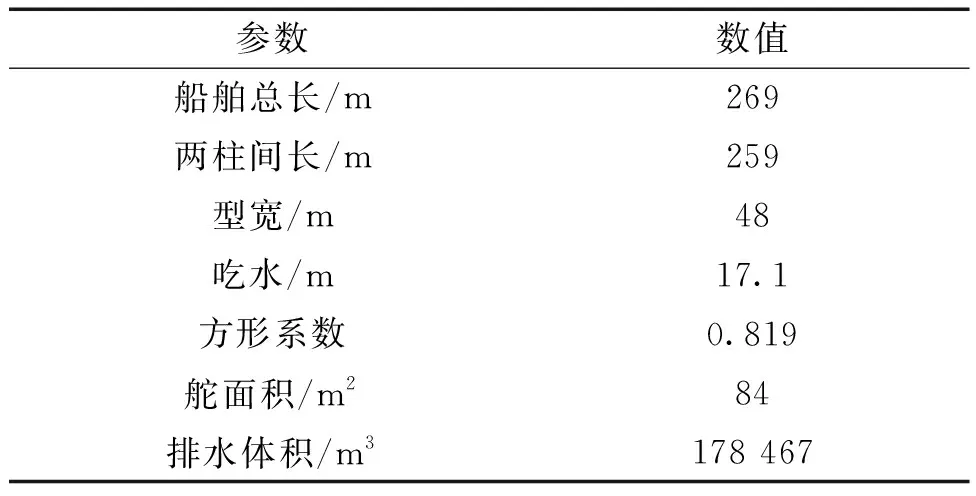
表3 油轮主要尺度参数Table 3 The main dimensions of tanker
3.1 一阶线性船舶响应型数学模型参数辨识及预报
对处理好的10°/10° Z形试验数据,利用SVR进行参数辨识。设置线性SVR的惩罚因子为104,不敏感系数为10-7,得到辨识参考值(a11,b11)。基于SVR辨识得到的参数值,设定MGWO算法的寻优范围。一阶船舶响应模型中的参数寻优的上下限X′min、X′max分别为:
(13)
设置完寻优范围后,对灰狼种群进行初始化,设置初始灰狼个数为500个,最大迭代次数为200次,根据上述的MGWO算法的寻优原理及参数寻优范围,利用均方误差(mean square error, MSE)作为评判标准[29],对辨识参考值进一步优化,并将优化后得到的一阶船舶响应数学模型的辨识参数值与SVR、FFRLS辨识得到的辨识参数值进行对比。其中,FFRLS中遗忘因子设置为0.98。最终的预报结果如图1所示,辨识参数以及适应度函数曲线如图2所示。将辨识得到的参数值转换为船舶响应型数学模型中的操纵性指数,并与野本标准Z形试验理论值进行比较,具体数值如表4所示。
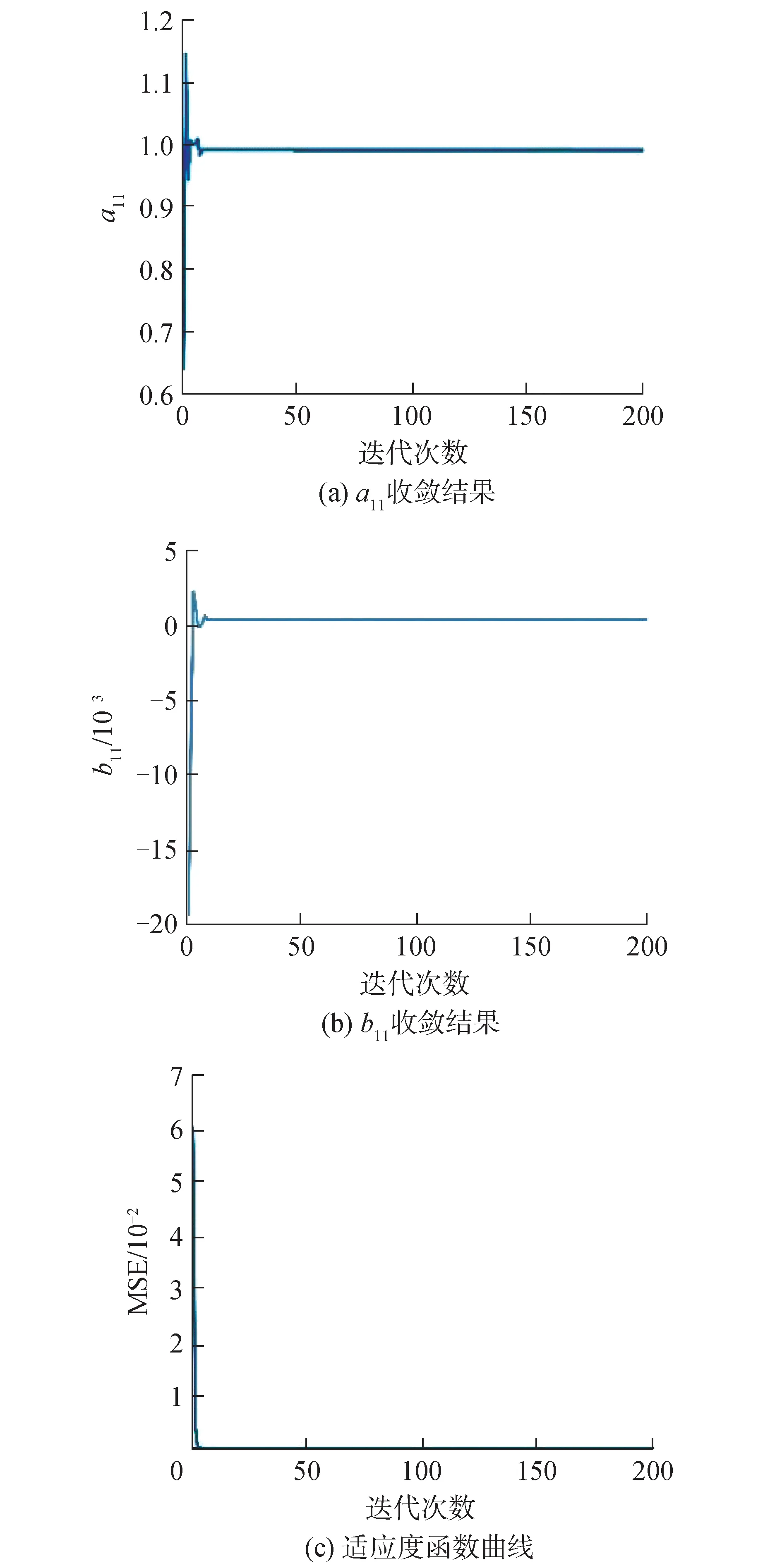
图2 一阶船舶响应型数学模型收敛曲线Fig.2 The convergence curve for first order ship response mathematical model
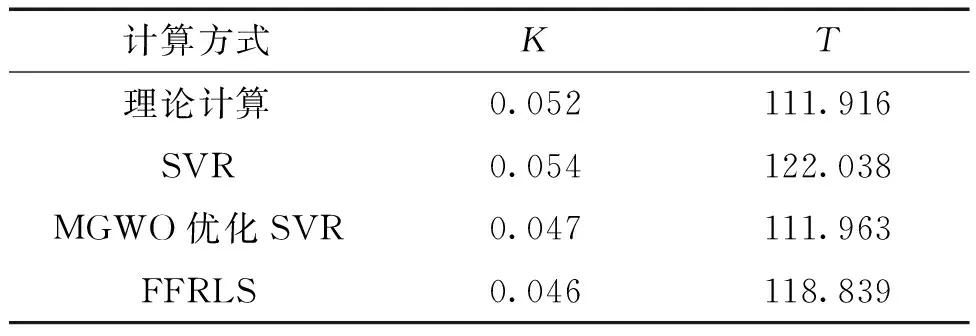
表4 一阶船舶响应型数学模型操纵性指数Table 4 The maneuverability indices of first order ship response mathematical model
航海模拟器是基于6自由度MMG分离型数学模型解算船舶的运动状态并且MMG分离型数学模型与响应型数学模型求解方法有所不同。因此,从操纵性指数验证方面,本文采用的验证方案为:利用野本标准Z形试验得到的理论值进行仿真以得到试验数据,并将辨识得到的参数代入式(1)以得到预报结果。一阶线性船舶响应型数学模型中需要辨识的参数只有2个,参数之间的相互影响较小,从图1中可以看出,3种辨识算法都得到了较好的预报效果,其中,SVR得到的预报结果与仿真试验结果具有较高的一致性,这也证明了SVR是一种有效的建模方式。相较于本文所提算法和SVR,FFRLS的预报效果较差,在经过MGWO算法优化后的预报结果与SVR相近。在艏向角预报结果中,SVR的最大绝对误差(max absolute error, MAE)为1.35°,FFRLS的MAE为4.75°,MGWO算法优化后的MAE为2.75°。从表4可以看出SVR辨识得到的K最接近理论值,但是T与理论值有一定的偏差。
从预报结果中可以看出,SVR得到的预报结果误差较小。本文所提算法的初衷是将预报结果较差的辨识参数进行范围内寻优。根据图2(a)和(b)可知,a11、b11最终分别稳定在1和0附近。
3.2 二阶线性船舶响应型数学模型参数辨识及预报
针对于本文建立的二阶船舶响应型数学模型,为了使FFRLS的辨识结果更加的准确,将FFRLS的遗忘因子值设置为0.99,其他参数不做修正。利用SVR得到辨识参数的参考值,根据参数寻优上下限实现模型参数寻优,得到范围内优化的参数辨识值,辨识参数及适应度函数收敛曲线如图3所示,二阶船舶响应型数学模型的运动变量预报结果如图4所示,二阶船舶响应型数学模型的操纵性指数值如表5所示。二阶船舶响应型数学模型参数寻优的上下限X″min、X″max分别为:

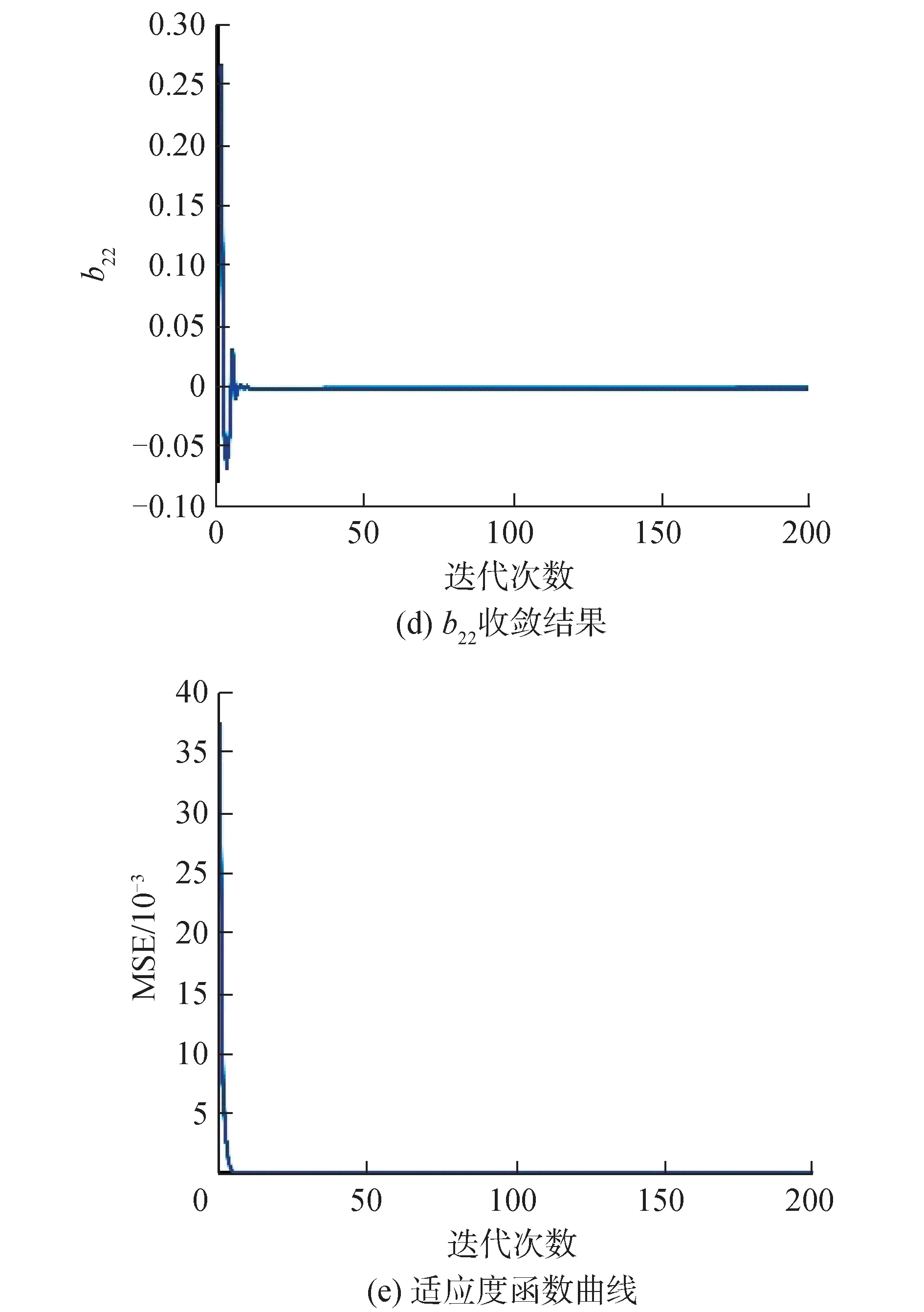
图3 二阶船舶响应型数学模型收敛曲线Fig.3 The convergence curve of second order ship response mathematical model

表5 二阶船舶响应型数学模型操纵性指数Table 5 The maneuverability indices of second order ship response mathematical model
(14)
从图3的参数收敛曲线图中可以看出,a21、a22在参数收敛时发生了振荡并最终收敛于一个定值,但是对MGWO算法的适应度函数值并无影响。
2个参数最终分别稳定于1.6和-0.6附近,b21、b22稳定于0附近。将SVR得到的辨识参数值代入到式(2)进行解算时,方程出现了发散的现象,因此,未将SVR的预报结果列入到图4中。导致SVR辨识参数发散的原因为:1)算法超参数设置的原因;2)训练数据集选择以及构造问题;3)辨识参数较多,辨识参数之间相互影响较严重。
从图4的预报结果图中可以看出,尽管SVR辨识得到参数准确性较低,但是,相较于FFRLS得到的预报结果,经过MGWO算法优化后的预报结果具有较高的精度。这也体现出了所提算法的搜索能力以及收敛能力。将MGWO算法优化后的参数代入到式(2)中,艏向角预报结果的MAE为3.07°。从表5中也可以看出,SVR辨识得到的操纵性指数偏离理论值较大,相对来看,经过优化后的结果更加接近于理论值。
3.3 算法泛化性验证
本文利用MGWO优化SVR的方法辨识了10°/10° Z形试验数据,得到了一阶、二阶船舶响应型模型的参数辨识值。在一阶、二阶船舶响应模型辨识实验中,验证了所提算法的可行性以及有效性,即在2组辨识实验中,所提算法都得到了较好的预报结果。为了验证算法的泛化性能,利用本文算法得到的辨识参数结果,代入一阶、二阶船舶响应型数学模型中,获得2种不同模型下的20°/20° Z形试验预报数据,预报结果如图5、6所示。
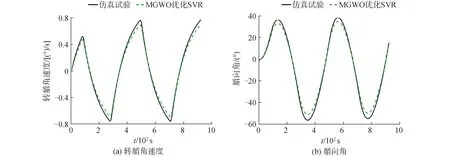
图5 一阶船舶响应型数学模型泛化性预报结果Fig.5 The generalization verification of first order ship response mathematical model
由于操纵性指数T1、T2、T3较难测量,因此,20°/20° Z形试验利用式(1)解算。将MGWO算法优化后的K、T1、T2、T3代入式(2)得到二阶船舶响应型数学模型的泛化性结果。根据图5和图6可知,所提算法的预报结果与仿真试验数据相差较小,其中,一阶船舶响应型数学模型泛化性验证结果中艏向角的MAE为5.15°,二阶船舶响应型数学模型泛化性验证结果中艏向角的MAE为5.00°。另外,对于一阶船舶响应型数学模型,仿真试验的第一超越角为36.49°,预报结果的第一超越角为33.09°。对于二阶船舶响应型数学模型,预报结果的第一超越角为33.96°,预报结果与仿真试验结果误差相对较小。
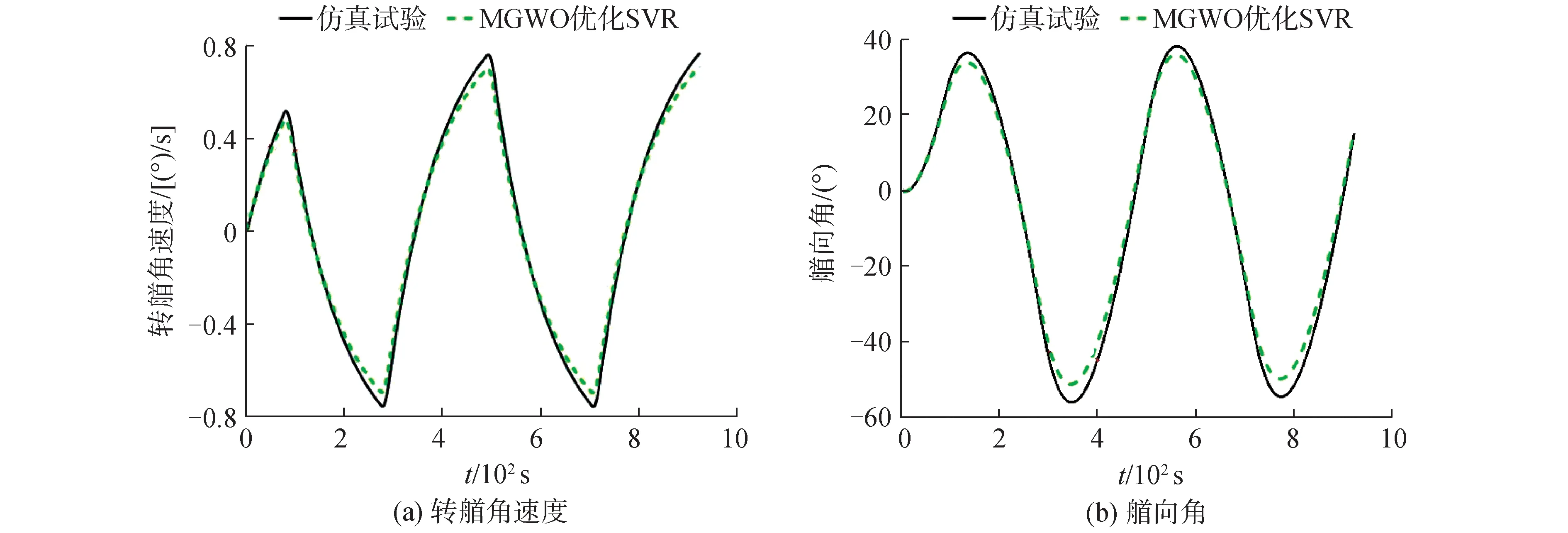
图6 二阶船舶响应型数学模型泛化性预报结果Fig.6 The generalization verification of second order ship response mathematical model
当SVR辨识效果较差时,可以利用MGWO算法对其得到的参数辨识结果进行范围内优化以得到更好的预报效果。同时,实验结果也表明了MGWO算法是一种高效的寻优算法,在有大致的参考值情况下,可以为船舶响应型数学模型寻找到贴近于理论值的操纵性指数。
4 结论
1)当参考值不准确时,利用MGWO算法对参考值进行范围内寻优以得到较好的预报结果。
2)对GWO算法进行改进以提高算法的全局搜索能力并采用单峰、多峰基准函数作为算法搜索性能测试。最终的测试结果验证了MGWO算法的搜索性能。
3)SVR是一种有效的辨识建模方案。但在二阶响应型数学模型参数辨识中,SVR的辨识效率下降,利用MGWO算法对SVR辨识结果优化。优化后的操纵性指数与理论值偏差较小。
