考虑时序数据缺失的配电网线损率动态预测方法

马晓琴，薛峪峰，杨 媛

（1.国网青海省电力公司信息通信公司，青海西宁 810008；2.国网青海省电力公司海东供电公司，青海海东 810600）

线损率是指线损与供电功率之比，其是反映电网规划设计和运行管理水平的一个重要经济指标，直接影响着配电系统的日常维护工作。线损率的预测受设备异常采集、负载转移、双用户供电切换等多种因素的影响，使得少数统计结果与实际数据不符。对线损率预测结果与实测结果进行对比，可以有效地检验配电网的数据量测与网络拓扑的联系是否正确、可靠。以往提出的基于最小二乘支持向量机的预测方法，利用离散粒子群优化算法，从配电网络的运行数据中查找含有大量运行状况的样本，并建立了一个专家样本库。利用最小二乘算法，构建线损率预测模型[1]。提出的基于深度学习的线损率预测方法，在综合考虑主、客观两个方面的因素的基础上，计算配电网线路参数权重，采用加权方法，构建预测模型，将各种配电网线路参数输入该模型中，并对其分析，获取预测结果[2]。由于预测过程中出现了时序数据缺失问题，上述两种预测方法难以用于动态线损预测情况，为此，提出了考虑时序数据缺失的配电网线损率动态预测方法。

1 基于改进KNN的缺失时序数据补全算法

文中提出了一种新的基于改进KNN 的缺失时序数据补全方法，对数据丢失的问题进行了处理，图1 显示了该过程。

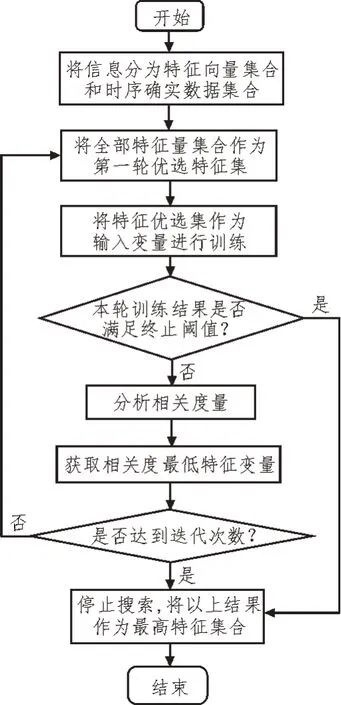
图1 基于改进KNN的缺失时序数据补全流程设计

由图1 可知，设计的详细补全步骤如下所示：

步骤1 弗雷歇距离计算：假设XC集合由x集合和x* 集合组成，其中，x集合是由n维空间的(a1(x),a2(x),…,an(x))特征向量组成的，x*集合是由时序数据缺失样本组成的[3-4]。计算x*在XC集合中与x的弗雷歇距离，该距离是一种解决空间路径相似度的方法，能够精准判别曲线相似度，其原理如图2所示。

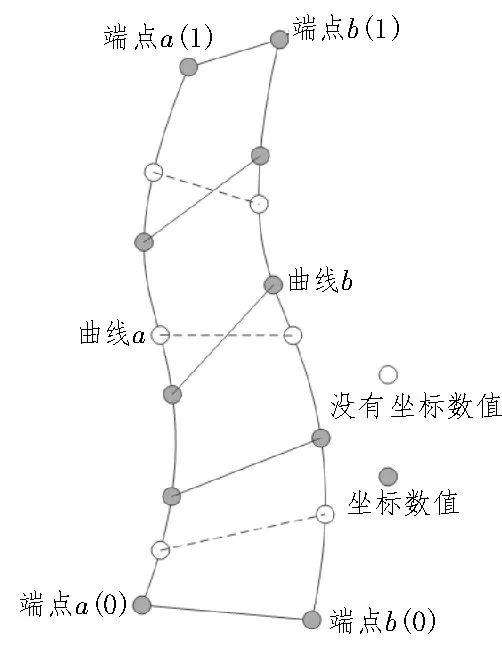
图2 弗雷歇距离计算示意图

图2 中的曲线a代表x集合，曲线b代表x*集合，两个集合的弗雷歇距离计算公式为：

式中，d表示度量函数；t为时序变量；α、β表示作用于两个曲线的重参数化函数[5-6]。

在计算结果中只考虑x*集合中没有坐标的数值，根据该数值确定x*集合中的k个最近邻，进而插补缺失坐标值[7]。

步骤2 基于改进KNN 的嵌入式特征选择：对输入时序特征变量和历史数据进行相关性分析，通过后向搜索方法获取最优特征集合。对每个特征变量及预期变量进行分析，在第一个分析过程中，所有的特征参数都被用作函数候选集[8-9]。在每次分析过程中，将最少的相关变量剔除，直到达到临界点为止[10]。其中，具有最大负载预测准确率的特征集合被确定为最后的优先特征集。

步骤3 基于改进KNN 的数据补全：通过时序集合，使用改进KNN 进行有监督学习，基于此，构建一种新的门控循环模型[11]，包括更新门和重置门，其中更新门负责控制前一时序的状态信息保留程度，重置门负责确定是否结合当前信息[12]。不断重复学习过程，使原始时序数据通过学习后获取一种包含缺失数据的序列，能够更好地学习到x集合和x*集合的时序关系。

2 基于马尔科夫模型的线损率动态预测

利用马尔可夫模型进行预测，并进行相关误差的估算。通过对状态区间的分割，求得状态转换概率矩阵，通过修正理论损失率的预测误差，使得计算结果与实际情况更加吻合[13]。详细步骤为：

步骤1 数据预处理：首先，通过对采样数据的预处理，将其转化为[-1,1]区间内。

步骤2 马尔可夫预测模型的建立：马尔可夫结构层在输入层、隐层和输出层中加入了承接层，其特征类似于BP 等前向网络，能够实现反馈式连接[14]。隐层的结点数目和承接层的节点数目一一对应，由于承接层具有反馈与记忆的作用，使得马尔可夫模型具有更高的灵敏度和较强的动态信息处理能力，以实现动态模型构建的目标。

马尔可夫预测模型是一种基于概率随机预测的模型[15]，根据预测值的大小，将其划分为下列类型m状态，然后根据相应的区间将数据放置到模型中，得到的考虑时序数据缺失的第n步状态转移概率矩阵f(m)为：

根据式（2）可确定状态转移概率矩阵，并求出最佳的数据区间。

步骤3 预测结果：采用优化的最优网络模型，对线损率进行了预测，并将其回归到实际区间，从而得出了其理论线损率的预报结果。

步骤4 判断线损率波动趋势：若想判断线损率的变化趋势，必须对影响线损率变动的各种因素进行分析，其中包括售电量结构影响因子、专线管理水平影响因子及公用线管理水平影响因子。

①售电量结构影响因子：售电量是指由供电公司销售的电量，其中包括直接销售给客户的电能和销售到其他电力公司的电能，以及用于非电力生产的电能。

②专线管理水平影响因子：高压配电网被供给到特殊的变压器，而低压配电网则是通过特殊的变压器来输出。随着电力消耗的增加，专用线路的损失也随之增加。

③公用线管理水平影响因子：公用线路是接地或母线和零线，在电力系统中，电力损耗的完整性直接关系到电力系统的运行效率[16]。

步骤5 基于动态潮流的线损率计算：按照配电网实际运行情况，计算售电量结构影响因子、专线管理水平影响因子、公用线管理水平影响因子影响下的损耗，公式为：

式中，λz表示售电量所占比重；pz表示专线线损率；pg表示公用线线损率。为了更精准反映各个因子随时间变化情况，经过累加得到的动态潮流线损率为：

式中，W表示供电量。

线损率是指配电网络中输电线损失的百分比，该指标是衡量企业运营、管理和规划设计水平的重要指标。所以，线损率计算结果既能体现配电网的结构和运行模式，又能体现供电企业的技术管理水平。经过累加计算的动态潮流线损率，使预测结果更加精准。根据营销普查的业务需要，对营销稽查、计量设备业主等重点工作开展档案异常信息查询、营销普查计划管理、营销普查工作管理。

3 实验

3.1 实验数据来源

实验数据采集的时间跨度为2020 年5 月1 日到9 月1 日，实验采集配电网正常工作时的电力运行数据，将每天24 h 采集的数值作为当天样本记录，进而实现所有参数的采样频率一致。对采样数据进行清洗与预处理，包含缺失的数据，根据先验知识，避免对预测结果造成影响。采集到的10 条配电线路的参数如表1 所示。

表1 实验参数统计结果

将统计的参数划分为三个数据子集，A 组用于训练，B 组用于误差分析，C 组用于检验。使用Matlab 工具对考虑时序数据缺失的配电网线损率动态预测方法进行验证分析。

3.2 实验结果与分析

在考虑专线管理水平影响因子、公用线管理水平影响因子不变的情况下，对比最小二乘SVM 预测方法（方法1）、基于深度学习的预测方法（方法2）和考虑时序数据缺失的预测方法（方法3）受到售电量结构因子影响下的预测结果，如图3 所示。

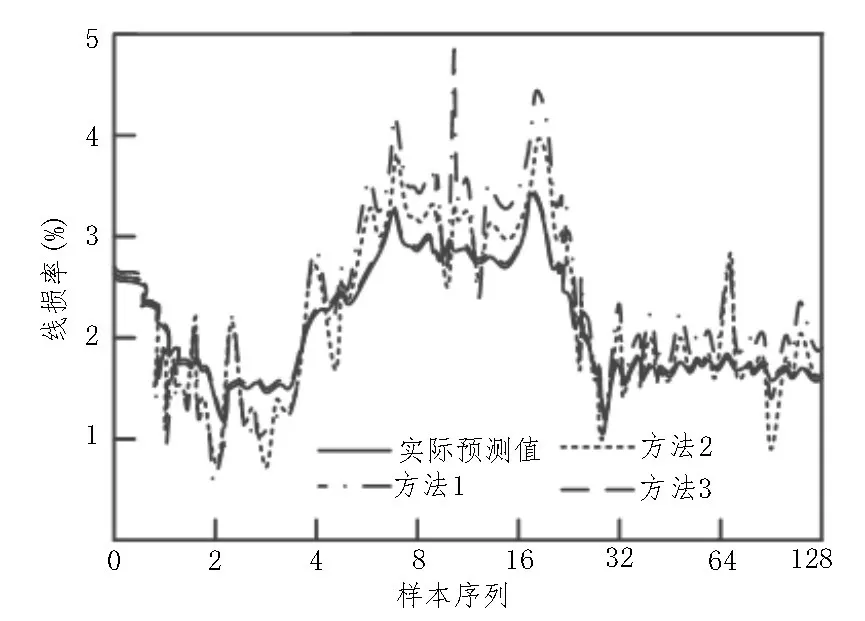
图3 售电量结构因子影响下预测结果

由图3 可知，使用方法1 与实际预测结果相差较大，在样本序列为11 时，线损率与实际预测结果相差最大，误差为3.05%；使用方法2 与实际预测结果相差较大，其中在样本序列为18 时，线损率与实际预测结果相差最大，误差为0.45%；使用方法3 与实际预测结果基本一致，仅存在0.02%的误差。

在考虑售电量结构影响因子、公用线管理水平影响因子不变的情况下，对比三种方法受到专线管理水平因子影响下的预测结果，如图4 所示。

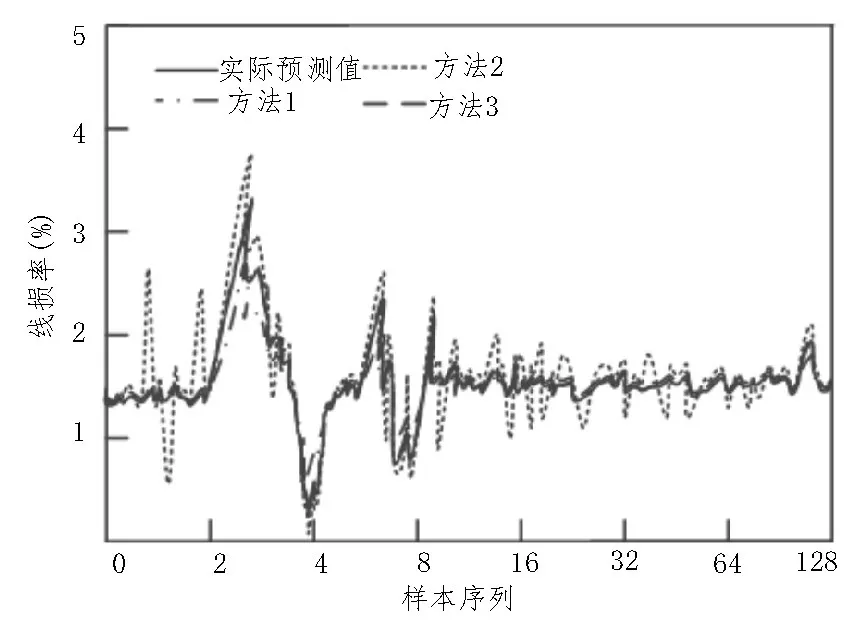
图4 专线管理水平因子影响下预测结果

由图4 可知，使用方法1 与实际预测结果最大误差为1.1%；使用方法2 与实际预测结果最大误差为2.65%；使用方法3 与实际预测结果基本一致，仅存在0.01%的误差。

在考虑售电量结构影响因子、专线管理水平影响因子不变的情况下，三种方法受到公用线管理水平因子影响下的预测结果，如图5 所示。

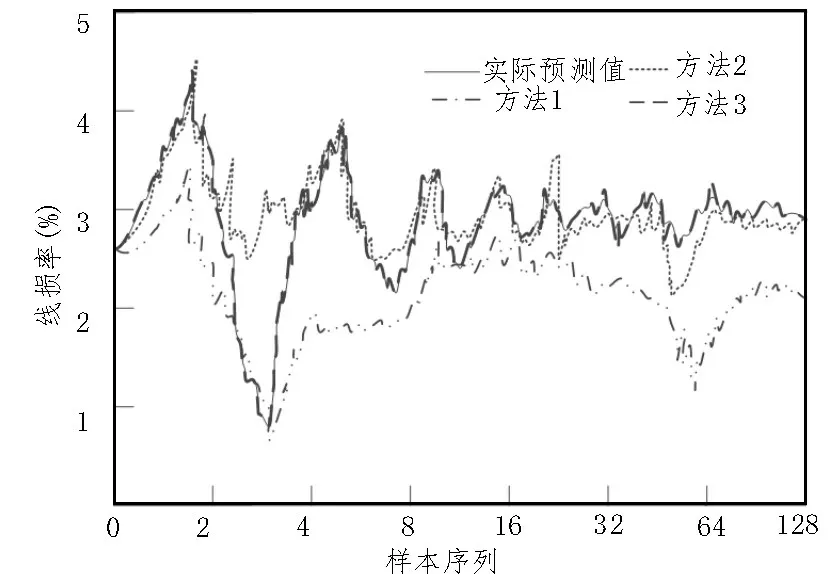
图5 公用线管理水平因子影响下预测结果

由图5 可知，使用方法1 与实际预测曲线相差较大，最大误差为2.1%；使用方法2 与实际预测结果最大误差为1.8%；使用方法3 与实际预测结果存在0.2%的误差。通过上述分析结果可知，使用考虑时序数据缺失的预测方法能够精准预测配电网线损率。

4 结束语

提出的考虑时序数据缺失的配电网线损率动态预测方法，利用基于改进KNN 的缺失时序数据补全算法补全缺失数据，结合马尔科夫模型，预测配电网线损率。通过实验验证结果发现，该方法线损率预测精准度较高。通过对客户基础数据、电价执行、电费抄收、计量管理、市场能效等方面的调查，发现管理上的缺陷和不足，进一步夯实市场基础，加强营销基础档案的质量。