高水压隧道盾构管片不同拼装方式力学性能分析
2023-08-26彭科峰周书剑李树忱刘修义唐苑寿
彭科峰 周书剑 李树忱 刘修义 唐苑寿

摘要:
水下隧道修建时,盾构管片承受着巨大水土压力,设计施工面临着重大技术难题。为此,针对江苏江阴长江水下隧道最大水压断面,分别使用修正惯用法与梁-弹簧法建立管片衬砌模型,通过调整封顶块位置与错缝角度研究了高水压下不同拼装方式对管片力学性能的影响。结果表明:修正惯用法计算结果变化平滑,而梁-弹簧法计算结果分布趋势则受接头影响,在接头位置会产生较大突变;管片力学性能受封顶块位置与错缝角度影响较大,随着错缝角度的增加,管片最大轴力、最大弯矩与最大位移以标准块圆心角度数为周期,呈周期性变化。施工过程中,为了防止产生较大位移,应尽量避免前后环管片接缝重合。研究结果可为高水压盾构隧道管片的拼装方式设计提供参考。
关 键 词:
高水压; 盾构管片; 梁-弹簧法; 修正惯用法; 力学性能
中图法分类号: TU311
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2023.08.023
0 引 言
近年来,盾构法凭借着自动化程度高、人力少、安全等特点[1],在城市隧道工程建设中大量应用[2]。越江隧道修建时,盾构管片承受着巨大的水土压力,设计施工上面临着重大技术难题。管片拼装方式设计是高水压盾构隧道设计的重要组成部分,影响着盾构管片力学性能[3],对管片结构安全有着不可忽视的重要作用[4]。
惯用法、修正惯用法与梁-弹簧法是工程上常用的3种管片计算方法。惯用法认为装配式衬砌组成的圆环可以近似看成是一个均质刚性圆环,不用考虑管片接头引起的刚度降低。修正惯用法引入了弯曲刚度有效率η与弯矩增减系数ξ来弥补管片连接造成的刚度损失[5]。梁-弹簧法用梁单元来模拟管片,用回转弹簧与剪切弹簧来模拟管片间接头与环间接头[6]。修正惯用法计算方便,建模简单,但是其将整个模型视为一个均质圆环,并不能准确模拟管片连接的情况[7]。梁-弹簧法更接近工程实际,常用来研究管片在不同拼装方式下的力学性能[8]。近年来,一些学者通过理论、试验及数值方法对不同拼装方式下管片力学性能做了大量分析。朱伟[9]、朱合华[10]等分别提出了壳-弹簧模型与梁-接头模型来模拟错缝拼装时螺栓的连接作用。何川等[11]为研究通缝、错缝拼装方式下管片应力的分布规律,开展了结构原型试验,并对管片表面应力进行了分析。葛世平等[12]对管片接头刚度进行了修正,并通过室内足尺试验进行了验证。王士民等[13]开展了封顶块位于不同位置的相似模型试验,从而研究封顶块不同位置对管片的受力与刚度的作用机理。封坤等[14]探讨了盾构隧道管片拼装效应产生机理,并研究了纵向力作用对管片环向内力的作用机制。梁坤等[15]为了探明封顶块位置对高水压盾构隧道管片结构的受力影响,开展了通缝模型试验。
以上研究主要集中在通缝与错缝力学性能的比较上,针对封顶块位置与不同错缝角度对管片结构力学性能的影响研究较少。为此,本文针对位于江苏江阴的长江水下隧道最大水压断面,使用修正惯用法与梁-弹簧法建立管片衬砌模型,通过调整封顶块位置与错缝角度研究高水压下不同拼装方式对管片力学性能的影响。
1 工程背景
1.1 工程地质
该水下隧道为长距离、大直径、高水压和大埋深水下盾构隧道。隧道总长度超过6 000 m,水下段长度为4 947 m。水下段经过地层主要为粉质黏土层与粉细砂层,局部穿越淤泥质软弱土层。该盾构隧道工程场区覆盖层包括全新统人工填土(Q4ml)、冲洪积层(Q4al+pl)与下更新统冲洪积层(Q1al+pl);隧道外直径超过15 m,承受最高水压超过60 m,最大覆土深度超过40 m,管片设计施工上面临着重大技术难题与风险挑战。地层参数如表1所列。
1.2 盾构管片
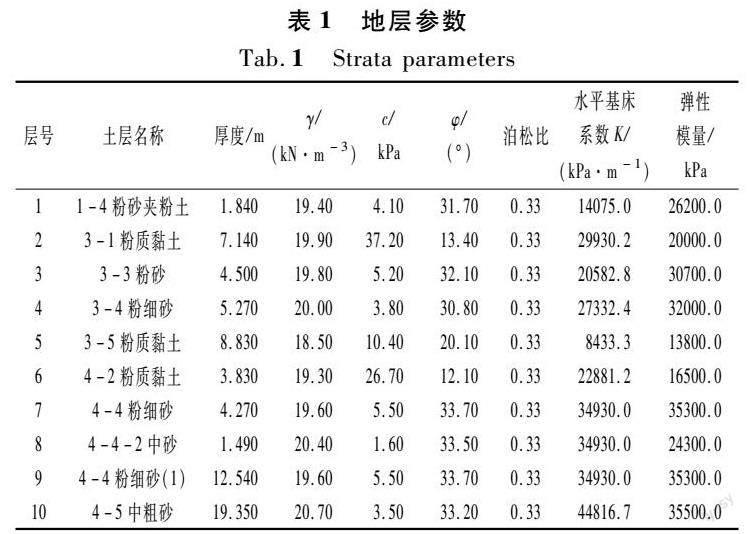
水下隧道盾构管片外径为15.5 m,内径为14.2 m,宽度为2 m。衬砌环采用C60混凝土浇筑而成,由1块封顶块,2块邻接块与7块标准块共10块管片通过环向接头连接而成。在管片中间,即距圆心14.85 m处设置56个纵向接头用以连接衬砌环。管片构造如图1所示,因为邻接块与标准块圆心角角度十分接近,为简化后续计算,在梁-弹簧法计算过程中,统一视为标准块。封顶块圆心角为12.86°,标准块圆心角为封顶块的三倍,即38.58°,由于模型简化影响,角度值与图1中略有差别。
2 最大水压断面计算
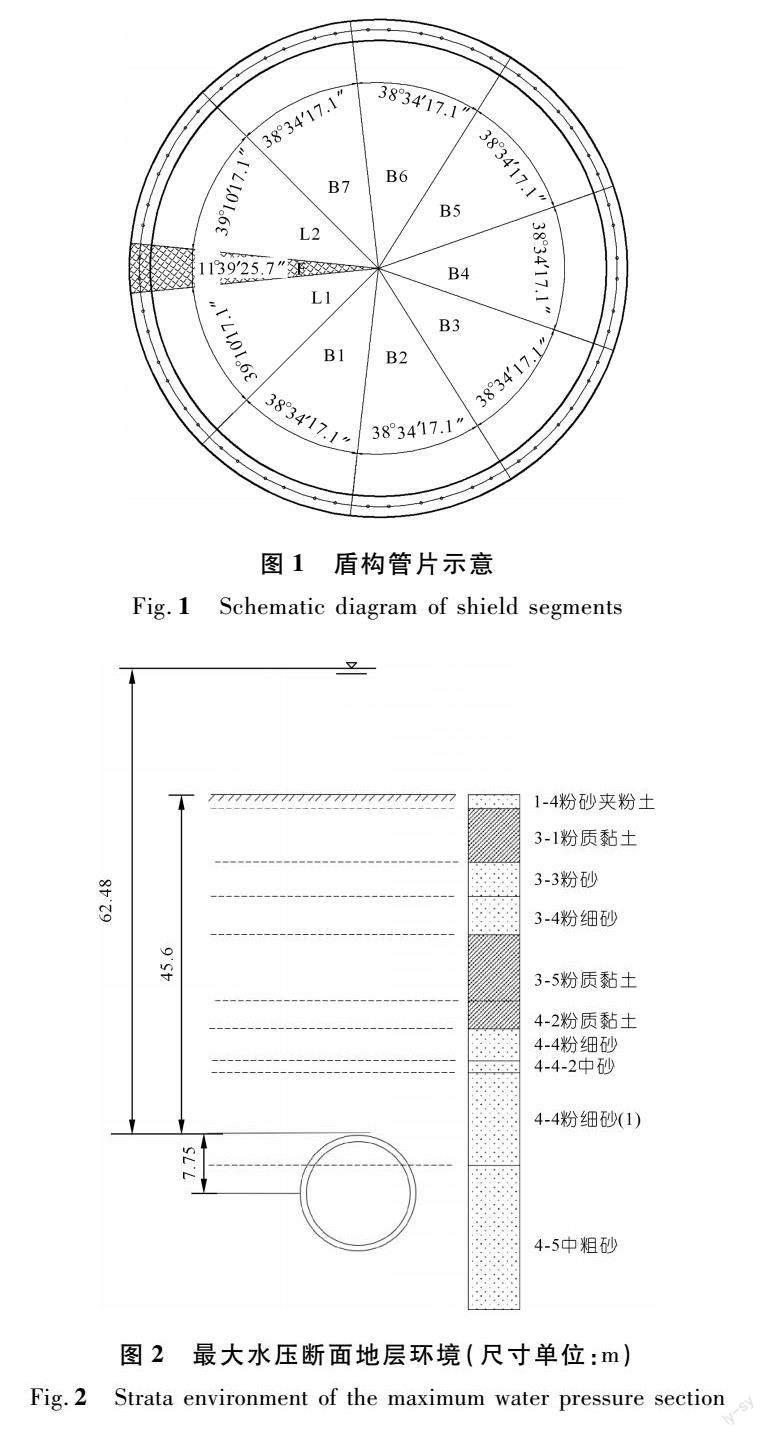
为研究高水压下不同拼装方式对管片力学性能的影响,选取隧道的最大水压断面,其断面地层环境如图2所示。衬砌管片位于粉细砂层与中粗砂层之间,距水平面62.48 m,距陆地表面45.61 m。分别采用修正惯用法与梁-弹簧法建立管片衬砌模型,研究管片的力学性能,并对所得结果进行比较。
2.1 外荷载计算
如图3所示,通过荷载结构法,将隧道管片所受竖向外荷载分为土荷载Pe1与水荷载Pw1,并分别进行计算。当管片覆土深度大于管片外直径时,衬砌管片所受土荷载可近似看成是松弛土压力[16],并将隧道外径的2倍作为所受土荷载的最低有效高度。
采用Terzaghi公式计算隧道所受土荷载:
B1=D02·cotπ/4+φ/22(1)
h0=B11-c/B1γK0tanφ1-e-K0tanφHB0+P0γe-K0tanφHB0(2)
式中:B1为松弛宽度,m;φ为土体的内摩擦角,(°);h0为有效高度,m;c为土体的黏聚力,Pa;K0土体水平土压力与竖直土压力之比,文中取1;γ为土体重度,N/m3;γ′为土体浮重度,N/m3;P0为上部荷载,Pa;D0为管片的外径,m。
最大水压力断面处,衬砌的外径D0=15.5 m,内摩擦角φ=33.7°,土体重度γ=19.60 kN/m3,浮重度γ′=9.60 kN/m3,黏聚力c=5.5 kPa,上部荷載P0=20 kPa。代入式(1)、(2),求得有效高度h0=18.39 m,小于管片外径的两倍,则有效高度h0=2D=31 m,管片所受覆土荷载Pe1=γ′h0=19.6×31=297.60 kN。
管片结构距水平面62.48 m,管片所受水荷载Pw1=γwh=10×62.48=624.80 kN,其他荷载计算结果如表2所列。
2.2 地层弹簧刚度
由Winkler假设,地表上沉降变形与承受的地层压力成正比,因此可以将地层简化为一系列彼此不关联的弹簧。选取ANSYS平台combin39单元模拟地层的抗力作用,并设置受压时地层弹簧刚度KRi与受拉时弹簧刚度Kci。弹簧单元长度设置为1 m,抗压时地层弹簧刚度KRi由式(3)得出:
KRi=Ki·Ai(3)
式中:KRi为受压时地层弹簧刚度,kN/m;Ki为地层抗力系数,kN/m3;Ai为每个地层弹簧对衬砌管片的接触面积,m2。本文设置弹簧接触面积为0.416 5 m2,地层抗力系数4 000 kN/m3,代入式(3),求得受压时地层弹簧刚度为1 666 kN/m,考虑到围岩不抗拉的特性,受拉时弹簧刚度Kci设置为0。
2.3 修正惯用法计算
取单环管片进行计算,管片参数如表2所列,管片外荷载根据表3选取。
在ANSYS平台上使用beam188单元建立单环衬砌管片,并施加管片外荷载与地层弹簧,建立修正惯用法模型,如图4所示。图5为修正惯用法计算结果。由图5(a)轴力计算结果可知,管片轴力为左右对称分布,在12 900~14 400 kN范围内变化,变化幅度较小。如图5(b)所示,管片最大负弯矩出现在拱顶位置,为982.72 kN·m。考虑到弯矩增减系数ξ,管片截面弯矩为(1+ζ)M=1 277.54 kN·m,管片接头弯矩为(1-ζ)M=687.90 kN·m。管片的最大正弯矩发生在拱肩位置,为617.91 kN·m,管片截面弯矩为803.28 kN·m,管片接头弯矩为432.53 kN·m。管片出现椭圆状变形,最大竖向位移出现在拱顶位置,为12.47 mm;最大横向位移出现在拱腰位置,为3.91 mm。
2.4 梁-弹簧法计算
图6为梁-弹簧法所建模型示意图,模拟过程中,令A环,C环封顶块位置保持不变,通过旋转B环来模拟错缝拼装,使用接缝回转弹簧K1来模拟单环管片中块体之间接头,使用径向剪切弹簧K2与切向剪切弹簧K3来模拟衬砌管片环间接头。
选取中间环管片,即B环进行分析,管片的轴力、弯矩与位移如图8所示。管片轴力为对称分布,在12 900~14 900 kN范围内变化,并在拱腰处取得最大值,拱顶处取得最小值。弯矩分布结果则受管片接头影响,存在较大突变,最大负弯矩发生在封顶块两端接头处,为1 560 kN·m;最大正弯矩发生在左侧拱肩位置,为964.45 kN·m。最大竖向位移发生在拱顶位置,为12.38 mm;最大横向位移发生在拱腰位置,为3.90 mm。
2.5 不同计算方法结果对比
将修正惯用法与梁-弹簧法所建模型弯矩值与轴力值进行对比,绘制分布曲线,结果如图9、10所示。
修正惯用法与梁-弹簧法所得计算结果都可近似看成是对称分布,但修正惯用法计算结果变化平滑,而梁-弹簧法计算结果则受接头影响,在接头位置会产生较大突变,符合工程实际。相比于梁-弹簧法,修正惯用法虽然在一定程度上考虑了因管片接头造成的刚度损失,但在精细化模拟管片接头性能方面仍不如梁-弹簧法。
3 管片不同拼装方式性能研究
为探究管片不同拼装方式对管片性能的影响,使用上节所述梁-弹簧法构建三環管片模型。令前后环封顶块分别处于拱顶、拱肩与拱腰位置,中间环管片进行顺时针旋转,每次旋转12.86°,共旋转14次,总计42个工况。对各个工况管片的最大轴力,最大弯矩与最大位移进行比较分析。
3.1 最大轴力
管片最大轴力计算结果随错缝角度变化如图11所示,可知,管片最大轴力随错缝角度的增加在14 500~15 500 kN范围内以38.58°为一个周期,呈现周期性变化。最大轴力整体变化幅度较小,最大值与最小值差距仅为6.89%。当封顶块位于拱肩处,且错缝角度为0°时,最大轴力取得最小值;当封顶块位于拱肩处,错缝角度为64.28°时,最大轴力取得最大值,为15 500 kN。
3.2 最大弯矩
管片最大正弯矩与最大负弯矩计算结果随错缝角度变化如图12,13所示。其中,管片最大正弯矩变化范围为516.03~933.97 kN·m,整体变化幅度较大。当封顶块位于拱顶位置处,错缝角度为0°时,管片最大正弯矩取得最小值。当错缝角度为115.71°时,管片最大正弯矩取得最大值。最大负弯矩变化范围为584.13~1 670.12 kN·m,当封顶块位于拱顶处且错缝角度为0°时,最大负弯矩取得最小值;当封顶块位于拱腰处且错缝角度为12.86°时,最大负弯矩取得最大值。
管片最大正弯矩与最大负弯矩以38.58°为一个周期,呈现周期性变化。当封顶块位于拱顶位置处,随着错缝角度的增加,管片最大正弯矩与最大负弯矩波动较小;当封顶块位于拱肩位置处,波动较大。
通缝拼装下管片所受最大弯矩值低于错缝拼装,这是因为错缝拼装下,纵向接头的咬合作用致使管片受到前后环管片的约束,从而使管片所受弯矩增大,刚度增加。
3.3 最大位移
管片最大竖向位移与最大横向位移计算结果如图14,15所示。管片最大竖向位移受封顶块位置与错缝角度影响较大,与弯矩变化类似,以38.58° 为一个周期,呈现周期性变化。最大竖向位移在10.76~12.69 mm范围内变化,当封顶块位于拱顶位置,错缝角度为0°时,最大竖向位移取得最大值,当封顶块位于拱腰位置,错缝角度为115.71°时,取得最小值。通缝拼装下管片最大竖向位移大于错缝拼装。这与造成最大弯矩变化的原因相同,是因为纵向接头使衬砌圆环的刚度增加,从而使得管片变形减小。
管片最大横向位移受封顶块位置与错缝角度影响较小。相同错缝角度下,封顶块位置位于拱腰处的最大横向位移最大。最大横向位移在3.78~4.09 mm范围内变化,当封顶块位置位于拱顶处,错缝角度为102.86°时,最大横向位移取得最小值,当封顶块位置位于拱腰处,错缝角度为167.24°时,最大横向位移取得最大值。
封顶块位置对管片位移影响较大,相同错缝角度下,封顶块位于拱顶时的最大竖向位移大于封顶块位于拱腰与拱肩的最大竖向位移。封顶块位于拱腰时的最大横向位移大于封顶块位于拱顶与拱肩的最大横向位移。
3.4 结果分析
封顶块位置对于管片力学性能有较大影响,当封顶块位于拱顶位置时,管片轴力值与弯矩值随错缝角度波动较小,相同错缝角度下,封顶块位于拱顶时的最大竖向位移大于封顶块位于拱腰与拱肩的最大竖向位移。封顶块位于拱腰时的最大横向位移大于封顶块位于拱顶与拱肩的最大横向位移。
管片结构最大弯矩、最大轴力与最大位移受错缝角度影响较大。随着错缝角度的增加,管片最大弯矩、最大轴力与最大位移以错缝角度以38.58°为一个周期呈现周期性变化。这是因为38.58°是标准块圆心角度数,当管片错缝角度为标准块度数或标准块圆心角度数的倍数时,中间环封顶块与标准块的接缝会与前后两环标准块与标准块的接缝重合,从而降低了纵向接头的咬合作用,减小了管片的刚度,弯矩、轴力随之减小,位移随之增大;当中间环继续顺时针旋转时,不再产生接缝重合,弯矩、轴力逐渐增大,位移逐渐减小。
4 结 论
本文依托江阴长江水下隧道工程,分别使用修正惯用法与梁-弹簧法模拟最大水压断面的管片结构,通过调整封顶块位置与错缝角度对高水压下不同拼装方式管片的力学性能进行分析,得到了以下结论:
(1) 修正惯用法与梁-弹簧法均可以较好模拟管片力学性能,计算结果大体相同。但梁-弹簧法可以准确模拟管片接头处的力学性能,与实际更相符,因此推荐使用梁-弹簧法对管片受力性能进行研究。
(2) 封顶块位置对于管片力学性能有较大影响。当封顶块位于拱顶位置时,管片轴力值与弯矩值随错缝角度波动最小。相同错缝角度下,封顶块位于拱顶时的最大竖向位移最大,位于拱腰時的最大横向位移最大。
(3) 随着错缝角度的增加,管片结构最大弯矩、最大轴力与最大位移以标准块圆心角度数为周期呈现周期性变化。错缝拼装时,为了防止产生较大位移,应尽量避免前后环管片接缝重合。
参考文献:
[1] 闫鑫,姜厚停,龚秋明.土压平衡盾构施工中泡沫改良砂土的试验研究[J].地下空间与工程学报,2010,6(3):449-453.
[2] 何川,封坤.大型水下盾构隧道结构研究现状与展望[J].西南交通大学学报,2011,46(1):1-11.
[3] NO W G,ASSOCIATION I T.Guidelines for the design of shield of tunnel lining[J].Tunnelling and Underground Space Technology,2000,15(3):303-331.
[4] 姚广亮,陈震,严振瑞,等.高内水压盾构隧洞预应力混凝土内衬结构受力分析[J].人民长江,2020,51(6):148-153.
[5] 孙波,傅鹤林,张加兵.基于修正惯用法的水下盾构管片的内力分析[J].铁道科学与工程学报,2016,13(5):929-937.
[6] 朱合华,周龙,朱建文.管片衬砌梁-弹簧广义模型及接头转动非线性模拟[J].岩土工程学报,2019,41(9):1581-1590.
[7] 陈炜韬,傅支黔,马建新.大直径双护盾TBM隧道管片厚度设计研究[J].铁道建筑,2017,57(10):60-62.
[8] 张建刚,李围,何川.基于内置接头参数数组的整环衬砌模型结构分析[J].人民长江,2020,51(4):152-156.
[9] 朱伟,黄正荣,梁精华.盾构衬砌管片的壳-弹簧设计模型研究[J].岩土工程学报,2006,28(8):940-947.
[10] 朱合华,崔茂玉,杨金松.盾构衬砌管片的设计模型与荷载分布的研究[J].岩土工程学报,2000,22(2):190-194.
[11] 何川,封坤,杨雄.南京长江隧道超大断面管片衬砌结构体的相似模型试验研究[J].岩石力学与工程学报,2007,26(11):2260-2269.
[12] 葛世平,谢东武,丁文其,等.盾构管片接头简化数值模拟方法[J].岩土工程学报,2013,35(9):1600-1605.
[13] 王士民,于清洋,彭博,等.封顶块位置对盾构隧道管片结构力学特征与破坏形态的影响分析[J].土木工程学报,2016,49(6):123-132.
[14] 封坤,何川,邹育麟.大断面越江盾构隧道管片拼装方式对结构内力的影响效应研究[J].工程力学,2012,29(6):114-124.
[15] 梁坤,封坤,肖树,等.封顶块位置对高水压通缝拼装管片结构的影响[J].西南交通大学学报,2020,55(6):1231-1239.
[16] 日本土木学会.隧道标准规范(盾构篇)及解说[M].北京:中国建筑工业出版社,2001.
[17] 张厚美,过迟,付德明.圆形隧道装配式衬砌接头刚度模型研究[J].岩土工程学报,2000,22(3):309-313.
(编辑:郑 毅)
Abstract:
During the construction of cross-river tunnels,the shield segments are under enormous water and soil pressure,and the design and construction are facing with major technical problems.In view of the maximum water pressure section of an underwater tunnel in Jiangyin reach of Changjiang River,a segment lining model was established by using the modified usage method and the beam-spring method respectively.The influence of different assembly methods on the mechanical properties of the segments under high water pressure is studied by adjusting the position of the capping block and the staggered joint angle.The results show that the calculation results of the modified usage method change smoothly,while the distribution trend of the beam-spring method calculation results is affected by the joints,and there is a sudden change around the position of the joints.The mechanical properties of the segment are greatly affected by the position of the capping block and the staggered joint angle.With the increasing of the staggered joint angle,the maximum axial force,bending moment and displacement of the segment change periodically with the central angle of the standard block as a period.During the construction,in order to prevent large displacement,it is necessary to avoid the overlap of the front and rear ring segment joints.The above results can provide a reference for the design of segment assembly in high water pressure shield tunnels.
Key words:
high water pressure;shield segments;beam-spring method;modified usage method;mechanical performance
