无人工程机械路径规划算法应用
2023-08-26杨夏宁黄位伟李志恒玉海韩
杨夏宁 黄位伟 李志恒 玉海韩

关键词:无人装载机;路径规划;AGV;土方机械;路径冲突
中图分类号:TP18 文献标识码:A
文章编号:1009-3044(2023)21-0024-04
0 引言
工程机械是体现国家高端制造水平的一个重要指标,目前我国的工程机械发展水平面临着前所未有的挑战。其中,核心技术不足,数字化和智能化发展落后是主要的原因。融入现代化信息技术,使机械设备向着更高端的自动化、智能化系统发展,推进“5G + 工程机械”模式[1]的发展是目前研究的重点之一。
近年来随着物流技术的发展、5G通信技术的成熟和人工仓储成本的提高。以AGV(AutomatedGuided Vehicle,AGV) 自动物料转运小车为代表的仓储自动调度和路径规划算法发展迅速,无人物流仓储通过装备分拣系统,极大地提高了现代物流的效率,进一步提高了自动化和智能化程度。AGV无人仓储作业的成功带动了各行业中无人作业的发展,相关技术的应用也不再局限于物流行业[2-3]。AGV路径规划问题一般分为全局路径规划和局部路径规划两步。全局路径规划从全局出发,不考虑动态变化规划出符合全局的最优路径;后者则实时地更新自身运行状态,实现动态地避障功能。目前常用的全局规划算法主要是A*算法[4]、粒子群算法[5]和蚁群算法[6]。局部规划常用的算法有动态窗口法[7]和人工视场法[8]。路径规划一般以路径距离代价作为主要的代价函数,计算得到的路径虽然是最短的,但是并不一定是最优的。
工程机械行业作业环境和自身运行状态复杂,对路径规划的影响都很大。单纯的以路径距离代价作为总代价函数无法满足复杂的工程问题。为了改善规划算法在工程机械及相关领域的应用,本文结合全局规划和局部规划算法,对固定作业场景的装载机倒料场景进行栅格化和拓扑化,采取A*算法寻找最短路径,并通过CBS(Conflict Based Search, CBS)算法[9]解决路径冲突问题,从而找到全局最优路径,并基于路径距离代价,考虑装载机满载和空载运行代价,面向不同的工况进行仿真实验,以提高算法的鲁棒性。
1 问题描述
为具象化算法的应用效果,本文将路径规划算法应用到实际的装载机装卸料固定作业场景中。结合实际生产需要和装载机运行条件对场景进行建模,分析算法的可行性。
1.1 场景描述
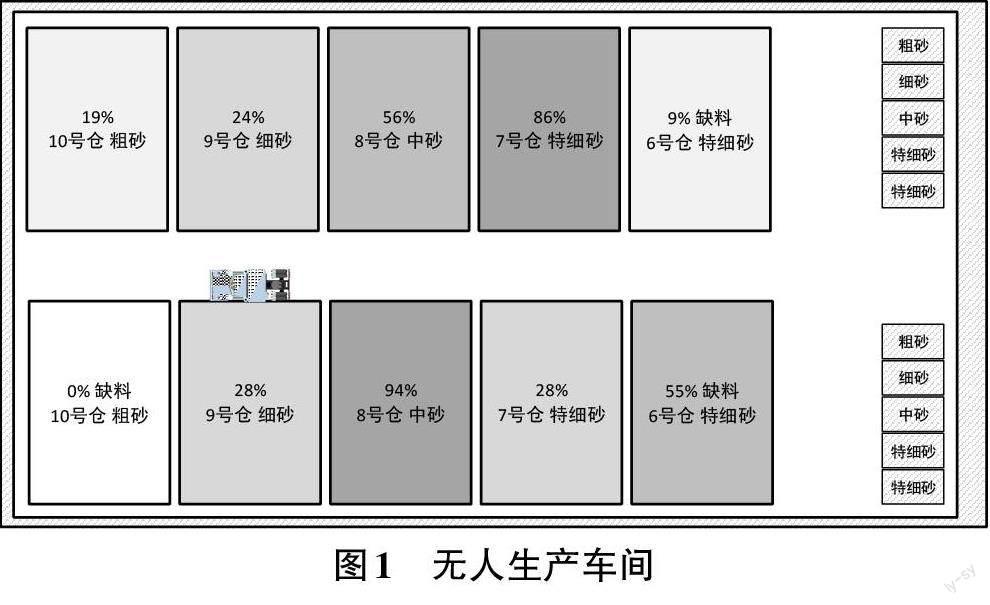
无人装载机装卸料任务在10个料仓和10个漏斗之间完成。由于场地空间的限制和对安全的考虑,装载机在作业现场行驶的过程中不允许并行,所有的道路都是单行道,图1是无人生产车间示意图。
无人生产车间包括装载机运行通道、粗砂仓库和粗砂漏斗各4个、中砂仓库和中砂漏斗各2个、特细砂仓库和特细砂漏斗各4个。为了满足生产需要,装载机需要不断地从料仓中运送砂料到漏斗,如何在规定的时间内高效地完成任务是本文方法要解决的主要问题。
多车任务调度规划问题是一个复杂的问题,通常对物料转运车的分配原则主要有最短路径原则、最短工作时间原则、工作任务优先级原则和综合指标的原则[10]。考虑到装载机造价昂贵,且作业现场空间受限,安全代价大。本文通过采用双车模型对路径规划问题进行求解,并对无人生产车间做出以下约束:
1) 通过严格限制作业场景动态信息,将作业场景固定,场景信息已知。装载机可行走的道路固定不变,车辆路径都为单行道。
2) 装载机在漏斗和料仓的作业时间固定为t ∈ (t1,t2),时间参数由装载机性能参数决定。
3) 两台装载机的型号、速度等运行参数完全一致。
由于大型机械满载和空载期间的运行状态差异较大,场景描述除了对场景做出限制,车辆自身状态的约束也是重要的举措,尽可能地减少作业场景的动态信息是保证生产稳定的一个前提。
1.2 场景建模
将实际作业空间转换为模型地图是算法研究的第一步。目前常见的地图构建方法有栅格图法、可视图法和拓扑图法。拓扑结构简洁直观,对地图进行全局规划的效率高。栅格地图精细化程度高,适合车端进行局部路径规划。为充分发挥二者的优势,本文在云端使用拓扑地图进行全局规划,并结合车端栅格地圖进行局部规划,最大限度保证路径规划的准确性和稳定性。
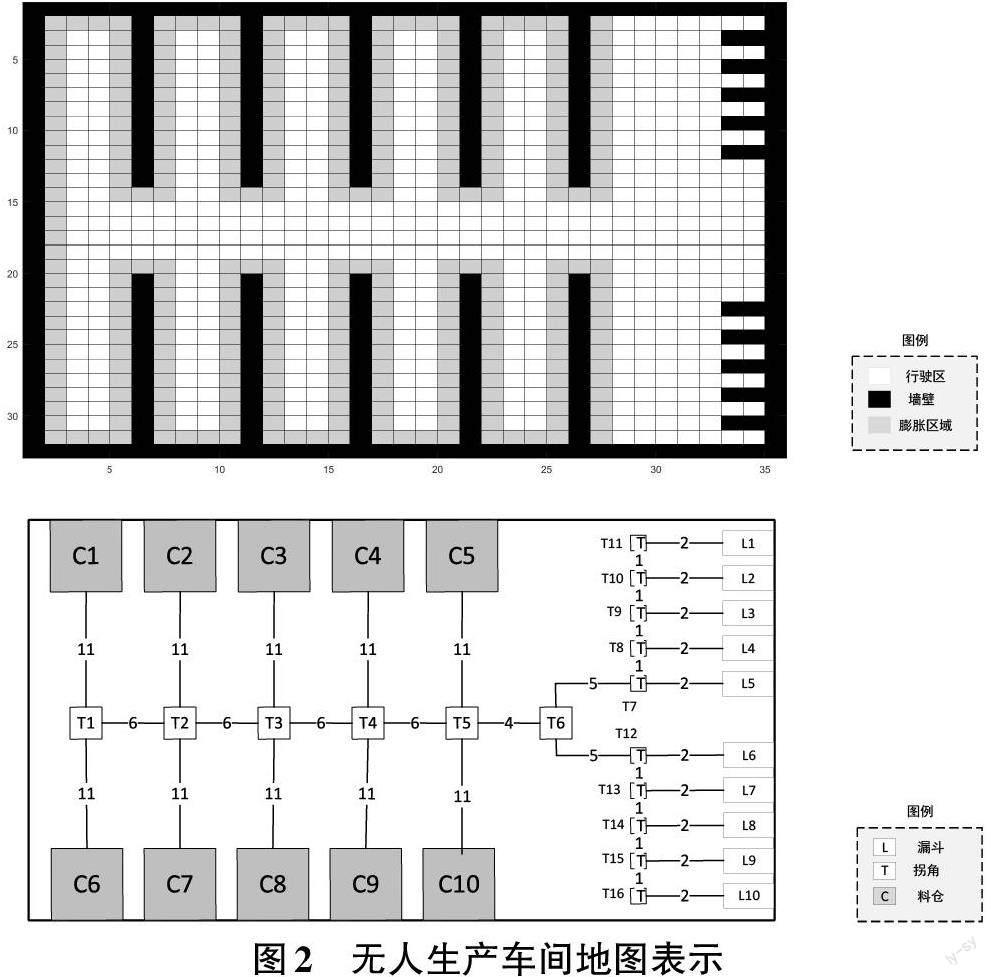
栅格图法将实际三维地图二维化,使用整齐排列的栅格来代表地图中的路径和障碍物。其中1代表障碍物,不可通行由图2上中黑色栅格表示;0代表路径,可通行由图2上中白色栅格表示[11]。栅格图表示法在场景开阔或细小障碍物较多的场景时,由于自身精细化表达能力差,刻意缩小栅格大小又会极大地增加计算量。故而并不适用于繁杂的作业场景。考虑到无人装载机装卸料生产车间场景固定,作业范围比较小,同时严格控制生产区间障碍物等动态事件。使用栅格地图足够达到任务的精度,也有利于管理控制。无人生产区间使用栅格地图表示后的场景如图2 所示。为了提高作业的安全性,在栅格地图中设立了膨胀区域由图2上中灰色栅格表示,膨胀区域内的行进代价会增加,以降低路径规划撞墙的概率。
2 路径规划算法
路径规划算法的任务是从当下环境中寻找出一条无冲突,从起始点到终点路径代价最小的路径。基于1.1所描述的场景可以将路径的冲突分为顶点冲突和边界冲突。
2.1 冲突概述
2.2 CBS 算法
CBS算法是由Guni等人于2015年提出的用于解决多目标路径规划MAPF (Multi-Agent PathFinding,MAPF) 路径冲突问题的方法。CBS算法的主要思想是通过寻找一系列连续的约束来处理所有目标路径的冲突,直到找到没有冲突点的路径集合。CBS是一个双级(two-level) 搜索算法,高级搜索部分(highlevel)是一个二叉搜索树,称为冲突树CT(ConflictTree) ,树的每个节点包含了单条的路径的基本信息和约束条件。算法低级部分是在考虑新增约束的情况下,使用A*算法重新计算得到的最短路径。
CBS算法在目标数量过多,或者路径冲突密集的情况下,搜索到的路径可能陷入局部最优解,但是对于目标数较少的模型(如双目标模型)中却有着足够高的效率和性能。在本文的双装载机作业场景中,使用CBS算法是高效的。
2.2.1 CBS 高级搜索
CBS高级搜索由冲突树完成,树的每一个节点N包含了三个部分:
1) 一系列的约束(N.constrains) 。每一个约束都作用于某一路径,根节点的约束为空,子节点继承父节点的约束。
2) 局部最优路径(N.solution) 。目前的节点路径,路径需要满足所有约束。该路径计算由A?算法完成。
3) 总代价(N.cost) 到该节点为止,得到的所有路径总代价。
具体结构及冲突处理如图5所示。
首先,规定冲突树的左子树给节点1添加约束,Con 为节点约束,Cost 为路径代价,sol 为目前的路径集合,标红部分为冲突点。该二叉树有如下特点:
1) 根结点约束为空;
2) 子结点继承父节点的所有约束,并且所有路径都是在以约束为前提的情况下得到,通过低级搜索得到;
3) 一旦搜索到目标结点,该遍历即可提前结束。
总体上,需要先使用A? 算法进行低级搜索为所有的目标ai 寻找最短路径(N1.solution),并且该低级搜索继承了所有来自父节点的约束(N1.constrains)。一旦找到新的连续路径,需要重新计算这些路径的总代价(N1.cost),并且这些目标点的新路径会重新进行冲突检测。若冲突依然存在,则在该节点的基础上增加新的约束。两个新的约束分别作用于冲突的两个目标点,生成两个新的子节点N2,N3继承于N1。依次遍历直到为所有的目标寻找到无冲突的路径。
初始给定两条冲突的最短路径1:{ D2,C2,B2,A2,A3}2:{C1,B1,B2,B3,B4}。t = 2 时,两条路径在B2点发生顶点冲突。左子树为路径1添加约束Con:{1,B2,2},路径1在t = 2时不得通过B2点,新路径为1:{ D2,D3,C3,B3,A3}2:{C1,B1,B2,B3,B4}。重新计算新路径的冲突,并以相同的方式解决,最终得到两条无冲突的局部最优路径:
类似地,冲突树的右子树为路径2添加类似约束,重新计算得到新的路径集合。一般地,最终冲突树得到的多个局部最优解需要通过路径代价Cost 做进一步筛选,但若仅以距离代价为代价总和,则冲突树深度越深的节点代价会越高,故而一旦搜索到无冲突路径即可解决CBS搜索。
对于多个目标(> 2) 的路径规划,可以生成k 个子节点构成约束森林,如图6(a) 所示,节点1,2,3在t 时刻在v 处都发生了冲突。优先考虑节点1,2的冲突,处理之后再考虑加入节点3的冲突,从而将森林拆分为二叉树进行新的迭代,如图6(b) 所示。
综合以上,CBS算法高级搜索的算法流程由表1 给出。
3 仿真实验分析
为了验证CBS路径规划算法在装载机装卸料模型中的有效性,本文通过OpenCV工具库对算法进行验证分析。栅格地图用于装载机车端的局部路径规划,拓扑图用于云端全局路径规划,由此可以清晰地表示出CBS算法寻找出的路径并实现精细化控制。
3.1 路径规划冲突仿真分析
针对两种不同类型的冲突,设置一系列不同的任务以充分证明算法的有效性。任务序列如表2所示。
每一个装料任务都包括了两段距离,分别为装载机起始位置St 到料仓C 和料仓C 到漏斗L。并且起始位置到料倉阶段,装载机空载,此时行驶的代价较小。
相反的,料仓到漏斗的距离阶段,装载机满载,此时设定装载机的行驶代价为空载时候的2倍。
假设两辆装载机的起始点分别为L1和L10,并且为方便计算,装载机到达任务地点后的作业时间代价固定为11。首先由A? 算法根据任务列表寻得的最短路径如表3所示,表中所有的路径都使用图1拓扑图结构来表示。为解决路径冲突,同时使得路径的代价最小,约定空载装载机需要为满载运行的机械让步,由此使用CBS算法得到新的无冲突路径并计算其代价如表4所示。
综上实验结果,双车模型在固定的装卸料作业场景中冲突次数较少,在本文选取4个任务单次CBS计算中仅有3次冲突。同时运行过程中只要保证满载车辆运行的路径最短,则相应的任务总代价就会越小。由此证明了CBS算法在该应用场景中不仅高效简单,更有不错的稳定性。
4结论
本文针对无人装载机装卸料作业场景进行路径规划分析,提出一种符合实际生产需求的解决方案,并通过实验分析证明了在固定的作业场景中,CBS算法在路径规划中的高效性。除此之外,采用栅格地图进行路径规划的局部规划,便于精确地控制车辆运行状态;拓扑地图进行路径规划的全局规划,方便操作人员及时地调整,增强了算法的实用性。
实验证明了在局限的场景中,CBS 算法简单高效,且具有不错的稳定性。在保证装载机满载运行路径最短的情况下,可以得到规划路径的最优解。如何更精细化地考虑机械运行的其他参数,提高整个路径规划算法的鲁棒性是后续工作需要研究的内容。
