基于机器学习的出租车轨迹大数据分析研究

金建　刘春霞　刘勇

关键词：出租车轨迹；机器学习；聚类算法；数据分析

中图分类号：TP18 文献标识码：A

文章编号：1009-3044（2023）21-0063-04

1 研究背景和意义

在大数据时代，数据的影响不再局限于企业领域。除了可以创造商业价值，数据还能够为社会创造极大价值。随着通信技术的发展，交通数据的贫乏状况得到改善，变得更加丰富。然而，由于这些数据的种类繁多、数量庞大，如何从中提取有用的信息以促进决策，尤其重要。同时对于交通数据的处理和分析，在技术上也面临着巨大的挑战，数据采集效率、数据处理方式、数据模型等各种问题，都在不断地改进和完善。

在面临如此庞大的数据量下，传统的数据库技术已经难以满足计算分析的需求，于是大数据技术顺应而出。通过大数据相关技术对交通轨迹数据的处理，结合算法，来实现对居民出行的预测、出租车热点区域的判断等。一方面可以帮助城市交通管理部门更好地合理配备或调度公共交通资源，制定出更好的统筹与协调解决方案。从而有效地提高城市交通运行效率以及提升资源利用率。另一方面可以给出租车司机行驶带来引导作用，让出租车司机能更短的时间内载到乘客，避免空载造成的道路资源浪费。

2 机器学习聚类算法研究

聚类算法有多种不同的类型，包括划分法、层次法、基于密度的聚类方法和基于网格的聚类方法等。每一种都有其各自的特征，应根据不同的应用场景和数据特点来选择不同的聚类方法。

2.1 K-means 算法

K-means算法是一种常见的聚类方法，也被称为K平均值算法或K均值算法。该算法通过随机选择K 个中心来划分数据集，每个中心对应一个簇。由于簇中心的存在，每个簇中至少有一条数据，算法会计算所有数据点与各个簇中心的距离，并将每个数据点归入最近的簇中。针对每一个类簇，重新通过最近距离来计算出它的新的簇中心。如果中心没有发生变化，就结束这个过程。否则，退回到重新继续划分到距离最近所在的簇中，如此循环。在对K-means算法聚类大规模数据集时，为了避免造成死循环，一般情况下需设定最大迭代次数。该算法具有局部最优特性，并非全局最优解。此外无法计算距离的非数值数据集不能使用K-means算法来聚类。本文中对于最短距离的计算使用欧氏距离。

2.2 其他K-means 算法

K-means算法作为经典算法之一，也存在着一些缺点。例如：对于大规模的数据，K-means算法常常需要多次迭代计算才能得到局部最优解[1]，以及往往带来大量的数据通信。针对这些存在的问题，ZHAO 等人通过基于云计算平台Hadoop，提出了PKMeans算法[2]，有效地提高了传统聚类算法处理大规模数据时的性能。Liao等人提出了改进版的基于MapReduce 的并行K-means聚类算法[3]，通过减少迭代次数和加快每次迭代时的处理速度提高了算法的性能。再后来，夏提出了并行三阶段K均值算法[4]，结合了统计方法的规则和采用了多种初始化策略，优化了K-means 的距离度量和聚类初始化，较之前的K-means算法有了更高效率和可靠性。李等人基于Spark的并行化，验证了K-means II算法在准确性和时间效率上有更高的优越性[5]。

3 算法模型设计

出租车轨迹数据由于其具有数据量规模大、数据类型多的特征，以至于在单机环境上难以进行处理和计算。为了提高数据处理效率，本文将大量出租车轨迹数据上传至分布式集群环境中，通过Hadoop的Ma? pReduce计算编程原理，来实现K-means的聚类，建立基于MapReduce的K-means算法模型。

设计思路如下：

1） 随机选取k个样本轨迹数据为初始簇中心，同时随着迭代更新簇中心。

2） 在Map阶段，计算每个样本轨迹点与各个簇中心的距离，并且找出距离最近的簇中心。

3） 在Combine阶段，将Map的输出在本地做进一步的合并，记录每个簇中样本的个数。

4） 在Reduce阶段，重新计算获取新的簇中心，判断结果是否收敛，否则进入下一轮迭代。

具体实现步骤：

1） 首先创建一个configuration以字符串的形式来存放初始轨迹聚类中心。

2） Mapper：重写setup方法，用来取到configuration 中的初始簇中心或上一轮聚类后的簇中心。map方法里，输入key为偏移量，value是一行样本轨迹数据，将每一个的输入样本轨迹数据点与簇中心计算出距离，并找到距离最近的簇中心。最后输出key为距离最近的簇中心，value为样本轨迹数据点。获取距离最近的簇中心的部分伪代码如下所示：

辅助变量min记录最小距离，初始化为最大值；

index记录最小距离的簇质点，初始化为0；

//计算每个输入点与簇质心的距离，并且找出距离当前点的最近簇质心

for i=（）to k-1 do{

d=样本轨迹点与第i个簇中心点的距离，采用欧氏距离

if min=ind>d {

min=d;;

index=i;

}

3）Combiner：输入为Map阶段计算得来的最近距离的簇中心和样本轨迹数据点。以划分到一个簇中心的所有样本轨迹数据作为一个簇，将相同簇下的所有样本轨迹的坐标值累加求和，为了计算每个簇的平均值，同时记录下每个簇里的样本轨迹点个数，并输出。

4） Reducer：以Combine 阶段的中间结果作为输入，将获取到的每一个簇中所有样本轨迹的坐标值累加和结果除以对应簇中样本轨迹点个数，可得到新的中心坐标，即为新的簇中心。同时，将上一轮的簇中心坐标与新的簇中心坐标做对比，若不同则在自定义的counter上加1，进入下一輪迭代。若相同，则将新的簇中心作为结果输出。

5） 在Main方法中，定义了configuration获取输入文件的路径，以及自定义了全局变量counter作为计数器。configuration在第一轮读取我们自定义的初始轨迹簇中心，而后每一次迭代都将读取上一轮计算后的新的簇中心。若计数器counter用来判断统计目前迭代次数。

4 实验结果与分析

4.1 城市道路拥堵情况

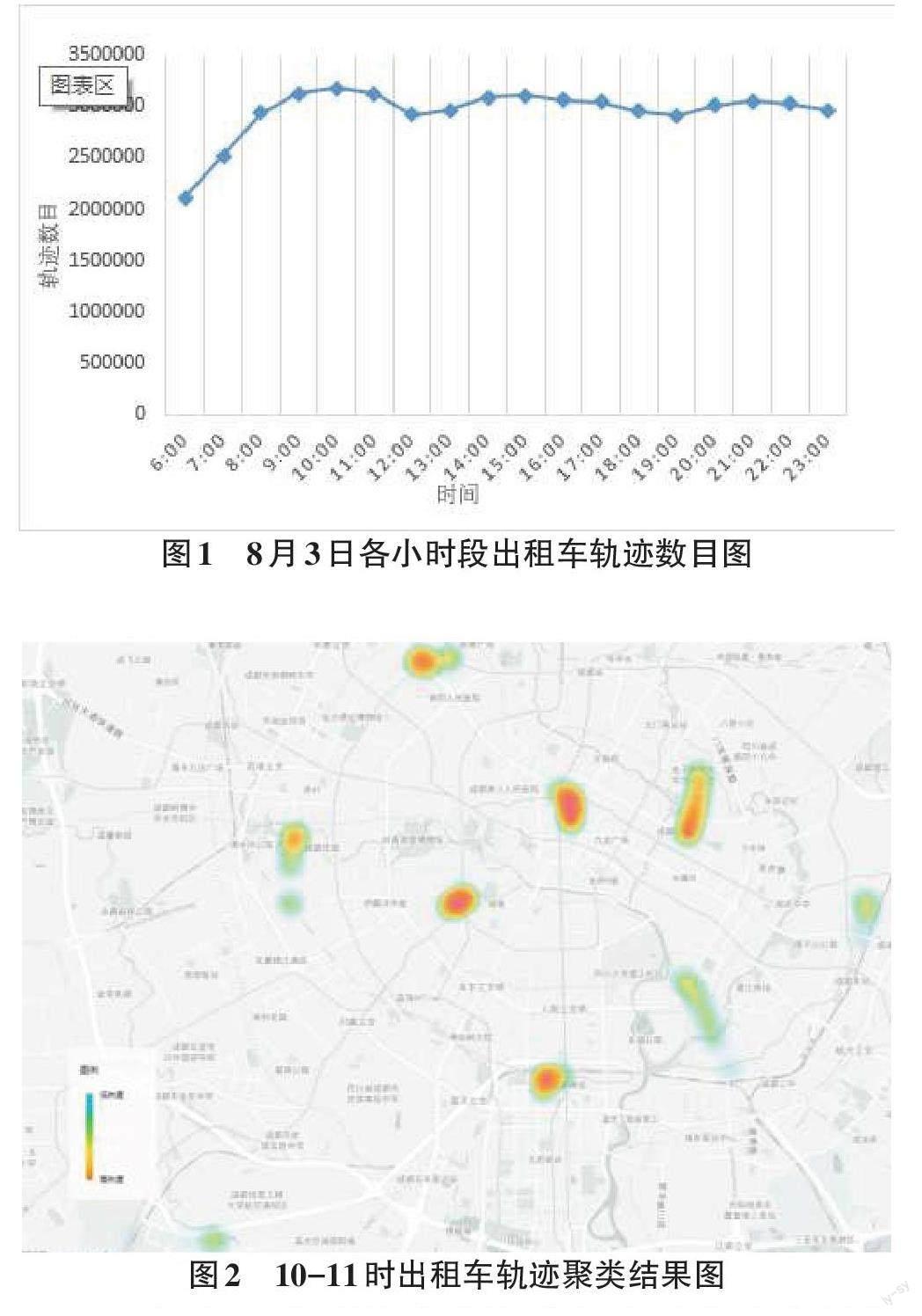
由于出租车在运营过程中受时空条件的制约，呈现不同的时间段有不同的规律。在原来经过清洗的出租车轨迹数据的基础上，针对早上6点至24点，每个小时段所有出租车行程轨迹进行统计。如图1 所示。

从图1中的结果可以看出，出租车轨迹数目在8 月3日这天呈现出3个高峰期，分别在10：00-11：00、0104：-0101-：0105：之00间以达及到2一1：0天0-之22间：0的0这最几高个峰值时，间也段就内意。味1着0：在这个时间段内处于一天之中的交通高峰期。

通常情况下，交通高峰期会出现道路堵塞、交通瘫痪等众多交通问题。为了更直观地获取城市道路拥堵情况，选取交通高峰期10：00-11：00这一时段来进一步研究。

结合K-means算法模型，设定初始聚类轨迹数目K=15，随机选取地图中15个坐标点作为初始聚类中心进行聚类，并通过多次迭代并记录每一次迭代的聚类中心和所属的轨迹数目。最后将聚类结果导入地图中。在进行了7次迭代后，获取结果如下图2所示（轨迹数目作为热度依据）。

通过图2中得到的聚类结果来看，成都市出租车在8月3日10：00-11：00这一交通高峰期内，出租车轨迹热度较高的区域大部分位于三环内，主要集中在市区的中心区域、重要的大型商场和写字楼以及公共的重要交通枢纽。

4.2 出租车载客情况

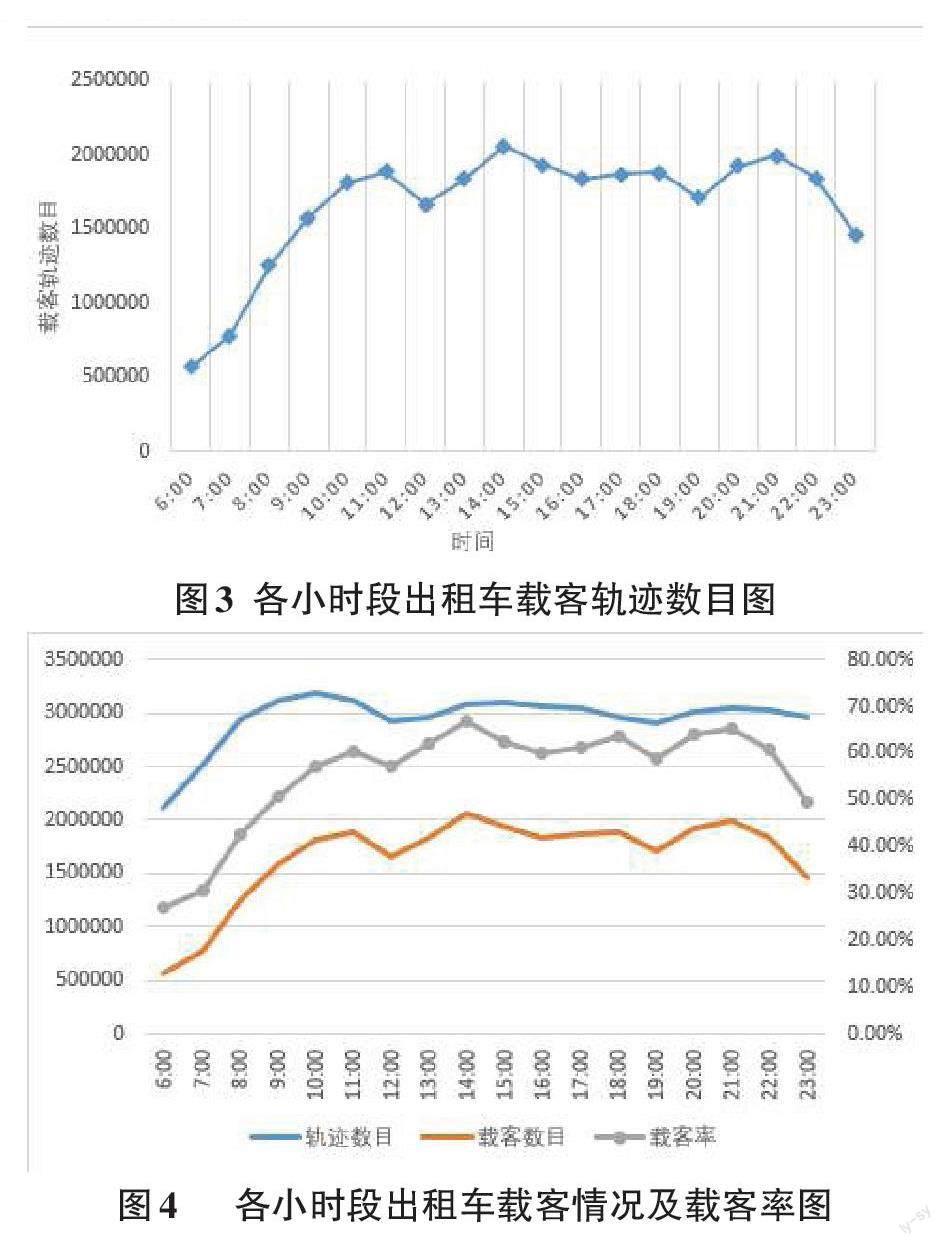
通过对预处理后的出租车轨迹数据提取载客状态为1的部分就可以得到所有载客轨迹。同样的，以每个小时为间隔来进行载客轨迹数目统计，并根据所有轨迹数目算得对应时段的出租车载客率，得到结果如图3、4所示。

从图4中可以明显地发现，在成都市8月3日按小时段的载客轨迹数目曲线与包含所有轨迹数目的曲线有相似的特征，按小时段的载客轨迹数目的3个峰值时段11：00-12：00、14：00-15：00、21：00-22：00与所有轨迹数目的3个峰值时段10：00-11：00、14：00-15：00和21：00-22：00大致相吻合。居民对于出租车的需求从8：00左右开始逐步呈现上升趋势，中午12：00-13：00是午餐用餐时段，到达第一个谷点，至13：00之后再次稳步上升，在14：00-15：00之间达到一天中的载客数目最高峰值。过了15：00之后，载客数目渐渐趋于平缓，并且在19：00时达到了一个相对较低的水平，一直到20：00左右开始回升。

载客率曲线更是几乎与载客轨迹数目完全相同。出租车的载客情况随着城市交通量的上升而增长，同时也伴随着载客率的上升。可见在处于交通高峰时段里，出租车往往都会往出行需求量大的区域汇集，这也符合出租车司机的运营策略。

4.3 居民出行热点区域划分

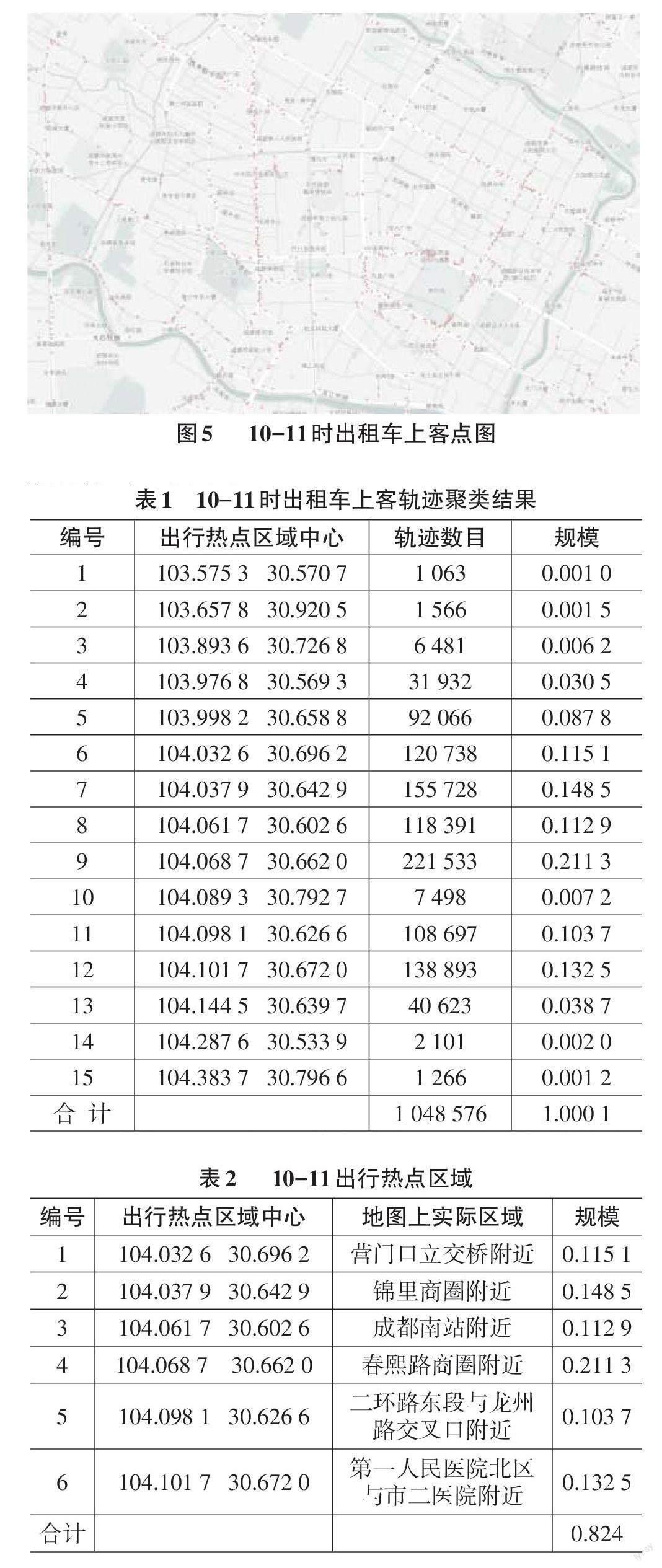
通过对预处理后的出租车轨迹数据里提取上下客点数据，来作为居民出行热点区域进行划分的依据。不同于所有轨迹，上下客点作为居民出行活动的起讫点，一定程度上反映了该居民的出行需求。本文通过获取城市交通高峰时段10：00-11：00的出租车上客点轨迹，重点分析居民上客点产生的需求，来对居民出行热点区域进行划分。获取结果如图5所示（仅部分轨迹展示）。

针对图5中出租车上客散点图来看，成都市市中心附近频繁发生上客事件主要分布于东城根街、春熙路商圈、成都第三人民医院、市二医院以及新华大道与红星路交汇处附近。以此来看，在8月3日，成都市市中心附近居民出行需求大多以休闲娱乐、医疗为主。

根据上述的成都市居民出行特征，结合K-means 聚类挖掘居民出行热点区域，并统计各热点区域上客数目，如表1所示。

观察表1可以发现，其中含有不少聚类规模较小，不具备实际分析意义。故将其剔除，同时将出行热点区域中心点与地图中实际区域相匹配，得到实际热点区域如表2所示。

通过表2的结果可以发现，以上划分出的7个热点区域的出租车出行热点轨迹规模占据的规模达到了82.4%。同时，这些出行热点轨迹的实际区域也吻合于图5二环内市中心的居民上客需求较高的区域。这几个区域体现了成都市8月3日早高峰时段10：00- 11：00居民出行的热点。

5 总结

近年来，随着大數据技术的兴起，为各种海量数据的分析研究带来了无限可能。本文以大规模的出租车轨迹数据作为分析研究对象，介绍了出租车轨迹数据的特征，并通过导入地图进行轨迹数据展示。对实验环境Hadoop平台进行了相关阐述，并在实验之前对原始轨迹数据进行预处理操作。简单地介绍了机器学习和相关常见的聚类方法。采用MapReduce 编程，建立了一个K-means聚类模型，设定了K值、初始聚类中心等相关参数，选取欧氏距离进行聚类过程中轨迹点距离的计算。结合K-means聚类模型，分析了成都市8月3日各个小时段的道路拥堵情况，并获取到了交通高峰时段的出租车轨迹热度较高的区域。通过提取出租车轨迹载客状态，展示了各小时段的载客状态载客情况和载客率，根据结果对比验证了载客率与城市交通情况存在正相关规律。对于城市居民出行热点区域的分析提取了所有轨迹数据中的上客点，通过分析交通高峰时段10：00-11：00期间所有的上客点，划分出6个出行热点区域。