长江中游典型河段岸滩稳定性评价研究

熊海滨 谭政 胡小龙 孙昭华

摘要：

岸滩稳定是岸线开发利用的前提。针对局部岸滩稳定性缺乏系统量化评估方法的问题，引入层次分析法-综合指数法，分析了来水来沙、边界条件对岸滩稳定的影响，构造了以近岸泥沙输移、主流摆动、边坡形态、河道形态及近岸泥沙组成（各因子权重占比分别为34.3%，25.7%，23.0%，9.9%，7.1%）为评价因子的岸滩稳定性评估层次模型，明确了各因子对应量化指标及稳定性综合指数的计算方法。模型在长江中游典型河段——武汉河段中下段的应用结果表明：该河段内顺直河道与分汊河道交界附近岸段稳定性相对较差，河道进出口、节点位置岸段稳定性相对较好，且右岸总体稳定程度大于左岸。提出的综合指数能较好地识别河道两岸不同位置的稳定程度，评估方法简单、可靠，可供其他类似河段评估应用。

关 键 词：

岸线利用； 岸滩稳定性； 评价体系； 武汉河段

中图法分类号： TV223

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2023.08.007

0 引 言

作为岸线资源自然属性的关键因子，岸滩稳定性（亦称岸线稳定性）是所有沿岸工程均需关注的基本问题。岸线开发利用中的稳定岸线是指长期处于基本冲淤平衡状态的岸线，强烈侵蚀、淤积岸线均为不稳定岸线［1-3］。长江岸线是珍贵资源，合理而高效地利用这些岸线的前提是对岸线稳定性有充分认识。但作为大型冲积河流，长江中下游许多河段存在主泓不稳定现象，一旦主泓近岸顶冲则会导致岸坡崩退，而主泓摆离岸线则会导致近岸淤积。經过近10 a来的岸线治理，许多岸段实施了守护工程，但这些工程仅可防止岸线崩退，并不能防止近岸淤积。尤其是三峡水库建库后，水沙条件变化导致许多河段出现新的河势调整，将可能在局部位置使原本稳定的岸线变得不稳定，亟需综合水沙条件、河势条件等量化指标，提出一套评估和预判岸线稳定性的方法体系。由于岸滩稳定性受诸多因素影响，如何定量评估进而预测岸滩稳定性存在一定难度。

目前不同学科学者对此展开了大量研究。

资源利用、地理学方面对于岸线稳定性的判断大都直接从岸线的冲淤结果出发。例如程久苗［4］根据遥感航片中岸线形状的特征及其位于河道位置情况，目视解译出冲刷岸线和淤积岸线；王传胜等［1］和秦丽云［3］引入了河演分析的一些方法，结合不同河型的稳定程度、主流线摆动、江岸顶冲部位以及冲淤变化等相关描述，进而评价了岸线的稳定性。不难发现，以上评价的标准均为定性判断，虽然简便可行，但存在较大的主观臆断性。尽管有研究以冲淤特征值的大小来量化岸线的稳定程度［4-5］，但仅以河岸处的冲淤结果来反映岸线稳定程度，而忽略了整个河势的稳定程度，显然不够全面。

河流动力学中关于河岸稳定性的研究主要有两个方面成果。① 将河岸稳定性与河床稳定性统一起来，从河段整体的角度去考虑，从河型的判别、转化目的出发，与河型稳定性研究密切相关。例如单独反映河岸稳定程度的横向稳定系数［6］以及同时考虑横向稳定性和纵向稳定性的综合稳定系数或指标，且后者更为多见。这些反映河床综合稳定性的指标或基于天然河道、模型试验得出［7-8］，或基于相关公式及理论推导而来［9-10］，也有采用层次分析法的多因素分析建立的［11］。尽管这些指标公式为描述河岸、河势稳定性提供了量化判据（各种指标公式虽然形式各异，其考虑因素概括而言无外乎来水来沙条件、河床周界条件等），但它们仅能用于不同河流或同一河流长河段中不同河型的特征参数对比［12］，这种长河段的整体稳定性显然不等同于岸线利用所关注的局部岸段稳定性。② 崩岸作为河道横向变形、岸段失稳破坏的典型现象，学者对其影响因素及临界指标亦有较多研究［13-14］。例如唐金武等［15］提出了用稳定岸坡作为崩岸判别指标；邓彩云等［16］构建了较为全面的河岸稳定性评估指标体系结构；孙启航等［17］提出了河岸崩塌评价层次结构模型。不少指标在天然河道崩岸段的检验中都取得了良好效果，但崩岸本质上是冲刷导致的失稳，因此以上关于崩岸影响因子的指标也均是考虑冲刷性质方面。而岸线资源利用评价中，淤积和冲刷均为不稳定因素［18］。若沿用崩岸指标，淤积岸线则会被视为稳定岸线，这显然也是有问题的。

总体而言，过去的河势稳定研究，其定位是以主泓位置为代表的平面形态总体稳定性，空间尺度较大，不能准确刻画出局部岸线稳定；过去的岸线稳定研究，以侵蚀崩岸区为对象，其目的是筛选需要实施防护工程的位置，而对可能淤积的位置重视不够，不能为生态、取水、港口码头等岸线利用类型提供足够支撑。有鉴于此，本文通过引入河演分析中河势稳定性的影响认识成果，建立了一套量化评估局部岸线稳定性的指标体系，提出并计算了岸滩稳定性综合指数，并对典型河道岸线开展初步应用。

1 评估方法与岸滩稳定性影响因素分析

1.1 评估方法

岸线稳定性评估采用层次分析法（AHP）-综合指数评价方法，其中层次分析法是最为常用的一种权重赋值分析方法，综合指数评价法属于常规的多指标综合评价法，二者有机结合，提高了评价结果的可靠性和有效性［19］。这类量化评估方法在生态系统健康、水资源承载力评价等领域内被广泛采用［20-21］。

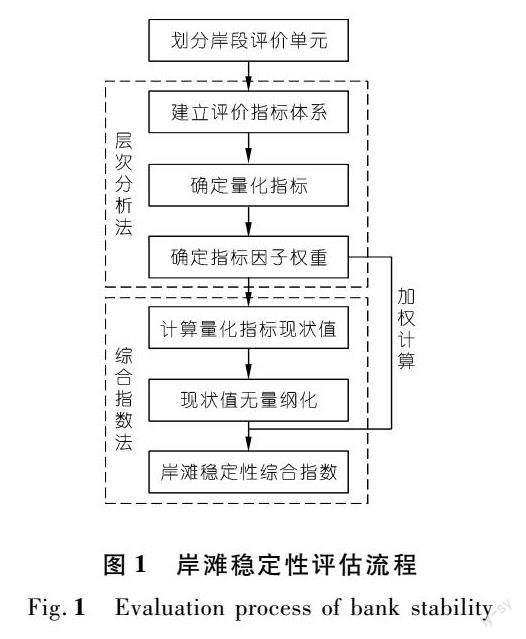
本文评估方法的流程见图1，其步骤主要如下：

（1） 划分岸段评价单元，划分过程中需考虑区段内一致性和区间差异性原则［22］。

（2） 基于相关理论分析（本文为河流动力学、资源利用学及河道自身演变特征分析），建立评价指标体系，并最终以目标、准则、指标（分别对应第一、二、三层）等多层次结构展现。

（3） 确定指标因子权重及量化指标，采用实测数据计算各量化指标的现状值，通过相关方法（本文采用五等分法）换算为无量纲的“量化值”。其中权重值确定过程中根据常用的1～9标度法来分层次对不同因子进行两两比较以构造判断矩阵，当矩阵的一致性指标CR<0.1时，认为满足一致性检验，计算方法参考文献［23］。

（4） 最后根据指标因子权重和“量化值”加权得到综合评价指数，评估结果是一个具体的数值，评价过程较简单、易于操作和使用。

1.2 岸滩稳定性影响因素

岸滩稳定本质是河道稳定的一部分，其影响因素无外乎来水来沙条件和河道边界条件。

1.2.1 水沙条件

（1） 河道来流量的影响。通常采用水文统计中的变差（离势）系数Cv表征流量变化程度（为进一步突出汛期洪峰过程的作用，亦可采用洪峰变差系数Cvf或汛期流量变幅来表征），来流系列中Cv值（或Cvf）越大，表明流量相对于均值越离散，河势、岸滩稳定性越差。但这仅能反映流量变化对长河段演变的影响，是一个河段整体稳定性指标，无法反映河段内局部岸段稳定性的差异。

河道主流线是河道水流运动的重要特征之一，水动力轴线因流量不同而产生摆动，理论上流量分配越不均匀，主流摆幅越大，岸滩越不稳定。因此，选取河段内区间主流摆动情况作为间接反映流量变化对岸滩稳定性影响的衡量指标。

（2） 河道来沙量的影响：冲积河流一般是悬沙参与造床［7］，通常以水流中泥沙含量（S）与其携带泥沙的能力（S*，常采用张瑞瑾公式）相对大小来反映来沙对河道的影响。例如姚爱峰等［11］将S/S*作为评估河流稳定性的一个指标，并认为比值越大，越稳定。但S/S*本质上应该是一个抗冲性指标，认为淤积中的河流也是稳定的。对于岸线开发利用来说，近岸处河床的强烈侵蚀和淤积均对岸线开发利用不利，应是二者偏离程度越大，越不利于局部岸线的稳定。

但一方面，泥沙观测难度和工作量很大，岸滩冲淤由连续水沙作用所决定，只有大的水文站会开展逐日泥沙数据的观测，故此指标也只适用于长河段或不同河流的整体稳定性判别；另一方面，泥沙输移运动过程中不同粒径泥沙存在粗细交换现象，运动规律尚未完全明晰。有鉴于数据获取的困难性及泥沙河道输移过程中微观机理的复杂性，有学者直接以河岸附近的冲淤结果作为衡量指标［24］，这在岸线资源评估领域也被广泛采用［3-4］。故采用冲淤结果作为间接衡量指标。

1.2.2 河道边界条件

（1） 河道纵比降的影响。该值反映的是河道纵向地形情况。尹学良［25］认为，来水来沙一定时，比降过小，挟沙力较弱，河槽发生严重淤积时将导致河槽改道不定而多汊散乱；比降过大，水流强度越大，容易发生切滩改道而变为多汊散乱。钱宁等［7］认为游荡型河流具有更大的比降，致使水流有更大的动能，加大了河道的冲淤变幅，不利于河床稳定。弯曲型河流尽管坡降缓，但始终保持着能高效输沙的窄深河槽。天然河道常用希尔兹数的倒数φv=（ρs-ρ）d/（ρhJ）反映河床在纵深方向的稳定性，并认为该值越小，河道越不稳定。

无论是比降还是考虑比降的稳定系数，均是作为大尺度范围内不同河型的稳定性对比，对于局部岸段的稳定或许就不适用了，这是因为河床纵比降一般较小，局部纵比降则不然，可能达到比较大的数值［7］。说明比降大小除与河道本身形态有关外，还受选取的河段长度影响较大。对于河段内不同岸段纵比降变化不大的河流而言，由于计算岸段长度不同带来的误差影响，使得不同岸段比降的对比分析意义不大，在进行局部岸段稳定性分析时可不考虑纵比降因子。

（2） 河道宽深关系的影响。该值反映的是河道平面形态。宽深差异更多的是由于河岸抗冲性不同所造成的结果，相对于河床组成，岸边组成抗冲强度越大，就易形成窄深断面，不然就会向宽浅方向发展［11］。此外，河演分析中应用较为广泛的横向稳定系数φh=Q0.5/（J0.2B），亦包含了河宽的参数［12］，认为河道越宽浅，稳定程度越低；反之，河道越窄深，其越稳定。以河宽或宽深比来作为河岸稳定性指标，本质上是间接用河岸变化的结果来描述其稳定性。

通常而言，河道束窄处一般由天然矶头节点控制；而河道放宽处，河道为了与水流条件相互适应，常生成边（心）滩，岸滩活动性强。显然，束窄段的岸滩稳定程度大于放宽段。因此，本项研究采用宽深比B/h作为岸滩稳定性指标之一。

（3） 边坡形态的影响。该值反映的是岸滩坡度情况。唐金武等［15］结合长江中下游河岸崩塌特征，提出了以稳定坡比来识别岸坡的稳定程度，并考虑了不同河型、不同地质组成及护岸工程对稳定坡比阈值的影响。相关研究表明，岸滩坡度越陡，越容易崩塌和冲刷，越不稳定；反之，则越稳定。因此，选取近岸岸坡坡度作为岸滩稳定性指标之一。

（4） 床沙组成的影响。河床表层泥沙直接受到水流的作用力，决定了河床的可动性，其抵抗水流作用力的大小与泥沙粒径密切相关。研究表明，无论室内试验还是天然河道观测［26-27］，在特定水深条件下均存在泥沙临界粒径，当泥沙颗粒大于该值时，其受重力作用占主导，粒径越大愈难以起动；泥沙粒径小于临界值时（通常为黏性土），颗粒间黏结力占主导地位，粒径越小愈不易起动。由于天然河流床沙组成的非均匀性，常用中值粒径D50代表，故近岸带床沙D50可作为衡量岸滩稳定性指标之一。需注意的是，长江中下游在枝城以上存在局部基岩出露或者胶结卵石层等特殊边界，河岸抗冲性强。本文主要考虑枝城以下的沙质冲积河段，其岸坡多为沙质。

2 岸滩稳定性评估层次结构模型

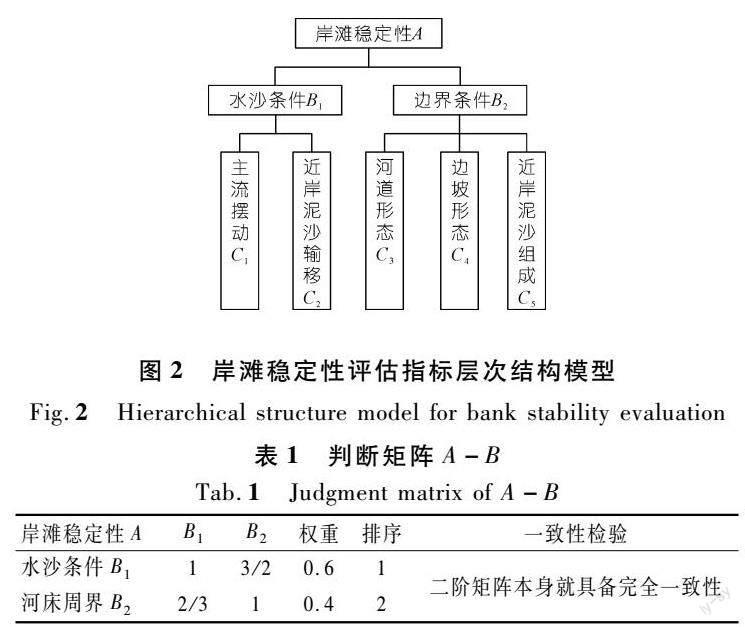
2.1 评价指标体系构建

根据以上分析，岸滩稳定性评估层次结构模型如图2所示，岸滩稳定性作为目标，列为第一层，水沙条件、边界条件为第二层。水沙條件包括主流摆动、近岸泥沙输移2个因素；边界条件包括河道形态、边坡形态和近岸泥沙组成3个因素，共计5个影响因子。其中，考虑到深泓摆动与主流摆动有较好的一致（跟随）性，且一般河道内深泓观测资料较为丰富，因此本文采用深泓摆动幅度作为量化指标。最终确定分别以深泓平均摆幅、近岸冲淤厚度、宽深比、坡比和中值粒径作为具体量化指标。需要说明的是，本文并未在指标中单独设置工程影响，但岸坡形态（坡比）分析中一定程度上间接考虑了护岸影响。

2.2 影响因子权重的确定

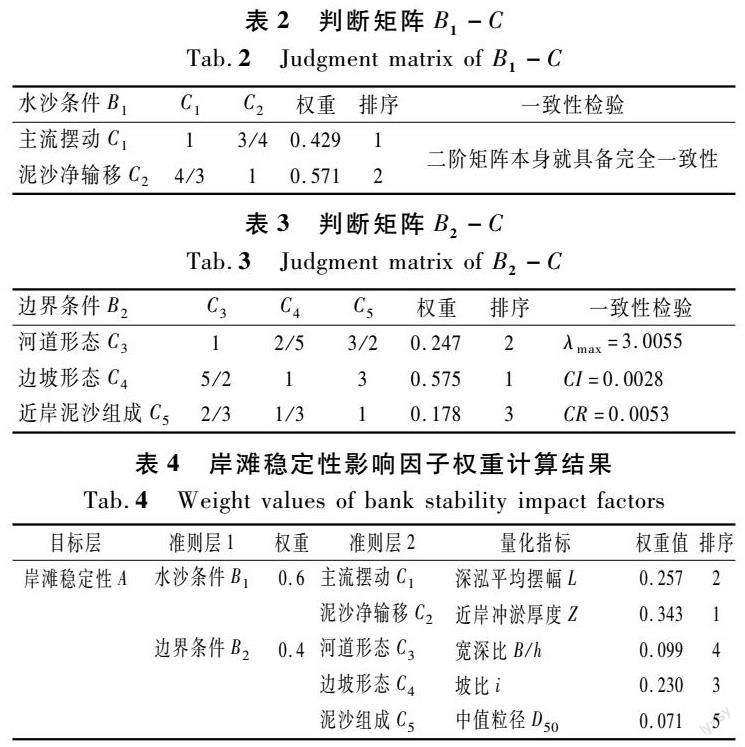
采用1～9标度法对以上影响因子进行两两比较，得到权重大小的量化值。在岸滩演变分析中，无论是河床综合稳定判断还是崩岸的研究，水沙条件均被认为是影响岸线稳定性的主导因子［11，17］。对于冲积平原河流而言，主流变化贯穿于岸线、滩槽演变之中，其摆动频繁常导致航槽位置多变［28］，尤其是对河岸崩塌和淤积的影响，在某种意义上讲是起决定性作用的。而来沙量的多寡则决定了泥沙的冲淤幅度［29］。因此确定水沙条件比河床周界重要，B1比B2的标度为1.5（见表1）。

水沙条件中，主流摆动幅度越大对岸线稳定性越不利，主流近岸则顶冲岸边，远岸则易于淤积，某种程度上甚至对岸滩形态变化起决定性作用。近岸泥沙净输移在宏观上表现的即是近岸冲淤情况，其绝对值越大，说明岸线越不稳定；除泥沙的绝对来量以外，来沙中床沙质占比亦有重要影响：尽管它一般只占运动泥沙的少数，粗颗粒的床沙质却是与河床中泥沙交换并对河床起塑造作用的主体。钱宁等［7］认为，来沙中粗颗粒泥沙或床沙质占比越大，河道越容易游荡摆动，对其稳定性越不利。反之，一定程度的冲泻质可使河流向稳定的河型发展。因此，两者都是极其重要的单项因子，考虑到地理学中对岸线稳定性评估均采用近岸冲淤作为重要甚至是唯一指标［1，4-5］，因此确定后者相对于前者略重要，重要程度在同等重要和稍微重要之间，C2比C1的标度取1.33（见表2）。

考虑到边坡坡度在某些文献中是岸滩失稳的主要判别指标，如唐金武等［15］利用稳定岸坡来衡量河岸的稳定性，能较好地预测天然河道具体失稳位置。因此首先确定边坡坡度比河道形态和近岸泥沙组成均更重要。河道形态反映的更多是河势情况，格鲁什科夫早在1924年就提出了用宽深关系表征河相系数ζ=B/h，河岸越稳定和不易冲刷，ζ值越小；窦国仁［30］提出的最小活动性假说中认为，河岸土壤越稳定，宽深比B/h就比较小。反之河岸越稳定其宽深比就比较大，如河床及河岸易冲的游荡型河流河槽断面均为宽浅型［31］。

相比于河道形态，近岸泥沙组成比局部岸滩边界重要，确定C4相对于C3标度为2.5，C3相对于C5标度为1.5（见表3）。

经分析，各判断矩阵均满足一致性检验。综合各判断矩阵，得到岸滩稳定性影响因子的权重值最终计算结果见表4。

3 实例应用

3.1 典型河段选取

武汉河段中下段由顺直（微弯）单一河道和分汊河道组成，是长江中游典型河道形态。此外，学者们对于该河段两岸边滩演变机理的研究较多，相关结论可对模型评估结果准确性提供支撑，故选取该河段为典型河段开展研究。

岸段评价单元划分是岸滩稳定性评估的前提和基础，本文参考航道部门在河段内施测的水文断面数据，结合河流入汇流位置，将研究河段左、右岸地区共划分为22个评价单元（见图3）。划分依据是：一方面这些水文断面已能较好反映河型、滩槽转换等特点，确保划分后的评价单元能较好地反映岸线自然属性的空间分异特征［2］；另一方面也可充分利用断面上丰富的水文泥沙观测数据对岸段进行评估。

3.2 数据情况和指标分析

结合实测资料对22个岸段评价单元对应的5项指标分别展开计算，研究中所采用的数据见表5。其中断面水沙数据主要用于计算宽深比、中值粒径；地形数据则用于计算深泓摆幅、冲淤速率和坡比。

研究河段内不同断面流速观测表明，河道主流随流量变化存在左右、上下摆动特性，沿岸大流速区和缓流区的位置也随之变化，不同岸段内主流摆动幅度有显著差异，主流过渡区、分汇流区（汊道进出口）段的主流摆幅明显大于其他区段。对应地，这些位置的岸滩稳定性相对较差［32］，即主流摆动幅度越小，越利于岸滩的稳定。岸滩冲淤速率可根据包含有典型水文年区间（包含有大、小水沙年）的两套不同年份地形CAD测图散点数据通过作差计算得出，冲淤速率值越小，说明岸滩越稳定。由河段内各断面沿岸纵比降统计可知，各断面间纵比降在2.5×10-3上下波动，变化相对不大［33］；加之由于计算岸段长度不同带来的影响，本次研究中不考虑纵比降因子。对于武汉河段来说，河宽最窄深处由山-蛇山矶头节点控制，稳定程度明显大于放宽段，也即宽深比B/h越小，岸滩越稳定。武汉河段由沙质河床组成，近岸带床沙D50越大，河床的可动性越低，其稳定性越好。综上，除中值粒径是正向指标外，其余均为负向指标，也即前者数值越大对应评级越高，后者则相反。

3.3 计算方法

以下按权重值大小降序对不同指标的计算方法和过程进行简要介绍。

（1） 由于坡面和坡脚冲淤均不利于岸坡稳定，且近岸涉水建筑物大都侵占一定陆域和水域面积，故冲淤厚度计算范围考虑为多年平均流量下水边线向内陆和水边平行延展一定距离。计算步骤为：将包含有典型水文年区间（本文以1996～2011年为例）的两套不同年份地形CAD测图散点数据插值在同一套细密网格上，再与水边线及左右延展范围线进行图层叠加，如图4所示（以L2、R2岸段评价单元为例）；统计各岸段评价单元两条延展线范围内的网格，则平均冲淤幅度Z可用下式计算：

式中：n为选定范围内网格数量，zi为第i个网格冲淤值，Ai为网格单元面积。

（2） 20世纪90年代以后研究河段深泓平面摆动趋向稳定［34］，因此，深泓计算以1993年为起点，在CAD中将各测年的深泓摆动最大点连接，形成兩条外包线（见图5）。则深泓平均摆幅L=A/B（A为岸段内外包线包围面积，B为岸段长度，二者均通过CAD软件获取）。当深泓为单一段时，对应位置的左、右岸段评价单元对应A相同；深泓分汊处岸段评价单元取对应侧的深泓摆动面积。

（3） 岸坡计算参考了文献［15］中的计算方法。图6同样以L2、R2岸段评价单元为例，选取评价单元内上、中、下游3个典型横断面，分别计算各断面的左、右侧的坡比，如岸段评价单元上游断面的坡比

为点AL2-上（枯水位线与横断面交点）与BL2-上（近岸区断面最低点）连线对应的坡度，即i=|YA-YB|/|XA-XB|，其中枯水位线采用枯期（2009年3月）实测水文断面水位插值计算。岸段评价单元坡度由对应侧3个断面坡比的均值确定。

（4） 宽深比采用漫滩流量下河道宽度与平均水深之比。考虑到2011年8月洪水流量接近河道平滩流量，因此，采用该测次的断面河宽和水深数據（航道部门提供水位数据，流速记载计算表中通常会附带记录对应时刻的水面宽、平均水深等数据信息）计算断面宽深比，将上、下游断面宽深比均值视为岸段评价单元对应宽深比。

（5） 岸段评价单元中值粒径D50的计算采用有关部门在河段内不同断面开展的床沙观测数据，并以各断面左、右侧第一条垂线代表左右岸床沙组成，取上、下游断面中值粒径的平均值。图7为各断面左、右岸床沙级配图，从图上不难发现，右岸床沙组成总体较左岸更粗。

3.4 结果与分析

基于上述计算方法，对所有岸段评价单元逐一进行计算得到相应的指标具体值。为便于量化分析，统计各项指标全部计算值的最大值和最小值，组成最值区间，采用五等分法对最值区间进行均匀划分，5个区间分别对应1，2，3，4，5个评级，评级越高越优。由于冲淤均对稳定性不利，评级分析前需将负值进行绝对值化处理。正向指标数值越大对应评级越高，负向指标则相反。需说明的是，考虑到部分统计数据存在最值突变问题，也就是最值与其他值相差过大，如中值粒径指标，故将所有岸段评价单元中值粒径进行升（降）排序绘制曲线，可发现曲线存在明显拐点。若依然根据最值划分区间，会导致岸段评价单元的评级差异不大。为此，区间划分的临界值采用拐点以下曲线适当延展得到最值，再根据两端最值大小均匀划分为5个区间。计算结果见表6（以左、右岸前5个岸段评价单元为例）。

结合上表中各项指标的评级分（也即量化值）及对应的权重值（见表4）进行加权平均［19］，即可得到岸滩稳定性综合指数，该值可反映以上5项因子影响下的岸滩稳定程度。图8为最终计算结果，由图可知，河段内岸滩稳定性综合指数沿程分布并不均匀，岸段评价单元L7、R7稳定性综合指数最小，分别为2.63、2.31，该处岸段位于顺直河道与分汊河道相衔接的进口位置。事实上，该区域河床冲淤交替频繁，主流摆动不定，岸滩极为不稳定，屡屡发生碍航问题［32］。右岸R1、R2、R3、R6、R11及左岸L5、L9岸滩稳定性相对较好，同等条件下岸线开发利用时可优先考虑这些岸段。可以发现，河宽较窄处的岸滩稳定程度相对较高，如河道进口（L1、R1）、出口（L11、R11）及龟山-蛇山节点（L5、R5）处的稳定性综合指数均在对应平均线之上。总体来看，右岸岸段稳定性大于左岸，其中右岸的综合指数平均值为3.61，而左岸为3.32。这与底沙输移运动和岸滩频繁冲淤变化主要位于河段左岸的认识相一致［32，35］，反映了稳定性综合指数的合理性。

4 结 论

引入层次分析法-综合指数法，基于理论分析建立了岸滩稳定性评估层次模型，确定了各项指标因子权重值，明确了各单项指标及综合指数的计算方法，并在典型河段开展应用研究，主要结论如下：

（1） 岸滩稳定性由构造的稳定性综合指数反映，该指数可通过岸滩冲淤幅度、深泓平面摆动幅度、岸滩边坡坡度、河道宽深比及岸滩泥沙组成5项指标的量化值加权计算确定，各指标权重值分别为34.3%，25.7%，23%，9.9%，7.1%。

（2） 武汉河段两岸不同位置岸滩稳定程度差异较大，其中河段内顺直河道与分汊河道交界附近岸段稳定性相对较差，河道进出口、节点位置岸段稳定性相对较好，且右岸总体稳定程度大于左岸。

（3） 本文提出的岸滩稳定性评估方法简单、可靠，可在其他类似径流冲积河段开展应用。长江岸线距离长，不同河段内影响因素多，限于问题复杂性，未考虑受下游潮汐影响的感潮河段，也未考虑江湖汇流点等局部顶托以及局部采砂坑或大规模崩退导致的溯源冲刷影响，还有待今后进一步深入研究。此外，如何在指标设置中考虑人为工程的影响，亦值得探讨。

参考文献：

［1］ 王传胜，李建海，孙小伍.长江干流九江-新济洲段岸线资源评价与开发利用［J］.资源科学，2002（3）：71-78.

［2］ 段学军，陈雯，朱红云，等.长江岸线资源利用功能区划方法研究：以南通市域长江岸线为例［J］.长江流域资源与环境，2006（5）：621-626.

［3］ 秦丽云.长江江苏段岸线及岸线资源综合评价［J］.中国农村水利水电，2007（3）：13-16.

［4］ 程久苗.长江皖江段岸线资源的遥感调查及开发利用评价［J］.自然资源，1996（3）：67-72.

［5］ 杨静，李满春，丁贤荣，等.长江南京段岸线资源GIS评价与分析［J］.地球信息科学，2008（2）：200-205.

［6］ 谢鉴衡.河床演变及整治［M］.北京：中国水利电力出版社，1997.

［7］ 钱宁，张仁，周志德.河床演变学［M］.北京：科学出版社，1987.

［8］ 张红武，张罗号，赵晨苏.基于面积型Froude数的河型判数与黄河河道最大输沙流量及河槽宽深尺度［J］.泥沙研究，2019，44（2）：11-17，47.

［9］ 周宜林，唐洪武.冲积河流河床稳定性综合指标［J］.长江科学院院报，2005（1）：16-20.

［10］ 赵晓马.顺直冲积性河道河相关系和稳定指标研究［D］.重庆：重庆交通大学，2009

［11］ 姚爱峰，刘建军.冲积平原河流河型稳定性指标分析［J］.泥沙研究，1995（3）：56-63.

［12］ 姚仕明，黄莉，卢金友.三峡、丹江口水库运行前后坝下游不同河型稳定性对比分析［J］.泥沙研究，2012（3）：41-45.

［13］ 岳紅艳，余文畴.长江河道崩岸机理［J］.人民长江，2002，33（8）：20-22.

［14］ 夏军强，宗全利，许全喜，等.下荆江二元结构河岸土体特性及崩岸机理［J］.水科学进展，2013，24（6）：810-820.

［15］ 唐金武，邓金运，由星莹，等.长江中下游河道崩岸预测方法［J］.四川大学学报（工程科学版），2012，44（1）：75-81.

［16］ 邓彩云，李凌云，朱勇辉.河岸稳定性评估指标体系初探［J］.长江科学院院报，2019，36（10）：127-130.

［17］ 孙启航，夏军强，周美蓉，等.层次分析法在荆江河段崩岸影响因素研究中的应用［J］.泥沙研究，2021，46（2）：21-28

［18］ 段学军，邹辉.长江岸线的空间功能、开发问题及管理对策［J］.地理科学，2016，36（12）：1822-1833.

［19］ 李天宏，丁瑶，倪晋仁，等.长江中游荆江河段生态航道评价研究［J］.应用基础与工程科学学报，2017，25（2）：221-234.

［20］ 张婉婷，马志远，陈彬，等.福建省九龙江口红树林生态系统健康评价：基于活力-组织结构-恢复力框架［J］.生态与农村环境学报，2022，38（1）：61-68.

［21］ 丁相毅，石小林，凌敏华，等.基于“量-质-域-流”的太原市水资源承载力评价［J］.南水北调与水利科技（中英文），2022，20（1）：9-20.

［22］ 段学军，陈雯，朱红云，等.长江岸线资源利用功能区划方法研究：以南通市域长江岸线为例［J］.长江流域资源与环境，2006（5）：621-626.

［23］ 李晓璐，李春雷，李德玉，等.基于多层次模糊分析法的大坝安全评价研究［J］.人民长江，2010，41（17）：92-95.

［24］ 陈立，明宗富.河流动力学［M］.武汉：武汉大学出版社，2001

［25］ 尹学良.弯曲性河流形成原因及造床试验初步研究［J］.地理学报，1965（4）：287-303.

［26］ 张瑞瑾.河流泥沙动力学［M］.北京：中国水利水电出版社，1998.

［27］ 杨绪海，熊海滨，李义天，等.三峡水库蓄水后下荆江河段典型洲滩调整机理［J］.湖泊科学，2021，33（3）：819-829.

［28］ 刘亚，李义天，孙昭华，等.荆江河段水沙条件与主流线特征关系研究［J］.水利水运工程学报，2011（2）：77-83.

［29］ 李思璇.三峡水库调蓄对荆江水沙输移及河床调整的作用机理研究［D］.武汉：武汉大学，2019.

［30］ 窦国仁.平原冲积河流及潮汐河口的河床形态［J］.水利学报，1964（2）：1-13.

［31］ 蔡金德，樊崇良.游荡型河道的河相关系与游荡指标［J］.泥沙研究，1986（4）：83-87.

［32］ 孙昭华，冯秋芬，韩剑桥，等.顺直河型与分汊河型交界段洲滩演变及其对航道条件影响：以长江天兴洲河段为例［J］.应用基础与工程科学学报，2013，21（4）：647-656.

［33］ 张强，张小峰.采砂深度对分汊河道影响分析［J］.华东师范大学学报（自然科学版），2009（3）：127-135.

［34］ 王继全，张细兵.长江中游武汉河段近期河道演变分析［J］.人民长江，2018，49（3）：9-14.

［35］ 陈立，冯源，吴娱，等.武桥水道水动力特性与汉阳边滩演变［J］.武汉大学学报（工学版），2008（5）：1-4，39.

（编辑：胡旭东）

Abstract：

Bank stability is the premise of shoreline resources utilization.Aiming at the problem of lacking comprehensive quantitative evaluation methods for bank stability，this paper introduced the Analytic Hierarchy Process （AHP）-comprehensive index method to analyze the influence of water，sediment，boundary conditions on bank stability.A bank stability evaluation hierarchical model which includes near-shore sediment transport，mainstream swing，bank slope，channel shape，and near-shore sediment composition （the weights of each factor were 343%，257%，23%，99% and 71% respectively） was constructed，and the quantitative index corresponding to each factor and the calculation method for the comprehensive stability index were clarified.The application results of the model in the typical reach （middle and lower reaches of the Wuhan Reach） showed that the stability of the bank near the junction of the straight river and the branched river was relatively poor，the stability of the bank at the entrance and narrowed section of the reach was relatively high，and the overall stability of the right bank was greater than that of the left bank.The comprehensive index can better reflect the stability degree of different bank sections，and the evaluation method was simple and reliable，which can be applied in other similar river reaches.

Key words：

shoreline resources utilization；bank stability；evaluation system；Wuhan Reach