基于离散元方法的反倾层状岩质边坡变形破坏影响因素研究

杜 宇

(黑龙江省哈尔滨市延寿县关门山水库灌区服务中心,黑龙江 延寿 150779)

0 引 言

针对反倾岩质边坡破坏机理,国内外学者进行了相关研究。Adhikary等[1]对反倾软硬互层岩质边坡进行了离心机试验,得出反倾软硬互层边坡变形破坏特征以及相应演化规律,并提出了解决方法。Amini[2]运用理论与试验相结合的方法,分析边坡变形破坏特征,揭示了反倾层状岩质边坡破坏规律。顾东明等[3]采用离散元方法,对三峡库区反倾岩质滑坡演化过程进行模拟,结果表明龚家坊滑坡的关键控制部位为中部厚层灰岩,坡脚薄层岩体易出现弯曲倾倒变形破坏现象。姚晔等[4]对反倾层状碎裂结构岩质边坡开展基底摩擦试验,分析位移、变形、弯折角等因素对岩质边坡的影响,揭示了该类边坡破坏机制及相应空间演化规律。黄少平等[5]采用3DEC软件以及数理统计系统,对反倾岩质边坡进行了研究,结果表明当存在3个临空面时,边坡变形最大。黄达等[6]对软硬互层岩质边坡倾倒模型进行了研究,结果表明软硬互层岩质边坡的破坏模式与传统单一岩层边坡破坏模式之间存在明显差异,其破裂面呈弧线形。

上述研究主要集中在对反倾层状岩质边坡的破坏机理上,较少对该类边坡变形破坏影响因素进行研究。因此,本文基于前人研究的基础上,结合UDEC离散元数值模拟方法,对影响反倾层状岩质边坡破坏因素的敏感性进行分析,并得出相应结论,为今后工程建设中处理反倾层状岩质边坡失稳问题提供参考与借鉴。

1 工程概况

某反倾层状岩质边坡所处地段为中高山深切割地貌,深切割深度0.6～1.3km,地势险峻,高差大,地形坡度50°～70°。两岸阶地较为发育,以三级阶地为主。该边坡的破坏模式为倾倒崩塌破坏,崩塌体整体呈现喇叭状,有较为明显的倾倒弯曲变形体出露。

通过对现场进行勘察发现,该区域地层主要是第四系和上志留统,上覆层以粉质黏土为主,厚度较薄,下覆基岩为上志留统以及薄层或薄层板岩为主,分布连续,产状为NW280°～330°/SW72°～87°,边坡板理面以及岩层层理面发育较好。由于该区域存在地表常年性支流,根据预估流量,地表水冲刷作用较强。

2 UDEC基本理论

UDEC是ITASCA公司旗下的一款块体离散元软件,可用于非连续介质在动静荷载作用下时力学响应特征,基于UDEC能更为真实地模拟层状岩质边坡的破坏特征以及相应变形规律问题。UDEC离散元软件中本构模型主要分为7类:弹性模型、D-P塑性模型、M-C塑性模型、应变软化/硬化模型、堆砌节理模型、双屈服模型、M-C模型。

本文将边坡模型进行简化,通过改变边坡模型的坡高、岩层倾角等因素,分析岩质边坡结构变化对边坡变形破坏特征的影响。将边坡视为均质层状边坡,仅考虑层面结构对反倾岩质边坡的影响。岩层块体单元采用Mohe-Coulomb(弹-塑)本构模型,岩体采用摩尔-库伦本构模型,层理结构面采用连续屈服模型,层理采用库伦滑移模型。

3 反倾层状岩质边坡模型建立

3.1 细观参数标定

数值模拟的正确性取决于细观参数的确定,室内力学试验可直接获得宏观力学参数,包括抗压强度、内摩擦角、黏聚力等。而UDEC离散元数值模拟软件并未给出细观力学参数与宏观力学参数之间的定量关系表达式,因此本文采用试验结果,通过不断调试模拟试验结果,将试样的应力-应变曲线作为验证项目,得到其细观参数。

岩体参数由变形参数、强度参数两方面组成。由于岩体具有非均质、不连续等方面特点,在岩体力学中,泊松比u的变化幅度不大,远小于弹性模量E、黏聚力C、内摩擦角φ的变化。因此在计算模型中,将泊松比u当成已知量,将弹性模量E、黏聚力C、内摩擦角φ当成反演参数。

以下将针对弹性模量E、黏聚力C、内摩擦角φ进行参数反演,得到合理参数。通过细观参数标定得到的细观参数见表1;应力-应变拟合曲线见图1。

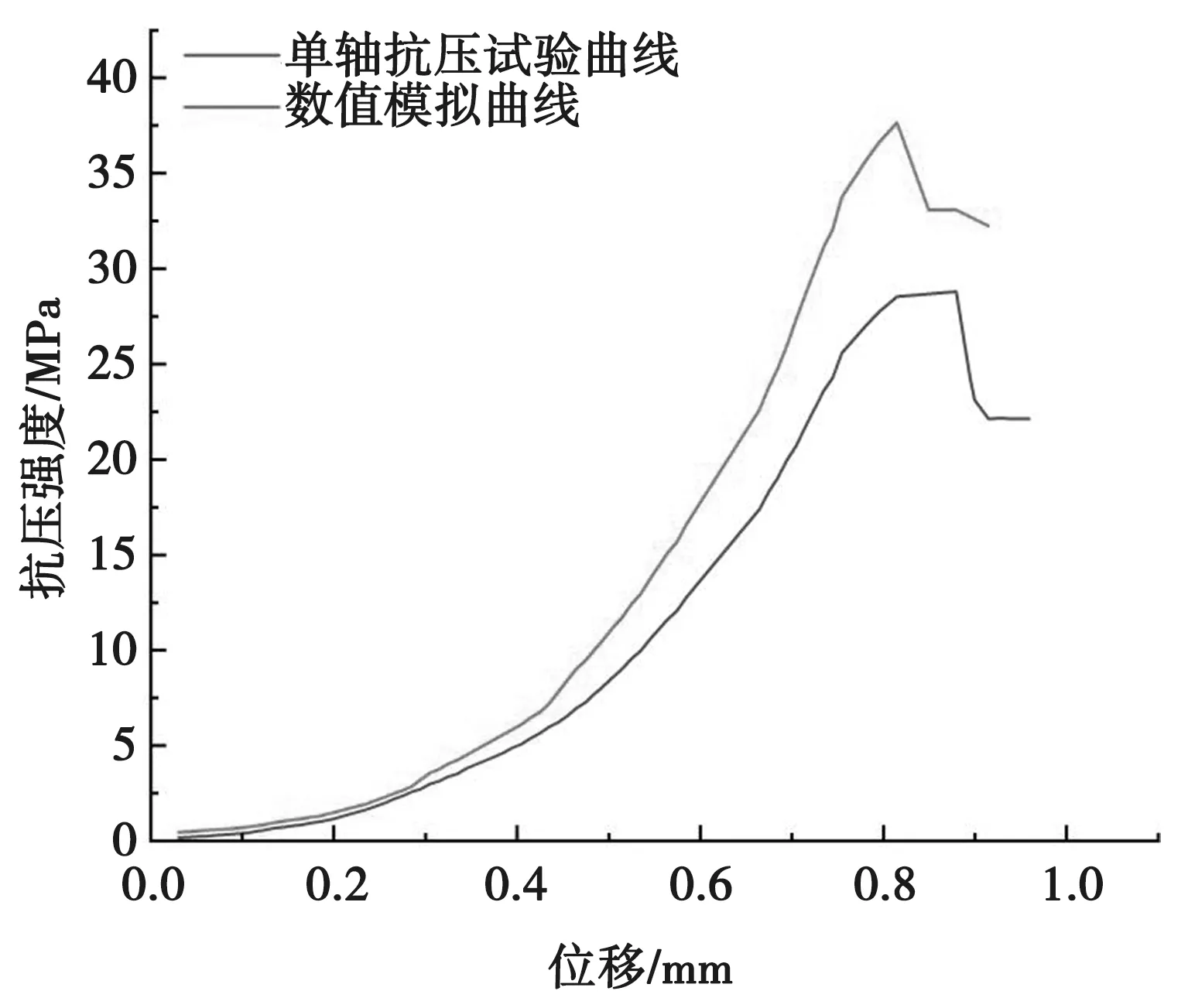
图1 应力-应变拟合曲线

表1 材料参数

3.2 三维模型建立

本文以实际边坡勘察资料为基础,建立反倾层状岩质边坡模型。由于边坡结构各因素对边坡的影响,因此在坡表以及边坡内部均布设监测点位,具体参数如下:边坡高度100m,坡度60°。监测点位布设见图2。

图2 反倾层状岩质边坡模型

4 反倾层状岩质边坡的变形破坏特征

4.1 岩层倾角

根据层状边坡特性可知,岩层倾角变化会导致层状边坡变形破坏特征发生变化,对不同岩层倾角下边坡进行数值模拟。图3为坡角60°、坡高100m时最大位移量随倾角变化图。

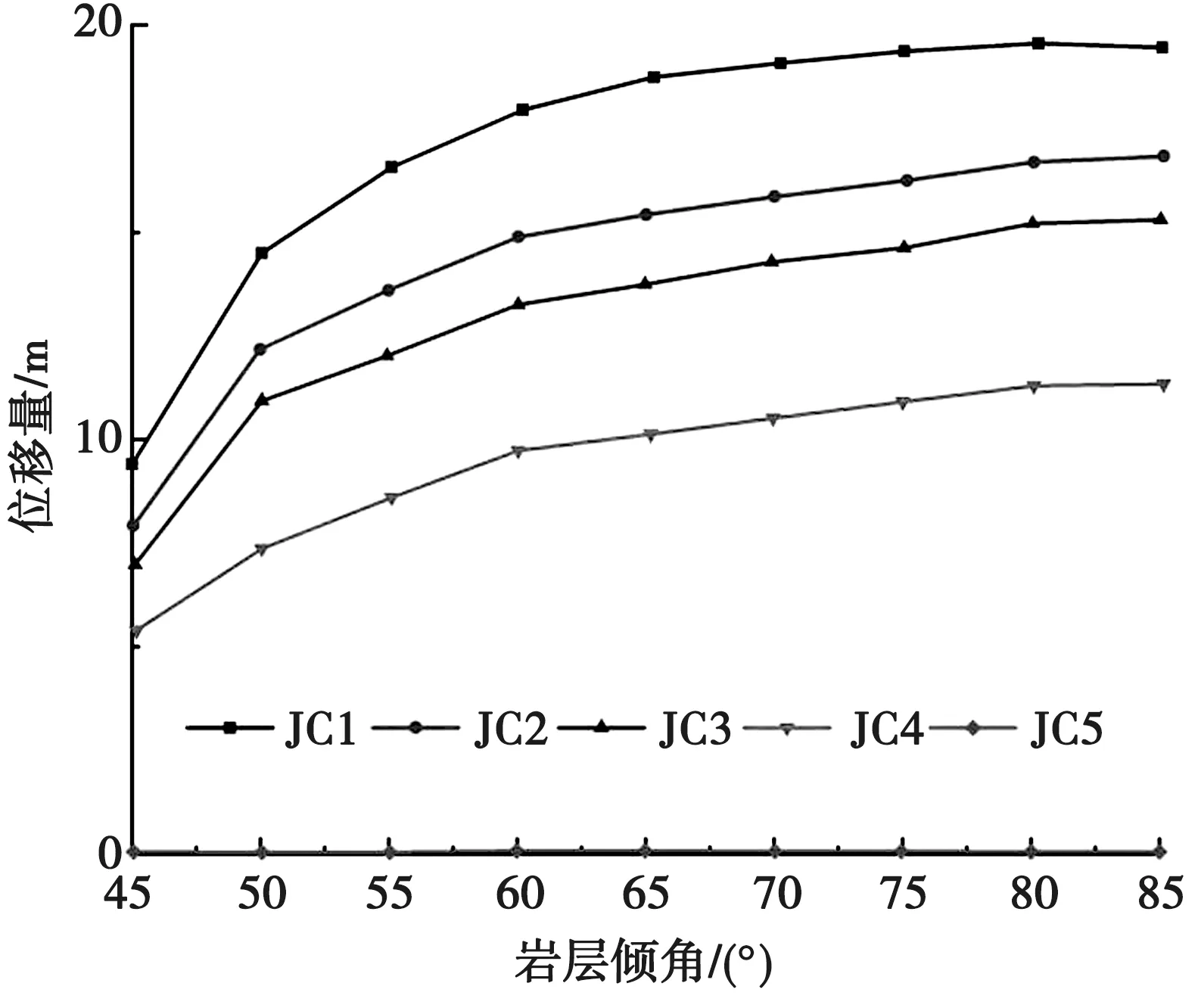
图3 最大位移量随倾角变化图

由图3可知,边坡坡脚基本不发生变形,因此JC1位移变形量较小。除JC1以外,其余监测点位的变化规律基本相同,边坡最大位移量随岩层倾角的增大而不断增大,位移量的增大程度随着边坡倾角的增大而减小。因此可以推知,岩层倾角对边坡的变形破坏有显著影响。

4.2 坡 角

坡角的不同会导致边坡破坏特征产生显著差异。在边坡坡角较缓时,边坡更稳定,不易破坏;随着边坡坡角的不断增大,边坡稳定性也随之降低,边坡易出现变形破坏迹象。

图4为岩层倾角60°、坡高100m时最大位移量随坡角变化图。

图4 最大位移量随坡角变化图

由图4可知,边坡最大位移量随坡角的增大而不断增大,位移量的增大程度随着边坡坡角的增大而增大。通过图4还可知,除JC2以外,其余监测点位所监测的位移值显示边坡位移变化增幅随着坡角的增大而增大,表明坡角的增大会导致边坡变形破坏程度严重。

4.3 坡 高

反倾层状岩质边坡的坡高不同会对边坡破坏特征产生显著影响,对不同坡高情况下边坡进行数值模拟。图5为岩层倾角60°、坡角60°时最大位移量随坡高变化图。

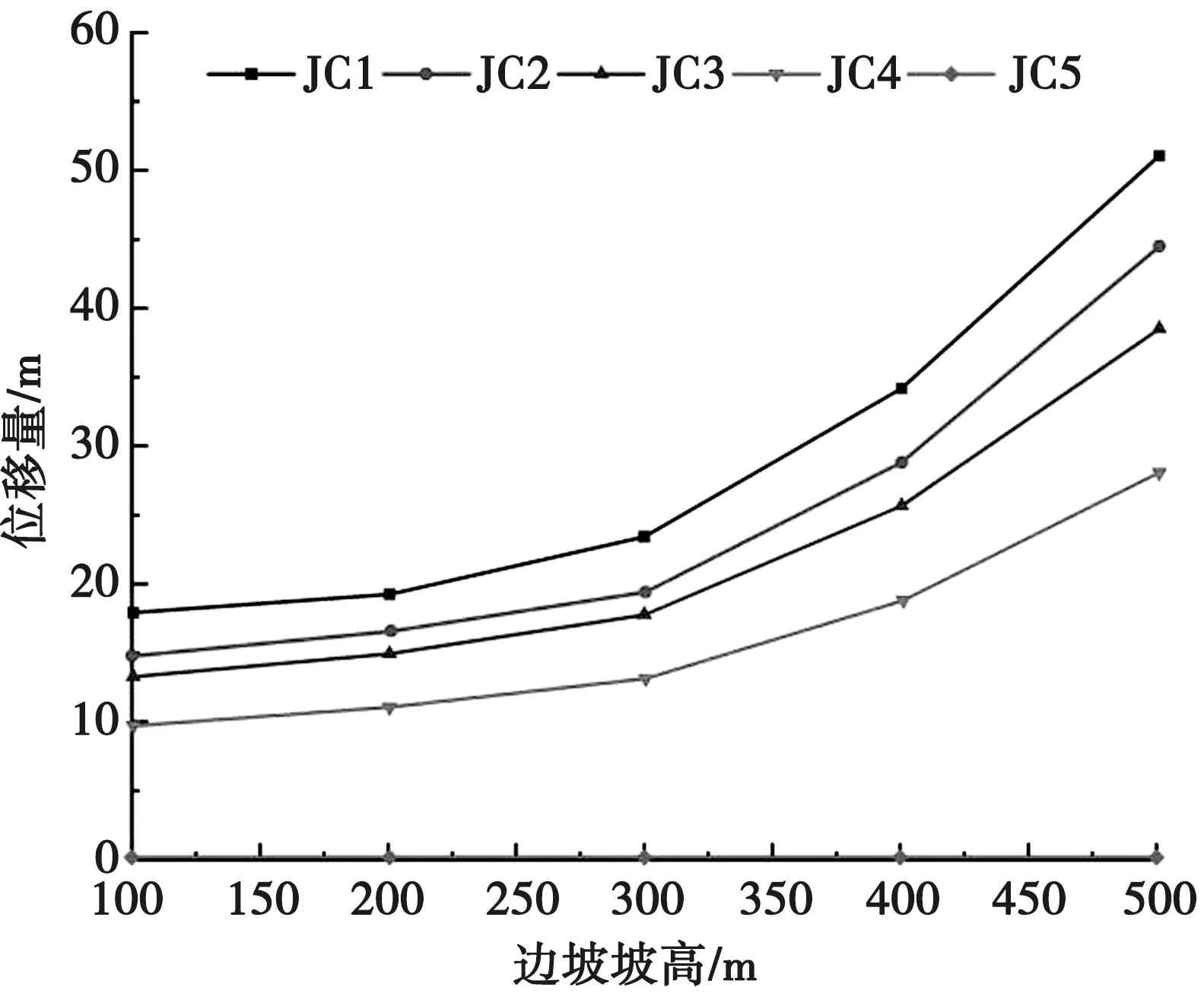
图5 最大位移量随坡高变化图

由图5可知,边坡最大位移量随坡高的增大而增大,但变形破坏模式基本不变。因此可知,坡高变化对位移量有部分影响,但对边坡破坏形式的变化基本无影响。表明边坡坡高的增加对位移量的变化有一定的影响,但对其整体变形破坏模式的影响不大。

5 反倾层状岩质边坡结构敏感性分析

5.1 倾角-位移敏感性分析

以倾角65°为基准,考虑岩层倾角变化对边坡位移变化增量的影响。取45°～85°共9组(每隔5°)倾角进行分析,建立边坡总位移敏感性关系。图6为不同岩层倾角下边坡变形位移敏感分析图。

图6 倾角-位移敏感性分析

由图6可知,岩层倾角的变化对边坡变形破坏影响显著。岩层倾角45°时,其位移量最小,并随着倾角增大而增大;在岩层倾角较大时,边坡位移量明显增加,但此时边坡位移增长幅度略有下降;边坡位移增量变化在-1.6～0.65的区间内,其最大值为0.65,最小值为-1.6,表明岩层倾角的变化使位移量发生变化显著。因此,可以推测岩层倾角变化对该类边坡变形破坏模式影响较大。

5.2 坡角-位移敏感性分析

图7为不同坡角下边坡变形位移敏感分析图。

图7 坡角-位移敏感分析

由图7可知,边坡位移随坡角的增大而增大。坡角靠近两侧边界时,边坡位移量增幅显著增大,各监测点的变化呈现出相似的变形趋势,表明坡角的增大导致岩层弯曲程度提高,边坡几何形态发生变化,弯曲倾倒变形现象更为明显。边坡位移增量变化在-2.9～4.5的区间内,其最大值为4.5,最小值为-2.9,表明坡角的变化使位移量发生变化显著。因此,可以推测边坡坡角变化对该类边坡变形破坏模式影响较大。

5.3 坡高-位移敏感性分析

图8为不同坡高下边坡变形位移敏感分析图。

图8 不同坡高下边坡变形位移敏感分析

由图8可知,边坡高度的增加会导致边坡折线深度增加,进而导致边坡变形位移量增大。当坡高位于50～100m范围时,其位移变化率为-1.5～1.1。因此可知坡高变化对位移量有部分影响,但对边坡破坏形式的变化基本无影响。

6 结 论

本文通过对反倾层状岩质边坡变形破坏影响因素进行研究,基于离散元UDEC数值模拟方法,建立简化二维数值模型并布设相应监测点位,得出影响反倾层状岩质边坡破坏的基本要素,并对边坡结构敏感性进行定量分析。结论如下:

1)边坡变形位移量随着岩层倾角、坡角、坡高的增大而增大,边坡结构-最大位移量曲线的变化趋势基本相同。

2)坡高的增加会导致岩层折断深度增大,但变形破坏模式基本不变。

3)坡角的增大导致岩层弯曲程度提高,边坡几何形态发生变化,弯曲倾倒变形现象更为明显。

4)岩层倾角、坡角的变化对边坡变形破坏有显著影响。