基于车联网数据的坡度预测研究

叶 宇，范超群，陈华晟，桑海浪，邓小超，潘明章

（1.广西玉柴机器股份有限公司，广西 玉林 537005；2.玉柴芯蓝新能源动力科技有限公司，广西 南宁 530000；3.广西大学机械工程学院，广西 南宁 530004）

0 引言

道路坡度是影响车辆行驶过程中纵向动力学控制的重要参数之一，对于重心高的车辆，在车辆控制中不考虑坡度的影响，可能会造成错误的车辆控制策略并导致事故发生[1]。其中，运动学方法常用于坡度估计，采用车载GPS 信息及大气压力信息可在不增加其余传感器的情况下对坡度进行估计[2，3]。

目前，LSTM 模型在车辆速度预测、车辆自适应巡航控制等方面研究中具有良好的使用效果，其在长期和短期的预测效果中具有一定的可靠性。利用车速和GPS 信息对坡度进行估计，并搭建基于LSTM 的坡度预测模型以对坡度进行预测，最后采用了自然驾驶数据对模型可靠性进行了评估。

1 坡度估计方法

根据CAN 总线收集的车速和GPS 高程信息进行坡度计算，计算式（1）-（2）。在角度较小时有：

其中H为GPS 高程，S为车辆实际行驶路程，L为GPS 高程间直线距离。则坡度可表示为：

其中△t为从高程H1行驶到高程H2所用时间，v1，v2分别为在高程和处车速。

由式（2）可知，GPS 高程与车速是确定坡度的重要影响因素，在实际数据采集过程中，可能存在数据丢失或异常的情况。针对海拔数据缺失或异常的情况，采用如图1 流程进行海拔修复。对于车速来说，当车辆处于停车状态时（v= 0），其GPS 高程应保持不变，故其坡度保持不变，当前位置的坡度采用相近的合理值进行填充。在车速数据异常状态下，采用线性插值法进行修正。

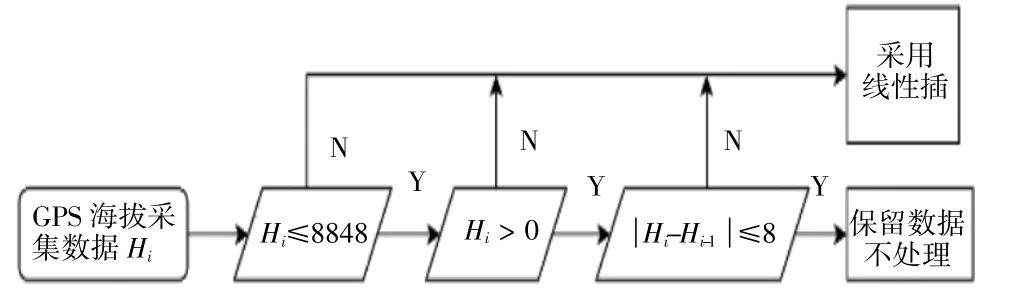
图1 GPS 海拔高度修复流程

1.1 基于LSTM 的坡度预测模型

递归神经网络（RNN）是一种特殊类型的神经网络，对于处理序列数具有良好的适应效果。其基本原理是该神经网络会对先前的信息进行存储，并应用在当前输出的计算中即当前神经元的输出不仅来自于当前神经元的输入，也包含了来自以往神经元的输出。与一般神经网络结构类似，RNN 的结构仍由输入层、隐藏层和输出层组成，图2 展示了RNN 在隐藏层中的各层间的反馈情况。

图2 RNN 隐藏层示意

在RNN 的学习过程中，长距离信息仍被保留故其学习能力会随着时间的推移而下降。在长短期记忆模型[4]（Long short-term memory，LSTM）中，隐藏层采用包括输入门、输出门和遗忘门在内的存储模块使得信息得以更新，从而避免RNN 保留大量的输入信息。针对所采用的基于实时车速和GPS 海拔高度的坡度计算方法具有良好的适用性。LSTM 能根据记忆模块对历史数据的训练，综合误差能够有选择地丢弃或增加信息，形成对历史数据的长期记忆，从而获得数据特征，构建训练模型。

“门”是LSTM 特有的控制信息选择性通过的逻辑结构，每个“门”的功能不同，其所采用的计算式也不同，LSTM 中隐藏层的基本结构如图3 所示。

图3 LSTM 隐藏层基本结构

根据每个“门”中不同的功能，其计算方法及传递内容有：

（1）遗忘门内采用式（3）进行计算

其中，xt是当前层的输入值，ht-1是上一层的输出，Wf是遗忘门的权重矩阵，σ为sigmoid 函数，bf为偏置项也称作误差项。在遗忘门内ft的结果可当作是信息被遗忘的概率，并将结果储存到遗忘门的结果xt处。在遗忘门中，主要判断信息被丢弃的程度。

（2）输入门内采用式（4）～（6）进行计算

该运算中将利用Sigmoid 函数和tanh 函数共同控制所加入的新信息。tanh 函数产生一个新的候选向量，以控制所加入的信息的量。

（3）输出门采用式（7）-（8）进行计算

该运算运用Sigmoid 函数确定输出信息的总量后再采用tanh 函数控制输出的信息中被过滤掉的信息的量，最终得到该层所有的输出信息。

1.2 模型准确性评估

为了保证预测结果一定的准确性，采用下述两个指标来对坡度预测模型进行评价。

（1）平均绝对误差（MAE）

其中，xi为原始数据值，下同。pi为利用坡度预测模型进行预测的结果值，下同。

该指标能直观反应预测值与实际值的偏差，其单位与预测值或真实值相同，该数值越小说明预测结果越准确。

（2）均方根误差（RMSE）

该指标计算的是预测值和实际值对应样本点的误差的平方和的均值，该数值越小说明预测结果越准确。

1.3 模型训练

根据坡度计算所采的方法中利用所采集的车速和GPS 海拔高度具有较强的时序性特征，构建基于LSTM 的坡度预测模型，该模型的训练具体过程为：

（1）坡度数据计算及预处理。对计算的坡度数据进行错漏筛查，并采用插值法对数据进行更正。

（2）对原始数据进行归一化处理，以此作为LSTM模型训练的输入。

（3）确定模型结构及参数。通过预训练确定模型所含的输入层、隐藏层和输出层的数目。并确定激励函数、神经元数目、损失函数、批处理数目、迭代次数等参数。

（4）初始化权重矩阵。采用随机数进行初始化。

（5）将完成归一化的坡度数据导入至输入层，由激活函数得到该层的输出结果。

（6）将（5）的输出结果及上一时刻的神经元状态值一同输入至LSTM 模块，经过该模块后，获得该隐藏层的输出结果，将其作为下一个隐藏层的输入之一，并重复该步骤直到遍历所有的隐藏层。

（7）将完成（6）的输出结果进行输出，该结果即为该时刻的坡度预测结果。

（8）将数据降至一维后经过输出层，并进行反归一化，得到与原始数据数量级相同的预测值后输出最终结果。

2 实例验证

利用一半挂车自然行驶数据共40379 条作为基于LSTM 坡度预测模型的验证数据集。在数据收集过程中，其海拔信息易于丢失，故在采用线性插值的方法对GPS 海拔高度进行修复，GPS 海拔及计算坡度数据修复示意如图4 及图5 所示。

图4 GPS 海拔高度修复示意图

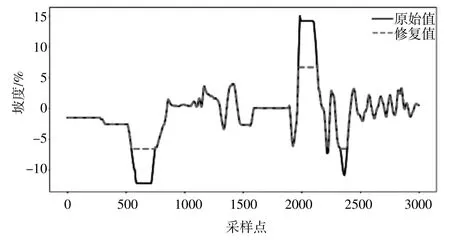
图5 坡度修复示意图

根据上述算法，在预训练过程中考虑到对数据预测准确性的要求，采用1 个输入层、1 个LSTM 和1 个输出层的网络结构。LSTM 层神经元数目在数据上表现为矩阵形式及矩阵维度，其数目的确定并没有固定值，通过多次模拟结果确定为16，同时确定采用epoch 的数目为50 既能满足准确性要求又能又比较高的训练效率。对于激活函数，采用sigmoid 函数和tanh 函数能够满足LSTM 模型中的输入和输出的要求。损失函数采用MSE 函数，不仅能满足模型输出的要求也能对该模型对交通流预测的适用性进行评价。优化函数采用adam，该函数是RNN 模型中常用的优化函数，LSTM 作为RNN 的一种，采用该函数能对梯度下降具有良好的适应效果。在模型验证过程中，所采用的训练集和测试集比例为1∶5。

经过模型训练，采用提出的基于LSTM 的坡度预测模型，对测试集数据进行验证，如图6 所示。各个评价指标如表所示。采用提出的新模型，其平均绝对误差为3.38，均方根误差为16.71。在预测结果方面具有良好的可靠性。

图6 LSTM 的坡度预测模型预测结果

为了进一步验证LSTM 的对坡度预测精度良，本选择其他神经网络对该序列进行预测。RNN（Recurrent Neural Networks）循环神经网络是LSTM的基础形式，其隐藏层内部结构简单各单元以长条状紧密结合并按时间序列发展方向递归最终形成闭环，由于参数的共享性处理时间序列数据时体现出一定的优势但是一旦序列过长无法避免出现梯度消失或梯度爆炸问题，因此成为其主要缺陷。GRU（Gated Recurrent Unit，GRU）是LSTM 模型的一种变体形式，与LSTM 模型主要区别在于该模型隐藏层仅有2个门即更新门和重置门，更新门主要发挥数据输入功能，控制上一时刻的信息带入到下一时刻的程度。重置门主要发挥数据丢弃功能，控制丢弃上一时刻的信息的程度。另外，GRU 将不产生表达内部状态的候选向量，故该模型计算过程与LSTM 相比较为简单。采用的RNN、GRU 模型与LSTM 模型结构类似，由1 个输入层、1 个隐藏层、1 个输出层组成，层间门控循环单元数均为16。如图7 为利用不同神经网络模型的预测结果。

图7 不同神经网络模型坡度预测结果

根据预测结果计算对应的平均绝对误差及均方根误差如表1 所示，可以看出，由于GRU 的本质是将LSTM 中的遗忘门和输入门整合为更新门，故其预测结果精度与LSTM 类似。对于RNN 来说，由于其自身对长期依赖的处理过程中的固有缺陷，故其表现不如GRU 或者LSTM。

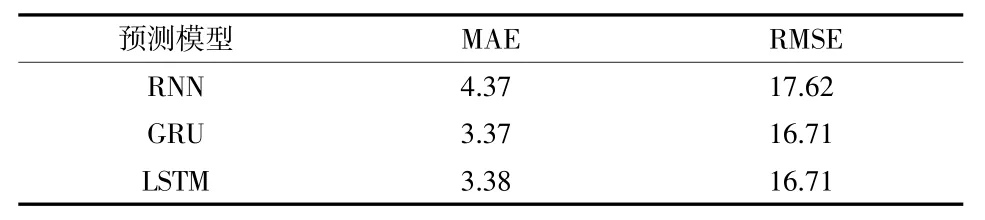
表1 三种模型预测精度对比

3 结语

利用车速和GPS 海拔高度信息对车辆所处行驶环境的坡度进行了估计。为对道路坡度进行预测，搭建了基于LSTM 的坡度预测模型，并对坡度进行了预测，预测误差较低。验证了基于LSTM 模型的坡度预测的适用性，此外，利用LSTM 的预测结果与GRU、RNN 进行对比，表现为LSTM 在坡度预测方面相较于其他神经网络具有更高的精度。