基于优化MCMC算法的地震弹性阻抗反演方法
2023-08-23郭淑文金凤鸣韩国猛国春香周淑慧
赵 晨, 郭淑文, 金凤鸣, 韩国猛,于 超, 邢 兴, 国春香, 周淑慧
(中国石油大港油田公司,天津 300280)
0 引言
物探技术是实现油气田勘探的重要手段,主要分为重力勘探、电法勘探、磁法勘探以及地震勘探等。其中地震勘探技术是解决油气勘探问题最为广泛、有效的方法。当前,石油勘探已从简单的构造识别转向复杂构造、薄储层的识别,储层埋藏深,且地下构造较为复杂,以地震反演为核心的地震物探技术可以充分利用地震数据在整个三维空间的振幅以及相位特征,实现地下储层参数的有效预测。在地震反演过程中,选取合适的储层敏感参数对于储层识别来说是极其重要的。传统的叠后反演仅能反演纵波阻抗信息,难以预测较为复杂的储层[1],而弹性阻抗反演利用叠前角度部分叠加道集进行反演,即提高了反演的稳定性,又可以直接反演得到拉梅参数、纵波模量和流体因子等其他反映岩性和流体信息的储层参数[2]。1999年,Connolly[3]首次提出了弹性阻抗的概念,并给出了弹性阻抗方程。Whitcombe[4]对Connolly弹性阻抗方程进行了标准化处理。弹性阻抗反演采用叠前角度部分叠加道集,具有较强的抗噪能力。
与传统的确定性反演方法相比,随机反演对于具有薄层特征的优质储层的识别具有一定优势[5-6]。随机地震反演方法是以地质统计学为基础,其技术关键在于分析并拟合储层地球物理特性的分布规律,并对不同地球物理参数进行研究,以获得这些参数与地层岩性的关系[7]。由于随机反演方法可以同时满足实际地震观测数据和测井数据,且可以有效地利用测井数据中所包含的高频信息提高反演的分辨率[8-9],因此其具有较为重要的实际意义。
马尔科夫链蒙特卡洛方法(MCMC)是主要的随机反演方法之一,其可以提供反演参数后验概率密度的一系列样本[10],通过对这些样本进行统计分析,可以获得满足要求的反演结果。基于Metropolis算法[11],Hasting[12]提出了Metropolis-Hastings(MH)算法,这是最常见的MCMC方法;Alberto等[13-14]采用基于贝叶斯理论的Metropolis-Hastings算法来估计饱和度前缘的位置,并研究了该问题的不确定性;Tiancong Hong等[15]提出基于马尔科夫链蒙特卡洛算法的Multi-scale GA方法,提高了计算效率以及估值精度。Chen等[16]发现MCMC反演方法能提供大量与未知参数有关的全局信息,与确定性反演方法相比,能得到更好的估计值;王丹阳等[17]研究了基于MCMC方法的叠后及叠前地震反演方法;潘新朋等[18-19]将AM策略与DR策略相结合,提出了AMDR-MCMC算法,将DR策略融入AM策略,克服AM策略过度依赖初始协方差的劣势。
综合前人研究成果,可以发现传统的MCMC算法较为依赖初始模型及搜索策略,当计算时间有限或搜索策略设置不当时,对于一个较为复杂的参数空间, MCMC算法往往不能对反演参数空间进行充分的搜索[20],且收敛速度较慢。这是由于在反演初期,接受概率略大,导致许多不必要接受的状态得到了接受,使得前期的马尔科夫链产生了较大偏差。针对该问题,笔者引入一个逐渐减小的变量来调整状态接受的概率,提高算法的稳定性和收敛性。本文对传统的MCMC算法的接受概率表达式进行了改进,提出了新的优化MCMC算法,并将其应用于叠前弹性阻抗反演中,利用测井信息获得多个角度弹性阻抗的先验信息,利用角度叠加数据及正演关系获得似然函数,并添加反射系数约束信息,可以提高反演的可靠性。
1 基于优化MCMC算法的弹性阻抗反演方法
1.1 MCMC算法
MCMC方法的核心是构造一个平稳分布且与所求后验分布相同的马尔科夫链,反复迭代至平稳状态,从而得到后验分布的样本,再基于这些样本计算统计参数[21]。
其主要步骤:首先由建议分布q(xt,x*),产生一个潜在的转移xt→x*,然后根据概率α(xt,x*)来决定是否接受。从[0,1]的均匀分布上抽取随机数u,则马尔科夫链下一时刻的状态为[22]
(1)
式中:t表示马尔科夫链的当前时刻;xt表示在t时刻的值;x*表示由建议分布产生的候选抽样值;α(xt,x*)代表转移核函数,常用的形式为
(2)
当目标分布取为似然函数L(x),且建议分布为对称分布时,则式(2)可改写为
(3)
因此,对于反演问题,MCMC算法的接受概率可改写为
α(xt,x*)=exp{min[0,J(x*)-J(xt)]}
(4)
式中:J表示所构建的目标函数。
经过多次迭代,可以获得后验概率分布的一系列样本,对这些样本进行筛选,可获得满足要求的反演结果。
1.2 优化MCMC算法
MCMC算法属于蒙特卡洛算法,MCMC算法通过对先验分布进行抽样得到新的样本,可获得收敛于后验概率分布的一系列反演结果的样本,因此可以对反演结果进行不确定性分析。
参照式(6),引入一个逐渐减小的变量,可将式(4)改写为
(5)
式中:φ是一个随着迭代次数增加而逐渐趋近于0的正变量,将其称为衰减函数,其具体形式如下:
φ=φ0q
(6)
式中:φ0为上次迭代的衰减函数值,q为衰减因子,一般取为[0,1]的常数。
φ0取值大小与算法在运算过程中的目标函数值之差有关,一般可以选取算法运算过程中较大的目标函数值之差,使算法在前期阶段快速收敛,其与算法收敛速度有着较为密切的关系。q的取值控制着φ衰减的速度,其需要确保当解收敛到真值附近时,φ的取值已对接受概率影响不大。
衰减函数值对于接受概率来说,起到了一个调节的作用,其主要发挥作用在算法前期,该阶段解与真实值差距较大,而φ的存在可以使解更加快速的收敛到真值附近。后期φ对算法几乎没有影响,因此确保了平衡状态下对后验概率的采样。对于优化MCMC算法来说,φ的引入可以适当减少当前状态的不必要的转移,使马尔科夫链能够更加快速、稳定地收敛于后验概率密度。
参照传统的MCMC算法,给出优化MCMC算法的实现流程(图1),图中rand为0到1之间的随机数。其与MCMC算法的主要区别在于优化MCMC算法采用了新的接受概率表达形式。

图1 优化MCMC算法流程图
1.3 弹性阻抗反演方法
在本文研究工区,纵波模量可以较好地识别优质储层,因此笔者利用基于纵波模量的弹性阻抗方程来实现弹性阻抗反演。
基于Connolly弹性阻抗公式,宗兆云等[23]改用纵波模量M,剪切模量μ,密度ρ来表示Connolly弹性阻抗方程:
(7)
式中:Ie表示计算的弹性阻抗,M0、μ0、ρ0分别表示纵波模量、剪切模量和密度的平均值。
参数a、b、c的取值:
b=-4ksin2θ,
由不同角度的地震数据,反演可以得到相应的弹性阻抗体,利用井旁道弹性阻抗反演结果及测井数据,即可得到纵波模量等弹性参数的信息[24-25]。
贝叶斯理论框架下的随机反演方法可以更好地融合地震数据和测井信息[26]。利用贝叶斯理论,可有效地提高算法的精度及可靠性。
贝叶斯公式具体形式为
p(m)p(d|m)
(8)
式中:d表示实际地震记录;p(m)为弹性阻抗模型m的先验概率密度;p(d|m)为似然函数;p(m|d)为弹性阻抗模型m的后验概率密度。
(9)
式中:g表示正演算子,N表示实际地震数据的采样点数量。
假设反演的弹性阻抗模型满足高斯分布的形式,故模型参数的先验概率可表示为
(10)
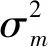
将式(12)、式(13)代入式(11)中,取对数,并加入反射系数约束项,即可获得目标函数形式:
(11)

2 模型试算
首先利用一维模型进行反演测试,该一维模型来自某井资料。利用弹性阻抗方程,合成7°、18°、26°三个角度的弹性阻抗模型,并将模型与25 Hz的雷克子波褶积正演合成三个角度的地震道集,得到未加噪声的观测地震记录。分别利用不同的反演算法进行反演测试,并针对反演精度、抗噪性、收敛能力与收敛速度等方面,进行对比分析。
2.1 反演精度
在相同搜索策略下,分别利用优化MCMC算法与传统MCMC算法进行一维模型测试,初始模型为平滑模型。图2为未加噪声时MCMC算法反演结果与模型数据的对比,图3为在相同搜索策略下未加噪声时优化MCMC算法反演结果与模型数据的对比,可以发现当搜索策略相同时,优化MCMC算法与MCMC算法均能获得较好的反演结果,且前者精度要略高于后者。

图2 初始模型为平滑模型且未加噪声时MCMC算法小角度(a)、中角度(b)、大角度(c)弹性阻抗反演结果及所提取的纵波模量(d)结果与模型数据的对比
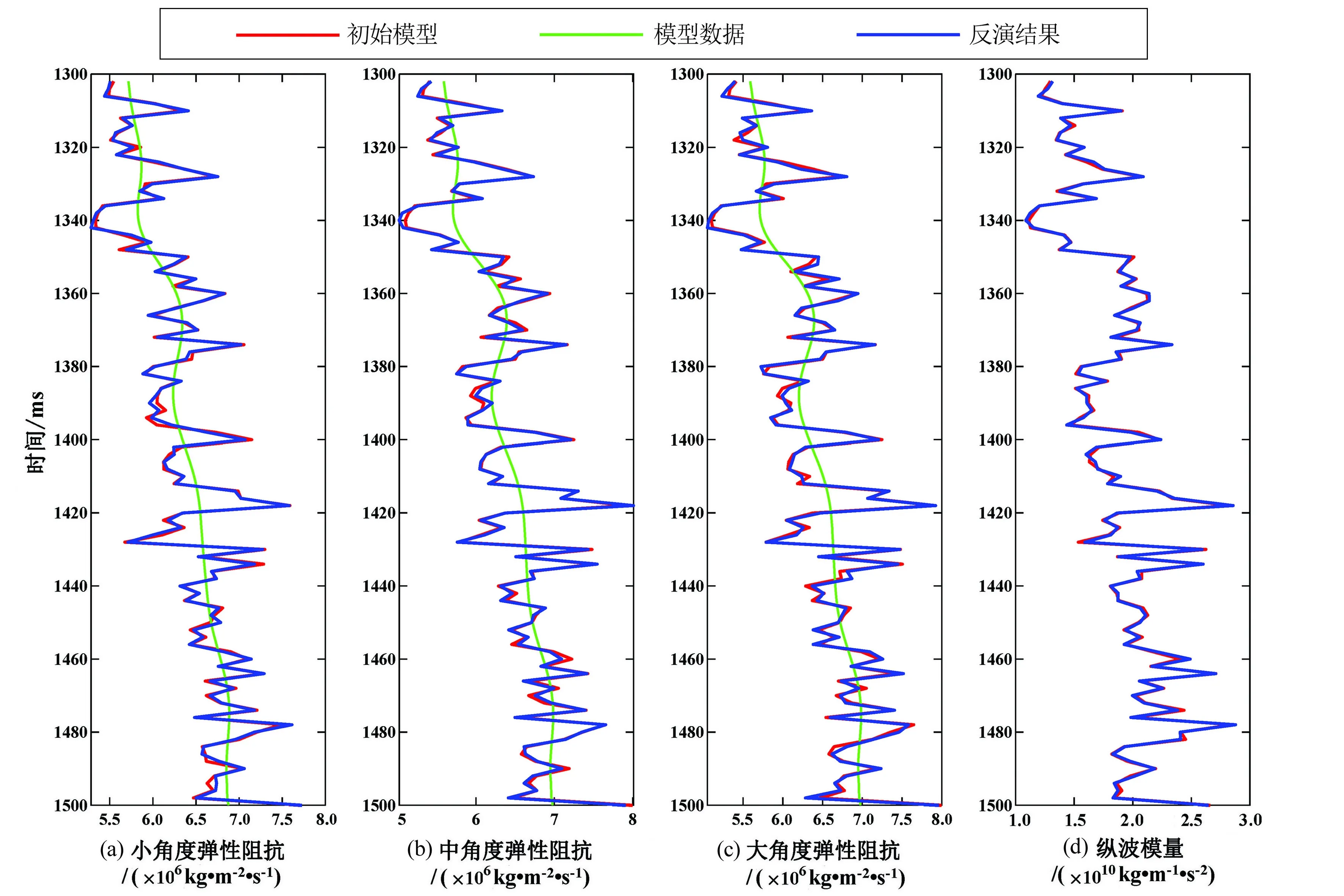
图3 初始模型为平滑模型且未加噪声时优化MCMC算法小角度(a)、中角度(b)、大角度(c)弹性阻抗反演结果及所提取的纵波模量(d)结果与模型数据的对比
2.2 抗噪性
为了验证算法的抗噪性,在正演合成的地震道集中添加信噪比为3的高斯随机噪声生成含噪观测地震记录。图4为信噪比为3时优化MCMC算法反演结果与模型数据的对比。对比图3与图4,可以发现,存在噪声时,反演依旧可以取得较好的结果,说明该方法具有一定的抗噪性。
图4 初始模型为平滑模型且信噪比为3时优化MCMC算法小角度(a)、中角度(b)、大角度(c)弹性阻抗反演结果及所提取的纵波模量(d)结果与模型数据的对比
2.3 收敛能力
将初始模型改为均匀模型,分析当初始模型与真实模型相差较大时,对MCMC算法的影响。图5为初始模型为均匀模型下MCMC算法反演结果与模型数据的对比,图6为相同初始模型下优化MCMC算法反演结果与模型数据的对比。可以发现两者依旧可以取得较好的反演结果,说明即使初始模型与真实模型具有较大差距时,两种算法依然可以有效收敛,两种算法均具有较强的收敛能力。

图5 初始模型为随机模型且未加噪声时MCMC算法小角度(a)、中角度(b)、大角度(c)弹性阻抗反演结果及所提取的纵波模量(d)结果与模型数据的对比

图6 初始模型为随机模型且未加噪声时优化MCMC算法小角度(a)、中角度(b)、大角度(c)弹性阻抗反演结果及所提取的纵波模量(d)结果与模型数据的对比
2.4 收敛速度
从中角度弹性阻抗模型中选取某一位置处的采样点,比较两种方法在该采样点处的弹性阻抗值随迭代次数的变化。图7为初始模型分别为平滑模型和均匀模型时利用MCMC算法和优化MCMC算法在某采样点的阻抗值随迭代次数的变化曲线。由图4可以发现,当初始模型为平滑模型时,MCMC算法在迭代到60 000次左右才开始在真值附近区域内采样,共耗时31.1 s,而优化MCMC算法在5000次左右就开始在真值附近区域内采样,共耗时4.1 s,且后者的稳定性要由于前者;当初始模型为均匀模型时,MCMC算法在迭代到75 000次左右才开始在真值附近区域内采样,共耗时37.1 s,而优化MCMC算法在13 000次左右就开始在真值附近区域内采样,共耗时6.8 s。这说明优化MCMC算法相比传统的MCMC算法具有更高的计算效率,且反演结果更加稳定,且当初始模型较差时,依然可以较快的收敛。这是由于φ的引入可以适当减少当前状态的不必要的转移,使马尔科夫链能够更加快速、稳定地收敛于后验概率密度。

图7 不同初始模型及不同方法下的中角度弹性阻抗值随迭代次数的变化
对于衰减函数,初始值φ0与算法的收敛速度有着较为密切的关系,其越大,算法初始阶段收敛速度就越快,而衰减因子控制着衰减函数的衰减速率,其要保证在算法到达平衡状态之前,衰减函数值对于算法在平稳状态下的采样不再有明显的影响。
图8为初始值为6时不同衰减因子的衰减函数值随迭代次数的变化和MCMC算法及优化MCMC算法中角度弹性阻抗目标函数值随迭代次数的变化。此时,初始模型选择的是随机模型,且未加噪声。

图8 中角度弹性阻抗目标函数绝对值随迭代次数的变化(a)与衰减函数值随迭代次数变化(b)
衰减因子需要确保当解收敛到真值附近时,φ的取值已对接受概率影响不大。由图8可知,优化MCMC算法在迭代10 000以后,才会到达平稳状态。而当衰减因子为0.9时,衰减函数值在10 000次左右时已可忽略不计,说明该取值是可以接受的,且能充分发挥算法的优势。前面优化MCMC算法反演均采用了初始值为6,衰减因子为0.9的设定。
图9为某采样点小角度、中角度及大角度弹性阻抗后验概率分布的样本直方图,可以发现其均满足高斯分布的形式,与先验假设相一致,因此,选取平均值作为其反演结果。
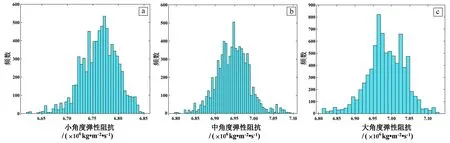
图9 某采样点小角度(a)、中角度(b)及大角度(c)弹性阻抗概率密度直方图
3 实际资料处理
为了测试该方法在实际资料应用中的可行性,笔者对某工区实际资料进行反演测试。该资料来自某海上工区。该工区发育低渗储层,储层内部变化规律复杂,非均质性很强。经过岩石物理分析表明,纵波模量可以较好地分辨优质储层(图10)。

图10 A井纵波模量与体积模量交会图
为了提高反演的计算效率,将地震偏移距道集叠加为2°~12°、10°~20°、18°~30°三个角度部分叠加的地震剖面,并从角度叠加数据中提取子波,利用优化MCMC算法进行反演。
图11为弹性阻抗反演结果,可见反演结果与测井数据吻合较好。图12为中角度部分叠加实际地震数据与中角度弹性阻抗反演结果所合成的地震记录的对比,可以发现合成地震记录与实际地震记录较为吻合。图13为MCMC算法及优化MCMC算法目标函数值随迭代次数变化,可以发现优化MCMC算法相比MCMC算法能更加快速的收敛,说明了该算法的优势。
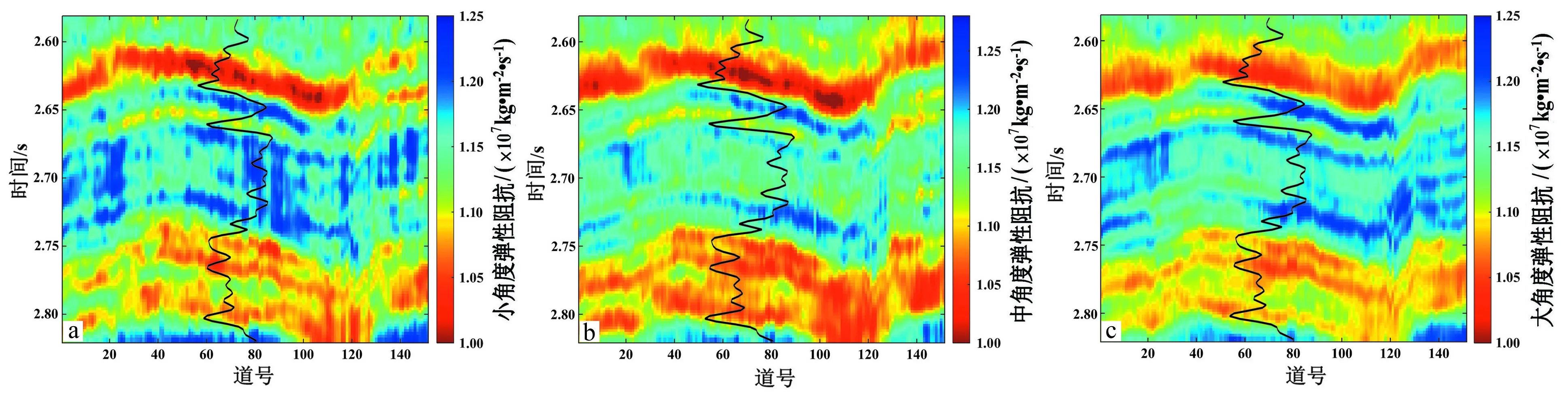
图11 小角度(a)、中角度(b)及大角度(c)弹性阻抗反演结果
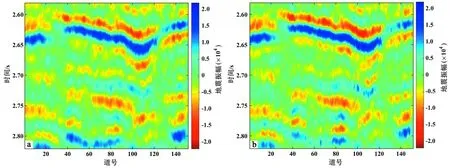
图12 中角度部分叠加实际地震数据(a)与中角度弹性阻抗反演结果所合成的地震数据(b)的对比
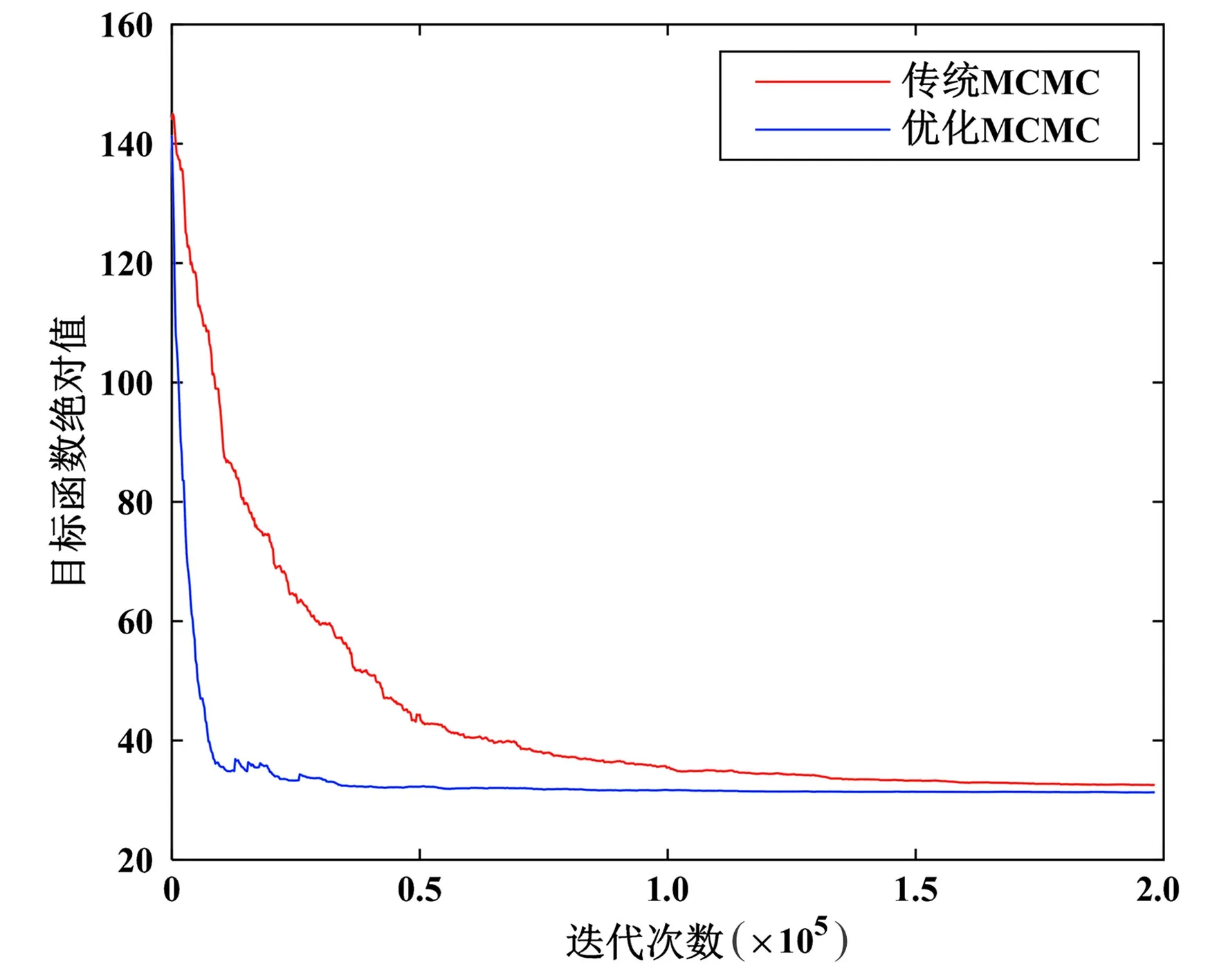
图13 MCMC算法及优化算法中角度弹性阻抗目标函数绝对值随迭代次数的变化
图14为基于优化MCMC算法反演获得纵波模量反演结果与确定性反演所得到纵波模量反演结果的对比,可以发现前者可以很好地指示优质储层的位置,且具有较高的分辨率。因此基于优化MCMC算法弹性阻抗反演方法可以很好地应用于实际工区的纵波模量预测之中。
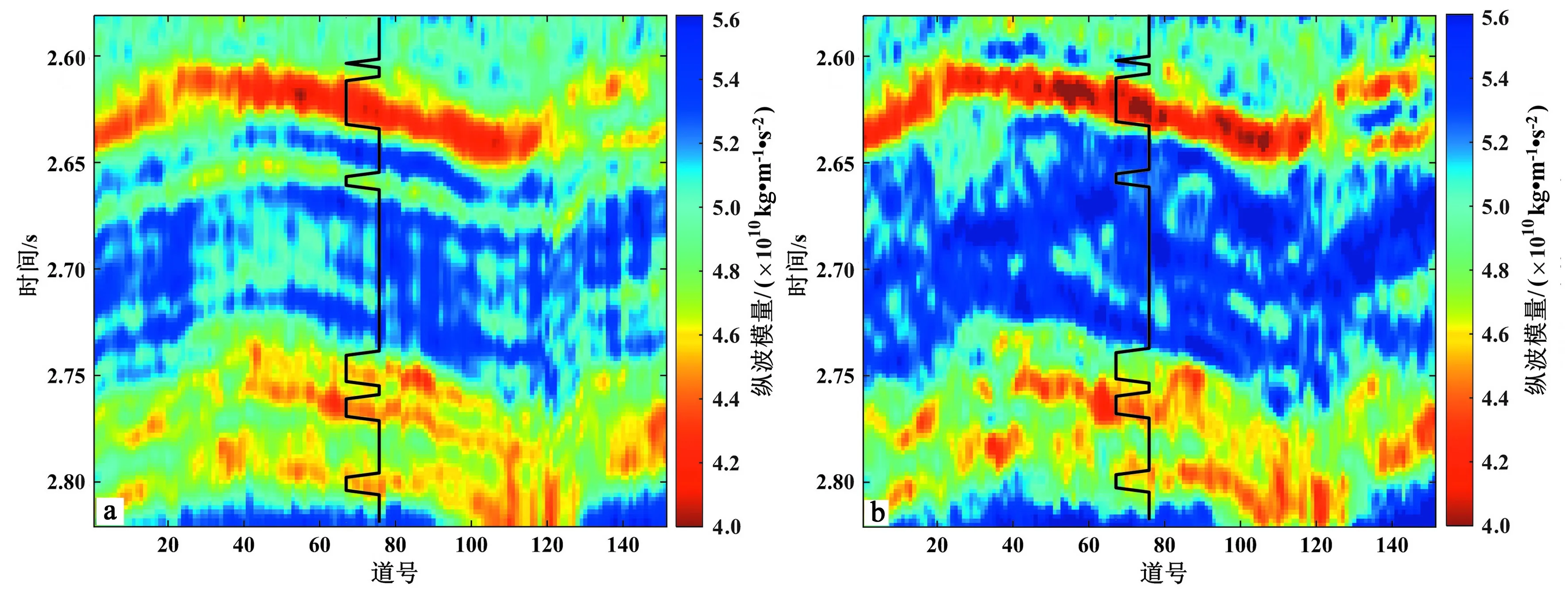
图14 基于优化MCMC算法反演获得纵波模量反演结果(a)与确定性反演所得到纵波模量反演结果(b)的对比
5 结论
本文对传统的MCMC算法的接受概率表达式进行了改进,提出了新的优化MCMC算法,并将其应用于叠前弹性阻抗反演中,通过模型测试与实际数据应用,可以得出以下结论:
(1)在反演精度及收敛速度方面,优化MCMC算法通过引入衰减函数,有效减少了算法前期不必要的状态转移,使马尔科夫链能够更加快速、稳定地收敛,提高了算法的精度和收敛速度。
(2)在抗噪性及收敛性方面,优化MCMC算法在地震记录噪声较高或初始模型与真实模型差距较大的情况下,依然可以取得较好的反演结果,说明算法具有一定的抗噪性并具备较强的收敛能力。
(3)通过实际数据应用,可以发现基于优化MCMC算法的纵波模量弹性阻抗反演方法相比传统的稀疏约束脉冲反演方法,具有更高的分辨率。
