基于Adagrad算法的LMS步长优化

陈智国，王忠策

（1.吉林化工学院 信息与控制工程学院，吉林吉林，132022；2.吉林农业科技学院 电气与信息控制工程学院，吉林吉林， 132101）

0 引言

自适应了滤波算法是信号处理中重要的组成部分[1]，广泛的应用与系统的辨识、消除回波、自适应谱线增强、自适应信道均衡、语音线性预测、自适应天线阵等诸多领域当中。LMS算法是最小均方算法的简称英文全称为Least Mean Square，算法以其实现方便，性能稳定而闻名。LMS算法通过不断更新滤波系数来实现多阶单位冲击响应滤波器。

Adagrad算法是梯度下降的算法在近些年发展起来，Adadrad的优点就是它没有了手动调试学习率的方式，转变为在算法迭代的过程中自己不断调整学习率，从而让期望函数中每一个参数都拥有学习率。

针对LMS算法中收敛速度比较慢、滤波中误差较大的问题，在LMS算法中引入了Adagrad算法来改变LMS算法固定步长。

1 LMS自适应滤波器

LMS算法最先是由美国斯坦福大学的Widrow和Hoff在20世纪中期研究自适应理论模型时率先研究提出，因为LMS算法的工作计算量小，容易实现等优点被广泛地应用于雷达、通信、医药、图像处理等多个领域[2]。LMS算法不需要知道输入的信号与所期望的信号的一些特征情况，而在某一时刻的权重系数是通过上一时刻的权重系数加上负均方误差梯度与比例项的积来计算得到。自适应滤波的基本结构如图1所示，其中内部LMS算法矢量图如图2所示。其中x(n)为滤波器输入的信号，y(n)是由滤波器计算后输出的信号，d(n)是系统期望的信号，e(n)是系统接收期望的信号与输出信号之间的误差值，w(n)是权向量。

图1 自适应滤波器结构图

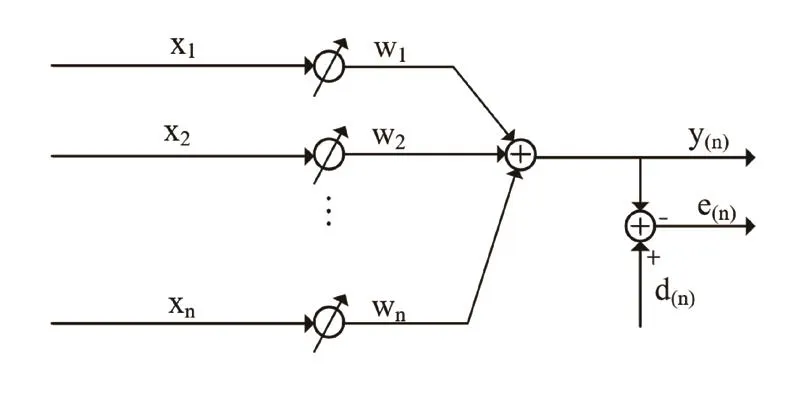
图2 算法矢量图

LMS算法一般步骤如下[3]：

（1）初始化信号的权重系数；

（2）计算与输入信号相对应的输出信号；

（3）输出信号与期望信号之间的误差值计算；

（4）自适应滤波器权重系数的迭代及更新。

算法不断迭代权重系数，直到收敛。为了结果的收敛性步长因子μ因满足一定的条件限制即：0＜μ＜1λmax。

其中λmax为输入信号自相关矩阵最大的特征值。由于LMS算法中的步长为固定值，那么LMS算法的收敛速度和稳态误差之间的矛盾会难以解决。当步长因子μ较小时算法的稳态误差会较小，但是此时的收敛速度也会比较慢。当步长因子μ较大时算法收敛速度则会变快，而此时的稳态误差这会增大[4]。所以为了使这个问题得到有效的解决，考虑了一些LMS算法的优化思路：（1）固定步长法：步长参数μ是一个常数，不随迭代次数变化。这种方法简单易实现，但是需要根据信号的特性选择合适的 值，否则会影响收敛速度和稳态误差。（2）变步长法：步长参数 是一个变化的量，随着迭代次数或者误差信号的大小而调整。这种方法可以提高收敛速度和降低稳态误差，但是需要增加计算量和复杂度。（3）自适应步长法：步长参数μ是一个自适应的量，根据滤波器系数的变化而调整。这种方法可以适应信号的非平稳性和噪声干扰，但是需要增加存储空间和计算量。这里选择自适应的步长优化方法在LMS算法中引入一种深度学习Adagrad算法来对步长μ进行合理的优化处理，从而实现加快收敛同时减少稳态误差的两重效果。

2 深度学习Adagrad算法

Adagrad算法全称：Adaptive Gradient是2011年由Duchi提出来的一种学习速率自适应梯度下降算法，是梯度下降优化算法的扩展，算法的核心思路就是，在算法迭代训练过程中学习效率是衰减的，如果一个算法它的下降梯度一直都比较大那么Adagrad算法便会降低这个梯度参数，防止过度的震荡减小稳态时的误差。Adagrad算法是一种基于梯度下降的优化算法，它能够自适应地调整每个维度的学习率，能够合适的处理二次优化等问题，能够有效地应对梯度下降算法难以处理的拉长的损失函数。LMS算法的主要缺点在于收敛速度慢，尤其是对于有噪声的收敛速度，其次是LMS算法需要选择合适的步长参数，对于非平稳的信号需要不断地调整步长参数，否则可能会导致不稳定或过度调整的情况。LMS算法中因为步长是固定值的原因，梯度下降总是固定值，所以造成收敛速度与稳态误差之间难以解决的矛盾。但是不同的情况所需的下降梯度也不同，算法进行的过程中又不能人工参与地改变算法参数，所以为了解决这个矛盾将Adagrad梯度下降优化算法引入到LMS算法中，达到自适应的梯度下降步长，首先是输入较大的步长，以此来加快算法的收敛速度，然后步长再逐渐地衰减来保证稳态误差减小，这样就实现了加速收敛和同时减少稳态误差的双重效果。Adadrad算法的迭代更新过程如下：

（1）计算目标函数当前的参数梯度gt；

（2）根据以及知道的梯度计算一阶动量mt，二阶动量vt；

（3）计算当下时刻的学习率；

（4）根据计算的下降梯度进行更新迭代优化。

Adagrad算法的优点在于在每次迭代更新的过程中都会把梯度记录下来，每一个梯度的学习效率不一样并且每个梯度都是在不断减小，在梯度大的维度中减小下降的速度，在梯度较小的维度中加快下降速度。

3 LMS算法的优化

■3.1 算法提出步长因子理论分析

首先定义权向量W=[w1,w2,w3···wn]T，误差信号式(3)中输出信号的矢量和形式可以表达为：

所以对误差函数的平方根可以得到如下形式：

对误差函数两边进行求数学期望，可得均方误差：

由此可见均方误差是权系数向量W的二次函数，它由一个中间向上的抛物曲面构成，所以它由唯一的最小值函数，调节权系数使均方误差最小，就相当于沿抛物面下降来找到最小值。所以可以用梯度法来求得最小值。式(10)两边对权系数W求导，可以得到均方误差函数的梯度[5]：

所以令Δ(n)=0，即可得到最佳的权系数向量。由此得到的最佳权系数向量精确，但是需要知道Rxx和Rxd的先验统计知识而且还需要进行矩阵的求逆运算，会增加很大的运算量，所以在LMS算法中根据最优化算法中的最速下降法，“下一时刻”权系数向量w(n+1)应等于“现在时刻”权系数向量w(n)加上一个负的误差梯度-Δ(n)的比例项来计算得到[6]，即：

式(12)中μ就是控制收敛速度与稳态误差的常数，即收敛因子步长。所以LMS算法中的两个关键便是梯度Δ(n)的计算与μ的选择。LMS算法中用到了一种十分有效的近似计算法求的Δ(n)，即用作为均方误差的估计再来计算得到：

■ 3.2 LMS算法步长优化

改进的算法通过在优化步骤中使用Adagrad中的自适应下降梯度的方式来代替LMS算法中的固定步长，最终改进的算法具有加速收敛和同时减少稳态误差的双重效果。根据公式(3)(4)(5)有以下优化：

其中r是误差平方和的累积，η是需要自己设置的初始学习率，α是为了维持数值稳定性而添加一个很小的常数，如10-6。由此可见，在算法迭代中随着误差函数的不断累计那么r值就在逐渐增加，分母在不断变大。所以整体步长μ是一个由大变小的过程，那么对应于收敛速度于稳态误差中的效果就是，初期步长大算法的收敛速度快随着误差平方根的累计r增大，分母增大步长减小那么收敛速度逐渐减小最后使得稳态误差减小。所以优化后的算法可以达到加速收敛和减小稳态误差的双重效果。改进后的LMS算法一般步骤如下：

（1）初始化滤波器：w(0)、x(0)；

（2）对于输入的样本信号x(n)计算输出信号y(n)；

（3）由期望信号d(n)与输出信号y(n)计算的误差值e(n)；

（4）将误差值函数进行累加计算；

（5）通过改进后的LMS算法进行滤波器示数w(n)；

（6）返回步骤（2）直到收敛结束。

利用Mtalab仿真进行仿真分析对比改进前后的收敛速度与稳态误差，其中输入信号为振幅为2的正弦函数如图3所示，加入的误差噪声信号为高斯白噪声信号如图4所示。图5、图6分别为LMS算法仿真结果和改进后的LMS算法仿真结果。

图3 输入信号

图4 高斯白噪声干扰信号

图5 LMS算法滤波结果

图6 改进后LMS算法滤波结果

由图5和图6可见LMS算法在迭代到100次的时候波形逐渐过滤掉噪声信号出现了原本期望得到的信号，而改进后的LMS算法在跌打到50次左右的时候就可以呈现出期望信号可见在收敛速度上改进后的LMS算法收敛速度更快。然后再对改进前后的LMS算法误差进行仿真分析结果如图7、图8所示。

图7 LMS算法误差

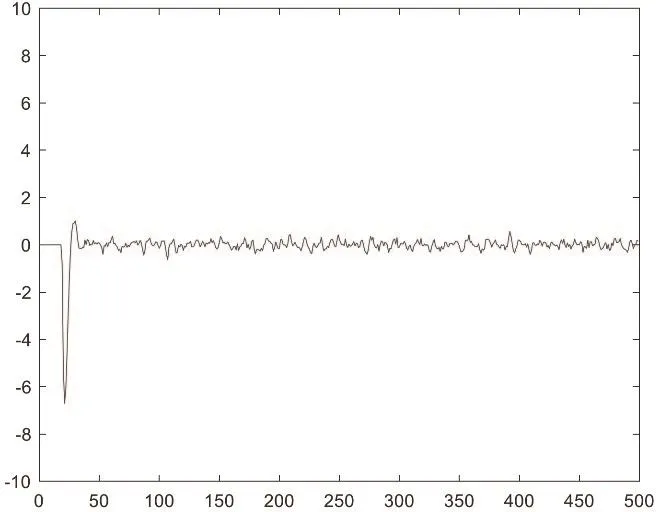
图8 改进LMS算法误差

收敛速度和稳态误差是判断LMS算法性能优劣的两个重要指标，在收敛速度方面改进后的LMS算法优于原本的LMS算法，在误差方面为了便于对比所以起始误差都设置为0起初两者误差还是相对较大的，但是随着迭代次数的增加可变步长LMS算法的优势就体现了出来随着步长值减小误差值也在不断减小，在迭代到50次左右的时候误差信号已经稳定在0上下波动，而原本的LMS算法因为固定步长的原因在迭代到100次左右的时候出现误差在0上下波动且波动幅度大于改进后的LMS算法。由此可见，在对LMS算法中固定步长的改进中将其与深度学习算法Adagrad算法中自适应学习率的方式相结合，可以实现使LMS算法加快收敛速度和减小稳态误差的双重效果。

4 结语

LMS算法是当前应用最广泛的自适应滤波算法之一，本文介绍了LMS算法以及算法优劣点，并且从深度学习Adagrad算法的角度对LMS算法的劣势固定步长做了优化，使改进后的算法比原本的算法在收敛速度方面更快在稳态误差方面更小。并且通过Matlab仿真验证。结果表明改进后算法收敛快误差小，满足了加速收敛和同时减少稳态误差的双重效果，能有效地提高滤波器滤波效果。