考虑初始含水率沿程不均匀分布的畦灌技术要素调控

李 江 黄增健 李 涛 缴锡云,2 史传萌 张状状

(1.河海大学农业科学与工程学院, 南京 210098; 2.河海大学水文水资源与水利工程国家重点实验室, 南京 210098)

0 引言

畦灌是常用的地面灌水方式之一,具有田间设施简单、运行成本低、易于实施等优点,同时也存在灌水质量不高的问题[1-2]。在畦灌过程中,土壤水分入渗与地表水流运动同时进行,两者密切联系、相互作用,共同影响灌水质量。田面坡降是畦田的自然特征,自然坡降使得灌溉水在重力及水流推动作用下从畦首顺坡降流向畦尾。在我国半干旱半湿润地区以及湿润地区,降雨亦会通过畦田的自然坡降发生入渗以及产生径流,若降雨历时过长或雨强过大,在封闭畦田的尾部还可能形成积水,降雨产流之后的畦田沿畦长方向会出现一定程度上的土壤水分分布不均匀现象[3]。土壤水分状态是影响土壤入渗性能以及农田作物耗水的重要因素,早期关于畦灌技术要素设计的相关研究表明土壤入渗的空间变异性对灌水质量的影响尤为显著[4-5]。因此,降雨产流所形成的土壤水分空间变异,将会通过影响土壤入渗性能进而影响畦灌水流运动特性,使得按一般情况设计的畦灌技术要素不能满足灌水质量最高的要求。

畦田规格、田面坡度、入畦流量、改水成数等灌水技术要素是影响畦灌灌水质量的重要因素[6-11],试验观测与模型模拟是研究不同技术要素控制条件下畦灌水流运动的有效手段。畦灌模型模拟可以减少试验次数,通过数值计算的方式很好地描述和再现畦灌水流运动过程,帮助学者对比大量预设灌水技术条件下的灌水质量,并从中推荐较优的灌水技术方案[12-15]。目前常用的畦灌模拟软件有WinSRFR和SIRMOD,二者被广泛地应用于解决不同单宽流量、改水成数、土壤特性、畦田规格等因素对于灌水质量的影响问题[2, 16-19]。针对土壤入渗性能的空间变异性,已有学者对不同土壤入渗性能条件下的畦灌灌水质量进行评价以及对灌水技术要素进行设计[20-22]。

然而,现有考虑土壤入渗性能空间变异性的研究多是将土壤入渗性能作为土壤的固定属性来进行统计上的分析,并且假定灌水前畦田土壤初始含水率为均匀的分布状态,很少考虑初始土壤水分空间变异性对于畦灌水流运动以及灌水质量的影响。降雨产流等因素导致的畦田土壤含水率分布不均匀,及其对畦田作物耗水强度、灌水前土壤入渗性能以及灌水质量的影响等相关问题还有待进一步探讨。因此,针对降雨产流后畦田土壤初始含水率沿程不均匀分布的情况,本研究开展一维土柱入渗试验、二维土槽灌溉试验,进一步结合WinSRFR地面灌溉模拟模型,探讨初始含水率沿程不均匀对畦灌田面水流运动和灌水质量的影响规律,优化求解畦灌技术要素,以期为土壤初始含水率沿程不均匀条件下畦灌技术要素调控提供科学依据。

1 材料与方法

本研究首先获取不同初始含水率条件下的入渗参数,进一步对畦田灌水技术要素进行调控。具体来说,开展一维土柱入渗试验,确定Koistiakov模型中入渗参数随初始含水率的变化关系式;同时,在土槽中开展含水率沿程不均匀条件下的畦灌试验,观测田面水流运动状况,利用拟合好的入渗参数随初始含水率变化的函数计算沿程入渗量,并对不同处理下的灌水质量进行评价;其次,将拟合的入渗参数随初始含水率的变化关系式代入WinSRFR模型,对土槽试验中的畦灌水流运动进行模拟,对比实测数据与模拟数据,对模型进行验证;最后,设置不同畦灌技术要素组合,利用验证好的WinsSRFR模型开展初始含水率沿程不均匀条件下的畦灌技术要素优化,最终针对由降雨产流导致的畦田水分不均匀状态,对畦灌技术要素进行调控。具体研究方法如图1所示。

1.1 不同初始含水率条件下入渗参数获取

1.1.1试验设计

试验于2021年6月在河海大学节水园区节水与农业生态试验场(31°86′N,118°60′E)开展,供试土壤为粉砂壤土,其砂粒、粉粒、黏粒质量分数分别为17.92%、80.97%、1.11%,容重1.30 g/cm3,电导率2.18 dS/m。土柱试验采用直径10 cm、高100 cm的有机玻璃土柱以及直径15 cm的马氏瓶开展;一维土柱入渗试验共设置8个处理,其初始土壤体积含水率分别为0.11、0.15、0.17、0.19、0.20、0.22、0.23、0.25 m3/m3(T1～T8);各处理入渗水深均为20 mm;入渗时长为70 min;试验过程中实时观测并记录马氏瓶水位变化。

土槽畦灌试验装置长10 m、宽1.5 m、高1.05 m,土槽内土壤深度85 cm、表面坡度0.2%、灌水定额40 mm,入畦单宽流量q为1.0 L/(m·s),改水成数G为9.0,根据曼宁公式计算田面糙率为0.20。土槽试验共设置3个处理(TC1、TC2、TC3),各处理畦首土壤初始体积含水率均为0.17 m3/m3,其初始体积含水率沿程每2.5 m增加0、3%、5%。试验过程中观测累积灌水量、田面水流推进及消退时间以及土槽底部深层渗漏量。

1.1.2入渗参数拟合及累积入渗量计算

采用Koistiakov模型进行一维土壤入渗量计算,其公式为

I=A(θ0)tα(θ0)

(1)

式中I——累积入渗量,m

t——入渗时间,s

α(θ0)——入渗指数

A(θ0)——入渗系数

通过一维土柱入渗试验得到不同初始含水率下的累积入渗量,对入渗系数A(θ0)及入渗指数α(θ0)进行公式拟合,将拟合的公式代入Kostivakov模型,计算土槽试验中土槽沿程各点的累积入渗量,并对比各点累积入渗量与计划灌水量之间的关系。

1.2 畦灌技术要素调控

1.2.1WinSRFR模型应用

WinSRFR[23]是基于零惯性量模型的田面水流运动模拟软件,它可以通过数值分析的方法,模拟地面灌溉过程的进行动态,直观地反映田面水流的推进和消退过程,且能够较准确地评价灌水质量。该软件输入数据有:田块规格(田块的长、宽和田面坡度)、土壤参数(入渗参数和田面糙率)、灌溉管理参数(计划灌水量、单宽流量和灌水时间(改水成数))。输出结果包括:田面水流推进、消退曲线,入渗水深和累积入渗量沿程分布情况,灌水效率以及储水效率等数据。对比土槽试验中实测的田面水流推进时间、消退时间及灌水质量指标与WinSRFR模拟结果,计算决定系数R2和均方根误差(RMSE),对WinSRFR模型进行验证。

1.2.2灌水技术要素优化

选择常见的灌水效率Ea、灌水均匀度Ed和储水效率Es3个指标对土槽试验中不同处理的灌水质量进行评价,其公式分别为

(2)

式中Ws——灌后计划湿润层水量,用水深表示,mm

Wf——灌入田间总水量,mm

Zav——畦田平均入渗深度,mm

Zmin——畦田最小入渗深度,mm

Zr——计划湿润层理论需水量,mm

从式(2)可知,灌水均匀度Ed无法准确反映灌后土壤水分分布的均匀情况,而针对初始含水率不均匀分布的畦灌来说灌后水分的均匀程度尤为重要,因此针对初始含水率沿程不均匀的情况,引入灌后土壤水分均匀度Eu对灌水质量进行评价,其公式为

(3)

其中Zi=Z+θih

式中Zi——观测点总水深,观测点沿畦长方向均匀分布,mm

n——观测点总数,根据畦田长度,每1.0 m取一个观测点

Z——观测点累积入渗量,mm

θi——观测点初始含水率,m3/m3

h——计划湿润层深度,取500 mm

初始含水率沿程不均匀条件下畦田灌水技术要素调控的目标函数为

maxEm=max(aEa+bEu+cEs)

(4)

式中Em——灌水质量综合评价指标,其与Ea、Eu、Es均是关于灌水技术要素组合的函数

a、b、c——权重系数,取值均为1/3

本文选择位于半湿润半干旱地区的河北省沧州市为研究区,根据当地的实际情况,选择入畦单宽流量q、畦田长度L和改水成数G作为灌水技术要素变量,其取值范围分别为:3～9 L/(m·s)、60～100 m、6～8,在各取值范围内将单宽流量平均分为7个水平、畦田长度平均分为9个水平、改水成数平均分为5个水平,一共315种灌水技术要素组合,利用验证好的WinSRFR模型进行模拟,寻求畦田土壤初始含水率沿程增加情况下的最优灌水技术要素组合,最终实现对由降雨径流产生的初始含水率沿程不均匀分布下的畦田灌水技术要素调控。

2 结果与分析

2.1 初始含水率对入渗性能的影响

图2a(图中ob表示观测值;sim表示Koistiakov模型模拟值)中散点表示不同初始含水率状态下土壤累积入渗量的实测值,试验结果显示不同初始含水率条件下累积入渗量随时间的推移而逐渐增加,先表现为非线性特征,而后逐渐转变为线性变化,即土壤入渗由非稳定入渗阶段变为稳定入渗,且随着初始含水率的增加达到稳定入渗的时间逐渐提前,说明初始含水率越高土柱内形成稳定入渗通道所需要的时间越短。当初始含水率大于等于0.25 m3/m3(T8处理)时,入渗很快达到稳定入渗状态,图2a中该处理累积入渗量的曲线可近似为一条直线。在入渗试验的0～20 min之间,T1～T6处理的累积入渗量差异不大;试验开始20 min后各处理表现出明显差异,初始含水率越低,同一时刻的累积入渗量越高。图2a中不同颜色直线表示用Koistiakov模型模拟的不同初始含水率条件下的累积入渗量,T1～T8下Koistiakov模型模拟累积入渗量与实测值R2分别为0.994、0.987、0.982、0.994、0.969、0.945、0.890、0.899,可见Koistiakov模型适用于本试验。

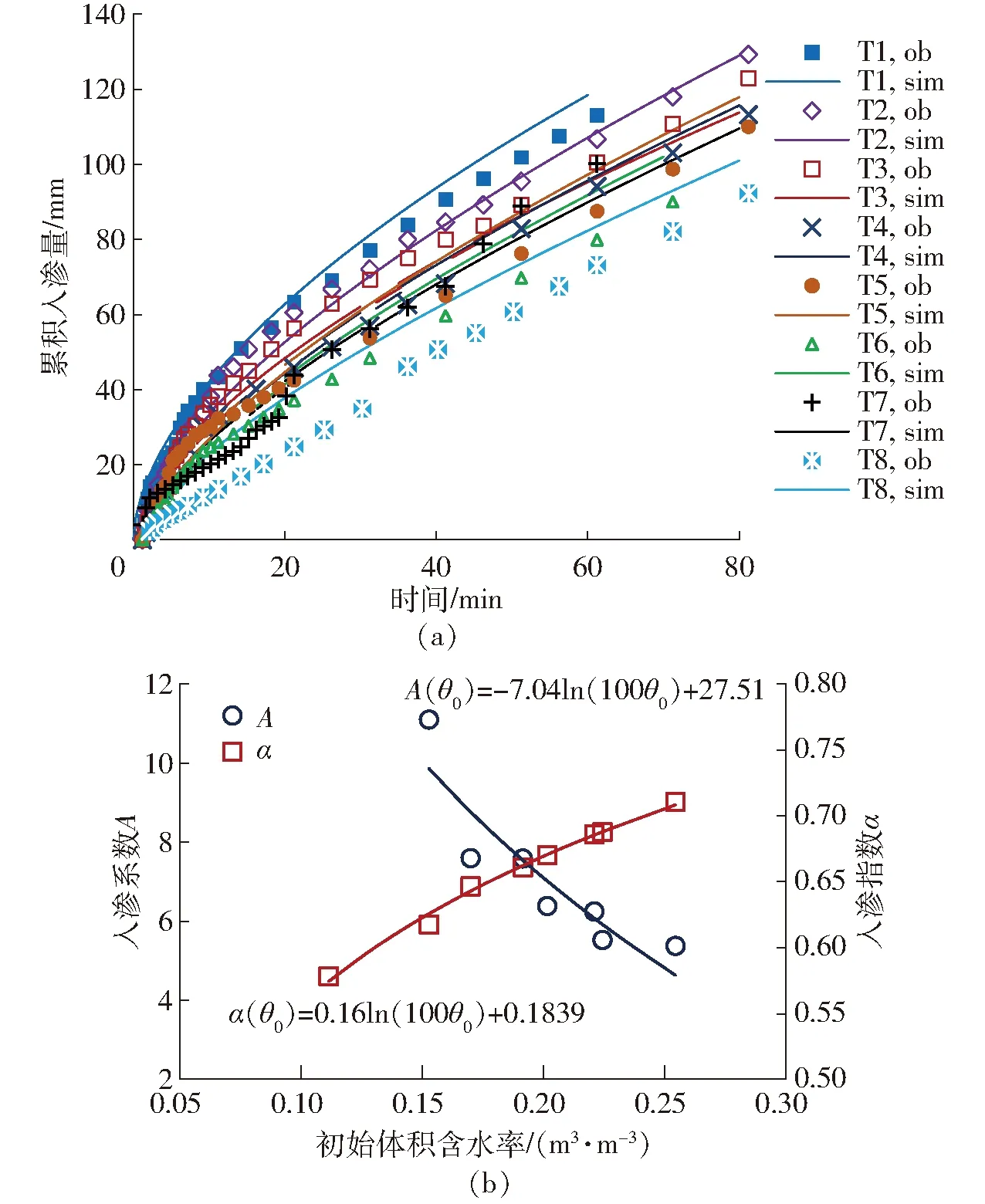
图2 不同土壤初始含水率条件下累积入渗量随时间变化曲线和入渗系数、入渗指数随初始含水率的变化关系Fig.2 Cumulative irrigation,changes of irrigation coefficients and indexes under various initial soil moisture conditions

图2b表示入渗系数A、入渗指数α与土壤初始体积含水率θ0的关系,结果显示当初始体积含水率θ0从11.14%增加到25.45%时,入渗系数A从11.10减小至4.49,减小幅度为59.5%,可见在相同土壤容重、灌水深度以及土壤质地条件下,初始体积含水率θ0对Koistiakov模型入渗系数A的影响较大,入渗系数A随初始体积含水率θ0的增大而下降,且当初始体积含水率θ0增大到一定程度时,入渗系数A减小的趋势会趋于平缓。进一步对入渗系数A与初始体积含水率θ0进行对数拟合,拟合公式为A(θ0)=-7.04ln(100θ0)+27.51,拟合曲线的决定系数R2为0.98,说明入渗系数A与初始体积含水率θ0之间符合对数关系,拟合公式的可信度较高,可用于推测不同初始含水率条件下Koistiakov模型的入渗系数A。入渗指数α与土壤初始体积含水率θ0的变化结果显示,初始体积含水率θ0对入渗指数有较大影响,入渗指数α随初始体积函数率θ0的增大而增大,当初始体积含水率θ0从11.14%增大到25.45%时,入渗指数α从0.578 3增长至0.710 5,增大幅度为22.86%。入渗指数α与初始体积含水率θ0满足对数关系,其拟合公式为α(θ0)=0.16ln(100θ0)+0.183 9,拟合曲线的R2为0.99,可信度较高,表明本公式可用于推测不同初始含水率条件下Koistiakov模型的入渗指数α。

2.2 初始含水率沿程不均匀对畦灌田面水流运动的影响

图3a散点表示土槽试验过程中不同初始含水率分布情况下的田面水流推进与消退情况,结果显示土槽初始含水率分布会影响田面水流推进情况,TC3处理的初始含水率沿程增加幅度最大,其田面水流推进速度也最快,在试验开始后5.41 min推进至土槽末端;TC2处理田面水流推进速度稍慢于TC3处理,在试验开始后6.42 min完成推进过程;而TC1处理土壤初始含水率为均匀分布,其田面水流推进速度最慢,试验开始后7.11 min推进至土槽末端。观察田面水流推进曲线,可以发现3种处理在土槽0～3 m处田面水流推进速度无明显差距,水流推进超过3 m后,田面水流推进速度开始出现差距,其速度由大到小依次为TC3、TC2、TC1,且随着田面水流继续向前推进,田面水流推进的差距逐渐扩大。由此可以看出,随着初始含水率的增加,田面水流推进速度也随之变大,水流推进至末端所需时间减少。当改水成数不变时,土壤初始含水率越高,聚积在土槽末端的水量越大,容易形成深层渗漏,可见当土壤初始含水率沿程增加时,原定灌水方案将会造成畦田灌水质量下降。

图3 不同初始含水率条件下土槽试验水流推进及消退曲线和累积入渗量分布Fig.3 Advances and recessions of border irrigation, and cumulative irrigation along soil box under various initial soil moisture conditions

各处理田面水流消退状况均是土槽首部最先完全消退、末端后消退。田面水流消退速度受土槽土壤初始含水率的影响较大,TC1处理的土槽土壤初始含水率最低,且沿程均匀分布,其田面水流消退速度最快,在17.52 min左右完全消退,土槽首尾消退时间差只有5.77 min;TC2处理的田面水流消退速度相较于TC1出现了明显降低,在27.48 min左右完全消退,土槽首尾消退时间差变大,为12.08 min,超过TC1处理的2倍;TC3处理土壤初始含水率沿程增加幅度最大,该处理田面水流消退速度较TC1处理下降更为剧烈,在46.41 min时才可实现完全消退,且首尾消退时间差进一步拉大,达到27.27 min,约为TC1处理的5倍。

图3b为土槽试验不同处理的累积入渗情况,结果显示各处理累积入渗量沿畦长方向整体上均呈下降趋势,其中TC1处理累积入渗量分布更加均匀,最大、最小值分别为43.57 mm和35.97 mm,差距仅为7.60 mm,但是仅距畦首5.5 m处满足了计划灌水需求;TC2处理下最大、最小累积入渗量分别为51.82、29.48 mm,两者差值为22.34 mm,其中土槽前0～7.5 m部分超过了灌水定额;TC3处理最大累积入渗量高达62.60 mm,累积入渗量最小值仅为18.01 mm,差距高达44.59 mm,该处理也能保证土槽前7.5 m处的灌水量。由此可见,土壤初始含水率沿程增加的条件下,随着土壤初始含水率的升高,田面水流虽然会向土槽末端汇聚,但由于土槽首部初始含水率低,土壤入渗能力更强,田面水位下降速度快,停止灌水后,田面水流会出现倒流现象,首尾初始含水率差值越大,倒流现象越明显,因此累积入渗量差值也越大,换言之当土壤初始含水率沿程增加的幅度越大,其灌水均匀性越差。

2.3 初始含水率沿程不均匀对畦田灌水质量的影响

灌溉后不同处理土槽土壤含水率分布如图4a所示,结合土槽土壤初始含水率分布情况分析可知,灌溉后各处理土槽首部表层土壤含水率最高(体积含水率均超过0.50 m3/m3)。TC1处理土壤初始含水率较低且沿程均匀分布,其入渗深度较为均匀,均在 40 cm 左右;TC2处理距畦首1.0 m处入渗深度达到55 cm,而9～10 m处入渗深度较小,仅为 35 cm;TC3处理整体入渗深度大于前2个处理,平均入渗深度为60 cm,距畦首2.0 m处入渗深度超过70 cm,可形成深层渗漏。

图4 不同处理灌后土槽土壤水分分布和灌水质量评价指标Fig.4 Distributions of soil moisture and evaluation indexes of irrigation quality under different experiment treatments

不同处理灌水质量评价结果显示(图4b),在灌水技术要素保持不变的条件下,各处理储水效率均保持在一个较高的水平,分别为98.57%、97.12%和100%;TC1处理灌水效率和灌水均匀度最高,分别为100%和92.50%,TC3处理最低,灌水效率和灌水均匀度分别为91.56%和45.50%,说明TC1处理对灌入水分的利用效率最高,灌溉水量沿畦长方向上分布更加均匀。综合灌水质量指标Em结果显示,TC1处理灌水质量综合评价指标最高(97.86%),TC3处理最低(91.85%)。由此可见,土壤初始含水率沿程增加时,按初始含水率均匀分布状态下的灌水技术要素组合进行灌溉会导致灌水质量下降,且土壤初始含水率沿程增幅越大,灌水质量下降越明显。

2.4 土壤初始含水率沿程不均匀条件下畦灌技术要素优化

2.4.1WinSRFR模型验证

基于土槽试验土壤初始含水率分布情况,结合土柱试验得到的入渗系数、入渗指数与土壤初始含水率关系式,得到WinSRFR模型所需的模拟参数(表1)。利用WinSRFR模型模拟土槽灌溉试验中的田面水流运动,模拟结果如图3a实线所示,结果显示,各处理土槽中后段田面水流推进速度实测值小于模拟值,这是由于试验过程中田面实际水深大于试验设计值,导致实际土壤入渗能力大于理论计算值,使得田面水流推进实际速度小于模拟值。而同样在土槽中后段,实测水流消退速度较模拟结果更快,这是因为WinSRFR数学模型假定只存在垂向入渗,实际试验中存在的水平入渗使得消退速度变快。TC1处理实测和模拟水流推进、消退曲线均属于强相关性,R2均大于0.99,两者推进时间的RMSE仅有0.41 min,占整体推进时间的5.77%,消退曲线RMSE为0.56 min,占总时间的3.16%;TC2处理实测和模拟水流推进、消退曲线也属于强相关性,R2均大于0.99,其水流推进模拟与实测RMSE为0.46 min,占整体推进时间的7.29%,TC2处理田面水流消退模拟与实测RMSE为0.82 min,占总时间的2.98%;TC3处理实测和模拟水流推进、消退曲线相关性良好,R2均大于0.99,其水流推进模拟与实测RMSE为0.38 min,占整体推进时间的7.13%,TC3处理田面水流消退模拟与实测RMSE为1.55 min,占总时间的3.36%。

表1 WinSRFR模拟所需入渗参数Tab.1 List of parameters for irrigation in WinSRFR model

由图4b可知,Ea、Eu和Es的模拟值均高于实测值,其误差均在5%以内,均方根误差分别为1.49%、1.65%和0.97%。综合田面水流运动及灌水质量评价指标模拟与实测对比结果可见,将本研究得到的土壤初始含水率与入渗指数、入渗系数关系式代入WinSRFR模型来模拟畦灌田面水流运动以及评价畦灌灌水质量的准确性良好,结果可靠,可用于进行初始含水率沿程不均匀的畦灌水流运动模拟及灌水技术要素优化。

2.4.2降雨后畦田参数分布

参考文献[24-28],假定畦田降雨产流后土壤含水率沿程均匀增加,并且设定畦首土壤含水率为0.189 0 m3/m3,畦尾土壤含水率为0.464 3 m3/m3,则畦田土壤初始含水率分布函数为

(5)

式中θ0(x)——与畦首距离x处土壤初始体积含水率,m3/m3

x——与畦首距离,m

将降雨后畦田土壤初始体积含水率分布函数(式(5))代入土柱试验得到入渗系数和入渗指数与土壤初始含水率的对数关系式,得到降雨产流后畦田入渗参数分布情况,即

(6)

式中A(x)——与畦首距离x处土壤入渗系数

α(x)——与畦首距离x处土壤入渗指数

2.4.3畦灌技术要素优化

图5表示不同灌水技术要素组合下,降雨产流导致的畦田初始含水率不均匀情况下的灌水质量模拟结果。如图5所示,在畦田土壤初始含水率沿程增加的条件下,当改水成数G在6.0～6.5、单宽流量q在5～9 L/(m·s)、畦田长度L在 80～100 m之间时,灌水质量综合评价指标均高于80.0%;当改水成数G在7～8、单宽流量q在 4～5 L/(m·s)、畦田长度L在75～100 m之间时,畦田灌水质量综合评价指标均在75.0%以上;相同畦田长度L和入畦单宽流量q条件下,畦田灌水质量随着改水成数G的增大而逐渐减小,相同改水成数G和单宽流量q条件下,畦田灌水质量随着畦田长度L的增加而增加。当土壤初始体积含水率沿程由0.189 0 m3/m3均匀增加至0.464 3 m3/m3时,为保证畦田灌水质量、提高水分利用率,改水成数G宜取6.0～6.5、单宽流量q应控制在5～9 L/(m·s)之间,畦田长度L宜设定为80～100 m之间。当畦田长度L为85 m、单宽流量q为7 L/(m·s)、改水成数G为6时,土壤初始含水率沿程增加的畦田灌水质量最高,其灌水效率Ea为75.0%,土壤水分均匀度Eu为78.3%,储水效率Es为100%,其灌水质量综合评价指标为84.5%。

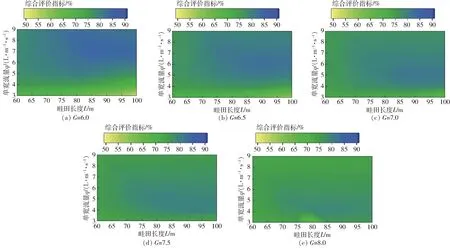
图5 不同灌水技术要素组合下灌水质量分布图Fig.5 Irrigation quality distribution under different combinations of irrigation technical factors

3 讨论

土壤累积入渗量可反映土壤入渗能力,本研究发现入渗初期累积入渗量随初始含水率的增大而减小,这与张强伟等[29]的试验结果一致,可见土壤初始含水率是影响水分入渗能力的关键因素[30]。在土壤水分入渗初期,本研究各组初始体积含水率差异较大,随着入渗过程的推进各组含水率差异逐渐缩小,累积入渗量之间的差异也随之减小。当土壤初始含水率较低且处于非饱和状态时,水分入渗主要靠土壤基质势以及毛管力驱动,即因灌溉来水,上层土壤含水率快速升高,与下层土壤间形成较大水势梯度,进而促进水分入渗[31]。当土壤初始含水率较高时,土壤团聚体遇水易出现膨胀崩解现象使得土壤孔隙度降低,形成不透水结皮,从而降低土壤入渗速率[32]。

Koistivakov模型的入渗系数与土壤水势、结构和质地有关[33]。在土壤结构和质地相同的条件下,土壤水势是影响入渗系数的唯一因素,而土壤水势与土壤含水率之间存在函数关系[34]。土壤水分入渗中后期,表层土壤迅速饱和,水分运动可近似看成饱和土壤水分运动[35];当过水面积不变时,土壤入渗通量由水势梯度决定,而在此条件下水势梯度由土壤含水率决定,初始含水率越低水势梯度越高,入渗系数越大。入渗指数反映入渗过程中土壤入渗能力的衰减情况,其值与土壤水势以及土壤质地有关[36-37]。在土壤质地相同的条件下,入渗指数只受土壤水势的影响。水分入渗过程中,土壤初始含水率越高,过水断面上下的含水率差值越小,水势梯度越小,入渗过程越难,土壤入渗能力衰减得更加明显,入渗指数会有所增大[38]。

畦灌水流运动可分为沿畦长方向推进以及向下入渗两部分,水流运动受畦田坡度、田面糙率以及畦田初始含水率等因素影响[39-41]。土壤初始含水率是影响土壤入渗性能的关键因素,入渗速率影响畦灌水流消退过程[42]。本研究中土槽试验结果显示,在土槽相同位置上田面水流消退时间由小到大依次为TC1、TC2、TC3(图3a),且各处理间消退时间差随着位置逐渐向土槽末端靠近而逐渐变大。这是由于初始含水率越高土壤入渗能力越低,当灌水定额和改水成数一定时,畦田土壤初始含水率沿程增加,会导致畦灌水流入渗逐渐受阻,田面水流消退沿程逐渐变慢。本试验还发现,初始含水率较高时,畦灌水流推进速度较快,这是由于高含水率条件下土壤颗粒蓄水能力较弱,土壤水力传导度提高,减少了水流在水平方向上的运移阻力[43],加之初始含水率较高处水流消退速度较慢,会导致此处土壤表面受水时间过长,即入渗过程偏长,但由于初始含水率升高会降低土壤的入渗能力,故初始含水率对畦田灌水质量的影响还有待进一步研究。畦田初始含水率影响畦田水流运动,进一步会影响灌后土壤水分分布情况;灌水效率、灌水均匀度、储水效率等畦灌评价指标均与灌后土壤含水率有关[44]。在畦灌技术要素相同的情况下,畦田含水率沿程越不均匀,灌水质量越低(图4b),说明在初始含水率不均匀的条件下,若依然按照畦田初始含水率均匀条件制定的畦灌技术要素进行灌溉会降低灌水质量。

本研究发现,在畦田初始含水率沿程增加的条件下,当畦田长度大于80 m时灌水质量较优,这与聂卫波等[45]的结论一致;这是由于畦田过短,畦田末端易出现壅水现象,进而增大田间渗漏,同时畦田初始含水率沿程增加又会加重这一现象,进一步降低灌水质量。有研究[46]认为,畦田长度30 m内单宽流量对灌水质量无显著影响,而本研究结果显示,在改水成数为6的情况下,高单宽流量可以取得较高灌水质量,这可能是因为选择较大的单宽流量可以克服田面糙率对灌水质量造成的不利影响,加强水流对地面的冲刷作用,促进土壤颗粒运移从而提高田面平整度,进而改善灌水质量[47],但实际灌溉中盲目加大入畦流量不仅会增加渗漏风险还易破坏作物,因此,仍需依据实际情况制定畦灌技术要素。本研究认为畦田灌水质量随着改水成数G的增大而逐渐减小,该结论与王洋等[48]的试验结果存在差异,这是由于在土壤含水率沿程增加的条件下,过晚的改水易使畦田末端产生壅水,发生深层渗漏,降低灌水效率以及灌水均匀度,进而影响灌水质量评价[49]。综上,本研究认为在畦田土壤初始含水率沿程增加的模拟条件下,畦田长度L为85 m、单宽流量q为 7.0 L/(m·s)、改水成数G为6时可获得最优灌水质量。

4 结束语

本文结合一维土柱入渗试验及二维土槽灌溉试验数据,利用WinSRFR模型模拟降雨产流后畦灌过程,获取灌水质量评价指标,从而对畦灌技术要素进行调控优化。结果表明,在相同土壤容重、灌水深度以及土壤质地条件下,入渗系数随土壤初始含水率的增大而减小,入渗指数随土壤初始含水率的增大而增大;土壤初始含水率沿程增加的条件下,畦田田面水流推进速度加快,消退速度减缓,畦田首尾入渗不均匀,若以正常灌水技术要素组合进行灌溉会引起灌水质量下降;通过灌溉技术要素优化可得,当畦田长度L为85 m、单宽流量q为7.0 L/(m·s)、改水成数G为6时,土壤初始含水率沿程增加的畦田灌水质量最高,其灌水效率Ea为75.0%,土壤水分均匀度Eu为78.3%,储水效率Es为100%,综合灌水质量为84.5%。