农用多旋翼无人机作业能耗白盒模型构建与试验

2023-08-22李继宇张植勋赵胤伟刘知杰

农业机械学报 2023年8期

李继宇张植勋赵胤伟沈卓刘知杰吕佳

(华南农业大学工程学院, 广州 510642)

0 引言

当前我国农用无人机在所有机型中超过80%,农用无人机的优势主要体现在:用途广泛,无人机在农业领域可以进行喷药施肥[1]、授粉播种[2]、农情监测[3]、生物检测[4]和放牧喂食[5]等任务。使用方便效率高,其作业地形不受限制,还可以通过航线完成监测和撒药等作业,植保用药效率高,可以最大程度减少病虫害;经济效益明显,例如其单位植保费用相比传统方法低30%～50%,效率是人工的20～50倍。

农用无人机根据类型可以分为单旋翼、多旋翼、固定翼,按旋翼类型目前主要有4旋翼、6旋翼、8旋翼及更多旋翼构型,目前大规模使用的是4旋翼和6旋翼。根据能源类型可以分为电动和油动,其中无人机电动转换效率为70%,油动转换效率为30%,因此本文针对以锂电池为动力的农用无人机进行研究。目前商品锂电池的能量密度普遍低于200 W·h/kg,使得农用无人机配套的电池可供续航时间最多为20 min,难以满足当前农用无人机对长航程、长航时、大负载的作业需求。虽然增加电池数量和减少载荷可以提高续航能力,但前者增加重量,导致额外的能量消耗,后者降低了效率[6]。为了降低因电池容量有限而导致无人机飞行时间有限的影响,对农用无人机在飞行时的作业能耗进行研究是十分必要的。

目前针对农用无人机作业能耗研究主要围绕黑盒或白盒建模。黑盒建模主要通过数据预处理、回归法、实验法和测试法等针对整体系统的各个模块实际的作业能耗数据进行采集,并拟合成有关函数进行建模。ABEYWICKRAMA等[7]通过使用实验法对无人机各种状态下电池使用情况进行研究,得到一个完整的无人机能耗模型,但该方法只针对单款无人机在单种电池使用情况下进行研究,缺乏对无人机系统的原理性分析。PRASETIA等[8]通过使用数据收集、数据预处理和回归法提出了一种基于任务的无人机能耗预测模型,然而该方法缺乏对无人机能耗规律的研究。林晋立等[9]通过测试法搭建测试平台构建了针对多旋翼农用无人机功率能耗计算的理论模型,不过该方法并未通过实际飞行测试,只使用试验架进行固定测试。ÇABUK等[10]通过黑盒模型中经验测量法得出每个子系统能耗对整体能耗的影响,但该研究缺少对电机这个消耗最大的子系统进行进一步原理性分析。TRAUB[11]通过测试法使用不同种类锂电池进行风洞研究以评估电池放电行为,得到一个准确的续航估计值,通过研究电池在无人机飞行过程的能耗消耗情况对农用无人机作业能耗的研究具有一定的借鉴意义。黑盒建模研究虽然可以更加准确得到无人机的模型,但只是针对被测无人机进行建模,且需要大量重复的试验,存在一定局限性。

白盒建模主要通过研究整体性系统的各个模块(包含电机、螺旋桨、电池、电调等)或者飞行任务下的原理推导进行建模。DORLING等[12]通过整体建模方法推导得出多旋翼无人机在悬停时的能耗,主要重点是将消耗的功率与无人机重量联系起来,没有分析在飞行、起飞或着陆期间的能耗。ACHTELIK等[13]通过研究微型飞行器上4个以上螺旋桨和电机的影响,针对几种类型的多旋翼进行建模,以比较它们的动力学、效率和冗余,然而该方法只针对螺旋桨和电机进行建模分析,缺乏对整个动力系统进行建模和分析。SHI等[14]通过研究螺旋桨、电机、电调、电池这4个动力系统的主要部件,得到适合多种机型性能综合评价方法,不过该方法仅针对无人机进行静态模型建模,没有对有关动态模型建模的进一步分析。BEZZO等[15]研究飞行任务3个阶段的能耗特点,然而该研究最后只专注于匀速段路径,忽略了路径的加速部分和减速部分。白盒建模研究相较于黑盒建模减少了比较多的重复性试验,从原理性分析可以更好地了解农用无人机任务飞行的能耗变化特点,且通过该方法建立的模型可以更好的规划无人机任务以降低能耗。

国内外学者已从不同的角度对无人机作业能耗建模进行研究,提供了较高的参考价值。对于目前针对农用无人机飞行任务下不同飞行参数下的作业能耗缺乏有效评估的问题,本文在前人研究的基础上,通过白盒建模方法针对农用无人机动力系统各个能耗部件进行建模,并结合农用无人机任务中的飞行过程得到作业能耗模型,通过建立一个可靠且完整的农用无人机作业能耗模型,来评估飞行任务下的作业能耗。同时上述国内外研究所使用的无人机大多数轴距和尺寸较小,比较适用于航拍、巡检等简单任务,没有针对农用无人机的任务特点进行研究。因此,本研究针对农用无人机飞行任务中的速度、航程和载荷这3个动态参数设计试验,并进行试验验证,以验证模型的有效性。

1 白盒理论模型构建

理论模型主要是由电池输入功率和螺旋桨输出功率的总效率模型以及克服重力所做的功、加速减速段所做的功和克服空气阻力所做的功的做功模型组成,其中总效率模型表示电池输入功率到螺旋桨输出功率的转化关系。如图1所示,首先根据农用无人机所使用的动力系统的螺旋桨、电机、电调和电池这4个组件的原理进行白盒建模[16],得到总效率模型,然后根据所得到的无人机总效率模型结合无人机飞行过程的动态飞行参数,计算出无人机匀速直线飞行所需的能量,包括保持无人机高度所需能量与克服空气阻力所需能量的总和,最终得到农用无人机的作业能耗模型。

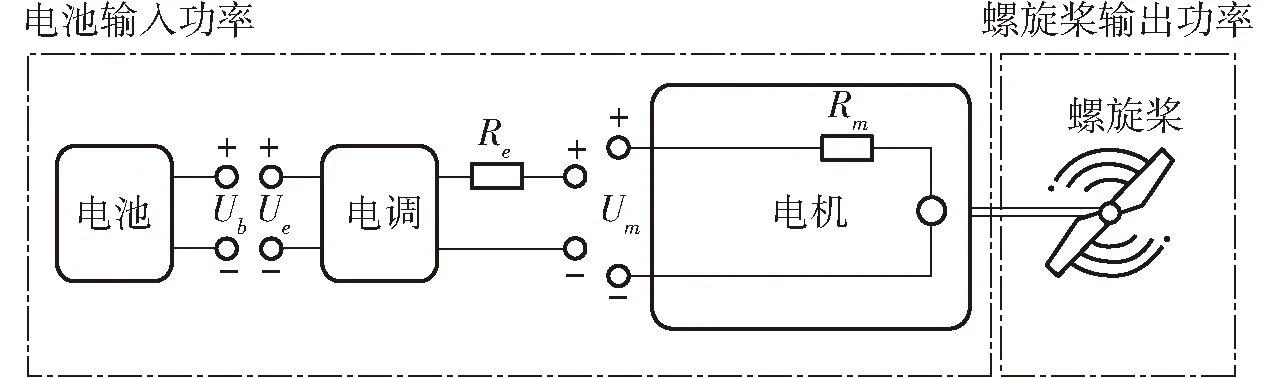
图1 总效率模型示意图Fig.1 Schematic of total efficiency model

当前作业能耗模型的输入参数为动力系统参数和飞行参数。其中动力系统参数是来自所使用无人机供应商提供的参数,飞行参数是来自飞行任务时所设定的参数,阻力参数中无人机受空气阻力影响的有效面积近似为无人机最大截面面积[17],阻力系数为无人机整体的阻力系数[18]。

1.1 总效率模型构建

为了得到总效率模型,需要对农用无人机所使用的动力系统螺旋桨、电机、电调和电池这4个组件进行建模。在建模时首先需要计算螺旋桨输出功率,再根据螺旋桨输出功率对应的螺旋桨转速和转矩,求出电池输入功率。

1.1.1螺旋桨输出功率

农用无人机在不同任务下有不同的高度,处于不同环境也存在不同的温度,不同高度和温度下的大气压强和空气密度不同,这两个因素都直接影响无人机螺旋桨所提供的推力,进而对无人机的能耗存在影响。将无人机当前高度h和温度Tt输入,求解出当前大气压强pa[19]和空气密度ρ为

(1)

(2)

式中ρ0——标准空气密度

农用无人机通常采用定直径和定螺距的螺旋桨,螺旋桨转速N[20]为

(3)

(4)

(5)

式中T——单个螺旋桨所提供的拉力

DP——螺旋桨直径

CT——螺旋桨拉力系数

m0——整机质量

g——重力加速度

np——螺旋桨个数

λ——叶片翼型面积修正系数

ξ——位置系数

BP——桨叶数量

K0——升力曲线斜率

ε——下洗气流校正因子

βp——螺旋桨桨叶角

α0——螺旋桨零升力角

A——展弦比

螺旋桨转矩是指螺旋桨运转时克服空气阻力所需的转矩,则螺旋桨转矩M[21]为

(6)

其中

(7)

(8)

式中CQ——螺旋桨转矩系数,是螺旋桨转矩的无纲量系数

Cd——螺旋桨叶片截面翼型的阻力系数

Cfd——零升阻力系数

e——奥斯瓦尔德效率因子

螺旋桨桨叶角定义为中螺旋桨的旋转平面(A-B)与螺旋桨桨叶弦线(A-C)之间的夹角。假设其沿其半径方向保持不变,则桨叶角βp为

(9)

式中HP——螺旋桨螺距

将上面建模得到的螺旋桨拉力特性和转矩特性与常见二叶螺旋桨试验数据进行比较,综合考虑不同螺旋桨的型号和工艺,选取一组适应性较广的平均参数[22],则取值为:A=5,ε=0.85,λ=0.75,ξ=0.5,e=0.83,Cfd=0.015,α0=0°,K0=6.11。

综合以上公式可计算螺旋桨输出功率Pp为

(10)

1.1.2电池输入功率

在飞行中,螺旋桨和电机可以视为一个整体,所以螺旋桨转矩等价于电机负载转矩、螺旋桨转速等价于电机空载转速,而且农用无人机一般使用无刷直流电机,无刷电机可以等效为一个永磁直流电机模型[23],结合电机基本参数可得出电机等效电压Um和电机等效电流Im[24]为

(11)

(12)

式中KT——电机转矩常数

KE——电机反电势常数

Im0——电机空载电流

Rm——电机内阻

电机转矩常数KT和电机反电势常数KE存在关系式[24],为

KT=9.55KE

(13)

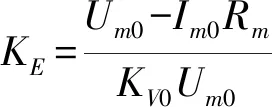
(14)

式中Um0——电机空载电压

KV0——电机空载KV值

电调调制下无刷电机的转速范围主要取决于电机负载转矩与电池电压,所以电调调节占空比后的等效直流电压Ue为

Ue=Um+ImRe

(15)

式中Re——电调内阻

电调输出电压占空比可以等效反映油门大小,所以电调输出电压占空比σ和电调输入电流Ie为

(16)

Ie=σIm

(17)

式中Ub——电池电压

电池除了提供动力系统的电流,还提供其他机载设备(如飞行控制器、机载计算机等)电流,同时电池电流在传输过程会出现电流损耗,根据测算这部分所消耗的电流Io一般约为1 A。所以电池电流Ib为

Ib=nrIe+Io

(18)

综合以上公式得电池输入功率Pb为

Pb=UbIb

(19)

1.1.3总效率模型

最终根据螺旋桨输出功率Pp和电池输入功率Pb得到总效率ηtotal为

(20)

1.2 作业能耗模型构建

为了构建最终的作业能耗模型,对农用无人机的整个飞行过程的作业能耗参数进行研究。其中作业能耗参数中无人机的载荷主要影响飞行时克服重力所做的功,速度和无人机航程主要影响整段飞行任务的作业能耗。建模时结合总效率模型后,再对飞行任务中速度、航程和载荷的这3个动态参数进行分析,得到最终的作业能耗模型。如图2所示,无人机飞行时克服重力所做的功为EG,在带载荷时还会受到额外的重力影响。再根据动能定理,得到加速减速段所做的功为EK,最后结合阻力所做的功为ED,经过总效率模型转换得到所需作业能耗E。

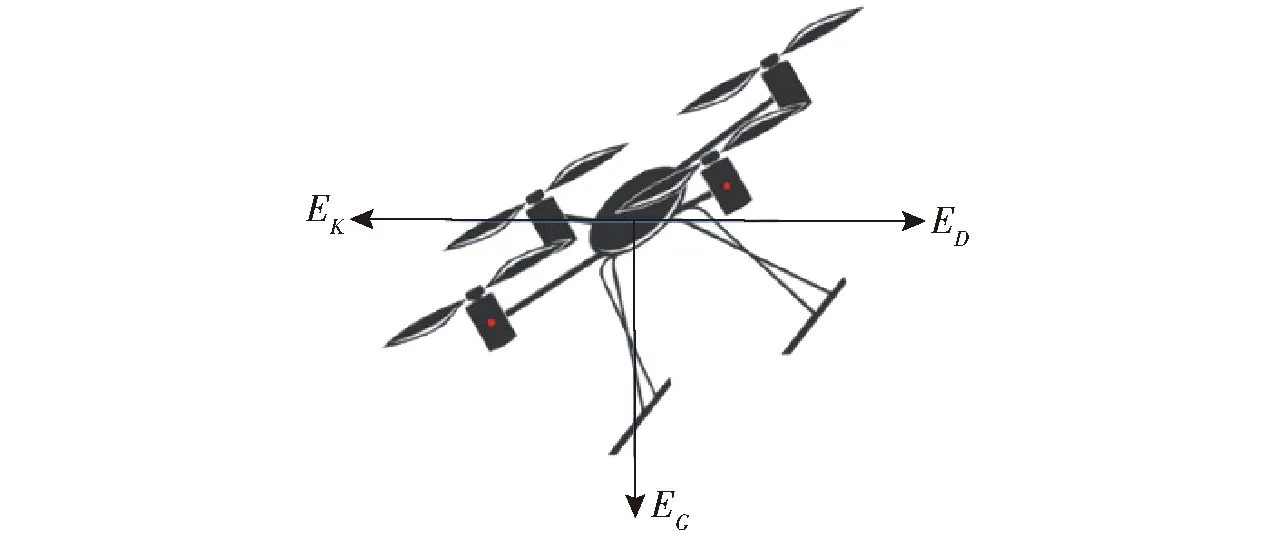
图2 作业能耗示意图Fig.2 Schematic of dynamic energy consumption

1.2.1无人机克服重力所做的功EG

根据激励盘理论,螺旋桨可以简化为一个无厚度可穿透的圆盘[25],所有螺旋桨圆盘的总面积At为

(21)

在飞行时,空气流过螺旋桨,向下推动空气,螺旋桨每秒向下推动的空气质量mα为

ma=ρAtva

(22)

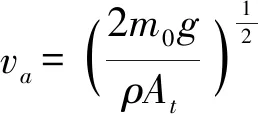
(23)

式中va——流过螺旋桨圆盘的空气速度

所有螺旋桨对空气质量ma施加的力FP等于无人机的重力,FP为

FP=mava=m0g

(24)

最后可得功率P0[26]为

(25)

农用无人机沿着直线飞行,如图3所示。在t0时刻,从v0开始加速直到在t1达到速度v1。保持速度直到t2,在t3减速到v0,假设速度v1和v2相同,速度都等于v,无人机克服重力所做的功EG为

图3 加速减速段所做功示意图Fig.3 Schematic of work done by acceleration and deceleration sections

(26)

式中d——飞行距离v——飞行速度

a——加速度

1.2.2加速减速段所做的功EK

根据动能定理,如图3所示,假设速度v1和v2相同,且等于设定速度v,则加速减速段所做的功相同,EK为

EK=m0v2

(27)

1.2.3克服空气阻力所作的功ED

在飞行过程中,无人机受到空气阻力影响,无人机所受阻力FD[27]为

(28)

式中Ae——无人机受空气阻力影响的有效面积

CD——阻力系数

农用无人机沿着直线飞行,会持续受到空气阻力,则克服空气阻力所做的功ED为

(29)

1.2.4农用无人机作业能耗

根据叠加原理,综合克服重力所作的功为EG、加速减速段所做的功为EK、阻力所做的功为ED,再经过总效率模型转换得到所需要提供的动态能量,得到最终的作业能耗模型E为

(30)

2 模型验证

设计不同的试验来验证所构建作业能耗模型的有效性。对于农用无人机飞行任务下的应用场景,农用无人机应用在不同任务下需要携带不同的设备即挂载质量不同的载荷[28],如测绘需要挂载相机,遥感需要挂载高光谱成像仪,施药需要挂载药箱等,对于不同任务下需要设定不同的速度,不同地块也需要设计不同长度的航程。因此针对农用无人机飞行任务中速度、航程和载荷的这3个动态参数,设计试验对比不同速度、航程和载荷下机载采集设备采集得到的作业能耗数据与相同条件下理论模型计算的作业能耗数据,以此来验证模型的有效性。

2.1 试验场地

试验在华南农业大学华山运动场和华南农业大学教学科研基地进行。试验期间使用Kestrel的NK5500型气象站记录风速和风向,如图4所示。试验时风速基本集中在3.3 m/s以下,根据风力等级划分,风速3.3 m/s以下为轻风,气象环境较为稳定,符合试验要求[29]。

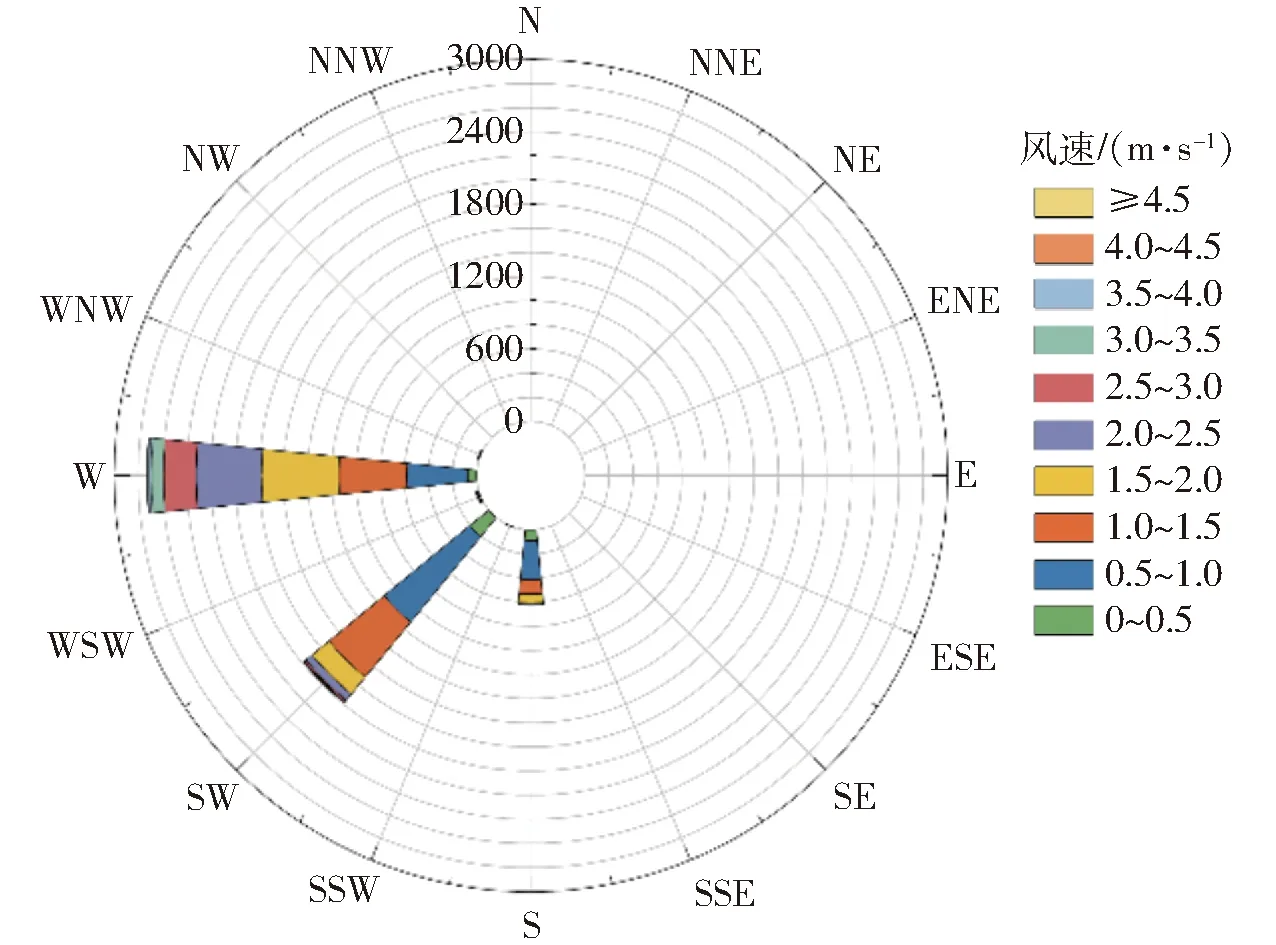
图4 风速及风向Fig.4 Wind speed and direction

2.2 材料和设备

为了验证所得到的作业能耗模型,所有试验主要使用自行组装的专用型无人机A(型号为飞越X6,华南农业大学无人机创新实验室),最大挂载载荷为2.5 kg,可挂载摄像机、高光谱相机或播种装置等农用设备。目前该机型设计最大前飞速度为12 m/s,单程最长飞行距离为6 km。可满足试验的需求。本次试验还使用了通用型无人机B(型号为大疆S1000,大疆创新科技),为2014年发布的通用消费级航拍无人机,而该无人机为当年的通用级载机,因其稳定安全的飞行性能,广泛应用于各种无人机应用领域,如图5所示。两架无人机的动力系统详细的配置参数是厂商提供动力系统各个部件的理论参数,如表1所示。

表1 试验农用无人机基本参数Tab.1 Basic parameters of experimental agricultural UAV

图5 试验无人机Fig.5 Tested UAV

其中机载采集设备采用机载计算机(型号为NVIDIA Jetson TX2,英伟达),用来运行机器人操作系统(ROS),使用该系统外部获取功率计采集的电池电压和电流信息以及RTK定位系统的定位数据。其中功率计是一款库仑计(型号为95V/200A,战锂智能科技),可以检测电池输出的电流、电压和负载功率。电压测量范围为0～95 V,数据采样频率5 Hz。功率计所配的分流器为200 A/75 mV。其中RTK定位系统采用全系全频点高精度GNSS板卡(型号为K705,司南导航),支持北斗全球信号的接收,配合地面基站支持RTK定位。

2.3 试验方法

针对农用无人机飞行任务中速度、航程和载荷这3个动态参数来设计试验。在动态参数选择上,结合当前农用无人机的作业特点及调查了解,对于速度动态参数选择上,目前如大疆和极飞等农用无人机在携带载荷的情况下速度最快在10 m/s左右,本试验所用专用型无人机A最大前飞速度为12 m/s,所以在设计试验时将最快速度设定为12 m/s,从4 m/s开始,以2 m/s为梯度进行递增。对于载荷动态参数选择上,农用无人机在飞行时的能耗与产生的推力成正比[13],在一定范围内,农用无人机所携带的载荷越大,能耗越高,同时考虑到飞行时的安全因素和易实现性,所以在设计试验时选用0～1.5 kg进行试验,以0.5 kg为梯度进行递增。对于航程动态参数选择上,无人机在飞行任务时主要是对每段航程进行规划,所有的航程组成飞行任务,所以在设计试验时选用150 m和300 m进行试验。

如图6所示,针对速度参数,在保证航程和载荷不变的情况下,使用无人机A和B分别进行速度组的8组试验;针对航程参数,在保证载荷不变的情况下,设计使用无人机A进行航程组的10组试验;针对载荷参数,在保证航程不变的情况下,设计使用无人机A进行载荷组的12组试验,得到对应参数的作业能耗数据。试验无人机的飞行参数如表1所示。在飞行前在地面站设置好参数,其中所有试验组的加速度均设置为1 m/s2,在飞行试验时的无人机会根据目标设定的加速度加速和减速飞行,根据对应的速度进行设置,飞行的航线根据对应航程进行设置,并上传到飞行控制器中,开始飞行任务。

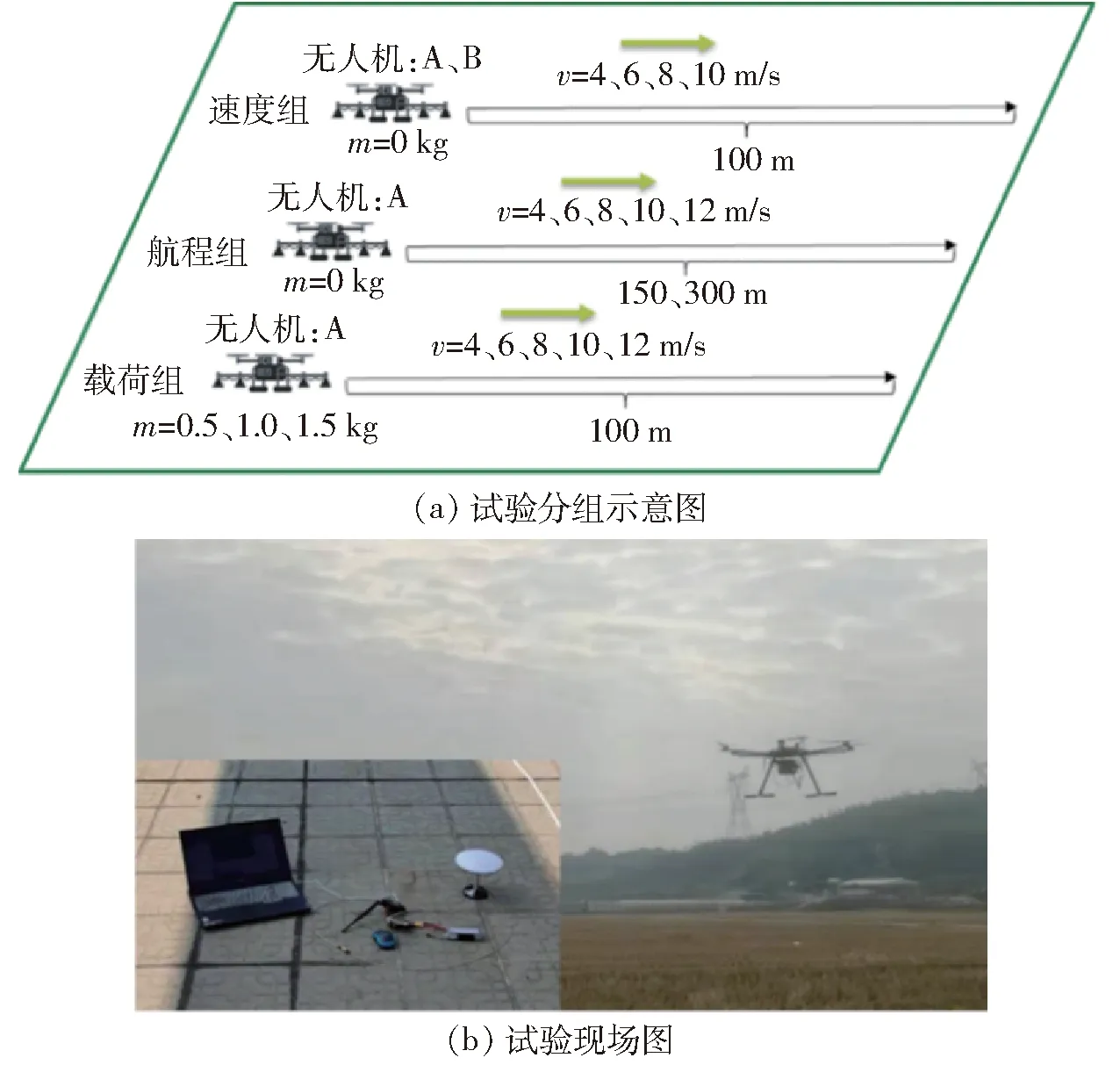
图6 试验方法Fig.6 Test method

3 试验结果对比分析

为了验证模型的有效性,在试验后将速度、航程和载荷组分别由机载采集设备采集得到的试验作业能耗数据进行处理后,结合表1试验农用无人机的基本参数,在相同条件下与使用工程计算软件Maple计算理论模型得到的作业能耗进行对比,得到两者的误差。进一步对模型的各个参数进行分析,引入模型修正系数对模型的输入参数进行修正,得到实际试验的速度和加速度数据,再代入模型计算出修正后的理论模型作业能耗,并与修正前进行对比,得到修正后的结果。

3.1 理论计算作业能耗与试验作业能耗对比

首先通过模型计算速度、航程和载荷组的作业能耗,根据表1使用工程计算软件Maple计算理论模型对应的作业能耗。为了求出速度、航程和载荷组的作业能耗,需要对机载采集设备采集的数据进行处理。机载采集设备运行的ROS系统在试验时会采集北斗RTK和对应能耗数据,并将其自动处理及保存,根据ROS系统采集得到的数据计算得出每个组的作业能耗,如表2所示。

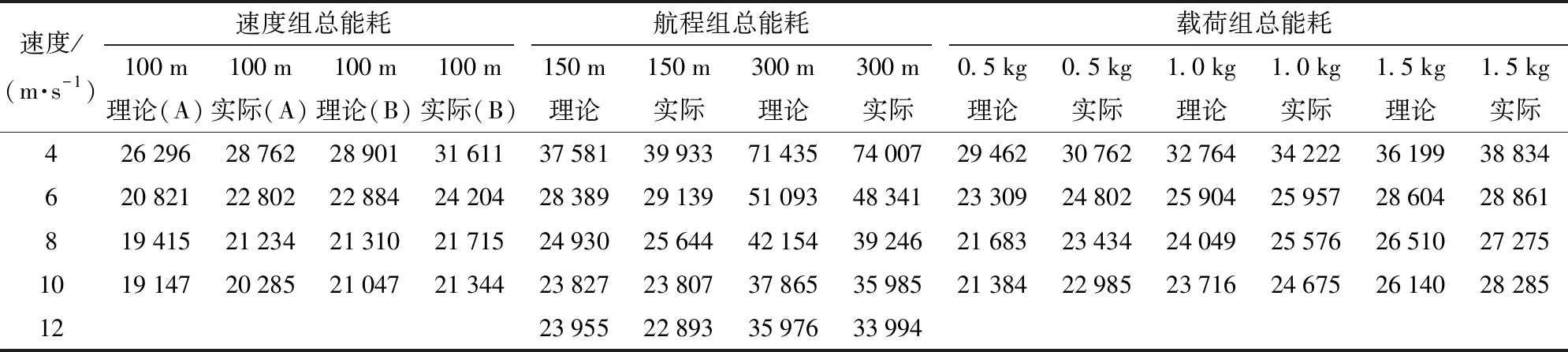
表2 不同设定速度组在不同航程下的理论计算和试验作业能耗Tab.2 Theoretical calculation and experimental dynamic energy consumption of different set speed groups under different voyages J

将理论计算的作业能耗和对应的试验作业能耗数据进行汇总,如图7所示,可以看出理论计算的作业能耗和实际试验得到的作业能耗的变化情况。

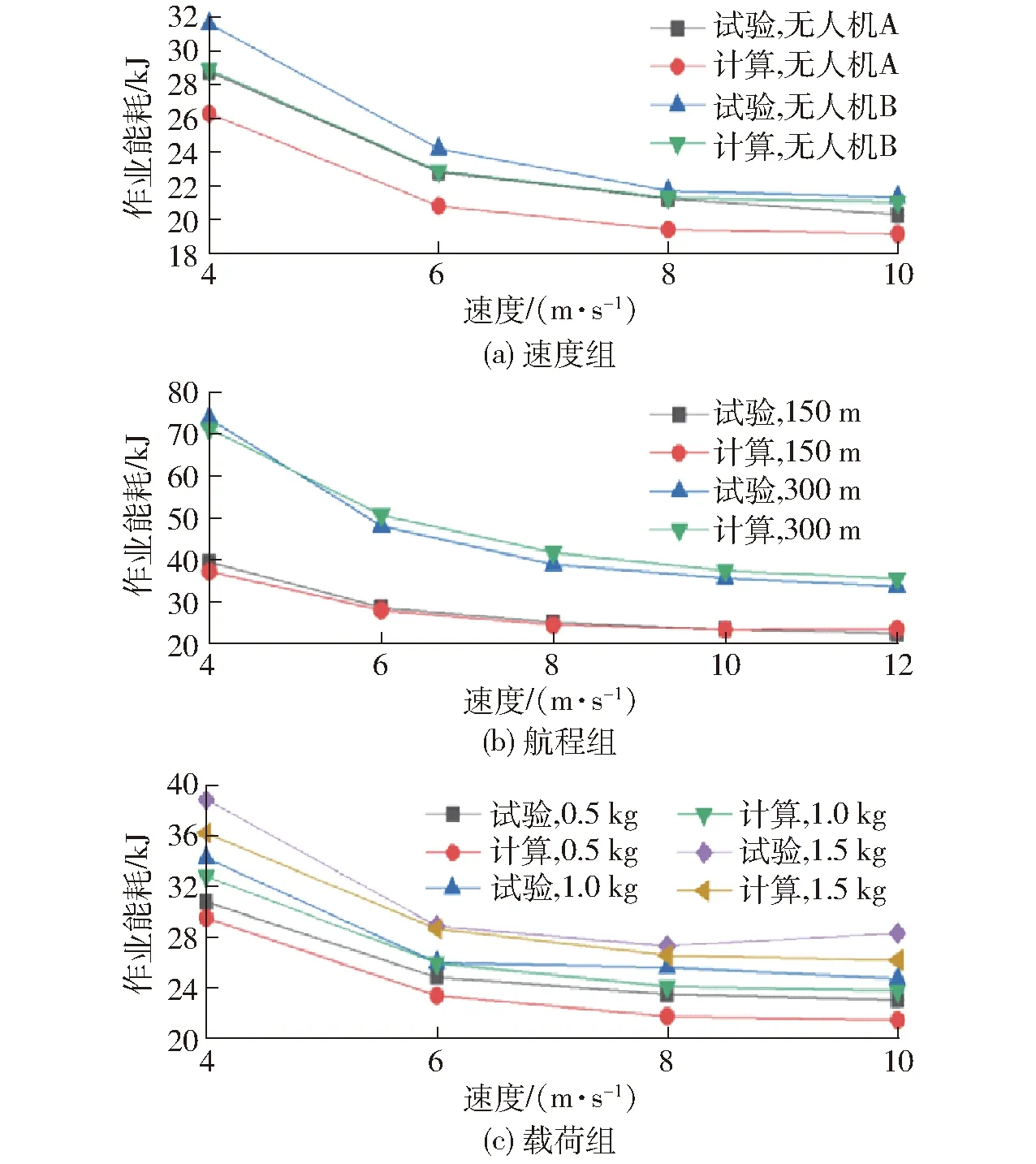
图7 不同速度、航程、载荷时理论计算和试验作业能耗变化曲线Fig.7 Theoretical calculations and experimental operational energy consumption for three groups

将3组的理论计算和试验作业能耗进行对比,代入误差计算公式

(31)

式中x——理论计算的作业能耗

r——实际试验得到的作业能耗

可以得到理论模型计算的作业能耗数据与实际试验得到的作业能耗数据的误差,如图8所示。

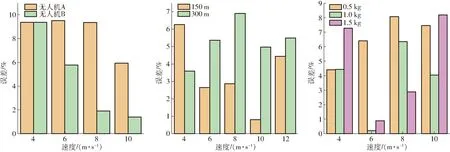
图8 理论计算和试验作业能耗的误差Fig.8 Errors of theoretical calculations and experimental operational energy consumption for three groups

将所得到的误差数据绘制为箱线图,如图9所示,由均值点可得,速度组的平均误差约为6.582%,航程组的平均误差约为4.264%,载荷组的平均误差约为5.057%。由中位线可得,速度组的误差中位数约为7.654%,航程组的误差中位数约为4.7%。载荷组的误差中位数约为5.399%,可以看出在当前输入的动态参数下,该模型计算的结果不管是在平均误差还是误差中位数,都与实际数据结果相近,证明了模型的有效性。再将该模型与基于电池性能研究的黑盒模型的误差4.3%进行对比[7],虽然不及黑盒建模准确,但也表现出较高的准确度。

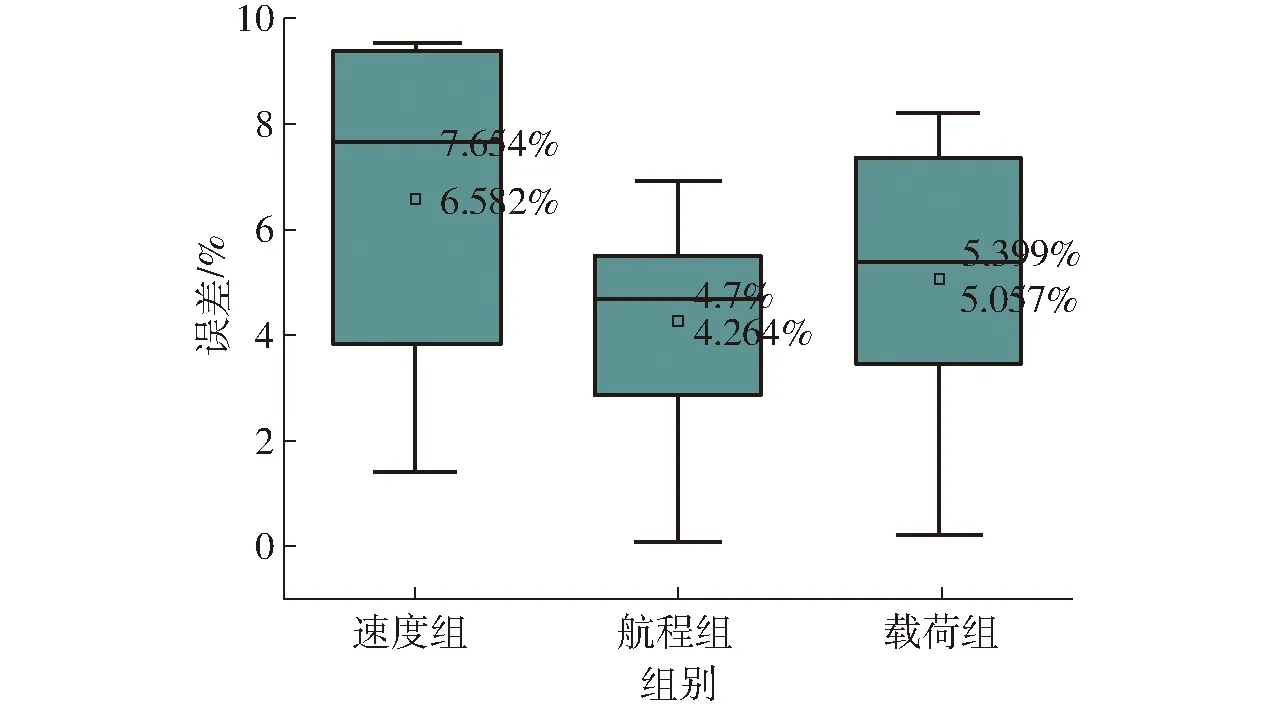
图9 理论计算和试验作业能耗误差箱线图Fig.9 Error box plots of theoretical calculations and experimental operational energy consumption for three groups

3.2 模型误差分析及修正方法

3.2.1模型误差分析

模型的误差分析主要是对模型的计算结果和主要参数进行进一步分析,公式(30)中总效率主要是从电池所提供电能的输入功率到螺旋桨所消耗机械能的输出功率转化关系,影响整个模型,总效率模型是由厂商提供的动力系统各个部件的理论参数计算的结果。公式(30)中P0主要影响无人机克服重力所做的功EG,也是由厂商提供的参数计算而来。这两个参数在模型中为固定值。

其次是对公式(30)中的阻力系数和无人机受空气阻力影响的有效面积进行分析,主要受环境风速和飞行速度影响,其中无人机受空气阻力影响的有效面积是由其俯视面的面积来估算,阻力系数为对应面积的阻力系数,以图10中无人机B的阻力能耗占作业能耗的百分比为例,这两个参数影响的作业能耗只占很小一部分,且试验时的环境风速如图4所示,大多数是轻风等级以下风速,轻风对无人机所受空气阻力影响很小,主要还是受到飞行速度影响,随着速度的增大,无人机的阻力所做功占作业能耗的比例逐渐增大。

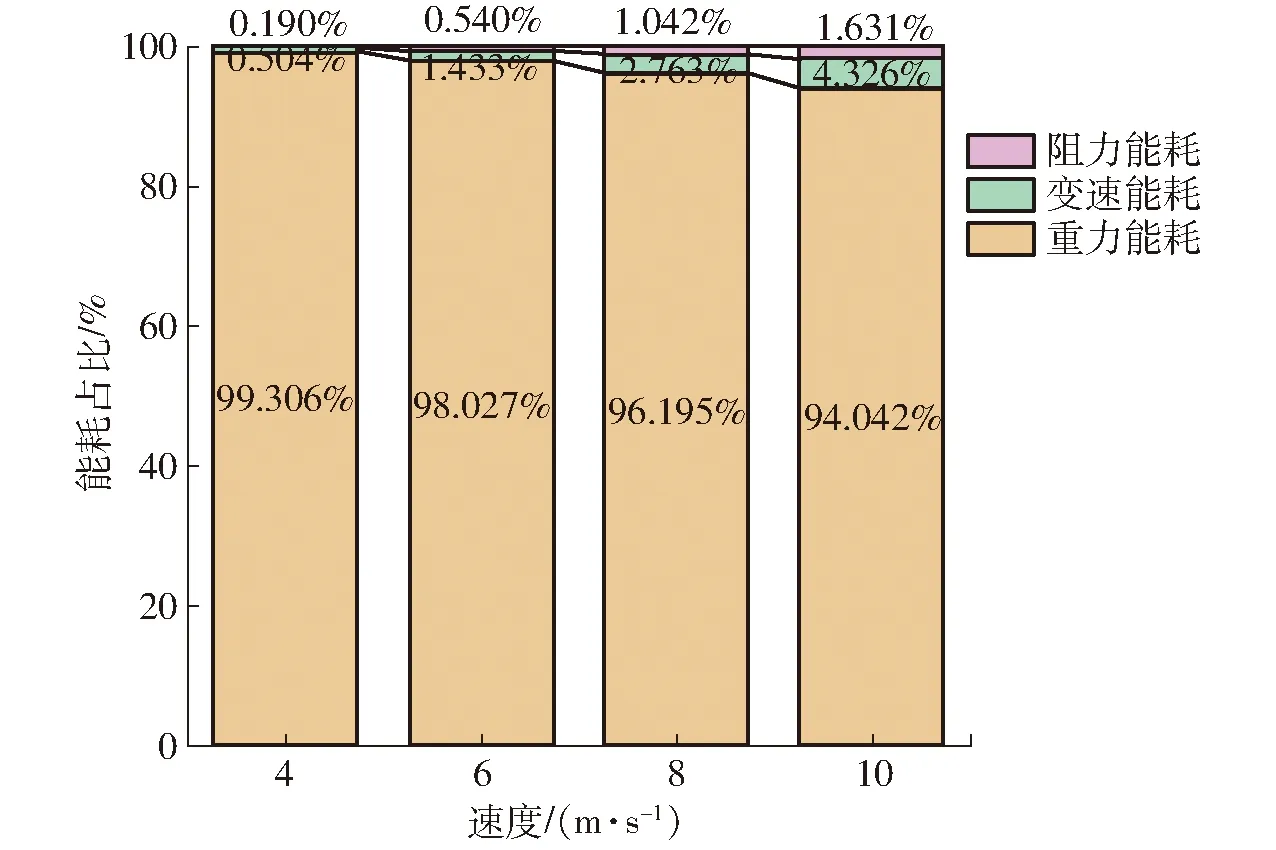
图10 无人机B的阻力所做功与作业能耗对比Fig.10 Comparison of resistance work and dynamic energy consumption of UAV

最后是对模型的速度和加速度参数进行分析,其中速度参数影响整个作业能耗,加速度影响无人机克服重力所做的功,这两个参数在理想模型中为定值。为了研究这两个参数对模型的影响,首先对环境风进行分析,在试验时环境风基本处于3.2 m/s,而在环境风速5 m/s下,在设定速度最高10 m/s的飞行速度下,环境风对无人机迎风倾角的影响可以忽略不计,而无人机倾角影响其飞行速度,所以在当前试验环境下,对加速度和速度的影响也可以忽略不计[29]。其次对机载采集设备采集的数据做进一步分析,在当前飞行控制器控制下,无人机在试验时由于本身存在控制误差,所以不能达到所需的速度。对于飞行控制器而言,不同控制策略会导致无人机不同的能量消耗[30],进而影响无人机飞行的作业能耗。对于飞行控制器而言,影响最大就是速度和加速度。原因有:①当前飞行控制器下,无人机在飞行时并不能达到预定的速度,而且设定速度越大时,其与实际的速度的误差越大,以无人机B的试验数据为例进行分析,如图11所示,匀速段的设定平均速度为4、6、8 m/s,但实际所达到的平均速度只有3.840 8、5.788 5、7.699 9 m/s,而对于设定平均速度为10 m/s的情况,实际的试验速度最高只达到约9.175 5 m/s。②在当前飞行控制器下,无人机在加速和减速航段中,也不能达到设定的加速度,同样以无人机B的试验数据为例进行分析,得到设定平均速度为10 m/s的4组试验加速减速段的平均加速度为0.867 9、0.853 4、0.871 1、0.836 3 m/s2,低于设定的平均加速段1 m/s2。

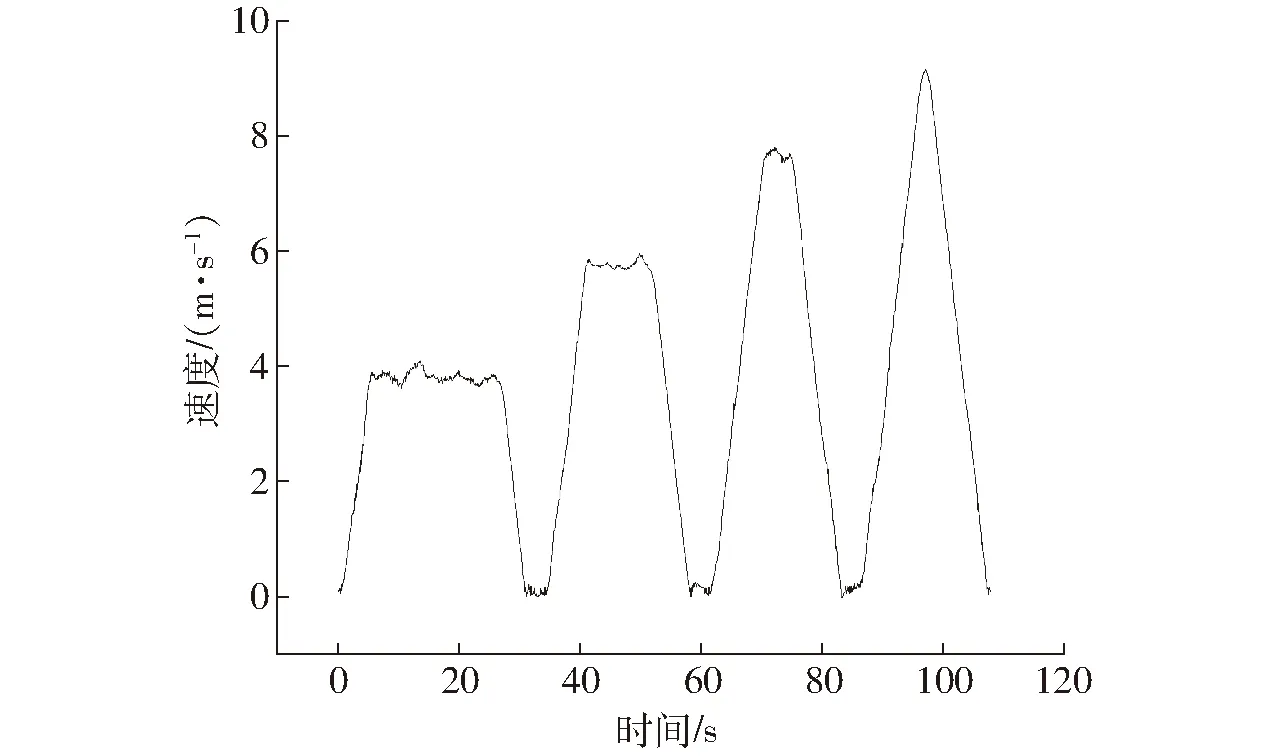
图11 无人机B的试验速度变化曲线Fig.11 Test speed of UAV

综合以上对模型各个参数的分析,模型的总效率和功率由厂商提供的参数计算得出,阻力系数和无人机受空气阻力影响的有效面积对模型结果影响较小,且主要是受速度参数影响,模型的速度和加速度参数对模型的结果影响较大,将主要对这两个参数进行修正。

3.2.2模型修正的方法及修正后结果对比

综合3.2.1节对模型各个参数进行分析的结论,对模型的速度和加速度参数进行修正,模型修正方法主要是引入修正系数来对模型的误差进行修正。然后针对速度和加速度输入参数引入速度和加速度修正系数来修正模型,对于飞行控制器,需要试验修正系数来修正该模型的输入参数,使得模型的输入参数更加接近当前飞行控制器的实际控制效果。

(32)

式中β——速度修正系数

γ——加速度修正系数

这两个修正系数需要对当前使用的飞行控制器输出进行分析,得到实际的速度和加速度,进而得到对应的修正系数。通过修正系数修正后的模型就可以得出更加准确的模型计算值和实际值之间的误差,以此来验证模型。

这两个修正系数的获取方法为:对于当前飞行控制器,根据采集得到北斗RTK数据的经纬度数据和时间数据,进而计算得出航程和时间,最后通过速度和加速度公式求出每一个匀速段的实际平均速度和实际平均加速度,得到两个输入参数的修正系数,如表3所示。

表3 所有组在不同航程下的实际平均速度、加速度及对应修正系数Tab.3 Actual average speed, acceleration and corresponding correction factor of all groups under different voyages

使用修正系数对模型的输入参数进行修正后,得到最终的作业能耗模型误差,如图12所示。从均值点可以看出,修正后速度组、航程组和载荷组相比修正前的平均误差减小约2.701、-1.118、3.092个百分点。从误差中位线可以看出,误差中位数减少约3.267、-1.617、3.612个百分点。修正模型输入参数后的模型也避免了因为飞行控制器带来输入参数误差的问题,保证模型的输入量更加接近于真实输入量,并且修正模型输入参数后的理论计算数据相比修正前更加接近于试验得到的数据。