干密度对邓肯-张模型参数的影响
2023-08-21郭江峰胡建林薛金昊房宇昊郑瑞海
郭江峰 胡建林,* 薛金昊 房宇昊 郑瑞海
(1.河北建筑工程学院土木工程学院,河北 张家口 075000;2.河北省沥青路面工程固废综合利用技术创新中心,河北 张家口 075000)
0 引 言
目前,描述土体应力-应变关系的数学模型有很多种,总体可以概括为两类:弹性模型和弹塑性模型[1].弹塑性模型能较好地反映土体的变形特征和内在机理以及土体的硬化、软化和剪胀特性,但参数获取难度较大.弹性模型中的非线性弹性模型简单实用[2],应用比较广泛.邓肯-张本构模型就是一种非线性弹性模型,可以较好的表征土的应力-应变关系.它采用修正各向同性广义胡克定律,本构关系为增量线性和各向同性,故应力和应变增量的主要方向是相同的,对于低应力水平较为实用,但对于应力水平较高或接近破坏时的偏差应力[3]存在一定的偏差,可以通过常规的三轴剪切试验获得邓肯-张模型的参数,从而可以推导出切线弹性模量,所以它被广泛应用于土体应力应变的研究.
在实际工程中取一些土样在室内进行固结排水三轴剪切试验,主要研究干密度对邓肯-张模型参数的影响,以便能够在实际工程中及时掌握该土质的性质和状态,从而解决工程中遇到的问题.根据试验得出的试验数据并进行分析整理以达到本文的研究目的.
1 邓肯-张模型的简介
邓肯-张模型[4]参数物理意义明确,易于确定,不考虑土体的应力历史,便于程序实施.邓肯(Duncan)和张(Chang)根据大量三轴试验得出的应力应变试验结果,提出土体的应力应变曲线应符合双曲线关系式的观点,其式可写成:
(1)
式中:(σ1-σ3)为偏应力,ε1为主应变;a值为初始切线变形模量Ei倒数;b值为极限偏差应力(σ1-σ3)ult的倒数,理论上是土样轴向应变无穷大时的应力差,但实际中轴向应变不可能无穷大.
试验中,土样破坏时对应的应力差称为破坏应力差,用(σ1-σ3)f表示;破坏应力差与极限偏差应力之比称为失效比Rf,Rf=(σ1-σ3)f/(σ1-σ3)ult;简布[5]研究发现,土体的初始弹性模量Ei与围压σ3存在指数关系,其式可表示为下式:
(2)
式中:Pa为大气压值,取101.4kPa,引入Pa是为了使纵横坐标化为无因次量.K、n为试验参数,可在lg(Ei/Pa)-lg(σ3/Pa)曲线中确定.土体的切线模量Et,可表示为:
(3)
式中:包含5个参数,C、φ为强度指标,另外三个K、n和Rf确定方法已作说明,其中Rf对不同围压会有不同值,取平均值即可.
2 试样制备及试验方案
2.1 土样的基本物理性质
本研究依托冀北地区的某大坝工程,取样深度距地表15~25m的粉质黏土土样进行试验.对不同干密度的土样试样进行三轴试验,实验测得土样的基本物理性质见表1.

表1 土样的基本物理性质
2.2 试样的制备
通过实验得该土样的最大干密度为1.78g/cm3,最优含水率为16.4%.研究不同干密度对邓肯-张模型中参数的影响[10],将土样的含水率按最优含水率配制,然后放入恒温养护箱内养护24h,以使土颗粒和水充分融合.按击实实验的制作方法在制样器内制作试验试件,试件的尺寸为3.91×8.0cm(直径×高),将制好的试件放入养护缸内,防止水分挥发对实验结果造成影响,试验试件控制的干密度分别为1.66g/cm3、1.69g/cm3、1.72g/cm3、1.75g/cm3.
2.3 试验方案
试验围压分别是100kPa、200kPa、300kPa、400kPa.剪切速率为0.65%/min.试验按照《土工试验方法标准》[6]进行固结排水试验,在试验中认为试样的破坏的标准为:当剪应力出现峰值时,再继续剪3%的主应变,试验结束;若无峰值出现,主应变达到15%后试验结束,取主应变为15%时的剪应力值为破坏剪应力值.
3 试验结果及计算
将试验结果进行处理和分析可得各不同干密度条件下的主应力差(σ1-σ3)与主应变ε1之间的关系,如图1所示.

a)干密度1.75g/cm3 b)干密度1.72g/cm3

c)干密度1.69g/cm3 d)干密度1.66g/cm3图1 不同干密度下(σ1-σ3)与ε1关系曲线
由图1绘出在不同干密度下该土体的摩尔应力圆,见图2,由图2得出在不同干密度下土体的粘聚力C和内摩擦角,见表2,由表2可以得出土体的C和均随着干密度的增加而增加.

a)干密度1.75g/cm3 b)干密度1.72g/cm3

c)干密度1.69g/cm3 d)干密度1.66g/cm3图2 不同干密度下土体的莫尔圆
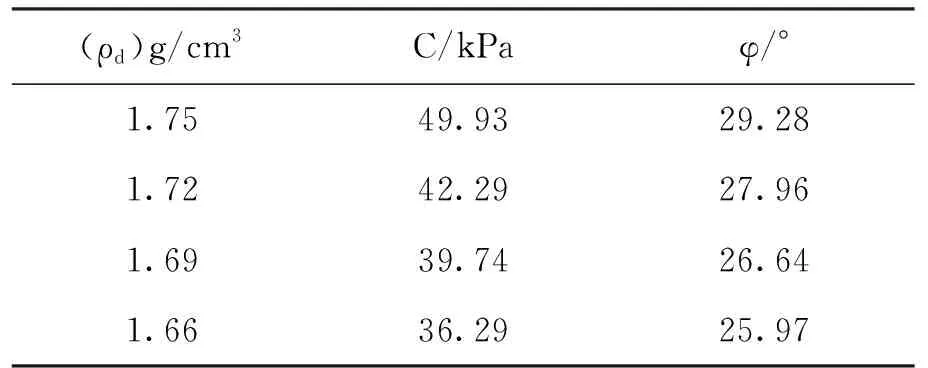
表2 不同干密度下的C、φ值
将式(1)改写成下式(4):
(4)
从式(4)中可以看出ε1/(σ1-σ3)呈线性关系,a、b分别为直线的截距和斜率,将(σ1-σ3)-ε1应力应变关系转换成ε1/(σ1-σ3)直线关系时,所得的线性关系有所偏差,所以在求取a、b值时,以应力水平S为75%及95%的点来求得a、b的值[7],应力水平S为主应力差(σ1-σ3)与破坏应力差(σ1-σ3)f的比值.以干密度为1.75g/cm3为例,得到各个围压下ε1/(σ1-σ3)-ε1的关系,见图3.

图3 各围压下ε1/(σ1-σ3)-ε1关系曲线
各个围压下的a、b值由图3可求得,然后得出Ei、(σ1-σ3)ult、Rf的值,见表3.

表3 各围压下的Ei、Rf参数值
由表3可求得表4中的数值.

表4 lg(Ei/Pa)-lg(σ3/pa)数值
由表4可以绘出lg(Ei/Pa)-lg(σ3/pa)的曲线图,见图4.

图4 K、n值的确定
由图4可以得出K=125.5741、n=0.6054.
干密度为1.75g/cm3时,切线弹性模量中的5个参数都已经求出,同法可得其它干密度条件下的各个参数值,见表5.

表5 各个干密度下的参数值
4 结 论
从试验所得的应力应变曲线可以看出,粉质黏土的抗剪强度随着干密度ρd增加而增大,当干密度为1.75g/cm3时土体的抗剪强度最高,最后趋于屈服,土样屈服前的抗剪强度的上升速率也随着干密度的增大而变的越来越快;随着围压的增大,应力-应变曲线表现为应变硬化型.
由表5可知K、n等参数也随着干密度的增加而增大,而破坏比Rf却有减小的趋势.在工程实际应用中比较关注的土的粘聚力C和内摩擦角φ也随着干密度ρd的增加而增大.
