随机七边形链中两类拓扑指数的期望值研究
2023-08-21孙玉霜耿显亚
孙玉霜,耿显亚
(安徽理工大学 数学与大数据学院,安徽 淮南 232001)
本文所考虑的都是有限简单图,设G=(V(G),E(G))是一个图,V(G)表示图的顶点集,E(G)表示图的边集,对于一个顶点v∈V,图G-u是由V-{u}给定的,对于一条边e,图G-e是由一个图G删去一条边e给定的[1-8],另外N(v)={u|uv∈E}表示在G中与v有边相连的点,NG[v]={v}∪N(v)表示与v有边连接的点且点v包括在内[3,11,15].

在后续计算中,我们会用到如下公式:
1) Gutman and Polansky[9],如果uv是G中的一条边,则
m(G)=m(G-uv)+m(G-{u,v})
(1)
2) Gutman and Polansky[9],如果v是G中的一个顶点,则
i(G)=i(G-v)+i(G-NG[v])
(2)
3) Gutman and Polansky[9],如果G是由G1,G2,…,Gk组成,则
(3)
4)m(p2)=2,m(p3)=3,m(p4)=5,m(p5)=8,m(p6)=13,m(C7)=29.
5)i(p1)=2,i(p2)=3,i(p3)=5,i(p4)=8,i(p5)=13,i(P6)=21.
其中:Pn表示n个顶点的路,Cn表示n个顶点的圈.
Gn可以视为具有n个七边形的链,也可以表示为末端有一个七边形的,如图1所示.

图1 有个七边形的链Figure 1 A chain with a hexagon


图2 七边形链的三种排列方式Figure 2 Three arrangements of heptagonal chain
一个有n个七边形的随机链Gn(p1,p2,p3)在之后的每一步k=(3,4,…,n)中都会有三种随机排列:



其中:p1,p2,p3是常数,与k无关.特别的,当p1=1,p2=1,p3=1时,图Gn分别可记为邻链Qn,元链Mn,对链Ln.
1 在随机七边形链中Hosoya指数的期望值探究


图3 末端连接的三类连接方式Figure 3 Three types of end connection
m(Gn)=m(Gn-e)+m(Gn-{u,v})=m(C7)m(Gn-1)+m(P6)m(An-2)=29m(Gn-1)+13m(An-2)

m(An-2)=m(P6)m(Gn-2)+m(P5)m(An-3)=13m(Gn-2)+8m(An-3)

m(An-2)=m(P6)m(Gn-2)+m(P5)m(Bn-3)=13m(Gn-2)+8m(Bn-3)

m(An-2)=m(P6)m(Gn-2)+m(P5)m(Cn-3)=13m(Gn-2)+8m(Cn-3)
m(Gn)=m(C7)m(Gn-1)+m(P6)m(Bn-2)=
29m(Gn-1)+13m(Bn-2)

m(Bn-2)=m(p6)m(Gn-2)+m(p1)m(p4)m(An-3)=
13m(Gn-2)+5m(An-3)

m(Bn-2)=m(p6)m(Gn-2)+m(p1)m(p4)m(Bn-3)=
13m(Gn-2)+5m(Bn-3)

m(Bn-2)=m(p6)m(Gn-2)+m(p1)m(p4)m(Cn-3)=
13m(Gn-2)+5m(Cn-3)
m(Gn)=m(C7)m(Gn-1)+m(p6)m(Cn-2)=
29m(Gn-1)+13m(Cn-2)

m(Cn-2)=m(p6)m(Gn-2)+m(p2)m(p3)m(An-3)=
13m(Gn-2)+6m(An-3)

m(Cn-2)=m(p6)m(Gn-2)+m(p2)m(p3)m(Bn-3)=
13m(Gn-2)+6m(Bn-3)

m(Cn-2)=m(p6)m(Gn-2)+m(p2)m(p3)m(Cn-3)=
13m(Gn-2)+6m(Cn-3)
根据式(1)~(3)且p1+p2+p3=1可以得到期望:
E(m(Gn))=29E(m(Gn-1))+13p1E(m(An-2))+
13p2E(m(Bn-2))+13p3E(m(Cn-2))=
29E(m(Gn-1))+169E(m(Gn-2))+
显然有
8p1E(m(An-4))+8p2E(m(Bn-4))+
8p3E(m(Cn-4))
5p1E(m(An-4))+5p2E(m(Bn-4))+
5p3E(m(Cn-4))
6p1E(m(An-4))+6p2E(m(Bn-4))+
6p3E(m(Cn-4))
根据上式,可分别得到
8p1[E(m(Gn-1))-29E(m(Gn-2))-
169E(m(Gn-3))]
5p2[E(m(Gn-1))-29E(m(Gn-2))-
169E(M(Gn-3))]
6p3[E(m(Gn-1))-29E(m(Gn-2))-
169E(m(Gn-3))]
综上所述且根据p1+p2+p3=1即得关于Hosoya指数期望值的递推公式:
E(m(Gn))=(29+8p1+5p2+6p3)E(m(Gn-1))+
(169-232p1-145p2-174p3)E(m(Gn-2))=
(2p1-p2+35)E(m(Gn-1))-
(58p1-29p2-5)E(m(Gn-2))
另外,期望值存在两个极限:
E(m(G1)) =m(C7)=29E(m(G2))=1 010
利用上述递推关系和边界条件,我们可以得到:
定理2.1 在随机七边形链中Hosoya指数的期望值
E(m(Gn))=
分别令p1=1,p2=1,p3=1我们可以从定理2.1中得到On,Mn,Ln的Hosoya指数的推论.
推论2.2
2 在随机七边形链中Merrifield-Simmons指数的期望值探究
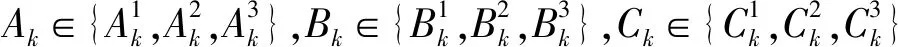
i(Gn)=i(Gn-v)+i(Gn-NG[v])=
i(P6)i(Gn-1)+i(P4)i(An-2)=
21i(Gn-1)+8i(An-2)

i(An-2)=i(P5)i(Gn-2)+i(P4)i(An-3)=
13i(Gn-2)+8i(An-3)

i(An-2)=i(P5)i(Gn-2)+i(P4)i(Bn-3)=
13i(Gn-2)+8i(Bn-3)

i(An-2)=i(P5)i(Gn-2)+i(P4)i(Cn-3)=
13i(Gn-2)+8i(Cn-3)
i(Gn)=i(P6)i(Gn-1)+i(P4)i(Bn-2)=
21i(Gn-1)+8i(Bn-2)

i(Bn-2)=i(p1)i(p4)i(Gn-2)+i(p3)i(An-3)=
16i(Gn-2)+5i(An-3)

i(Bn-2)=i(p1)i(p4)i(Gn-2)+i(p3)i(Bn-3)=
16i(Gn-2)+5i(Bn-3)

i(Bn-2)=i(p1)i(p4)i(Gn-2)+i(p3)i(Cn-3)=
16i(Gn-2)+5i(Cn-3)
i(Gn)=i(P6)i(Gn-1)+i(P4)i(Cn-2)=
21i(Gn-1)+8i(Cn-2)

i(Cn-2)=i(P2)i(P3)i(Gn-2)+
i(P1)i(P2)i(An-3)=15i(Gn-2)+6i(An-3)

i(Cn-2)=i(P2)i(P3)i(Gn-2)+
i(P1)i(P2)i(Bn-3)=15i(Gn-2)+6i(Bn-3)

i(Cn-2)=i(P2)i(P3)i(Gn-2)+
i(P1)i(P2)i(Cn-3)=15i(Gn-2)+6i(Vn-3)
根据式(1)~(3)且p1+p2+p3=1可以得到期望:
显然有
E(i(Gn))=21E(i(Gn-1))+(104p1+128p2+
48p2p3)E(i(Bn-3))+(64p1p3+40p2p3+
8p2E(i(Bn-4))+8p3E(i(Cn-4))
5p2E(i(Bn-4))+5p3E(i(Cn-4))
6p2E(i(Bn-4))+6p3E(i(Cn-4))
根据上式,可分别得到
8p1[E(i(Gn-1))-21E(i(Gn-2))-
(104p1+128p2+120p3)E(i(Gn-3))]
5p2[E(i(Gn-1))-21E(i(Gn-2))-
(104p1+128p2+120p3)E(i(Gn-3))]
6p3[E(i(Gn-1))-21E(i(Gn-2))-
(104p1+128p2+120p3)E(i(Gn-3))]
综上所述且根据p3=1-p1-p2可以得到关于Merrifield-Simmons指数期望值的递推公式:
E(i(Gn))=(21+8p1+5p2+6p3)E(i(Gn-1))+
(-64p1+23p2-6p3)E(i(Gn-2))=
(2p1-p2+27)E(i(Gn-1))-
(58p1-29p2+6)E(i(Gn-2))
E(i(G1))=i(C4)=7E(i(G2))=777
利用上述递推关系和边界条件,可以得到:
定理3.1 在随机七边形链中Merrifield-Simmons指数的期望值
E(i(Gn))=
分别令p1=1,p2=1,p3=1,我们可以从定理3.1中得到On,Mn,Ln的Merrifield-Simmons指数的推论:
推论3.2
3 结 语
本文得到了含有n个七边形的随机链的Hosoya指数Merrifield-Simmons指数的期望值的具体推导解析公式,并分别讨论了m(Gn)和i(Gn)的期望值,它们的组成和结构也正在向图论的相关研究方向发展.
