基于无单元局部弱式法的2.5维直流电阻率正演

麻昌英，闫玲玲，姚振岸*，柳建新，赵文学，周聪

（1.江西省防震减灾与工程地质灾害探测工程研究中心（东华理工大学），江西南昌 330013； 2.中南大学有色金属成矿预测与地质环境监测教育部重点实验室，湖南长沙 410083； 3.东华理工大学地球物理与测控技术学院，江西南昌 330013）

0 引言

目前直流电阻率法正演模拟主要采用积分方程法、有限差分法和有限单元法（Finite element method，FEM）。相比积分方程法和有限差分法，FEM 的优势是适应于任意地形和任意复杂的地质目标的模拟，具有适应性强、精度高、计算效率较高等特点，是目前直流电阻率法和电磁法正演模拟中主要的数值模拟方法［1-10］。近年来，在常规FEM 基础上，基于非结构化单元和自适应加密策略的自适应FEM 得到了快速发展［11-24］。自适应FEM 利用图形几何学相关单元剖分器对任意分布节点进行网格剖分。非结构化单元适用于起伏地形和地下形态复杂目标体的正演模拟，可在局部区域自适应地加密单元，模拟过程更灵活，具有较高的模拟精度。基于非结构化单元的FEM 可很好地模拟复杂起伏地形和地下复杂目标体，但不规则单元剖分不可避免。由于使用预定义的、基于节点连接信息的单元进行模拟，不可避免地需要进行网格单元剖分［25-28］。随着计算机硬件的快速发展，以及野外实际生产中待开发区域地质条件日趋复杂，对资料解释及勘探精细化的要求不断提高，尤其对复杂地电模型的模拟灵活性和模拟精度需求更高。发展创新型的精细化、高灵活性和更高模拟精度的地球物理勘探数据解译系统，已成为地球物理勘探领域的研究热点。

相比传统数值模拟方法，基于全局弱式的无单元Galerkin 法（Element-Free Galerkin Method，EFGM）无需进行基于节点连接信息的单元剖分［29］，可方便地根据实际需求任意布置和加密节点，对任意复杂地电模型及局部加密等问题具有很强的适应性，是一种高灵活性、高精度的正演模拟方法［30-33］。在地球物理领域，无单元Galerkin 法在地震波场［34-40］、探地雷达［27，41-42］、大地电磁［43-47］及重力勘探［48-49］等正演模拟研究中取得了良好的研究成果。在直流电阻率法正演模拟中，麻昌英等［50-51］、Ma 等［52］分别利用径向基点插值（RPIM）形函数和移动最小二乘（MLS）形函数开展了2.5维直流电阻率EFGM 正演，实现了任意复杂形体、地形起伏、局部节点加密的直流电阻率法的正演模拟。研究成果表明，EFGM 能有效地解决传统数值模拟方法受单元约束的局限性，与传统数值模拟方法相辅相成，具有较高的灵活性、适应性和模拟精度，尤其在任意复杂地电模型的正演中效果很好，在地球物理领域具有良好的发展前景。

EFGM 是一种基于全局弱式的无单元法，需要借助于全局域剖分背景单元进行积分计算，对单元仍有一定的依赖性，一定程度上损失了无单元的属性。为进一步减小对单元的依赖性，避免使用全局域背景单元积分，基于局部弱式的无单元法得以快速发展。Atluri 等［53］在弹性静力学局部边界积分方程的基础上，提出了无网格局部Petrov-Galerkin 法（Mesh-Free Local Petrov-Galerkin Method，MLPGM）。该方法利用加权余量法，将全局域积分转化为节点局部域积分。MLPGM 应用于大地电磁场的二维正演模拟［28，54］，展现了较强的灵活性和适应性及较高的计算精度。然而，与EFGM 引入权函数不同，MLPGM 采用加权余量法进行方程离散，使用了更多的模拟参数；同时，离散方程按节点编号进行组装，系数矩阵稀疏但不对称。Melenk 等［55］和Babuška 等［56］提出了单位分解有限单元法（Partition of Unity Finite Element Method，PUFEM）和单位分解法（Partition of Unity Method，PUM），并进行了严格的数学证明和论述；Carpinteri等［57］将PUM 积分应用于EFGM，将全局域积分转化为节点局部域积分，实现了基于局部弱式的无单元法。随后，该方法在各个领域得到深入研究和广泛的应用［58-62］。基于局部弱式的无单元法与EFGM 类似，计算过程基本一致，均继承了FEM 的一些优点，形成稀疏对称的系数矩阵；但基于局部弱式的无单元法利用了单位分解积分将全局域积分转化为节点局部域积分，摆脱了背景单元的限制，是一种真正的无单元法，具有更高的灵活性和更强的适应性。

本文基于戴前伟等［41］、Feng 等［42］、麻昌英等［50］、Ma 等［52］提出的探地雷达和直流电阻率EFGM 正演方法，将单位分解积分应用于直流电阻率EFGM 正演，提出直流电阻率无单元局部弱式法（Local Weak Form Element-Free Method，LWF-EFM），实现了高灵活性、高精度的2.5 维直流电阻率正演模拟。将上述方法分别应用于层状模型及二维异常体模型的正演模拟，验证了本文算法的有效性，结果表明本文方法相比于FEM 和无单元Galerkin 法具有更强的灵活性和更高的模拟精度，可为高精度直流电阻率资料解释提供技术支持。

1 直流电阻率法2.5 维边值问题的全局弱式形式

当采用第三类边界条件时，2.5 维直流电阻率法波数域总电位U(x，λ)的边值问题及变分问题可分别表示为［63］

式中：σ表示电导率；λ表示波数；I0表示电流；δ(A)表示狄拉克函数，其中A是场源点；K0、K1分别表示第二类零阶、一阶修正贝塞尔函数；Ω表示问题域（全局域）；Γs表示地表边界，Γ∞为截断边界；rA为场源点A到截断边界的距离；n为边界上的单位外法向；cos(rA，n)表示n与矢径rA构成的夹角余弦。式（2）经EFGM 推导可获得基于全局弱式的三项积分式K(1)、K(2)和F［50-52］

式中ΦT=[ϕ1，ϕ2，…，ϕn]为形函数向量，其中n表示支持域Ω中的场节点个数。不同正演方法采用不同的形函数。在无单元法中可采用径向基点插值法（Radial Point Interpolation Method，RPIM）形函数［50-51］和移动最小二乘（Moving Least Squares，MLS）形函数［52］；FEM 则采用基于单元构造的形函数，这些形函数均具有单位分解性质。由于RPIM 形函数具有Kronecker delta 函数性质、数值稳定性较好、适应性强等优点，本文采用RPIM 形函数进行正演计算。采用单位分解积分法可将式（3）～式（5）中的全局域积分转化到局部积分域求解。

2 单位分解积分

覆盖和单位分解是单位分解积分［25，56］的基础。设Ω是定义在Rd(d=1，2，3)上的有界开域，表示Ω的闭包，QN表示Ω中N个点的集合

基于QN定义有限开覆盖，表示N个中点在xk(k=1，2，…，N)的圆域（或矩形域），满足

则称ON是Ω的一个有限覆盖。式（7）中rk为点xk(k=1，2，…，N)对应的覆盖Ωk的半径。如图1 所示，在有界区域Ω内由有限个节点xk(k=1，2，…，N)对应的构成了Ω上的一个有限覆盖。

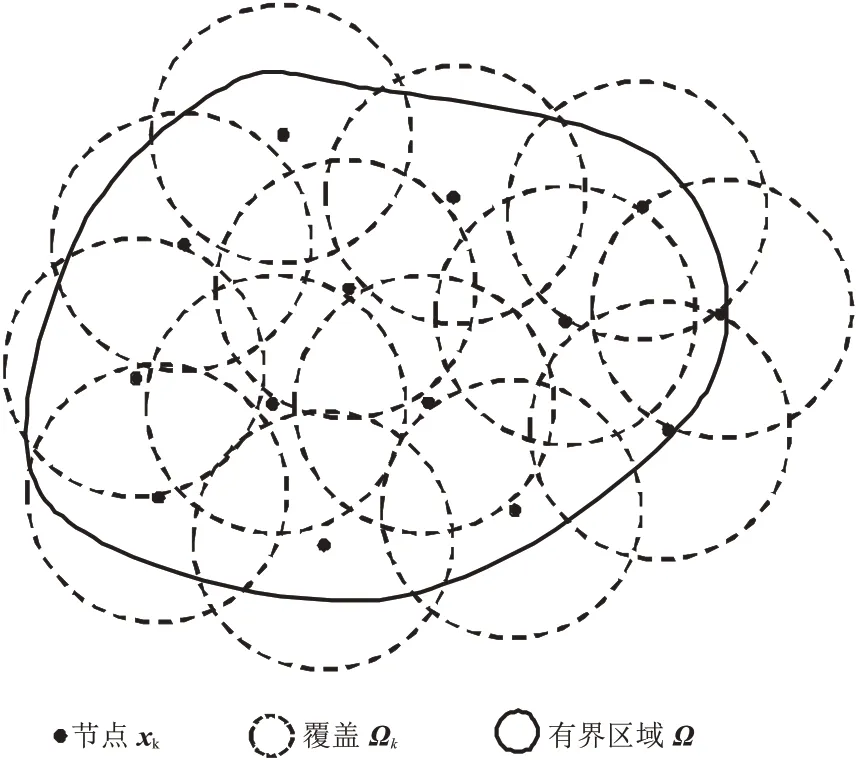
图1 有限覆盖示意图

由于式（12）具有单位分解的性质，因此称这种积分方式为单位分解积分（Partition of Unity Quadrature，PUQ）。式（12）是单位分解积分的基础，通过该式可将有界区域Ω（包含边界）上的积分转化成节点子域Ωk上的积分之和。若将单位分解积分应用到式（3）～式（5），则积分式将用到两个函数集：形函数Φ(x)和单位分解函数Ψ(x)。单位分解函数和形函数在本质上是两个不同的函数系，两者相互独立，任意具有单位分解性质的函数，均满足式（9）～式（11），因此都可作为单位分解函数。由单位分解积分定理可知，单位分解函数不会对积分计算精度产生影响。由于形函数（如RPIM、MLS、FEM 形函数等）均具有单位分解性质，在求解域Ω内任意一点的形函数之和为1，即

即形函数Φ(x)满足式（9）～式（11），因此本文将正演方法中构造的形函数Φ(x)作为单位分解函数，即

其中ϕk(x)为计算点对节点k的形函数。

3 直流电阻率法2.5 维LWF-EFM正演

3.1 节点局部积分域构造

在LWF-EFM 中，首先需要为每一个节点构造节点局部积分域，目的是将全局域积分转化为节点局部域积分；然后，计算域Ω中的集合QN={x1，x2，…，xN}，xk∈Ω，以节点xk(k=1，2，…，N)为中心构造计算域Ω的一个有限覆盖，覆盖Ωk的形式可以是圆形、椭圆形、矩形等。由式（12）可知，通过单位分解积分，可将全局域Ω积分转化为节点局部域Ωk(k=1，2，…，N)的积分之和，其中节点局部积分域即为节点的覆盖，因此覆盖构造即为节点局部积分域构造。为了方便布置高斯点进行积分计算，本文采用矩形节点局部积分域。对于矩形节点局部积分域，在二维情况下通常采用两个方向的尺寸参数确定范围。下面以直流电阻率数据为例，说明LWF-EFM 矩形节点局部积分域的确定方法。

对于一个节点，其节点局部积分域的尺寸ds为

式中：αs为积分域的无量纲尺寸，一般选1.0～3.0，可通过数值试验选取；p为节点局部积分域内节点间的平均距离，当节点均匀分布时，p取相邻两节点间的距离，节点非均匀分布时，p取节点积分域内结点平均距离。一维情况下，定义平均节点距离为

式中：Ds为ds的预估值；nDs为积分域内预估节点数。二维情况下，节点平均距离定义为

式中：S为积分域的预估面积；nS为积分域内预估节点数。二维情况下，ds可使用两个坐标方向表示

式中：ds=[dsxdsz]；αsp=[αsxpxαszpz]。矩形节点局部积分域如图2所示。

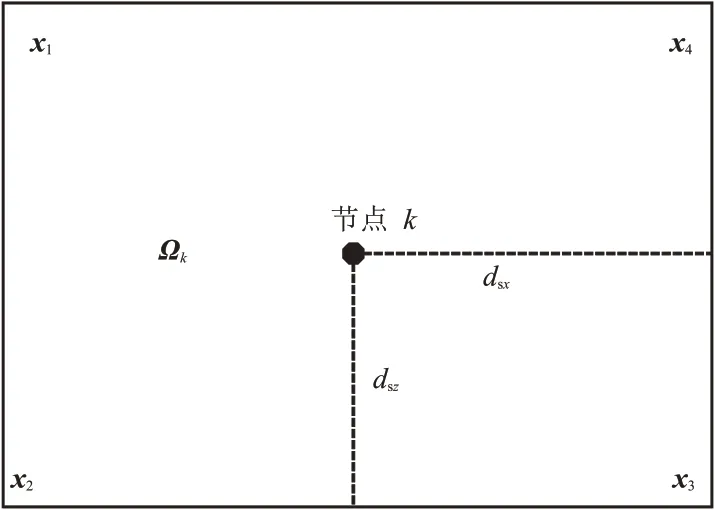
图2 矩形节点局部积分域示意图

图2 中节点k的坐标为xk=(xk，zk)，则矩形节点局部积分域的四个顶点坐标为

如果该矩形节点局部积分域超出了全局计算域，则应将矩形节点局部积分域划在计算域内，超出计算域Ω的部分应去掉。当域Ω的边界为矩形时，边界上矩形节点局部积分域顶点坐标为

其中：x1，x2＜xmin；x3，x4＞xmax；z1，z4＜zmin；z2，z3＞zmax。

为保证数值积分的计算精度，通常将节点局部积分域进一步划分成ndx×ndz个子域，然后对每个子域单独布置高斯积分点，计算积分并求和。例如：当ndx=ndz=2 时，采用4 个子域，节点局部积分域细分方案如图3所示。

图3 ndx=ndz=2 时节点局部积分域再划分子域示意图

第i（i=1，2，…，ndx×ndz）个子域的四个顶点坐标分别为

式中：dnx=(x4-x1)/ndx；dnz=(z2-z1)/ndz。

由于采用节点局部积分域计算，在地形起伏区域内地表上的节点积分域与地形相交，靠近地表的节点局部积分域也可能与地形相交，对地形以外的区域不需要进行积分计算，特别是地形起伏形态复杂时，需要对该部分节点局部积分域进行特殊处理，使得计算区域更加贴合地形。为了更好地模拟计算域Ω的地表边界，当积分域落在计算域Ω地表边界之外时，可省略Ω之外的积分域，仅对Ω内和边界进行积分。根据上述节点局部积分域构造方法，可知节点局部积分域的大小与节点疏密程度成正相关，即在节点密集分布区域对节点局部积分域自适应缩小尺寸，反之则放大尺寸，可自动获得与节点分布相适应的一组节点局部积分域。因此，节点局部积分域越小，越有利于模拟地形形态，因此对节点局部积分域进一步细分有利于LWF-EFM 对地形起伏模型的精确模拟。

3.2 局部弱式无单元法正演

将单位分解积分式（12）分别代入式（3）和式（4），得到

应用单位分解积分法对原积分进行离散化后，将计算域Ω（包含边界Γ∞）上的全局域积分转化成节点局部积分域Ωk（包含边界）上的积分之和，即将全局弱式转化为局部弱式，完成了直流电阻率LWFEFM 的主要积分部分（图4）。为方便起见，本文采用圆形支持域［50-52］，即给定积分点（即高斯点）支持域内节点数nq后，按距离选取积分点最近的nq个节点作为该积分点的支持域。

图4 基于单位分解积分的无单元法求解示意图

假设节点局部积分域Ωk中采用了Ng个高斯点xg=(xg，zg)，g=1，2，…，Ng进行积分计算，高斯点xg对应的权重和雅可比值分别为wg和Jg，高斯点xg的支持域Ωq内包含nq个节点，则有

展开式（23）～式（25），得到

其中ϕi(i=1，2，…，nq)为高斯点xg支持域内nq个节点对应的形函数。对于单个节点xk和单个高斯点xg，有

上式为积分点子系数矩阵，其矩阵元素为

式中i，j=1，2，…，nq，表示支持域Ωq中的节点局部编号。

对于式（5），若采用N个节点对计算域Ω进行离散，可得

当无单元法形函数具有Kronecker delta 函数性质时，上式右端项为

当无单元法形函数不具有Kronecker delta 函数性质时，式（33）的右端项为

如图5 所示，当节点局部积分域相无不重叠且恰好覆盖计算域时，节点局部积分域内任意一点对应该节点的单位分解函数为1，这种情况即为基于全局弱式积分的数值模拟法，例如EFGM 和FEM。在EFGM 中节点局部积分域可视为背景积分单元，在FEM 中节点局部积分域可视为基于节点拓扑关系剖分的网格单元。相比于基于全局弱式的EFGM，LWF-EFM 在求解K(1)、K(2)两项积分式时不需要在全局域内剖分背景积分单元，是真正意义上的无单元法。

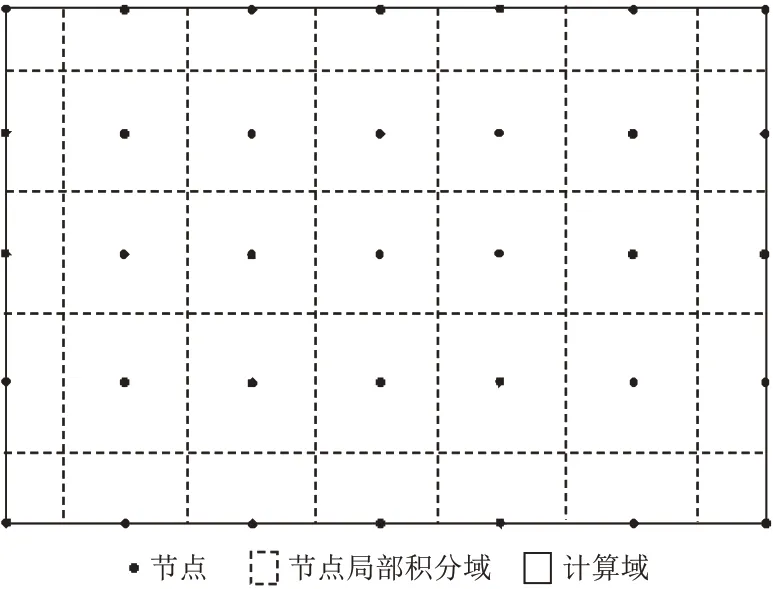
图5 节点局部积分域相互不重叠且恰好覆盖计算域示意图

4 模型算例

4.1 层状模型

采用具有解析解的三层电阻率模型（图6）验证直流电阻率LWF-EFM 算法的有效性。建立水平方向宽380 m（x：-190～190 m），垂直方向深108 m（z：0～108 m）的矩形计算域。在地表埋设52 根电极作为供电和观测电极，在地表x=0处进行对称四极装置测深观测。节点分布如图7 所示，对计算域采用不规则节点进行离散，靠近电极和地层界面区域节点密度较大，其他区域则采用稀疏的节点分布，总节点数为14280。分别采用LWF-EFM、EFGM 和FEM 对22组不同收发距（，其中表示电极A、B 间的距离）观测数据进行正演模拟。对于LWF-EFM，节点局部积分域以节点为中心分为4 个子积分域，即ndx=ndz=2，在子积分域中采用16 个高斯点，即G=16，支持域内使用4个节点。对于EFGM 模拟，背景单元内采用16个高斯点，即G=16，支持域内使用4个节点。

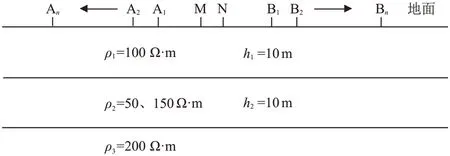
图6 层状模型及对称四极装置观测示意图

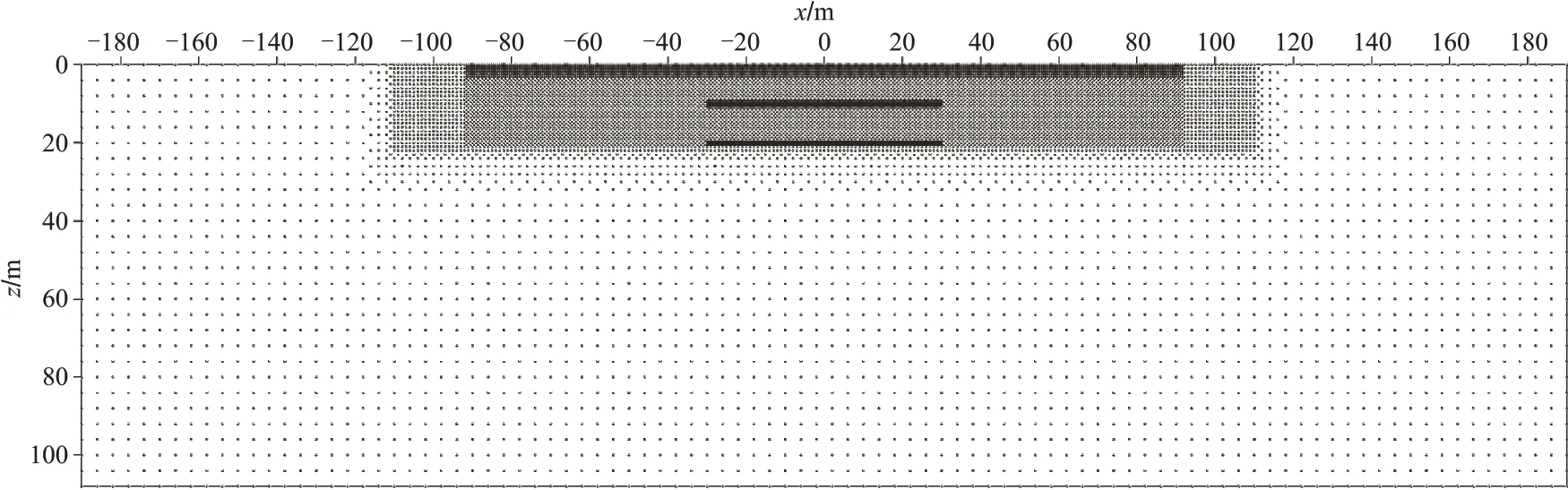
图7 层状模型节点分布示意图

图8 和图9 分别是ρ2为150、50 Ω·m 时的视电阻率和相对误差曲线。可以看出：无论中间层为高阻或低阻，LWF-EFM 的模拟结果与解析解均吻合较好，相对误差较小。表1 为模拟结果平均相对误差，可见LWF-EFM 模拟结果平均相对误差与EFGM 相差不大，均小于1%，低于FEM 平均相对误差，表明了LWF-EFM 的有效性。层状模型不同方法模拟结果分析表明，在计算域较小时，FEM 受到边界影响较大，EFGM 和LWF-EFM 可获得高精度的模拟结果。采用合适的模拟参数时，相比于FEM，LWF-EFM 可获得更高的模拟精度，与EFGM 模拟精度相当。

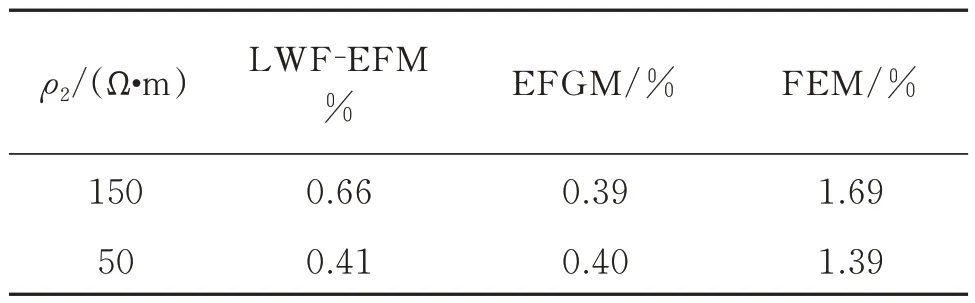
表1 层状模型不同方法视电阻率平均相对误差

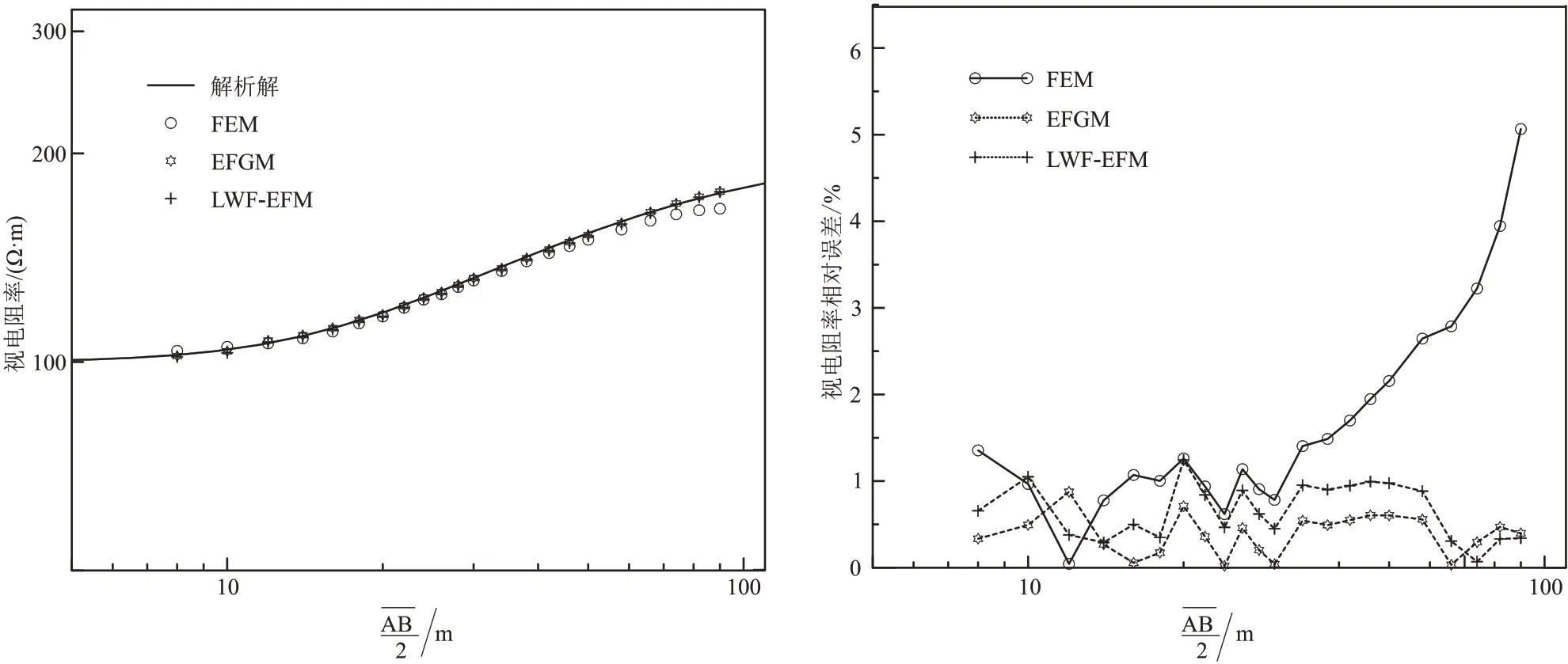
图8 层状模型ρ2=150 Ω·m 时不同方法模拟视电阻率（左）和相对误差（右）曲线

图9 层状模型ρ2=50 Ω·m 时不同方法模拟视电阻率（左）和相对误差（右）曲线

4.2 二维矩形异常体模型

建立一个均匀半空间模型，介质电阻率ρ1=100 Ω·m；在均匀半空间中有一个电阻率ρ2=1000 Ω·m的二维矩形异常体，异常体宽10 m（x方向），高8 m（z方向），中心点坐标（x，z）为（0，15 m）［52］。计算域Ω水平方向宽200 m（x：-100～100 m），垂直方向高100 m（z：0～100 m）。

分别采用三种类型节点分布离散计算域：第1种为均匀节点分布，节点间距为1 m，节点总数为20301；第2 种节点分布是在第1 种节点分布基础上，对靠近场源的浅层区域和异常体区域进行节点加密，节点总数为25150（图10a）；第3 种节点分布是在第2 种节点分布基础上，对计算域外围区域的节点进行抽稀，节点总数为12878（图10b）。在地表水平方向-58～58 m 范围内以2 m 的间隔均匀布置59 根电极，进行直流电阻率法温纳装置［64］观测。下文若不加以说明，均采用该电极布置和观测装置。为减小边界影响，采用FEM 进行正演模拟时，首先在第2 种节点分布基础上对计算域进行扩边，扩边后的范围为2000 m×1000 m；然后，分别使用第1种节点分布和第3 种节点分布，采用EFGM 和LWFEFM 进行正演模拟。EFGM 模拟采用1 m×1 m 的背景积分单元。这两种方法计算过程中，每个积分单元（或节点子局部积分域）均采用16 个高斯积分点。

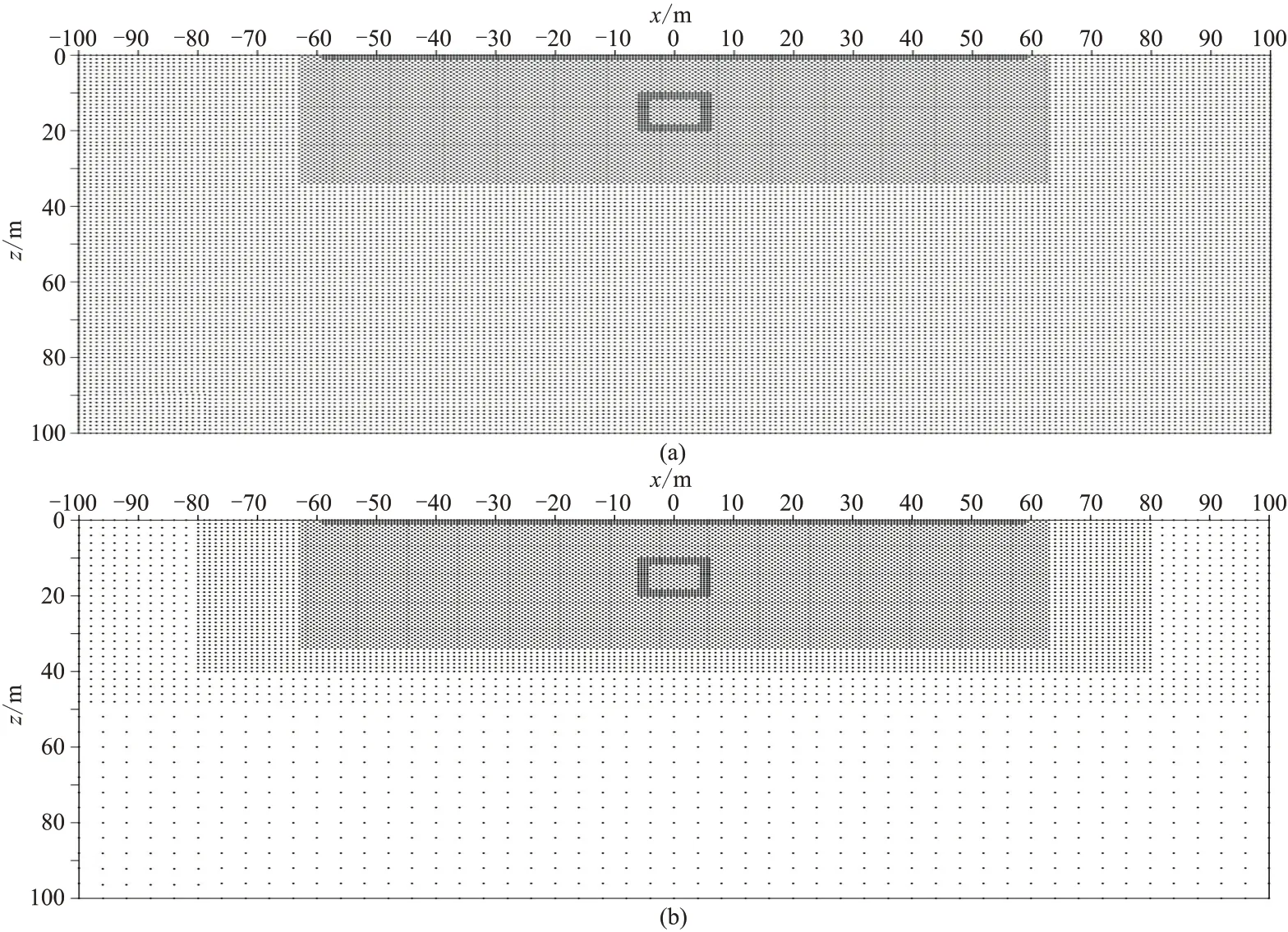
图10 二维模型模拟采用的剖分节点分布示意图［52］

图11为基于第2种节点分布、采用FEM 计算的电阻率拟断面。由于第2种节点分布相比于其他两种节点分布节点数最多，且在靠近场源和异常体周围区域进行了节点加密，因此该节点分布条件下的计算结果更精确，故将图11所示结果作为标准结果。图12a和图12b 为采用EFGM 获得的模拟结果，图12c 和图12d 为EFGM 模拟结果与参考标准结果的相对误差。对比图12c和图12d可知，使用第3种节点分布的相对误差较小，大部分区域相对误差接近0，而使用第1 种节点分布时，在浅层和异常体周围区域相对误差明显相对较大。

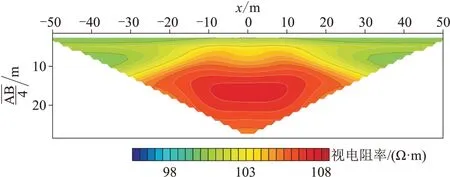
图11 二维模型基于第2 种节点的FEM 视电阻率拟断面

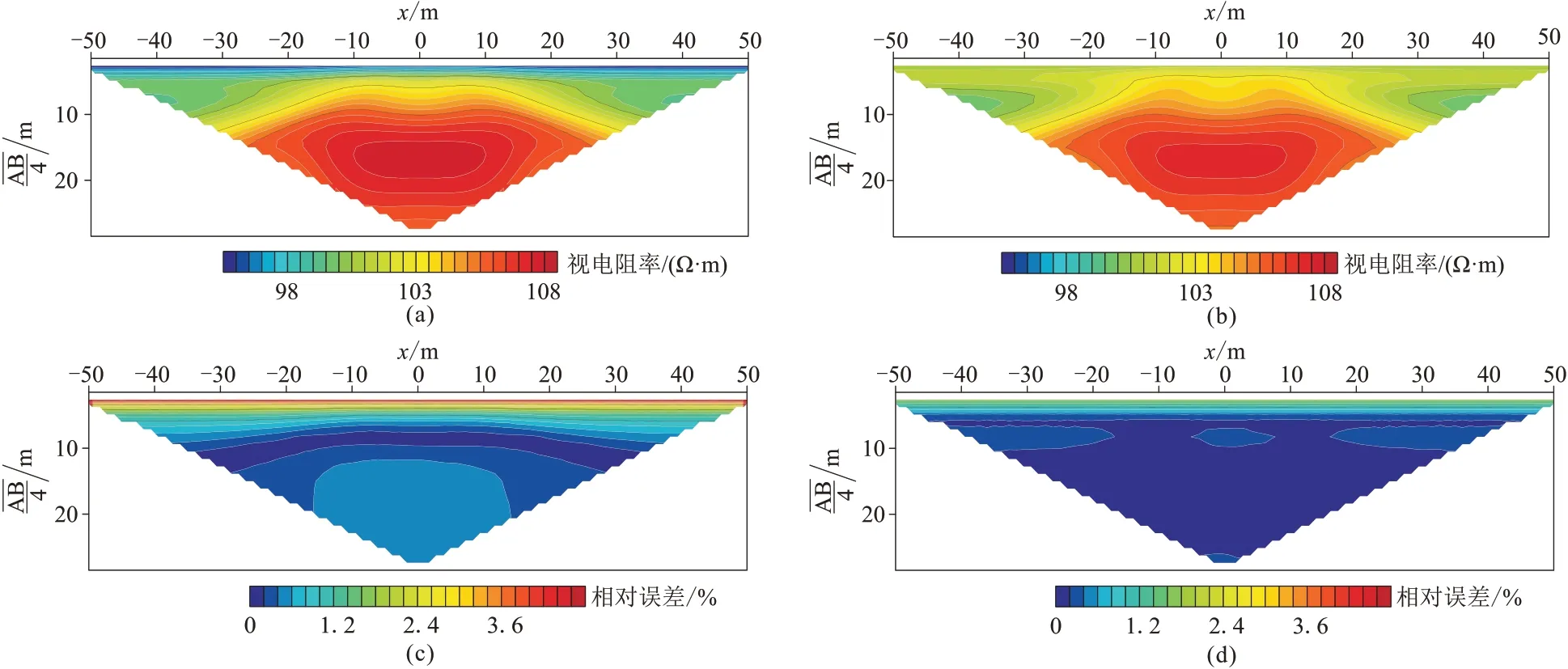
图12 二维模型EFGM 视电阻率拟断面（上）及相对误差剖面（下）

图13为采用LWF-EFM 获得的模拟结果。对比图13a、图13b与图11可知，LWF-EFM 的模拟结果与参考结果基本一致，表明LWF-EFM 模拟结果是可靠的。对比图13c和图13d 可知，与EFGM 类似，LWFEFM 使用第3 种节点分布得到的模拟结果相对误差较小，大部分区域相对误差接近0，而采用第1 种节点分布时，在浅层和异常体周围区域相对误差明显相对较大。

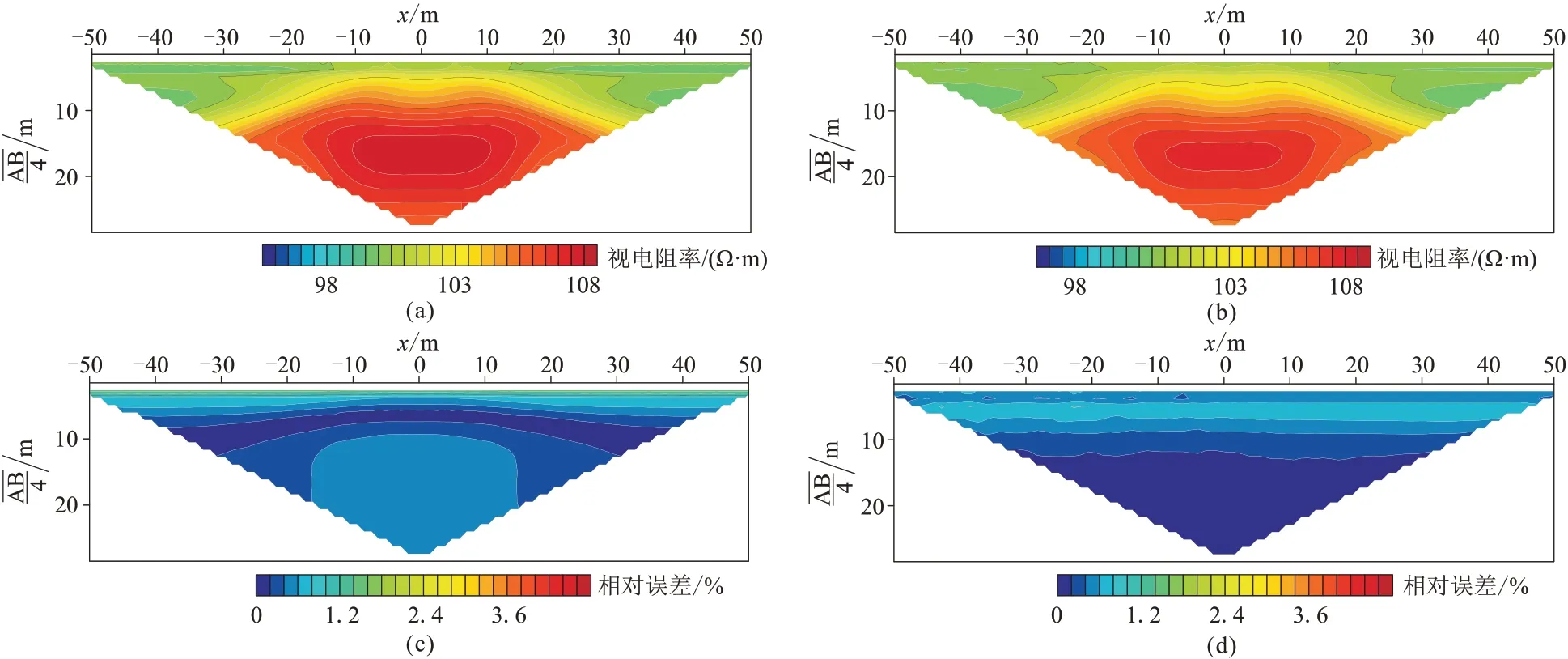
图13 二维模型LWF-EFM 视电阻率拟断面（上）及相对误差剖面（下）

表2为第1种和第2种节点分布的节点数、模拟结果最大相对误差、平均相对误差和计算时间统计。可知采用第1种节点分布时最大相对误差和平均相对误差均大于第3种节点分布；同时，由于第1 种节点分布使用了更多的节点，计算成本显著更高。对比相对误差统计结果可知，与EFGM 一样，LWF-EFM 也可采用不规则的节点分布，在场源和异常体周围区域加密节点，在计算域外围区域使用稀疏的节点分布，可在使用更少节点的条件下获得与均匀节点分布相同或更高的模拟精度；同时，使用更少的节点也可节省计算成本。相比EFGM，LWF-EFM 计算效率较低，主要原因是不同节点分布的节点局部积分域之间通常存在很多重合区域，实际计算积分面积大于计算域Ω，导致计算量增加。但由于采用节点局部积分域进行积分，仅需要设定节点局部积分域参数，不再需要背景单元剖分，相对需要背景单元的EFGM 对单元的依赖性更小，是真正的无单元法，正演过程更方便。同时，在计算域内任意区域进行节点加密或者稀释均十分方便，可根据节点分布情况自动构造节点局部积分域，无需其他处理，具有更高的灵活性。

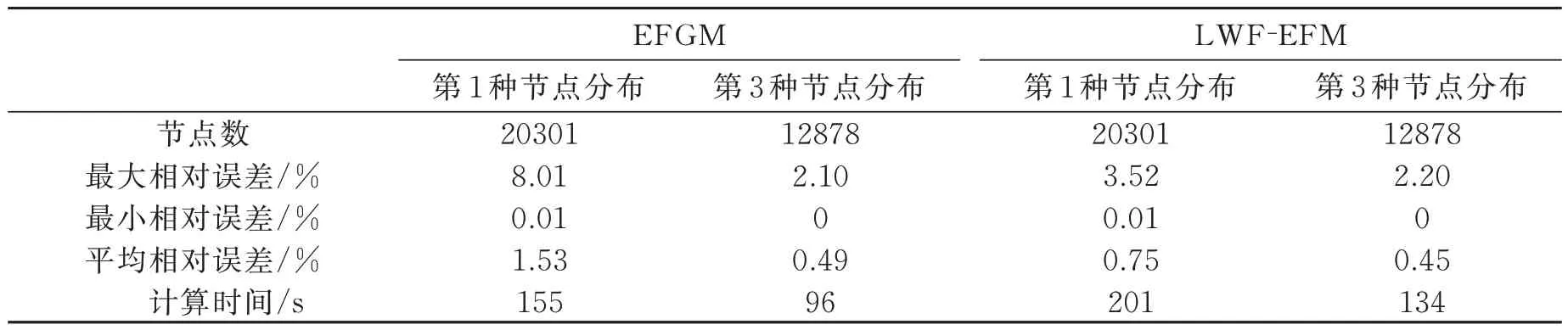
表2 二维模型LWF-EFM 不同节点分布的节点数、模拟相对误差和计算时间

4.3 复杂地电模型

建立图14a 所示水平地形起伏模型，地下空间介质电阻率ρ1=100 Ω·m。计算域Ω覆盖x方向300 m（-150～150 m），垂直方向（z）最大深度为115 m，山脊最高点高度为7.6 m，位于x=-14 m 处，山谷最低处位于x=10 m，高度为3.4 m［51］。

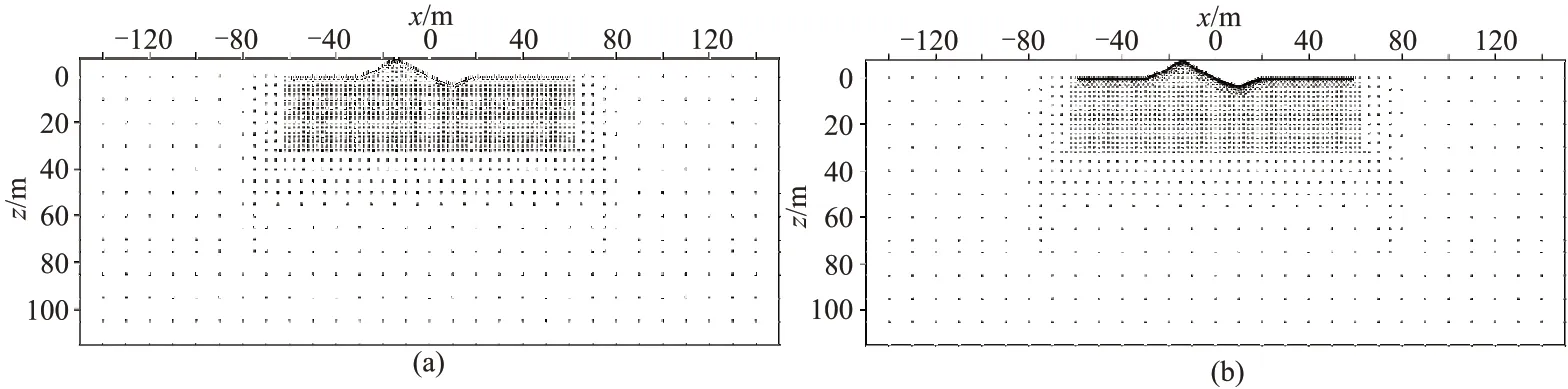
图14 地形起伏模型节点示意图

基于图14a 所示节点分布，采用不规则节点对场源附近的浅层区域和地形起伏区域进行节点加密，在计算域的外围区域使用稀疏节点分布（图14b）。分别采用LWF-EFM、EFGM 和FEM 对模型进行正演，模拟直流电阻率法的视电阻率。采用EFGM 模拟时，在地形起伏区域采用任意四边形背景单元模拟地形。为减小边界影响，采用FEM 模拟时，在上述计算域的基础上进行扩边，扩边后水平方向宽2000 m，垂直方向高1000 m。

图15 为分别采用地形起伏模型未加密节点分布（图14a）和地表加密节点分布（图14b）时，EFGM、FEM 和LWF-EFM 模拟结果。由图可知，无论采用未加密节点还是加密节点，EFGM 和FEM 的计算结果基本一致。其中，EFGM 通过采用任意四边形背景单元，很好地模拟了地形起伏。对比图15c（左）与图15a（左）、图15b（左）可知，在局部区域LWF-EFM与EFGM 和FEM 的模拟结果有较明显的差异，表明在地形起伏区域，若采用较稀疏的节点分布，LWFEFM 对地形起伏模型的模拟精度较低。其主要原因是LWF-EFM 是基于节点局部积分域进行积分，在地形起伏区域节点局部积分域不可避免地会与地形相交，因而不能准确地模拟地形，导致模拟结果出现偏差。在地形起伏区域，LWF-EFM 采用节点局部积分域进行积分，理论上当节点局部积分域与地形相交时，需要将位于地形以外的积分域区域删除。相比于EFGM 和基于非结构化三角形的FEM，LWF-EFM处理复杂地形与积分域的难度和工作量会很大，因此需要提高LWF-EFM 对地形的模拟精度，

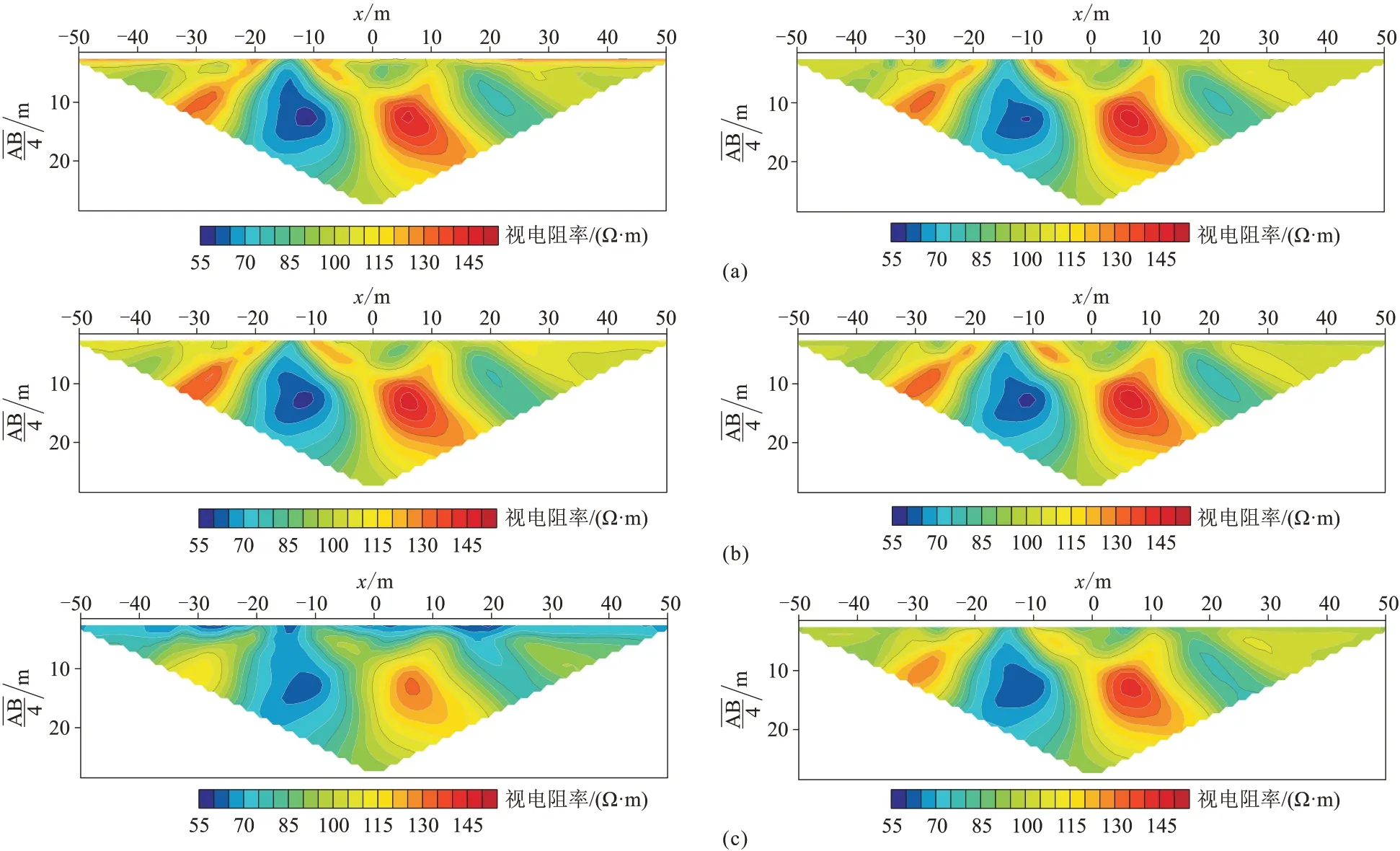
图15 地形起伏模型采用未加密节点（左）和加密节点（右）时不同方法正演视电阻率拟断面

首先，由于LWF-EFM 通常根据节点分布构造节点局部积分域，本文对地表起伏段进行合理的节点加密，使得靠近地形起伏区域的节点局部积分域使用较小尺寸的剖分单元，可更精确地描述地形起伏形态，提高对地形的模拟精度；同时，在地表起伏区域和源附近加密节点，也有利于提高模拟精度。其次，当高斯点位于地形以外时，本文采用对高斯点不做计算的处理策略。虽然这可能出现同一子域内部分高斯点进行了计算而另一部分高斯点不做计算的情况，造成一定的积分误差，但这样处理方法简单方便，同时可保证积分区域尽可能地贴合地形。

图15c（右）为LWF-EFM 经上述两种方法处理后的模拟结果。对比图15c（左）与图15c（右）可知，在地形起伏区域进行加密节点可明显改善LWFEFM 对地形起伏模型的模拟效果。对比图15c（右）与图15a（右）、图15b（右）可知，若采用加密节点，三种算法对地形起伏模型的正演模拟结果基本一致，表明采用上述两种方法可有效提高LWF-EFM 对地形起伏的模拟精度。此外，由于LWF-EFM 采用节点局部积分域积分，相对于EFGM 需要考虑背景单元分布与节点分布相适应的问题［52］，LWF-EFM在节点加密方面更方便，设计任意节点分布具有更高的灵活性和适应性。

为了模拟地下复杂形态异常体，在地形起伏模型基础上加入具有复杂形态的两个近直立异常体（图16中蓝色和红色区域）。其中，红色区域为高阻异常体，位于地形起伏模型山脊顶点的下方，电阻率为ρ2；蓝色区域为低阻异常体，位于地形起伏模型山谷低点的下方，电阻率为ρ3。

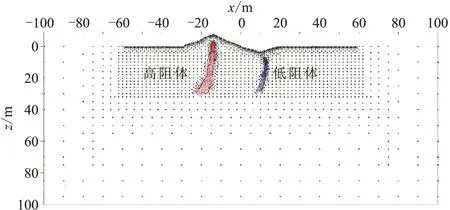
图16 复杂地电模型节点示意图

使用本文方法分别对ρ2=200 Ω·m、ρ3=20 Ω·m和ρ2=5000 Ω·m、ρ3=1 Ω·m 两种情况下的复杂地电模型进行正演模拟，结果如图17 所示。分析图17 可知，山脊地形可以引起明显的低阻异常，山谷地形可以引起明显的高阻异常。对比分析图17a和图17b可知，在山脊和山谷下方分别加入高阻和低阻异常体后，若异常体的电阻率与围岩的电阻率差异不大时，高阻和低阻异常体引起的异常基本被地形引起的异常湮没；随着异常体与围岩之间电阻率差异的增加，异常体引起的异常逐步显现，但未能完全湮没地形的影响。

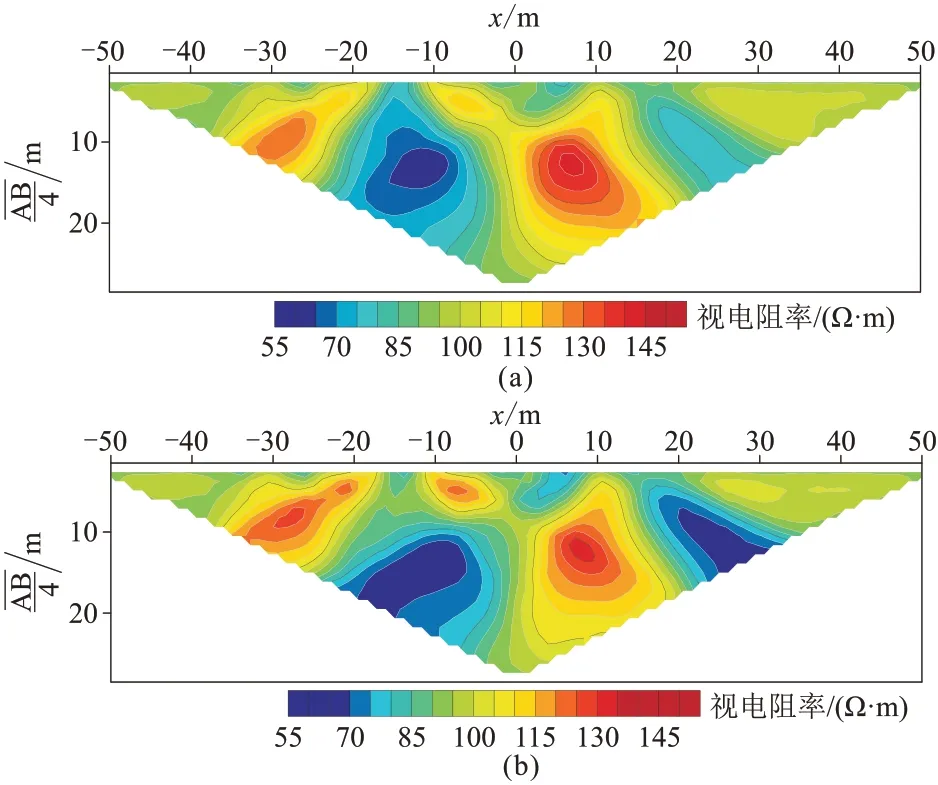
图17 复杂地电模型LWF-EFM 模拟视电阻率拟断面图

因此，对复杂地电模型正演结果综合分析表明，直流电阻率法受地形影响较大，地形之下的异常体（如直立异常体）产生的视电阻率异常很可能被地形引起的异常掩盖。

5 结论

本文提出一种灵活、高精度的直流电阻率无单元局部弱式正演方法。该方法将单位分解积分应用于基于全局弱式积分的直流电阻率EFGM 正演，将全局域积分转化为节点局部积分域积分。对不同地电模型应用三种方法（EFGM，FEM，LWF-EFM）进行数值模拟，结果验证了本文算法应用于直流电阻率正演模拟的正确性和有效性。与EFGM 相比，本文算法无需在全局域内进行背景积分单元剖分；与FEM 相比，本文算法不需要进行基于节点拓扑关系的单元剖分，是一种更灵活性、适应性较强的高精度无单元正演模拟算法。模拟结果表明，由于本文算法采用的不同节点局部积分域之间通常存在很多重合区域，导致实际积分面积比计算域Ω大，计算量也随之增加。地形起伏模型模拟结果分析表明，相比于EFGM 和FEM，本文算法在地形起伏区域节点局部积分域不可避免地会与地形相交，不利于地形起伏模型的精确模拟，因而本文对地形起伏区域进行节点加密，对地形以外的高斯点不做计算，明显提高了地形起伏模型的模拟精度。