基于不完美硬件系统的双智能反射面辅助波束赋形设计*

薛 昊，李 烨

（上海理工大学，上海 200093）

0 引言

近年来，IRS 被提出作为在未来无线网络中实现智能和重构信号传播环境的关键技术[1-2]。IRS 是一个由大量低成本的被动反射元素组成的超表面，通过自适应地调整IRS 的每个元件的反射振幅和相移，电磁波的强度和方向变得高度可控，从而反射信号可以在不同的接收机上有意地增强或减弱。此外，IRS 比传统的有源收发器、中继器消耗的功率少得多，因为它只是反射信号，没有为放大信号注入任何功率[3]。IRS 辅助无线通信作为一种新兴且具有前途的解决方案，可以降低波束赋形过程的硬件成本及能耗成本并获得优异的波束赋形增益。

关于IRS 辅助的无线通信系统已经有了一些研究。文献[4]考虑了一个多输入单输出系统，利用分数规划将多用户和速率最大化问题分解为4 个不相交的块，随后基于非凸块坐标下降的方法设计了低复杂度算法。文献[5]研究了使用IRS 辅助非正交多址系统，采用基于流形优化和逐次凸逼近的方法来设计功率分配矩阵、移相器矩阵和混合波束赋形矩阵。以上关于IRS 的研究主要是基于单IRS 的场景，为了进一步扩大无线通信系统的覆盖范围，以下一些工作对双IRS 辅助通信进行了研究。例如，文献[6]研究了在多用户MIMO 系统中，使用双IRS辅助联合设计两个被动波束赋形矩阵；文献[7]提出了一种双IRS 辅助增强的上行MIMO 系统的相移设计；文献[8]提出了双IRS 辅助，使用流形优化和最小均方误差的方法来求解最大化用户和速率。这些研究结果表明，双IRS 辅助网络在提高频谱效率和扩大无线网络覆盖方面具有巨大的潜力。

然而，以上研究都假设发射机具有完美的硬件条件，没有考虑不完美硬件带来的潜在问题。实际应用中射频组件会遭受不可避免的硬件损伤，包括相位噪声、量化误差和放大噪声等[9]。分析和实验结果均表明，由多余的收发器硬件损伤引起的失真噪声可以建模为加性高斯分布，其方差与信号功率成正比[10]。最近的一些研究分析了不完美硬件对IRS 辅助系统的影响[11-13]，例如：文献[11]中推导出了IRS 辅助系统中断概率的封闭表达式，揭示了硬件缺陷对可实现的频谱效率有显著影响；文献[12]提出了鲁棒波束赋形设计，通过考虑收发器的硬件损伤，使IRS 辅助的单用户多输入单输出系统的接收信噪比最大化。此外，针对单用户多输入单输出系统，文献[13]通过考虑基站端射频硬件损伤和IRS 端的相移噪声，研究了上行信道估计和下行收发器的设计。

综上所述，在基站端具有不完美硬件的MIMO系统中存在失真噪声，这会导致用户接收信号受到失真干扰，系统频谱效率降低。本文研究使用双IRS 辅助进行波束赋形设计，主要工作如下：

（1）由于不完美硬件系统引起的失真噪声和多用户干扰在目标函数中都是非凸函数，因此引入双IRS 辅助通信后，信道数量增加，优化变量高度耦合，目标函数非常复杂。为解决此问题，对复杂的目标函数进行推导，将其转换为凸函数形式。

（2）目标函数中有3 个高度耦合的变量，使用交替优化的方法将原问题解耦为3 个子问题，子问题中使用半正定松弛算法（Semi-Definite Relaxation，SDR）和奇异值分解归一化方法迭代求解最优值。

（3）对该方案进行仿真实验，结果表明在具有不完美硬件MIMO 系统中，与“只有一个IRS”和“无IRS”等方案相比，使用双IRS 辅助通信能够获得更好的系统频谱效率。

1 系统模型

如图1 所示，在双IRS 辅助通信MIMO 系统下行链路中，基站有M根主动天线，部署两个配备了N个反射元素的IRS1 和IRS2，以提升传输性能。该系统模型由基站、IRS1、IRS2 和接收用户4 个部分组成。每个部分之间都有一条单独的通信链路，基站与IRS1 之间的通信链路为G1∈CM×N，基站与IRS2之间的通信链路为G2∈CM×N，IRS1 与IRS2 之间的通信链路为H∈CN×N，IRS1 与用户k之间的通信链路为h1,k∈CN×1，IRS2 与用户k之间的通信链路为h2,k∈CN×1，基站与用户k之间的通信链路为hd,k∈CN×1。

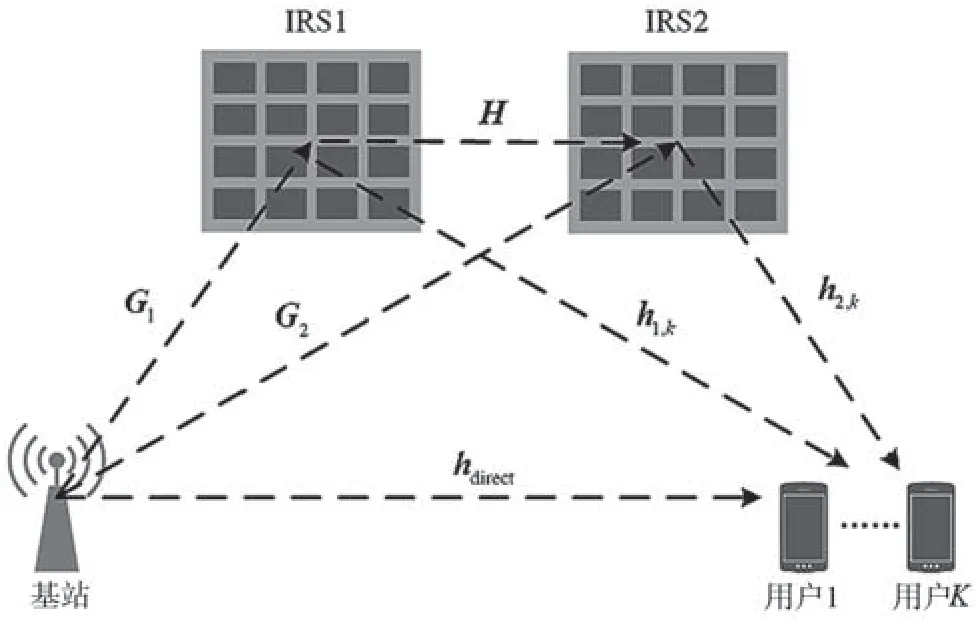
图1 双IRS 系统模型

基站发射信号为：

式中：sk为基站向用户k发送的独立高斯数据符号，满足E[|sk|2]=1；fk∈CM×1为对应的波束赋形向量；mt∈CM×1为独立的高斯发射失真噪声，表示发射端不完美硬件带来的失真信号。每根天线上的失真噪声的功率与其发射信号功率成正比，服从均值为0 的复高斯分布，即：

式中：μt>0 为发射失真噪声功率与发射信号功率的比值。该模型在现有文献中得到了广泛的应用[10-13]，并得到了理论研究和测量的支撑[10]，以精确地模拟实际多天线系统射频链中不完美硬件的联合效应。

从基站发射出的信号经过4 条路径传输到用户k，这4 条路径的表达式为：

式中：Φ1和Φ2分别是IRS1 和IRS2 的相移矩阵，其表达式为：

用户k的接收信号为：

2 问题建模

在求解系统最优频谱效率性能时，通常把用户和速率作为目标函数。令gk=L1+L2+L3+L4，即：

用户k的信干噪比表示为：

用户k的速率可表示为：

式（9）中的各项分别可以转换为：

将式（12）、式（13）、式（14）分别代入式（10），对数函数真数部分进行通分，分子分母同除以(μr+1)，目标函数可转换为：

根据对数函数性质，用户k的速率可写为：

根据对数函数换底公式，式（18）可进一步转换为：

式中：lnAk为凸函数；-lnRk为非凸函数。式（19）整体是非凸函数，无法求解最大值。目标函数是使所有用户的和速率最大化，为求解用户速率的最大值，需要将-lnRk转换成凸函数的形式。

引理[14]：考虑凸函数f(t)=-tx+lnt+1，当t=1/x时，

将-lnRk转换为形如f(t)的形式，令x=Bk，t=tb,k，则：

用户k的速率可表示为：

以最大化系统用户和速率为目标的目标函数可表示为：

式（22）是一个凸函数，可通过迭代方法求解其最大值。在求解过程中，首先将Bk作为已知量求解中间变量tb,k，其次将tb,k作为已知量求解Bk，循环交替迭代直至收敛。

3 算法设计

目标函数中有3 个耦合的变量，分别是基站波束赋形矩阵F和两个IRS 相移矩阵Φ1和Φ2。为求解目标函数的最大值，使用交替优化方法将此问题解耦为3 个子问题，依次优化F，Φ1和Φ2。每优化完一个变量，将其结果作为定值代入下一个子问题中进行求解。

3.1 算法1：基站波束赋形矩阵求解算法

构造向量：

所有信道的总和可以表示为：

将式（26）代入式（16）、式（17），固定v1和v2，优化F，引入辅助变量t=tb,k，根据式（22）的推导，目标函数转换为P(1.1)，则有：

3.2 算法2：IRS1 相移矩阵求解算法

其中，V1满足以下条件：

将式（31）代入式（16）、式（17），固定F和v2，优化V1，引入辅助变量q1,k，根据式（22）的推导，目标函数转换为P(2.1)，即：

算法2 在程序中的实现步骤如下：

3.3 算法3：IRS2 相移矩阵求解算法

将式（38）代入式（16）、式（17），固定F和v1，优化V2，引入辅助变量q2,k，根据式（22）的推导，目标函数转换为P(3.1)：

算法3 在程序中的实现步骤和算法2 相同。

3.4 算法4：交替优化算法

4 实验分析

使用瑞利莱斯信道模型[15]对所提方法进行仿真分析，进行1 000 次蒙特卡洛实验，分别与只有IRS1 或IRS2 辅助、无IRS 辅助这3 种方案进行对比，验证在发射功率、基站天线数量、用户数量、IRS 反射元素数量变化时系统的性能。系统参数配置如表1 所示。为了提升计算精度，以下实验均采用量化方式。

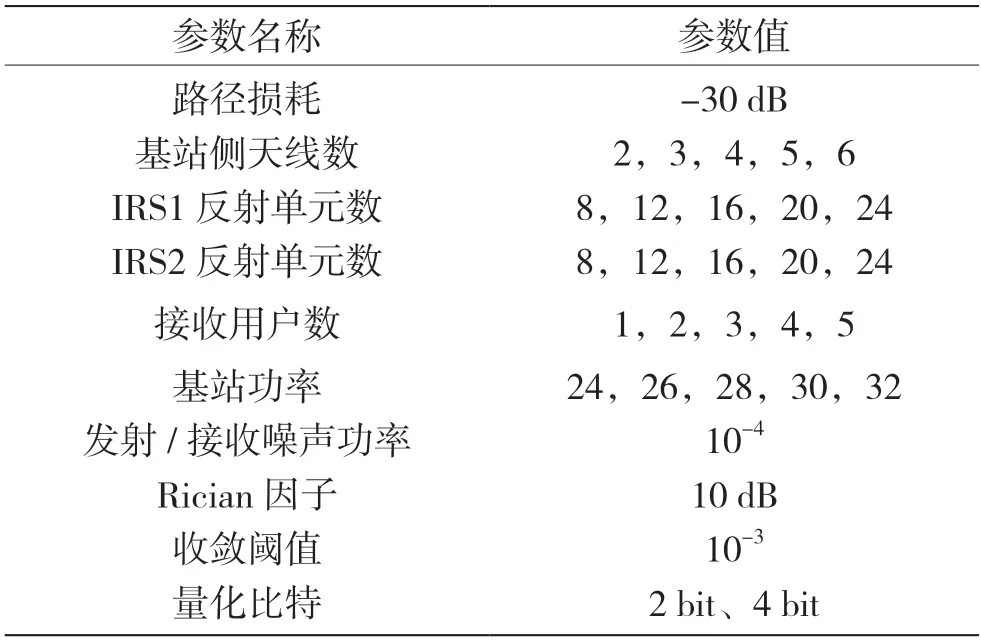
表1 系统参数设置

图2 表示在基站发射天线数为2、用户数为2、IRS1/2 反射元素数量为8 时，系统频谱效率与基站功率的关系，其中基站功率变化范围为24～32 dBm。由图可知，随着基站功率的增大，8 种方案的系统频谱效率都有所上升，无IRS 辅助方案性能最差，双IRS（4 bit）方案性能始终高于其他方案，说明在具有不完美硬件的系统中，通过双IRS 辅助能够获得较好的频谱效率性能。当基站功率为28 dBm时，双IRS（4 bit）与其他方案的频谱效率差值达到最大，随着基站功率的不断提高，不同方案之间的差值逐渐减小；当基站功率为32 dBm 时，双IRS（4 bit）与IRS1（4 bit）性能相同，说明基站功率在一定范围内不断提升能够带来系统频谱效率的提升。

图2 基站功率与系统和速率关系

图3 表示在基站功率为30 dBm，用户数量为2，IRS1/2 反射元素数量为8，发射天线变化范围为2～6 时，系统频谱效率与基站天线数量的关系。由图可知，随着基站天线数量的不断增加，所有方案频谱效率都在提高，无IRS 辅助的方案性能最差，而双IRS 辅助的方案性能最好。当基站天线数量为2 时，双IRS（2 bit）性能低于IRS1（4 bit）方案，随着基站天线数不断增加，双IRS（4 bit）和双IRS（2 bit）方案性能接近，说明量化计算降低了计算误差，提升了系统性能，而发射天线数的增加带来的增益大于量化计算。

图3 基站天线数与系统和速率关系

图4 表示在用户数为2，基站功率为30 dBm，天线数量为2，反射面元素数量变化范围在8～24时，系统频谱效率与IRS 反射元素数量的关系。当反射元素数量为8 时，本文所设计的双IRS 辅助方案所获得的频谱效率低于IRS1 辅助方案，随着反射元素数量的增加，所有方案性能均得到提升，其中使用双IRS 辅助方案提升较为明显。当反射元素数量为24 时，双IRS（2 bit）方案性能比IRS1（4 bit）差，这说明对实验结果进行量化处理能够能到更好的频谱效率性能。本文所提方案更适用于反射元素数量较多的应用场景。

图4 反射元素数量与系统和速率关系

图5 表示基站功率为30 dBm，天线数量为2，IRS1/2 反射元素数量为8，用户数量变化范围1～5时，系统频谱效率与用户数量的关系。通过数据观察，无IRS 辅助的方案的性能是最差的，随着用户数量的增加，使用IRS 辅助的方案增益更大。当用户数量为2，3，4，5 时，双IRS（2 bit）方案性能比IRS1（4 bit）性能差，而双IRS（4 bit）性能优于其余方案，这说明双IRS 与量化比特组合的方案适用于具有不完美硬件MIMO 系统的波束赋形设计。

图5 用户数量与系统和速率关系

5 结语

本文研究了在发射端具有不完美硬件的MIMO系统中，使用双IRS 进行辅助的波束赋形方案。通过推导将复杂的非凸目标函数转换为容易求解的凸函数，并使用交替优化方法将复杂且具有高度耦合变量的目标函数进行解耦，而SDR 算法及奇异值分解归一化方法能够有效地求解基站波束赋形矩阵和两个IRS 相移矩阵。仿真结果表明，在发射端具有不完美硬件的MIMO 系统中，使用双IRS 辅助能够有效地提升系统频谱效率，在IRS 具有大量反射元素的场景下，性能增益明显，优于单IRS 辅助或无IRS 的方案。仿真结果也表明，量化计算也能够提升计算精度，因此在缺乏IRS 硬件的情况下，提高量化精度也能够提升具有硬件损伤的MIMO 系统的频谱效率。