静力荷载作用下埋地HDPE管道受力性能分析

许海洋，韩宁宁，沈德俊，余二林，韩红军，刘鑫

（1．安徽水安建设集团股份有限公司，安徽 合肥 230601；2．合肥工业大学土木与水利工程学院，安徽 合肥 230009）

1 引言

城市地下管线的建设涉及到给排水、燃气、电力、通讯、工业等诸多方面的正常运行，这些都是影响到城市日常运营的关键因素。近年来，随着社会城市化进程的不断加快以及材料科学的不断发展，高密度聚乙烯（HDPE）因其具有抗冲击、抗开裂、耐老化、耐腐蚀、运输方便等一系列优点，使其在管道工程中的应用越来越广泛[1-2]。

在实际工程中，管道系统破坏的后果非常严重，一直是一个棘手的问题，还有可能同时产生其他的次生影响，从而造成巨大的经济损失甚至是伤亡事故，危及社会生产和生活安全[3]。因此，埋地管道系统的安全性和可靠性必须严格满足要求。而静力荷载就是影响HDPE 埋地管道稳定的其中一个重要因素。周敏等[4]对HDPE 柔性涵洞施工及回填时的土拱作用进行了分析，发现随着填筑高度的增大，土拱作用和垂直土压力降低。此外，对HDPE 柔性管进行了地基沉降试验，结果表明HDPE 软管在地基上的垂直变形与高斯曲线相近，覆盖层厚度越大，土拱的作用越显著，对地基的沉陷反应越灵敏，并能抑制变形增大[5]。白子韶[6]对覆土HDPE 管材的变形特征进行了数值模拟，得出了柔性管的变形、应力与柔性管的厚度之间的关系，以及管道附近的应力分布和变化情况。

埋地HDPE 管道在静力荷载作用下的力学响应关系是复杂的，为了明确静力荷载作用下HDPE 管道的受力和变形情况，本文基于ANSYS 建立了埋地HDPE 管道二维有限元模型，分析了土体回填与地表静力作用下HDPE 管的受力变形情况以及管径初始变形、埋土深度等对管道力学响应的影响，研究成果可为实际工程中管道的变形破坏机制提供一定的理论依据。

2 分析实例

分析实例选取为国内某地下截污导流管道，对于具有较长纵向长度的埋地HDPE 管线，其横断面尺寸和形状不随长度而改变，故此次分析可以简化为平面应变问题处理。

平面分析模型可以简化为沥青混凝土面层、回填土、地基和HDPE 管道四个部分，如图1 所示。为了尽可能地减少边界条件对模型分析结果的影响，管道中心距离模型侧边界超过5 倍管道直径，总体尺寸大小为8．0m×7．0m，模型地基深度取2．0m，沥青混凝土面层厚度0．5m，回填土厚度取4．5m。另外，文献[7]中对埋地HDPE管道顶部的最小埋土深度进行了规定，在公路人行道下埋土深度不得小于0．60m，公路车行道下埋土深度不得小于1．00m。综合考虑，本次HDPE 管道模型埋地深度取2．00m、管径取630mm、壁厚取30mm。

图1 地下埋管平面分析模型

3 埋地HDPE管道模型建立

3.1 单元类型

利用ANSYS 有限元软件建立二维有限元模型，本次平面应变问题建模中，管周填土和地基模型采用Plane82 平面单元、埋地HDPE 管道采用Plane183 单元进行模拟。

Plane82 是一个二维8 结点，每一个结点有两个自由度，x 和y 的平动，它可以作为一个平面和一个轴对称的单位。该8 节点单元具有均匀变形的形状函数，能够很好地满足曲面的要求，具有塑性、蠕变、辐射膨胀、应力刚度、大变形、大应变等特性，在四边形、三角形混合网格中，其结果准确率高，能够满足不规则形状要求，且误差小。

Plane183是一种高阶二维8结点实体结构，它的二次位移函数可以很好地满足不规则模式的划分；该单元中的每一个结点都具有x 和y 的平移两个自由度，该单元还具有模拟塑性、蠕变、应力刚度、大变形和大应变的特性，并具有与非压缩弹性体相似的力学性能。

3.2 材料属性

计算模型中主要涉及回填土、地基、HDPE 管道、沥青混凝土面层这四种材料，具体的各材料物理力学参数如表1所示。

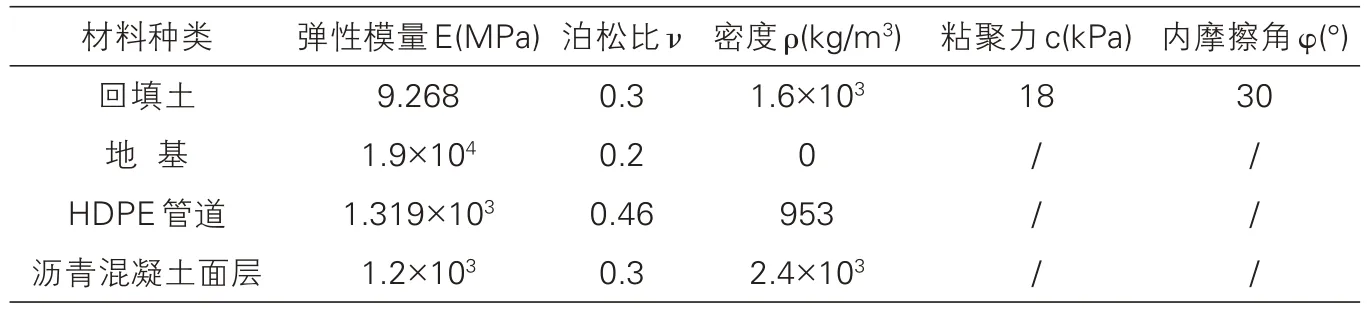
表1 模型材料参数选用表

3.3 模型与约束

本次重点对HDPE 埋地管道的应力和变形进行研究，因此对管道和管道周边的土体进行了一定程度的加密，以保证计算的精确度并提高计算效率。有限元模型及约束条件如图2 所示，模型边界约束设定为地基底部边界为固定边界，两侧土体边界限制x 方向位移，允许y方向移动。

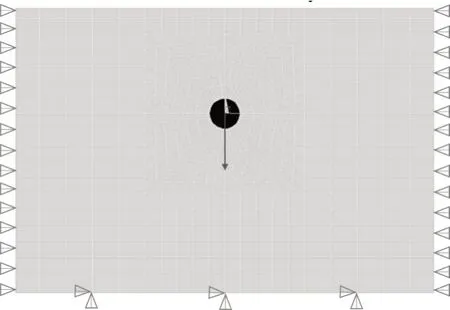
图2 计算模型与约束

4 计算结果与分析

4.1 管道整体受力特点

根据图3 管道在土体自重作用下的竖直方向位移云图可知，在土的自重和应力作用下，管道的竖向变形以管顶部位最大，管底位置最小，说明在土压力作用下，管壁产生水平向外膨胀、竖直方向上受压的椭圆状形变。

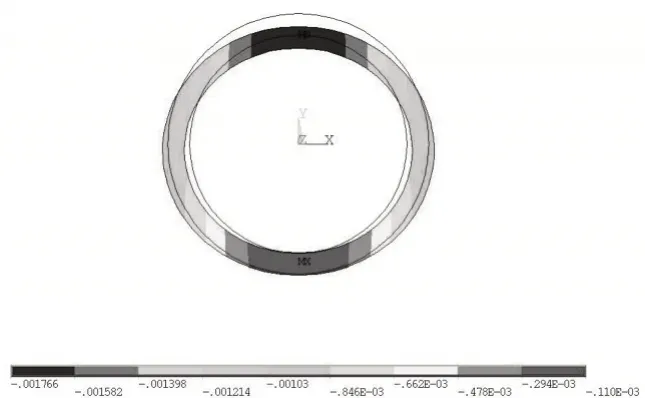
图3 管道竖向位移云图（单位：m）

为了深入了解管道截面的应力分布情况，在管道周身设置关键点，提取等效应力进行分析。关键点的布置如图4 所示。

图4 管周应力关键点布置图

图5 管道内外壁应力分布图给出了管道在土体自重作用下内外壁各关键点处的应力分布情况，从图的变化趋势可以看出，外壁应力分布和内壁应力分布均呈轴对称分布，管道外壁应力在A 点和E 点最大，C 点与G 点次之，D 点与F点最小，即管道在管顶和管底应力均比较大，且管顶应力小于管底应力；在管肩位置外壁应力与内壁应力普遍较小，且外壁应力在与x 轴呈-45°与-135°方向的下半部分管肩位置应力最小；内壁应力趋势与外壁应力恰好相反。该现象表明HDPE 管道在变形时，最大应力出现在管道内壁，内壁最为危险，最有可能先发生破坏，故在设计时应在考虑外部载荷的情形下，充分考虑管道内部压力，避免应力集中。

图5 管道内外壁应力分布图

4.2 管道埋深影响

埋地管道的埋深能直接影响到整个工程的成本、运行的安全性，以及后续的管理维护保养工作。为了防止地下管线受到地面设备和交通工具的损坏，铺设在人行路下面的管线上方的土层厚度一般不低于0．6m，车行道下方地下管线上覆土层一般不小于1．0m，而在铁路下的管道顶部则不小于1．2m。故为探讨管道不同埋深下的受力特征，讨论直径D=630mm，壁厚δ=30mm 的HDPE 管道分别在0．8m、1．0m、1．2m、1．4m、1．6m埋深下的应力、应变变化规律。

管道埋深对管道受力性能的影响模拟，采用两种不同的荷载组合进行对比研究。第一种为管道结构自重与管道所受土压力组成的荷载；第二种为管道结构自重、管道所受土压力以及地面堆积荷载组成的荷载，其中假定地面堆积荷载为静载荷，大小取值为100kN，荷载作用于管道中心正上方。

定义Uh、Uh、D 分别为管道的横向变形量、竖向变形量和管径。图6 管道径向变形对比图给出了土体自重荷载下，管道埋深分别在0．8m、1．0m、1．2m、1．4m 和1．6m 时管道水平方向相对变形Uh/D 与竖直方向相对变形Uv/D 的变化规律。从图中可以得出，管道横向相对变形Uh/D 随深度的增加而增大，而竖向相对变形Uv/D 则随深度的增加而减小，说明管道在土压作用下会出现横向向外膨胀、竖向向内受压的椭圆形变形，并随深度的增加而增大。

图7 和图8 给出了管道埋深分别在0．8m、1．0m、1．2m、1．4m 和1．6m 时管周各关键点的径向应变与环向应变。从图中可以看出，随着管道埋入深度的增大，管道附近的各个关键点处的应变都有一定的变化，即埋入深度越大，对管道的影响就越大。对管周各个部位的应变分布进行分析发现，管周的径向应变基本为正，且一般较小，分布较均匀，说明管道的径向主要是受拉应力；管道的环向应变在管道的两边呈正，而管道肩部、上、下端为负，说明管道的受力集中在管顶、管底附近。

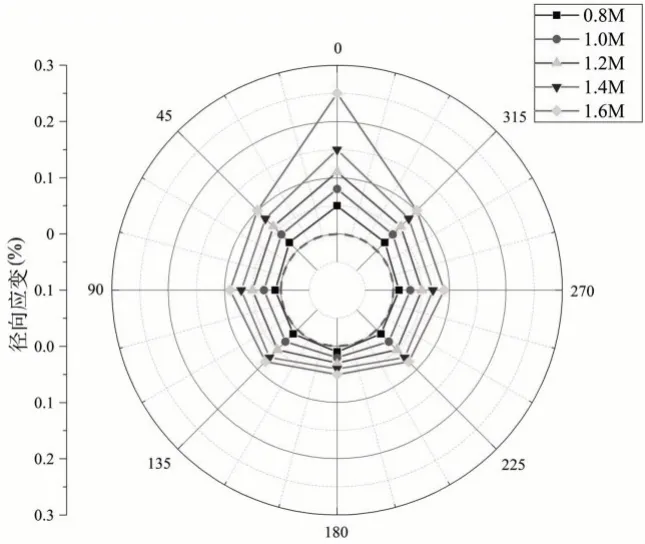
图7 不同埋深下的管周径向应变

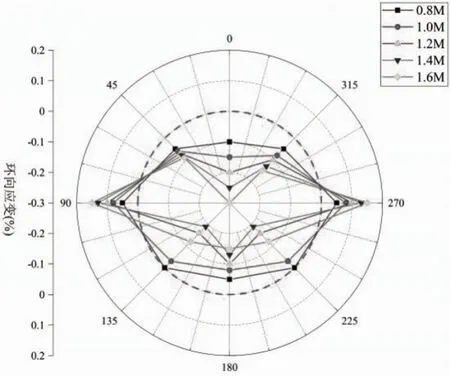
图8 不同埋深下的管周环向应变

图9 与图10 给出了埋地管道分别在土体自重作用与静载作用下管顶应力随埋深的变化情况，由图9 和图10 可以得出，二者总体相比较而言，无论埋深多深，静载作用下的管顶应力明显大于土压力作用下的管顶应力。土体自重作用下，管顶应力大小随着管道埋深的增加近乎呈线性增长关系。对于静载作用下的管顶应力，在一定埋深范围内，管顶应力大小随管道埋深的增加而逐渐减少，埋深1．2m 之前管顶处应力变化程度较大，埋深超过1．2m 之后，管顶应力减小趋势逐渐平缓。即随着埋深的增加，地表静荷载作用于管道的效果越来越弱。

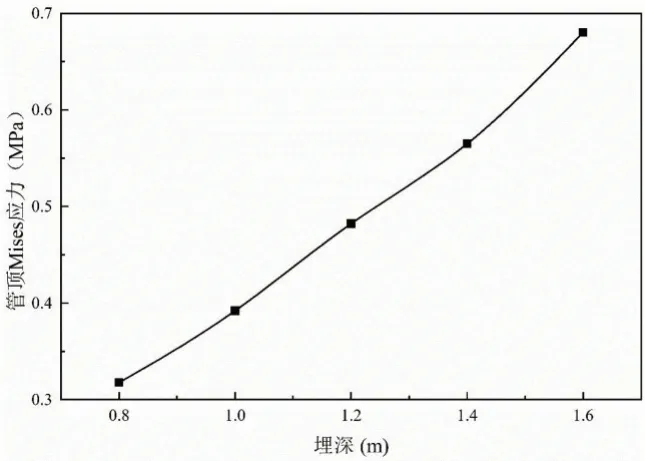
图9 自重工况下管顶应力随埋深变化

图10 静载作用下管顶应力随埋深变化

4.3 管道初始变形影响

HDPE 管材是一种柔性管材，其变形性能优于钢管、钢筋混凝土管材，实际应用中，HDPE 管材由于受外界因素影响，以及输送、堆放过程中的互相挤压而形成的非规则圆截面。为了研究管道初始变形对管道承载能力的影响，假设管道初始圆形为椭圆，用椭圆度Δθ0来表征管道的初始变形，研究管道初始椭圆度为0%、0．2%、0．4%和0．6%，埋深为2．0m，管径为630mm，管壁厚度为30mm时的应力应变关系。

初始椭圆度计算公式为：

式中：Dmax为管道最大外径，Dmax=D+Uh；Dmin为管道最小外径，Dmin=DUV。

图11给出了不同初始椭圆度Δθ0下管周应力的分布情况，由图可以看出，在A、C、E、G 各点，即管顶、管底及管道两侧的应力均随初始椭圆度的增大而变大，其中管道两侧的应力变化最为明显，增长幅度最大；在B、D、F、H 各点，即管肩部位应力基本不发生变化。综合分析可知，管道初始椭圆度对管道周身应力影响很小，在一定埋深范围内，基本不会影响到管道的极限承载能力。

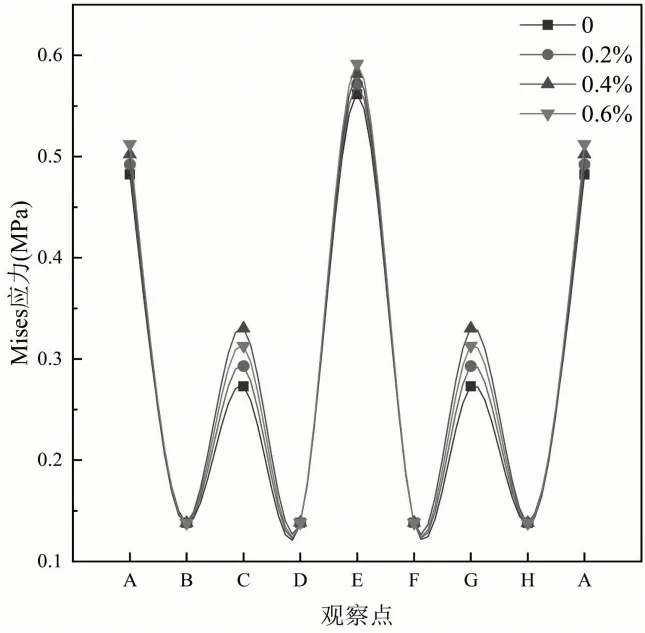
图11 不同椭圆度下管道周身应力分布

为了进一步详细研究不同初始椭圆度下管道的变形特征，沿管周身多增加关键点数量，重新布置关键点位置如图12所示。

图12 管道周身关键点

图13 给出了管道周身各点的径向位移的变化规律，可以看出，上半部分管道管顶与管侧部分径向位移会随着初始椭圆度的增大而逐渐增大，管肩B 与B’处径向位移也会逐渐增大（凹陷），管肩C与C’处径向位移由原本鼓胀状态慢慢凹陷；相比于管道上半部而言，管道下半部分径向位移可以说基本不随初始椭圆度发生变化。

图13 管道周身径向位移

图14 给出了管道周身各点的环向应变随椭圆度的变化规律，可以看出，随着初始椭圆度的逐渐增大，管顶小范围（B-A-B’）与管底附近的环向压应变会随着椭圆度的增加而明显逐渐减小，而管壁B、B’处与管道下半部分(E-F，E’-F’)压应变略显增大。另外，管道左右两侧拉应变明显增大，这是因为管道出现初始变形后，管顶变得更加平缓，而管道两侧变形相对变大。

综上，管道的初始变形越大，在静力荷载作用下埋地管道的变形也就越大，管道抵抗变形的能力会一定程度变弱。

4.4 回填土弹性模量的影响

回填土作为施载者和承载者，其自身的力学性能和变形特性对管道承载能力的影响很大。图15 与图16 给出了土体的弹性模量分别取1MPa、3MPa、6MPa、12MPa、24MPa、48MPa 情况下埋地管道椭圆度的变化规律与管周应力的分布情况。

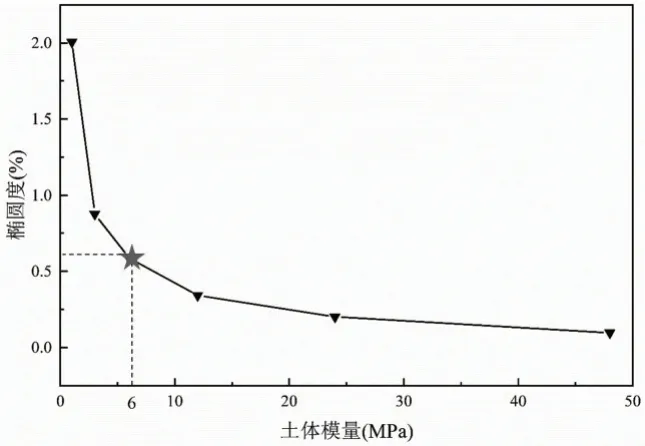
图15 不同土体弹性模量下管道椭圆度

图16 不同土体弹性模量下管周应力分布

从管道的椭圆度来看，土体弹性模量越大，埋地管道的变形越小，土体模量超过6MPa 后椭圆度减小的趋势相对平缓；从管道周身应力分布来看，位于同一埋深的管道，随着周围土体模量增加，管土相对刚度减小，土体的卸荷效应更明显，管道截面变形和应力均减小，说明管道越偏刚性则相对于柔性越容易破坏。

5 结论

①在土压作用下，HDPE 管道变形后的断面形状大致为椭圆形，最大应力出现在管道内壁，内壁最为危险，最有可能先发生破坏，故在设计时应在考虑外部载荷的情形下，充分考虑管道内部压力，避免应力集中。

②HDPE 管道的变形会随埋深的逐渐增大而增大，而地表静荷载作用于管道的效果会随着埋深的增加而越来越弱。因此，在地表面存在静荷载的情况下，适当增大管道埋深对管道整体受力有利，但也意味管道所受到的土压力也随之增大，实践工程中，应该根据地面载荷及回填土性质综合考虑管道的埋深，防止管道发生破坏。

③管道初始变形越大，静力荷载作用下埋地管道的变形也就随之越大，管道抵抗变形的能力也就相对减弱，在实际工程中，应尽量避免管道运输等过程中发生较大的变形，尽可能使管道截面处于最优截面。

④埋地管道的变形量和应力会随回填土弹性模量的增大而减小，即土体模量越大，对管道的影响越微小，选择模量大的回填土对埋地管道整体受力变形有利。因此，在实际工程中，应该重点考虑回填土土体性质、级配情况以及压实度等因素，使管道受力处于最理想的状态。