基于Holt-Winters 乘法模型的小批量物料生产预测研究

秦梦洁，丁学利，王 静，刘金亮

（阜阳职业技术学院公共基础教育学院，安徽 阜阳 236031）

小批量物料生产计划是企业运作管理的重要组成部分，受到了企业和学术界的长期关注。由于无法事前知道物料的实际需求量，根据以往的订单量无法科学、有效地制定生产计划，往往会导致频繁缺货或库存现象，这都对公司经营造成了一定的冲击。若能运用数学方法，建立物料需求量的预测模型，预测值准确度越高，公司投入的成本性资金就越少。小批量物料需求预测的训练数据大多为时序数据。对于时序数据的预测问题，国内外学者也做出了很多研究，但大多是基于SARIMA 或神经网络模型等[1]。这些模型在某些专业领域的精确度比较高，但很难解决所有的时序数据的预测问题。本文采用Holt-Winters 乘法模型对具有周期性变化特征的时序数据进行预测，预测效果较为理想。该模型可为公司制定小批量物料生产计划提供一个简单快速有效的方法。

1 数据来源与分析

本研究的数据来自2022 年全国大学生数学建模竞赛E 题[2]。该题附件1 提供了某公司从2019 年1 月2日到2022 年5 月21 日期间284 种物料的22454 条相关数据，考虑到物料生产的周期性，需将日数据转化为周数据。结合自然年日历，记第一周为2019.01.01-2019.01.06，第二周为2019.01.07-2019.01.13，……。将每周的需求量进行累加，每周的销售单价取平均，共统计出177 周的需求量和销售单价，见表1。

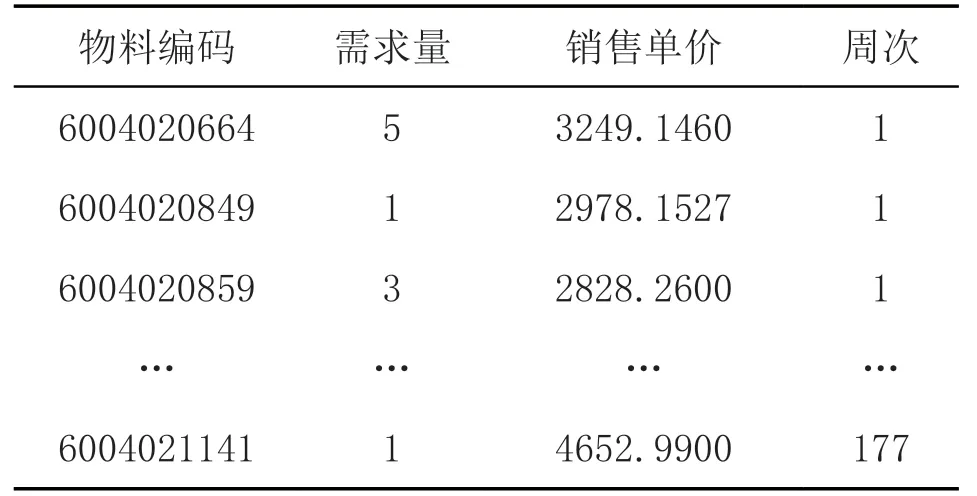
表1 各种物料的周需求量和周销售单价

2 模型建立

2.1 加权Topsis 综合评价模型

加权Topsis 法[3-5]是一种常用于组合综合评价的方法，又称优劣解距离法，即通过计算样本数据与最劣解和最优解的距离进行排序。若样本与最优解的距离最近同时又与最劣解的距离最远，则评价得分高；否则评价得分低。该方法能够充分利用原始样本数据的信息，不仅适用于多评价对象的小样本数据，而且还适用于多指标的大样本数据。具体步骤如下：

1.构造正向化矩阵：把所有指标（包括极小型、中间型、区间型指标）统一转化为极大型指标。记正向化矩阵为：

2.正向化矩阵标准化：标准化后的矩阵记为Z,即：

3.运用信息熵法确定各指标权重。

5.计算百分制综合得分Si：

本研究需要从284 种物料中选取6 种重点关注的物料，以物料的频数、数量、销售单价和趋势作为评价指标，使用加权Topsis 法计算综合得分，得分越高，研究的价值越高。

2.2 Holt-Winters 乘法模型

Holt-Winters 乘法模型[6-11]是一种时间序列分析和预报的模型，该模型是三次指数平滑法的优化版本。考虑到本研究物料需求的时间序列中具有季节性，因此采用Holt-Winters 乘法模型，该模型的运算过程如下：

其中，初值Sp=Yp-Ls（p=1,2,…,s）。Lt、Yt和St分别表示在t时刻的水平值、实际值和季节值。α、β和γ分别表示属于区间[0,1]的水平的平滑系数、趋势的平滑系数和季节的平滑系数。s为季节长度。

2.3 预测模型的评价指标

预测模型的优劣可以用均方根误差（RMSE）和平均绝对误差（MAE）等进行评价，其值越小，说明预测效果越好。计算公式如下：

1.均方根误差：

2.平均绝对误差：

3 结果分析

3.1 加权Topsis 综合评价结果

各种物料需求出现的频数、数量和销售单价分别为每周物料出现的次数、周需求量的总和、周销售单价的均值。物料需求趋势定义为长期趋势、中期趋势、短期趋势。根据同一物料编码出现的周次计算其持续周次，并针对持续周次进行K-均值聚类分析，最终得到各物料编码所对应的趋势，见表2。

表2 K-均值聚类结果

根据聚类分析结果，可得到各物料所对应的趋势类型表（见表3）。

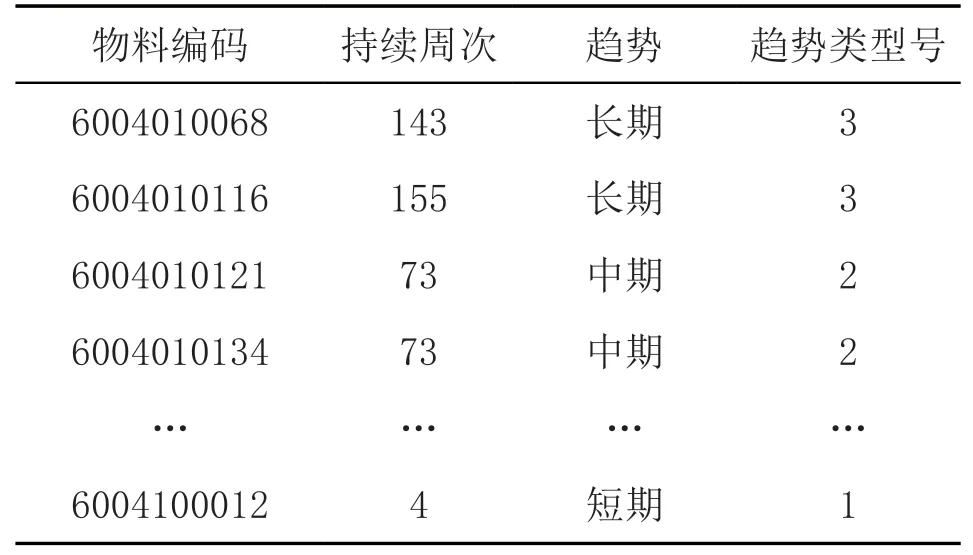
表3 各物料所对应的趋势类型

由表3 可得到物料需求出现的频数、数量、销售单价和趋势这四个评价指标的相关数据，并且这四个指标全为极大型指标（见表4）。

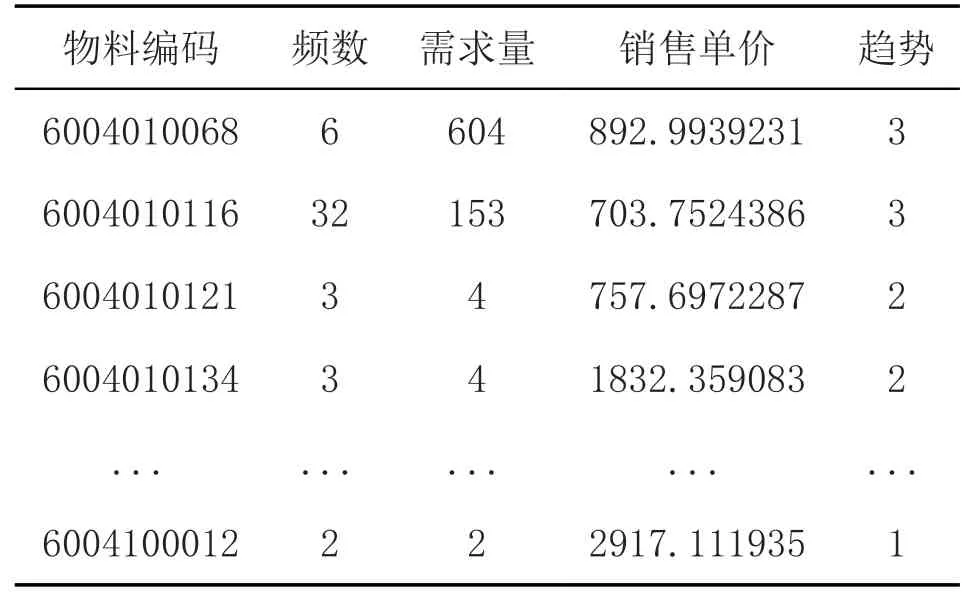
表4 评价指标数据

把表5 的数据代入相关公式进行计算，得到频数、数量、销售单价和趋势这四大指标的权重分别为0.4048、0.4392、0.1209、0.0351。由此可以看出，物料需求量的权重最大，说明它对最终评价值的影响最大。最后代入相关公式计算百分制综合得分。按照综合得分的大小降序排列，即得到各物料百分制评分降序表，由此可选出需要重点关注的6 种物料编码分别为：6004020503、6004010256、6004020918、6004010252、6004021055、6004010174。

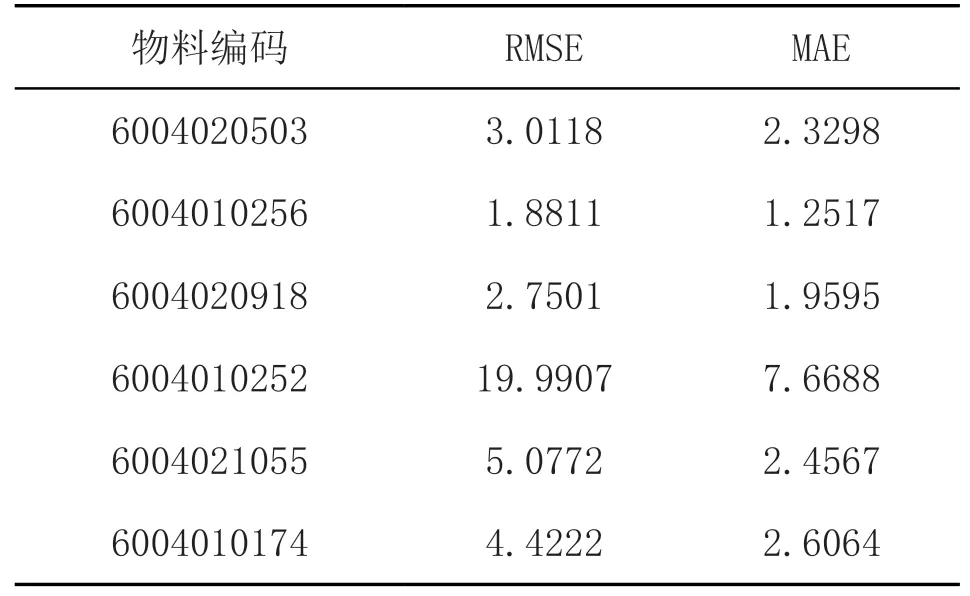
表5 各物料预测总体误差分析

3.2 Holt-Winter 乘法模型预测结果分析

以加权Topsis 综合评价得到的6 种需要重点关注的物料作为研究对象，以第1 周至177 周的物料的需求量作为训练样本，应用Holt-Winters 乘法模型对其进行预测，可得各物料预测总体误差分析表（表5）。

由表5 总体误差分析可以看出，编号为60040102 52 的RMSE 和MAE 都是最大的，说明预测效果较差，通过对比其真实值和预测值数据发现需求量的波动较大（从0 到600 多），且季节性变化不明显，这是使用本模型预测不理想的重要因素之一。而其他5 种物料的预测效果相对较好。

4 结语

针对公司制定小批量物料生产计划的问题，需要找到最优的预测模型，以降低物料的库存量或者缺货量，这样可以减少资金的占用。本文首先用加权Topsis 法从多种物料中选出具有重要研究价值的物料，提高了研究的针对性，再对选出的具有研究价值的物料应用Holt-Winters 乘法模型进行预测和误差分析。研究表明Holt-Winters 乘法模型能较好地对数据进行预测，但对数据波动较大且季节性不明显的数据较难得到合理的预测结果。今后将进一步改进预测模型或使用其它预测模型，以提高对小批量物料生产计划预测的准确度。