考虑吊索拉伸效应的空间索面自锚式悬索桥无量纲连续体动力模型

王晓明，赵建领，孙 远，汪 帆，王 欢，李鹏飞，陶 沛，贺耀北

(1.长安大学公路学院，陕西，西安 710064；2.华中科技大学土木与水利工程学院，湖北，武汉 430074；3.四川省公路规划勘察设计研究院有限公司，四川，成都 610041；4.湖南省交通规划勘察设计院有限公司，湖南，长沙 410008)

作为抗风抗震、车桥耦合振动控制及碰撞冲击防护等动力灾变防控的研究基点，桥梁结构自由振动模型研究持续受到广泛关注[1−3]。这其中，基于有限元方法的离散模型常被用于实时响应的多尺度精细化分析，是结构状态评估与损伤识别的可靠利器[4−5]。然而，有限元方法在模型前期处理过程易忽略未建模动态的关键细节，存在的模型误差使获得的动力响应难以出现一致结果，在有限元模型修正、损伤识别等反演过程中，不可避免面临迭代路径冗长、复杂计算耗时等瓶颈，难以实现结构实时监测与评估[6]。对比而言，基于解析方法的连续体模型不仅能够显著降低模型自由度，同时还可以建立关键参数与动力响应的全局映射关系，进行动力特性的连续参数化分析[7]。因此，建立高精度的连续体动力模型，既能够在较广频率范围内进行动力特性的全局敏感性分析，又能够作为初步设计、模型修正与损伤识别的基准解析模型来提供必要前置数据[8]。

空间索面自锚式悬索桥因其造型轻盈灵动、结构富有张力而常被作为地标性建筑。然而，其缆索的空间耦合性以及子系统间的自平衡特性给连续体模型的建立与求解带来很大困难。首先，不同于常规的平行缆索，空间缆索分处多个平面，主缆与吊索在交互节点处存在力流传递进而改变彼此构形，具有高度空间耦合性。目前，围绕空间索面自锚式悬索桥现有文献多集中于初始平衡状态分析[9]、施工过程中的体系转换[10− 11]等静力研究，其自由振动解析方法研究文献仍较少，HUI 等[12]针对空间索面人行桥建立了6 自由度剖面模型来分析模态参数及非线性特征；XU 等[13−14]基于增量拉格朗日公式与运动学理论建立空间索面悬索桥连续体模型来分析关键参数对动力特性的影响，但上述动力研究仅能分析地锚式悬索桥中跨有限阶次模态，缆索空间耦合性使得能反应全桥模态参数的连续体模型难以建立。

其次，区别于传统地锚式悬索桥，自锚式悬索桥呈现子系统间的内部自平衡特性，其柔性缆-索子系统对塔-梁子系统的压弯变形高度敏感，塔-梁子系统作为缆索的边界约束又进一步触发缆索几何构形和内力的改变，使其非线性问题更为显著，动力特性更为复杂。针对自平衡体系复杂的动力特性，张筱雨等[15]、郭俊等[16]通过引入振动形函数来规避对复杂微分方程的直接求解，进而采用Rayleigh 法得到较为简洁的近似解析解；但其求解精度过度依赖于振动形函数的适配性，仅能获取较为准确的低阶固有频率，无法拓展至高阶次模态参数研究。可见，如何解决上述局限性是关键症结，而围绕地锚式悬索桥的对称性研究可以带来重要启示：经典解析方法融合挠度理论和运动学原理通过推导缆-索-梁振动方程并对其求解来分析模态参数，ABDEL-GHAFFAR[17]研究表明小幅度振动下可将竖向与扭转模态解耦；HAYASHIKAWA等[18]和KIM 等[19]研究表明剪切变形和主梁转动惯量对竖向振动特性影响有限；LUCO 等[20]研究了缆、梁相对刚度对竖向振动的影响；ZHANG 等基于D'Alembert 原理推导了竖向和扭转模态的封闭解[21]，并研究了主缆抗弯刚度对模态的影响[22]。然而，将上述方法直接应用于自平衡体系时，仍将面临复杂微分方程建立与求解难题，目前尚鲜有相关研究，该问题亟待解决。

上述经典解析方法均忽略了吊索弹性刚度对缆-索-梁振动系统的作用，通过假定缆-梁位移一致，使得振动方程较易于求解。此假定的局限性在地锚式悬索桥的相关研究中已有体现：TURMO等[23]以地锚式悬索桥为研究对象，在振动方程推导过程中考虑了吊索的拉伸效应，表明当主梁相对弹性抗弯刚度更大时，吊索弹性刚度对较高阶次模态频率有较大影响；在此基础上，GWON 和CHOI[24]以不同主梁支撑形式的地锚式悬索桥为对象，分析了吊索能否拉伸对模态参数的影响规律，表明吊索拉伸与否会显著影响半漂浮体系悬索桥高阶次反对称模态频率。然而，对于具有缆索空间耦合性和子系统间自平衡性的空间索面自锚式悬索桥，如何在动力连续体模型中考虑吊索弹性变形效应，面临着多体系耦合等因素制约，目前尚未见相关研究报道。

本文将挠度理论推广至振动形态，推导缆-索-梁空间耦合变形方程与相容方程，建立可考虑吊索拉伸效应的空间索面自锚式悬索桥自由振动连续体模型，并将其无量纲化；采用伽辽金方法将模型转化为矩阵形式，求解连续体模型的模态频率及振型；分别利用文献中的平行索面自锚式悬索桥数值算例，以及空间索面自锚式悬索桥有限元算例，验证无量纲连续体模型的精确性与适用性，并对特征参数进行敏感性分析以识别动力特性变化规律。

1 空间索面自锚式悬索桥的无量纲连续体模型

1.1 连续体模型

1.1.1 主缆的空间线形方程

空间索面自锚式悬索桥连续体模型遵循以下假设：① 恒载沿全桥均匀分布，主缆承担全部恒载；② 恒载作用下，主缆线形为抛物线；③ 吊索无质量，主梁不发生纵桥向漂移；④ 由于振动引起的主缆附加水平力远小于初始恒载水平力，因此假设各跨附加水平力相等；⑤ 振动过程中由于吊索可沿轴向拉伸，缆-梁位移不等，但都遵循小位移假定；⑥ 空间索面倾角沿全桥一致，振动中倾角变化量可忽略。

如图1 所示，主缆空间线形投影在竖平面的方程，可依次表示为[23]：

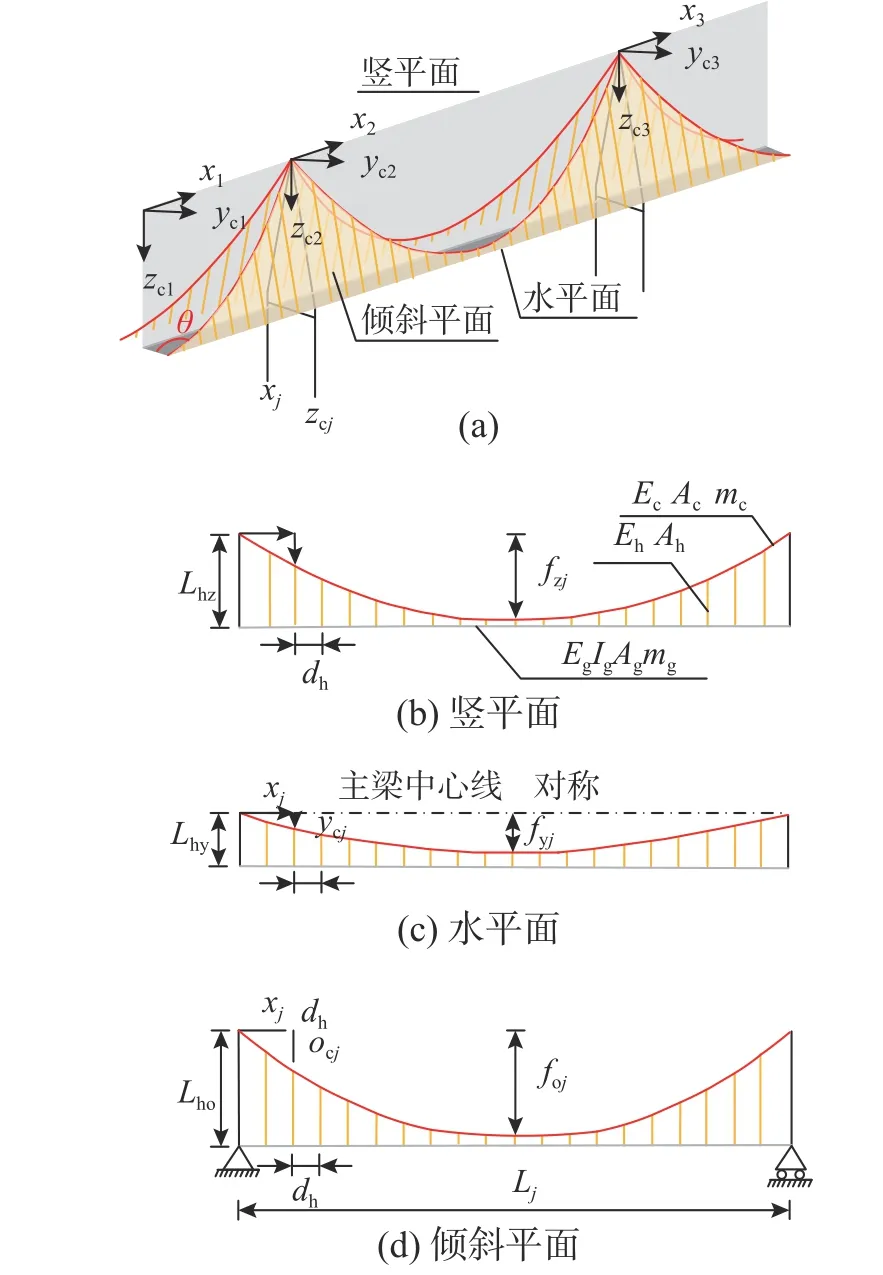
图1 空间索面自锚式悬索桥参数Fig.1 Parameters of a self-anchored suspension bridge with spatial cables

图1 中：mc、mg分别为单位长度主缆、主梁质量；Ec、Ic和Ac分别为主缆弹性模量、惯性矩和面积；Eg、Ig和Ag分别为主梁弹性模量、惯性矩和面积；Eh、Ah分别为吊索弹性模量、面积；Lhz、Lhy分别为主缆IP 点至桥面侧在竖平面、水平面的长度分量；dh为吊杆间距；θ 为空间索面倾角；Lj为各跨跨长；fzj、fyj和foj分别为各跨竖平面、水平面和倾斜平面内的主缆垂度；zcj、ycj和ocj为初始平衡状态下各跨主缆在竖平面、水平面和倾斜平面的坐标。

由假设⑥可得其余两平面主缆线形：

1.1.2 考虑吊索拉伸效应的缆-索-梁空间耦合变形方程

针对其中单跨，Hw为初始平衡态下主缆初始水平力，Hp为振动引起的主缆附加水平力。由假设式(1)、式(2)可得主缆初始平衡态下竖平面、水平面平衡方程为[25]：

式中，hz、hy为吊索竖直、水平分力。在初始平衡态下，hz=mgg/2、hy=mgg/(2tanθ)，则主缆初始水平力：

吊索初始平衡态和振动变形态，如图2 所示，振动过程中竖平面、水平面吊索平衡方程为：

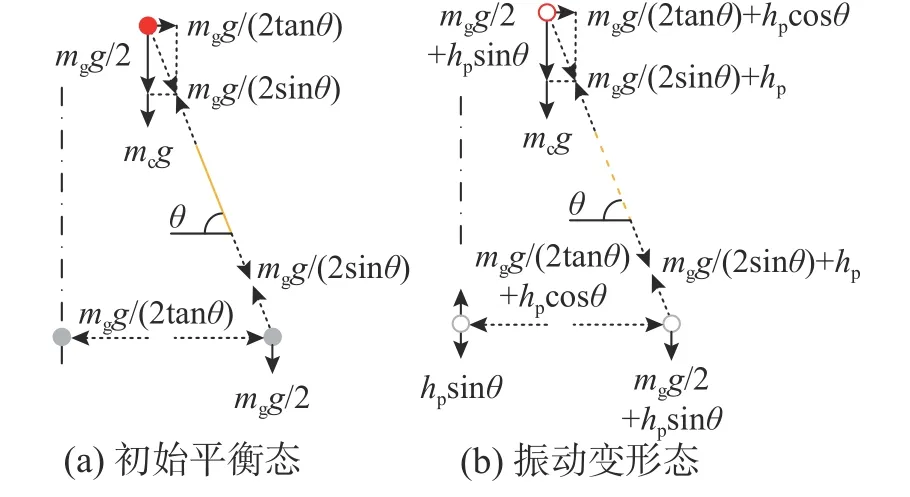
图2 吊索横截面受力图式Fig.2 Load conditions of the hanger in cross-sectional view

式中，hp为振动引起的吊索附加索力，可表示为：

其中，由假设③可得吊索沿主梁方向单位长度的分布弹性轴向刚度kho为：

式中，lho为吊索倾斜长度，lho=Lhz/sinθ−oc。其中，振动引起的吊索伸长量δho，可表示为[26]：

式中：wc、vc为振动引起的主缆竖向、横向位移，wg为振动引起的主梁竖向位移，如图3 所示。

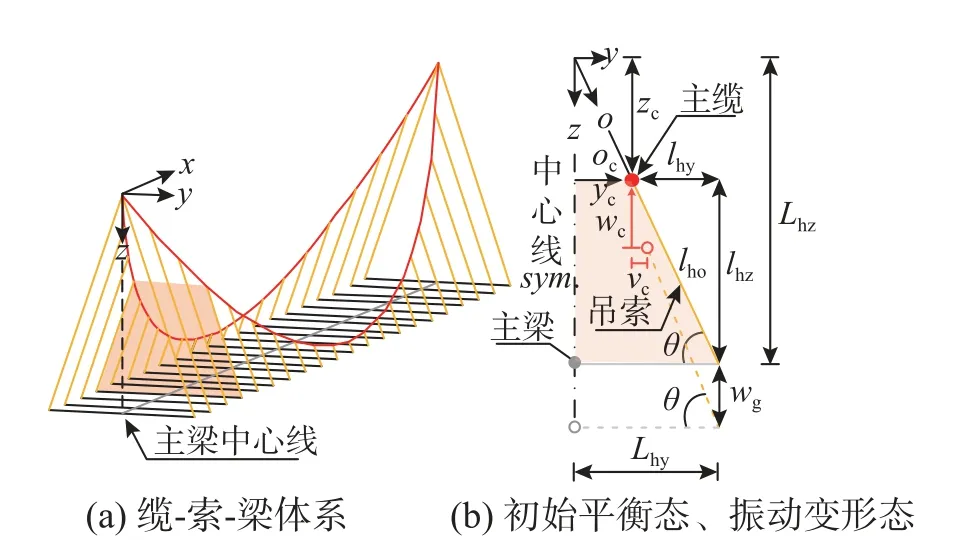
图3 缆-索-梁空间变形图式Fig.3 Spatial deformation conditions of the main cable-hanger-girder

1.1.3 振动形态挠度理论

文献[27]通过建立大位移不完全广义势能泛函，并通过约束变分推导出平行索面自锚式悬索桥竖向振动微分方程，研究表明，忽略主梁剪切应变能，竖向可与纵横向及扭转等模态解耦。据此，本文基于挠度理论并将其拓展至振动形态，主缆振动微分方程可表示为[28]：

主梁振动微分方程可表示为[28]：

由假设式④，Hw+Hp≈Hw；将式(6)～式(8)依次代入式(9)～式(10)化简，重排并拓展至多跨，得到缆-索-梁体系空间耦合振动微分方程组：

式中，方程未知量为主缆竖向位移wcj、主缆横向位移vcj、主梁竖向位移wgj和主缆附加水平力Hp。

1.1.4 考虑自平衡性的相容方程

变形协调作为求解耦合振动微分方程的补充条件[29]，依据自锚式悬索桥缆-索-梁体系受载变形下主缆伸长水平分量与主梁压缩量一致的条件，空间缆-梁变形相容方程可表示为：

将式(12)化简，振动引起的主缆附加水平力可表示为：

式中：

1.2 无量纲化

为更好识别动力特性的控制参数，将式(11)无量纲处理[23]，基本变量无量纲变换可表示为：

将式(14)代入式(11)，得无量纲振动微分方程组：

式中的无量纲参数分别为：

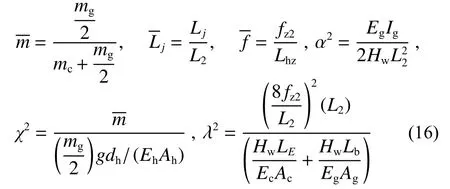
每跨吊索相应的无量纲长度为：

式(15)表明，缆-索-梁体系竖向自由振动特性由式(16)中6 个无量纲特征参数和空间索面倾角共同控制。式中：为主梁相对质量；为边跨相对长度；为主缆相对垂度；λ2为Irvine 刚度系数[30]，表征主缆几何与弹性刚度的关系，即主缆相对弹性轴向刚度；α2为Steinman 刚度系数[31]，是主梁弹性抗弯刚度与主缆重力刚度的比值，即主梁相对弹性抗弯刚度；χ2反映主梁相对质量与吊索恒载应变的关系，即吊索相对弹性轴向刚度[23]。

2 伽辽金求解方法

2.1 缆梁的边界与形函数

主梁为3 跨连续梁，有12 个边界条件，即各支点处竖向位移为0，跨内支点两端转角及弯矩相等，以及边支点弯矩为0：

主缆和主梁的无量纲位移设定为：

式中：N为形函数阶次；为待定系数；是满足式(18)几何和力学边界的主缆振动形函数，可表示为：

2.2 求解流程

建立求解流程如图4 所示，其中各公式推导过程如下。

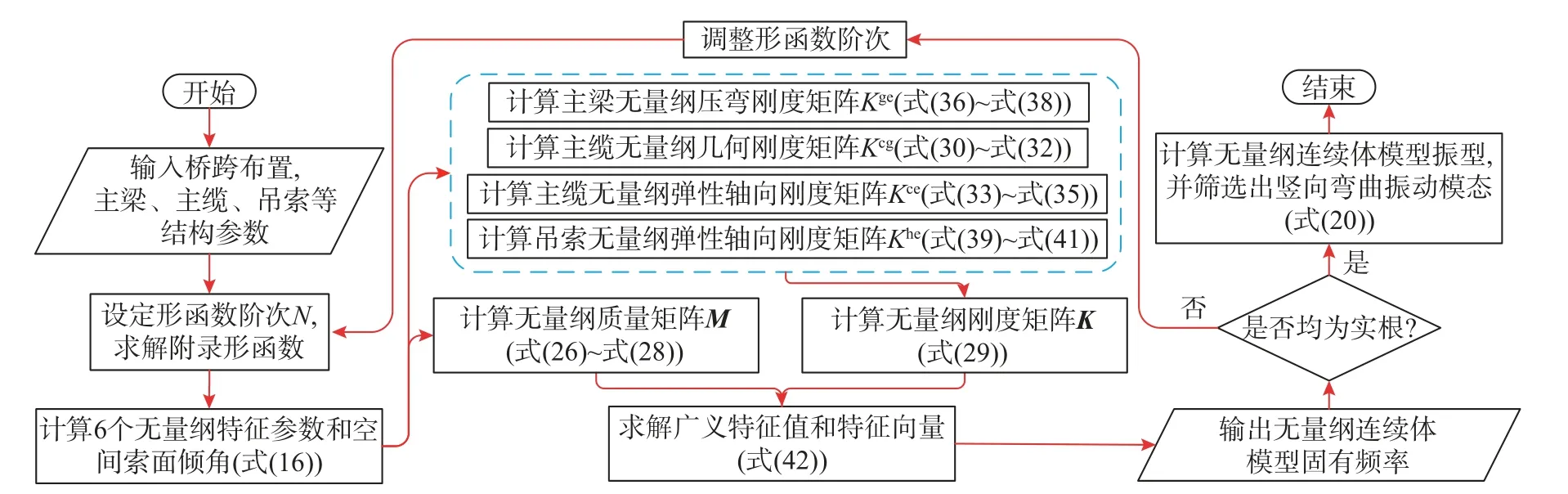
图4 无量纲连续体模型求解流程Fig.4 Solution procedure of the dimensionless continuum model

将式(20)代入式(15)后乘主缆、主梁相应形函数并积分，可到7N 个方程和7N 个未知数(cj1,cj2, …,cjN、g1, g2, …, gN 和rj1, rj2, …, rjN)，格式如下：

将式(22)化简并重排成矩阵形式，可表示为：

式中：

其中：

式(23)中无量纲质量矩阵M7N×7N为对角矩阵，可表示为：

式中：

其中：

式(23)中无量纲刚度矩阵K7N×7N可表示为：

[Kcg]7N×7N主缆无量纲几何刚度矩阵 为对角矩阵，可表示为：

式中：

其中：

式中：

其中：

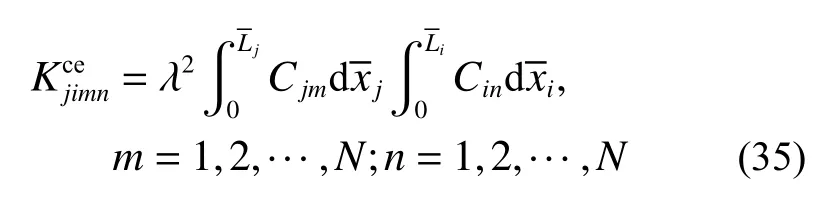
可表示为：

式中：

其中：

式中：

其中：

连续体模型对应的振型可通过式(20)获得，连续体模型固有频率为：

3 算例分析

将本文提出的无量纲连续体模型编制成程序，利用现有数值算例和有限元模型验证连续体模型的普适性与准确性。程序运行环境为：MATLAB R2016a，处理器Intel(R) Core(TM) i7-6700HQ CPU@ 2.60 GHz、内存8 GB。

3.1 文献算例验证

本算例校验不同类型索面下连续体模型的普适性。采用文献[27]中平行索面混凝土自锚式悬索桥作为算例，结构参数详见文献中的表1“构件材料特性和截面特性”。

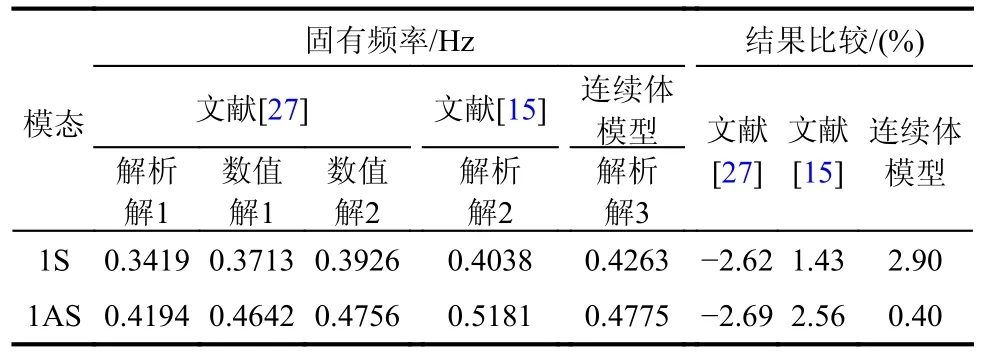
表1 文献与连续体模型固有频率结果对比Table 1 Comparison of natural frequencies between reference and the continuum model

连续体模型中将空间倾角设定为θ=90°，使其退化为平行索面连续体模型，形函数阶次设定为N=10，求解本算例的固有频率及振型，程序运行共耗时25.24 s。固有频率结果对比见表1，其中数值解1 为大连理工大学专用程序DDJ-W 计算结果，数值解2 为ANSYS 计算结果；解析解1 为文献[27]利用大位移不完全广义势能泛函推导出的经典解析结果，解析解2 为文献[15]利用Rayleigh法推导出的计入主塔刚度的近似解析结果，解析解3 为本文考虑吊索拉伸效应的连续体模型给出的经典解析结果。以数值解均值为参考对比三类解析解准确性，连续体模型固有频率与文献结果基本吻合，保证了连续体模型在退化为平行索面时依然具有普适性；连续体模型计算的1 阶对称、反对称振型示于图5。

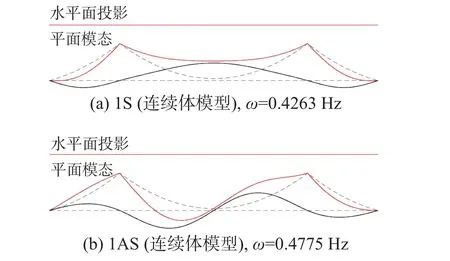
图5 平行索面自锚式悬索桥算例振型Fig.5 Example of a self-anchored suspension bridge with parallel cables mode shapes

3.2 有限元模型验证

本算例校验空间索面连续体模型的准确性。采用MIDAS CIVIL 建立有限元模型进行特征值分析，如图6 所示，桥塔、主梁均采用梁单元模拟，主缆、吊索均采用索单元模拟；吊索-主梁刚性连接，主缆-梁端刚性连接且主梁全桥连续，桥塔塔底固结，结构参数见表2。

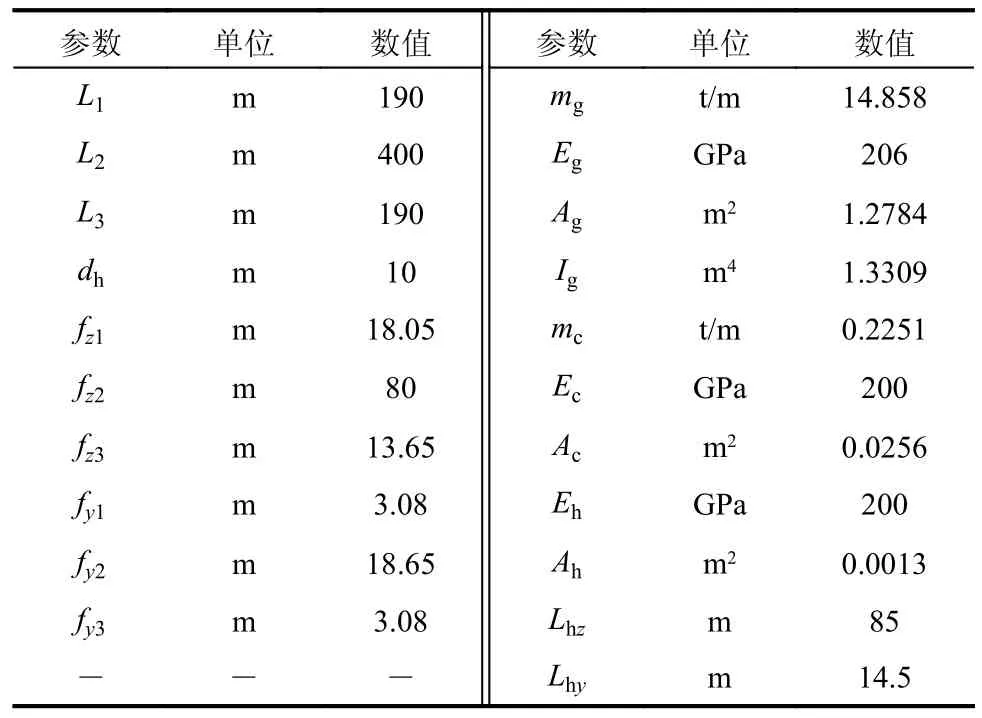
表2 空间索面自锚式悬索桥算例参数Table 2 Example parameters of a self-anchored suspension bridge with spatial cables

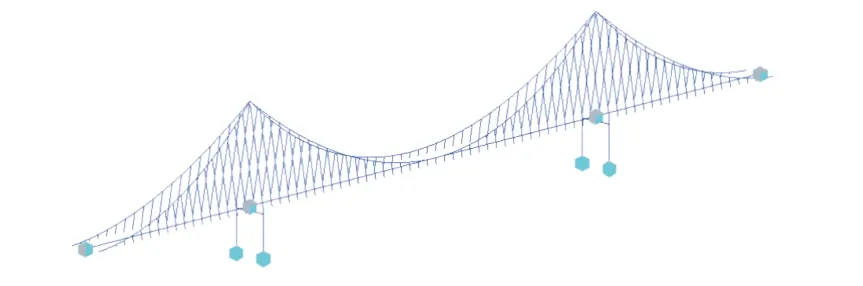
图6 空间索面自锚式悬索桥有限元模型Fig.6 Finite element model of a self-anchored suspension bridge with spatial cables

为便于后续特征参数敏感性分析时验证吊索相对轴向弹性轴向刚度的贡献，按照是否考虑吊索拉伸效应，连续体模型分为2 类：CM-Ext 为考虑吊索拉伸效应的连续体模型，χ2为实际参数计算值；反之，CM-InExt 则不考虑吊索拉伸效应，认为吊索刚度足够大而无法变形，设定χ2=1×106。

连续体模型形函数阶次设定为N=24，求解固有频率及振型，程序运行共耗时90.49 s。前8 阶对称与反对称模态的固有频率，与有限元模型固有频率结果对比见表3，1 阶反对称模态固有频率误差为−6.47%，2 阶反对称模态固有频率误差为−7.89%，其余各阶次模态固有频率误差均在±6%以下，连续体模型与有限元模型结果基本吻合，用于动力特性的连续参数化分析是可靠、准确的；限于篇幅，仅展示前3 阶对称、反对称振型，如图7、图8 所示。

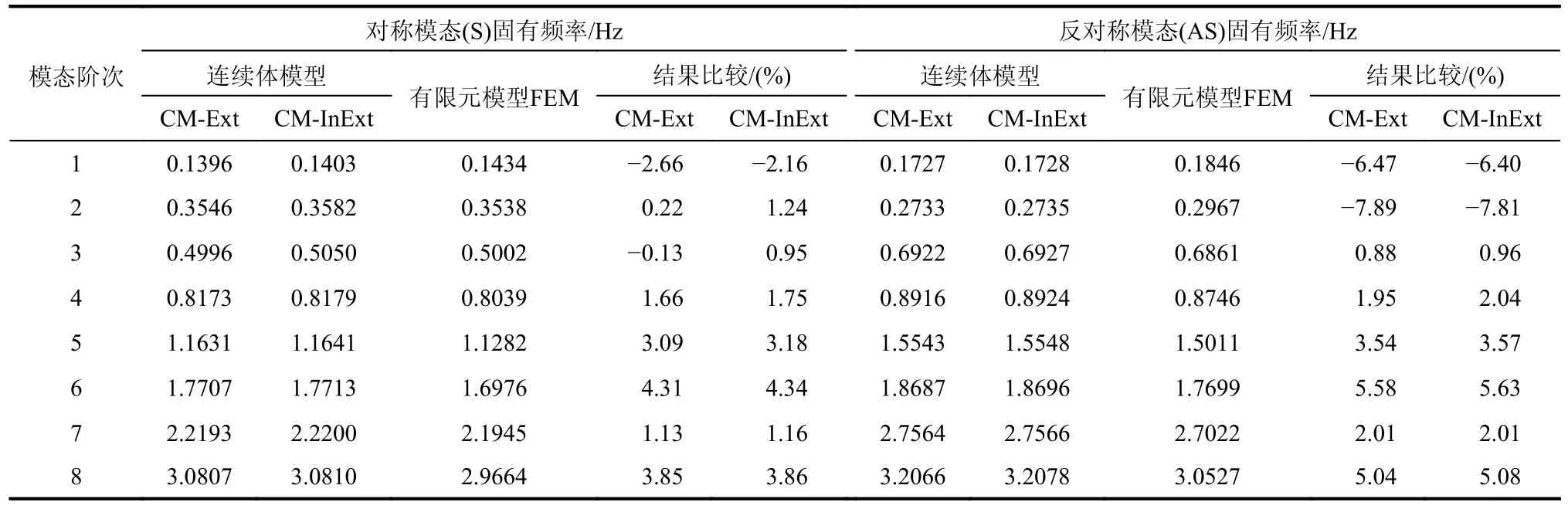
表3 连续体模型与有限元模型固有频率结果对比Table 3 Comparison of natural frequency between the continuum model and finite element model

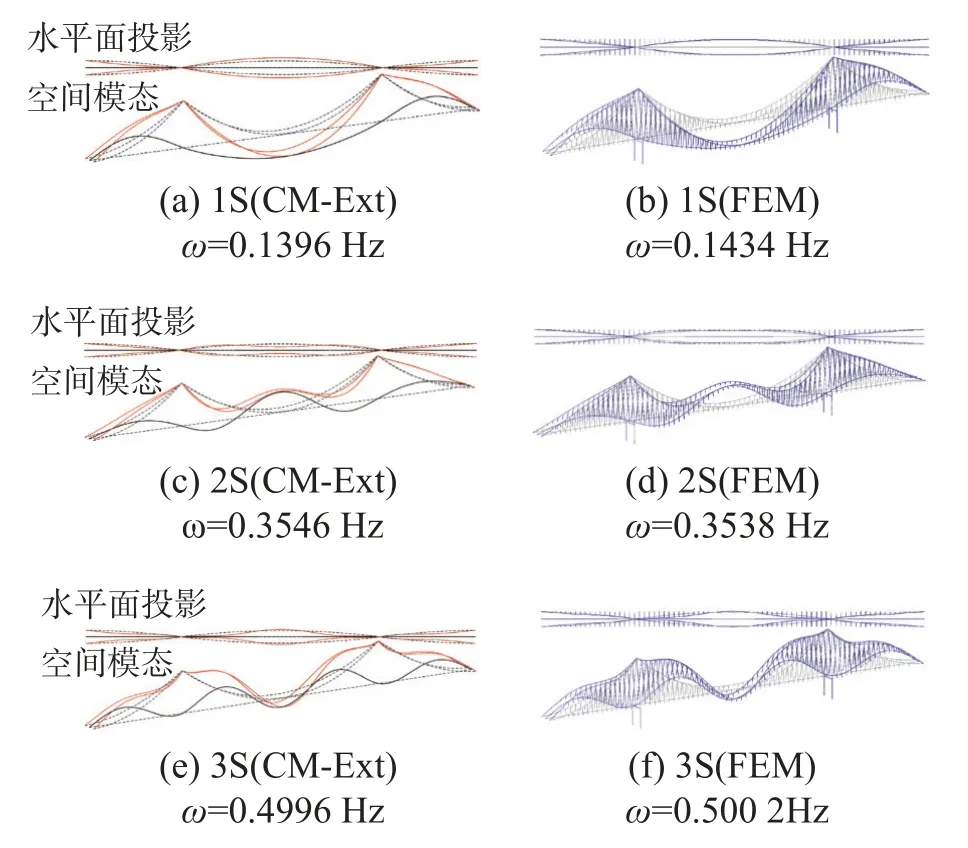
图7 连续体模型与有限元模型对称振型对比Fig.7 Comparison of symmetric mode shapes between the continuum model and finite element model

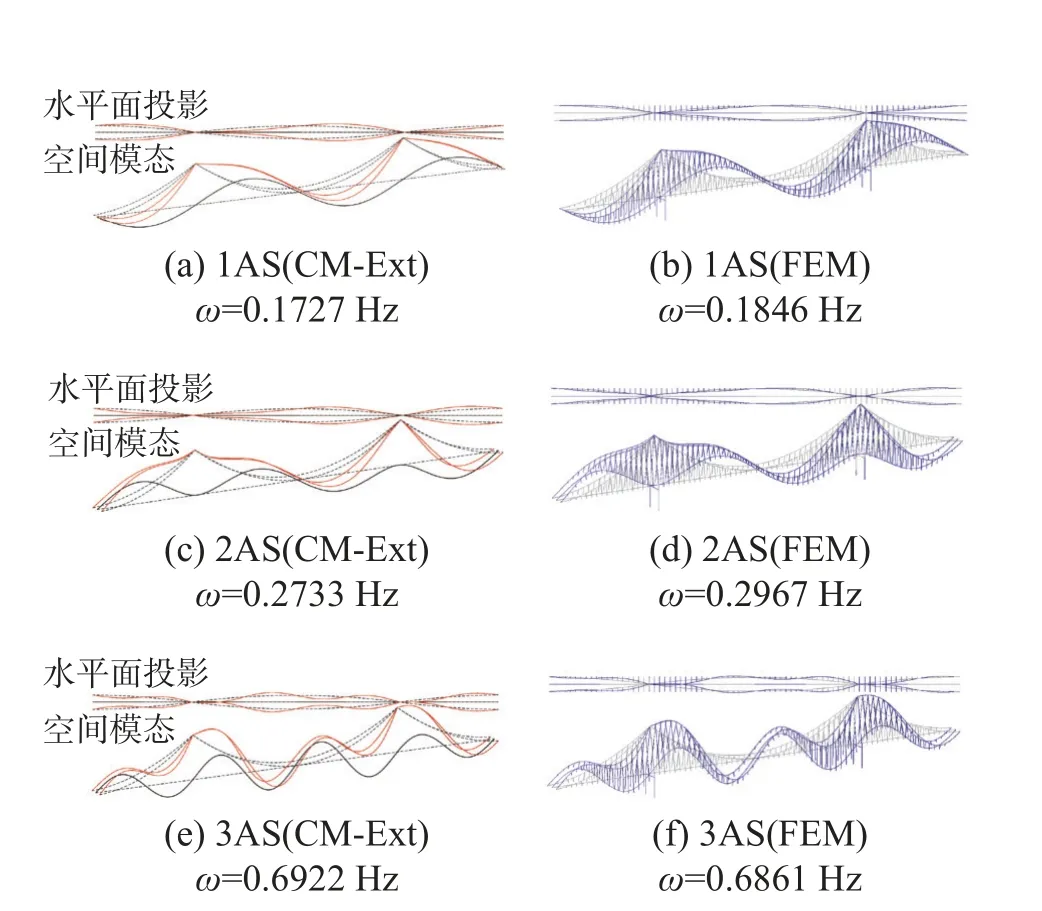
图8 连续体模型与有限元模型反对称振型对比Fig.8 Comparison of antisymmetric mode shapes between the continuum model and finite element model

3.3 特征参数敏感性分析

在研究相对刚度特征参数和空间索面倾角对动力特性的影响时，仅改变既定分析参数，保证其他参数维持不变。分别将主梁相对弹性抗弯刚度设定为 α2/5、α2、5 α2；主缆相对弹性轴向刚度设定为λ2/2、λ2、2λ2；空间索面倾角设定为60°、70°、80°、90°。除此之外，将同时采用CM-Ext与CM-InExt 分别进行动力计算，来分析吊索相对弹性轴向刚度的贡献。

3.3.1 空间索面倾角

图9 展示了空间索面倾角对固有频率的影响。总体而言，空间索面倾角对各阶次模态频率的影响甚为微弱，仅对低阶次(1 阶～3 阶)模态影响稍强，θ从60°增至90°过程中，如图9(a)所示，1S 频率增长分别为3.76%、2.22%和0.73%；如图9(b)所示，1AS 频率增长分别为3.74%、2.28%和0.76%，变化幅度逐渐放缓。高阶次(4 阶～8 阶)模态频率增长均低于0.55%，基本不受索面倾角影响。值得注意的是，改变空间索面倾角的同时，关于主缆的积分项LE也会同步变动，进而导致主缆相对弹性轴向刚度 λ2变更，但其在悬索桥面内的分量仍保持近似一致，这也是模态频率基本不受空间索面倾角影响的原因所在。

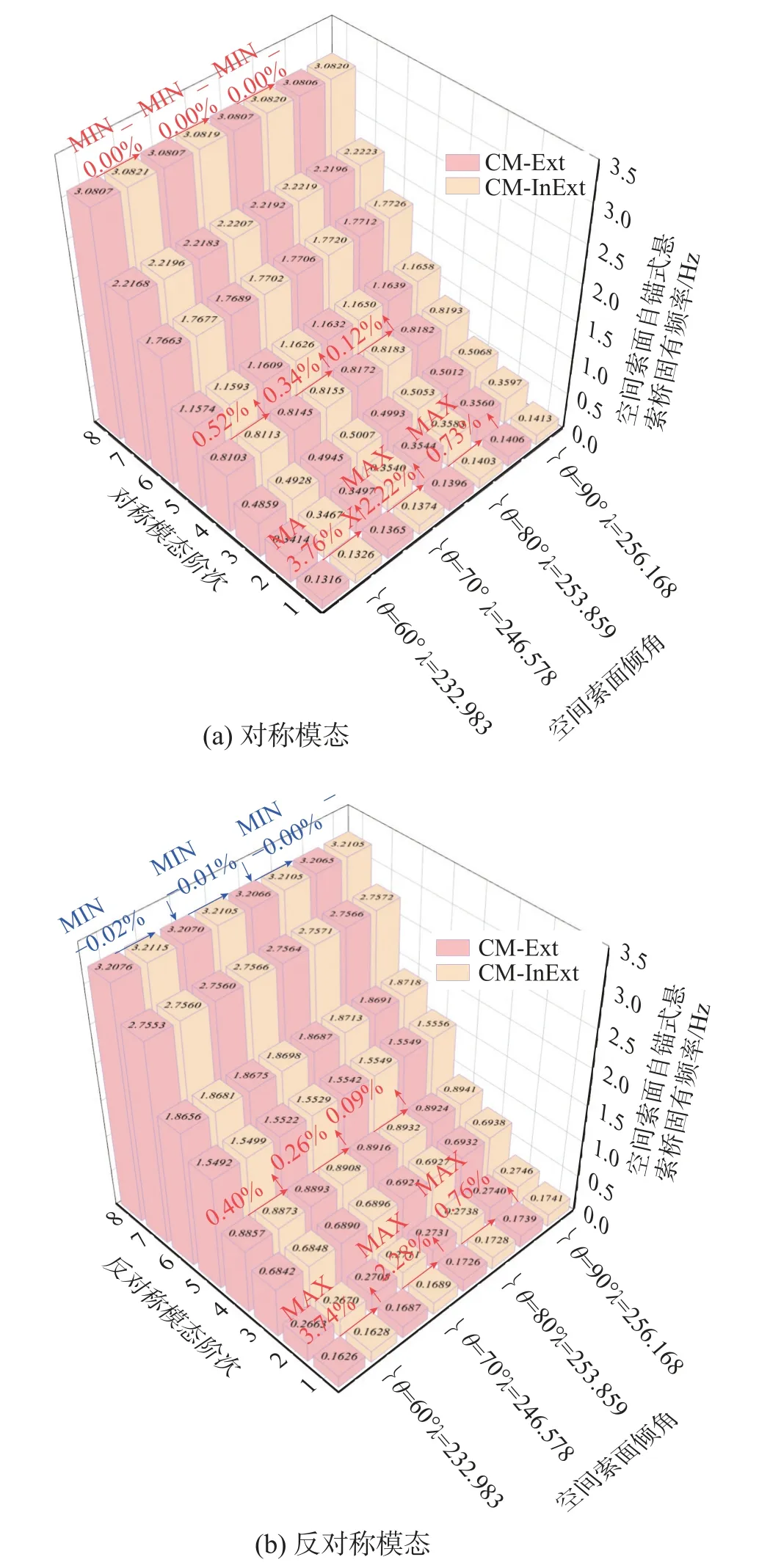
图9 空间索面倾角变化对固有频率的影响Fig.9 Influence of horizontal angle of the inclined hanger plane on natural frequencies

3.3.2 主梁相对弹性抗弯刚度

图10 给出了主梁相对弹性抗弯刚度对固有频率的影响。总体而言，α2增大将显著提升结构整体刚度，使得各阶次频率均随着 α2而增长。图10(a)中，较之高阶次(4 阶～8 阶) 对称模态而言，低阶次 (1 阶～3 阶)对称模态频率增幅较为缓和，其中，3S 频率自 α2/5 增大到 α2时仅增大38.51%，2S 频率自 α2变至5 α2时仅增大64.82%；而高阶次对称模态，各阶次增幅均高于110%，其中，8S 频率自 α2/5 增大到 α2时提升124.85%。如图10(b)所示，与之不同的是，反对称模态频率随着 α2增大均普遍得到显著提升，其各阶次频率增幅均高于115%，且低阶次频率较高阶次增幅稍大。

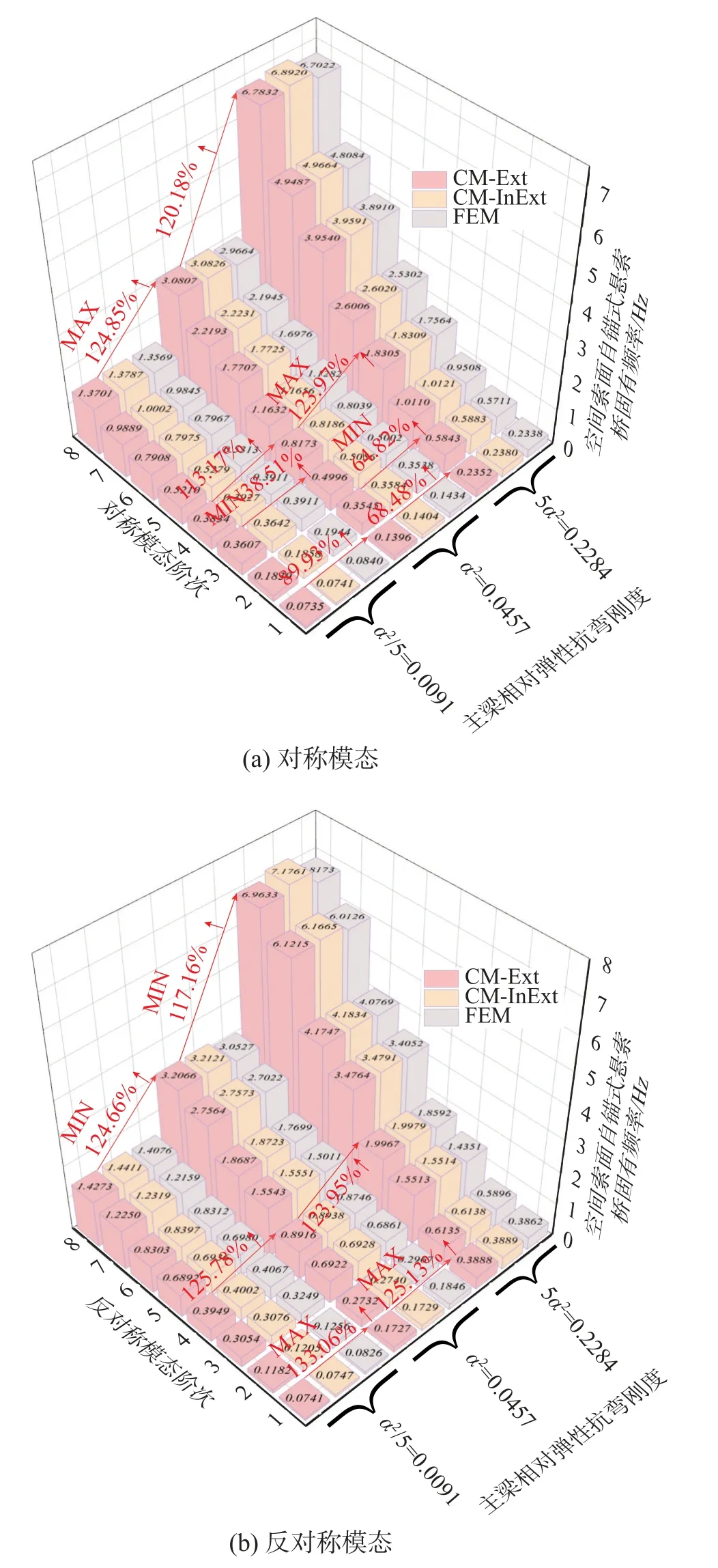
图10 主梁相对弹性抗弯刚度对固有频率的影响Fig.10 Influence of relative elastic bending stiffness of the main girder on natural frequencies

除此之外，当自 α2/5 增大到 α2时，先后出现的前6 阶模态自“1S-1AS-2AS-2S-3AS-3S”变动至“1S-1AS-2AS-2S-3S-3AS”，其中的3AS、3S发生交叉，分别自0.3054 Hz、0.3607 Hz 迁移至0.6922 Hz、0.4996 Hz；后随着 α2增大到5 α2时，先后出现的前6 阶模态自“1S-1AS-2AS-2S-3S-3AS”变动至“1S-1AS-2S-2AS-3S-3AS”，其中的2AS、2S 模态发生交叉(cross-over)，分别自0.2732 Hz、0.3545 Hz 迁移至0.6135 Hz、0.5843 Hz，在结构抗风抗震等动力设计过程中尤其应注意由主梁相对弹性抗弯刚度变化引起的模态交叉现象。

3.3.3 主缆相对弹性轴向刚度

图11 反映了主缆相对弹性轴向刚度对固有频率的影响。与2不同，λ2对各阶次模态频率影响有限，对于提升结构整体刚度的效果稍弱。图11(a)中，λ2对于低阶次(1 阶～3 阶)对称模态影响较为明显，其中，2S 频率自λ2/2 变至λ2时提升15.51%，3S 频 率 自λ2变 至2λ2时 增 大17.99%；高 阶 次(4 阶～8 阶)模态增长率均低于0.2%，基本不受λ2影响。图11(b)中，各阶次反对称模态频率增长均为0，与λ2无关，原因在于在反对称模态下式15 第 1、3 分 式 中 与 λ2相 关 联 的 积 分 项结果为0，这反映了反对称模态下主缆并不能提供相对弹性轴向刚度。

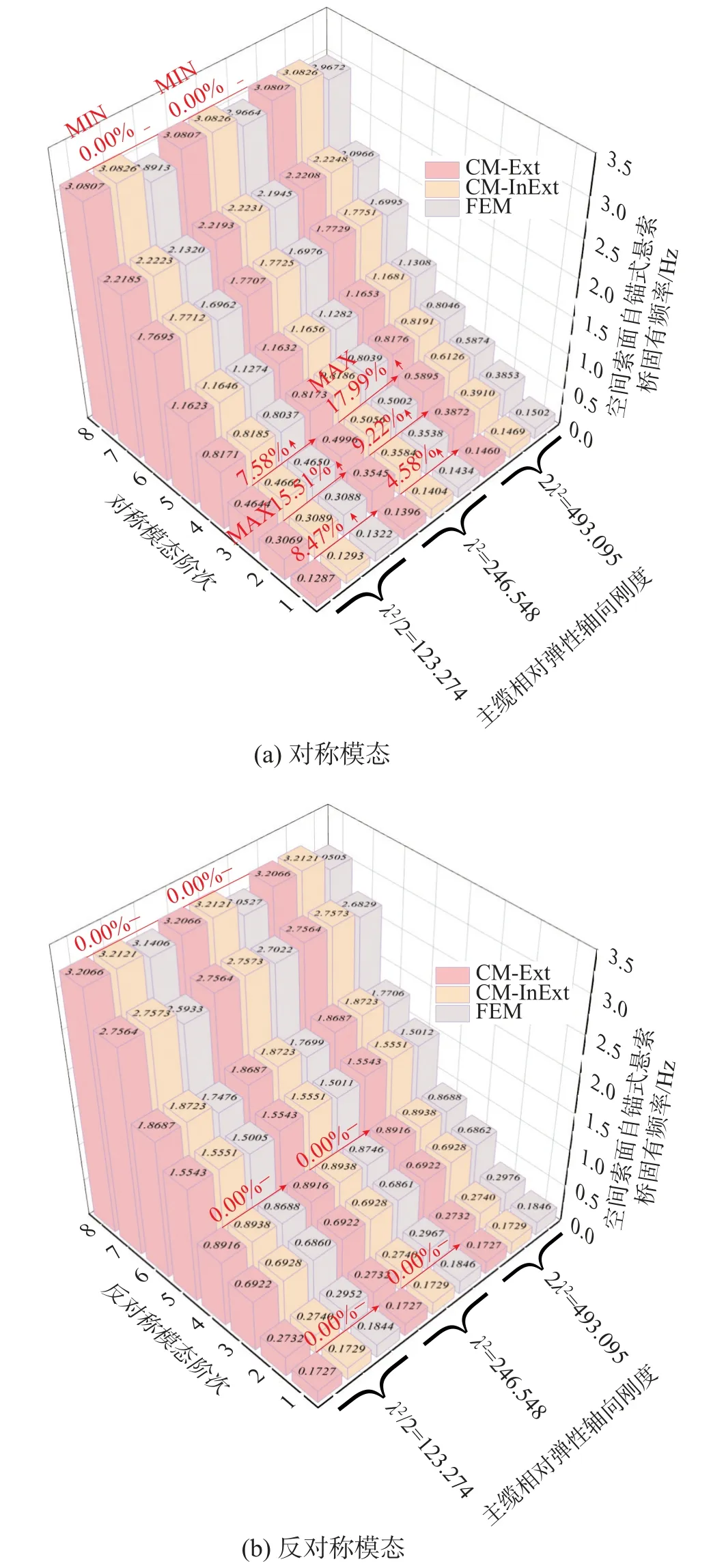
图11 主缆相对弹性轴向刚度对固有频率的影响Fig.11 Influence of the relative elastic axial stiffness of the main cable on natural frequencies

3.3.4 吊索相对弹性轴向刚度

图12 反映了空间索面倾角与是否考虑吊索拉伸效应的两类连续体频率差的变化关系。总体而言，不同空间索面倾角下，各阶次模态频率差变化规律基本一致，其中，对称模态最大频率差为索面倾角60°时的0.0069 Hz(图12(a))，反对称模态最大频率差为索面倾角90°时的0.0040 Hz(图12(b))。结果表明，吊索相对弹性轴向刚度与空间索面倾角敏感度甚为微弱。

图13 给出了 α2、λ2与是否考虑吊索拉伸效应的两类连续体模型频率差的变化关系。总体上，CM-Ext 计算得到的频率均低于CM-InExt，这反映了增大吊索相对弹性轴向刚度会提升部分结构刚度。对于对称模态而言，如图13(a)所示，当主缆相对弹性轴向刚度为2λ2时，3S 频率差达0.0231 Hz；而当主梁相对弹性抗弯刚度为5 α2时，8S 频率差达0.1088 Hz，其余各阶次频率差均低于0.0125 Hz。对于反对称模态而言，如图13(b)所示，各阶次频率差均不受λ2变动影响，当主梁相对弹性抗弯刚度为5 α2时，8AS 频率差则高达0.2128 Hz，CMExt 得出的频率6.9633 Hz 也更接近FEM 得出的6.8173 Hz，其余各阶次频率差均低于0.015 Hz。结果表明，吊索相对弹性轴向刚度与主缆相对弹性刚度关联并不密切，且仅影响低阶次对称模态；与主梁相对弹性抗弯刚度敏感度更为显著，尤其当 α2较大时，对高阶次模态影响较为强烈，反对称模态尤甚。相比于CM-InExt，CM-Ext 与FEM 计算结果更为吻合，结果也更为准确、可靠。

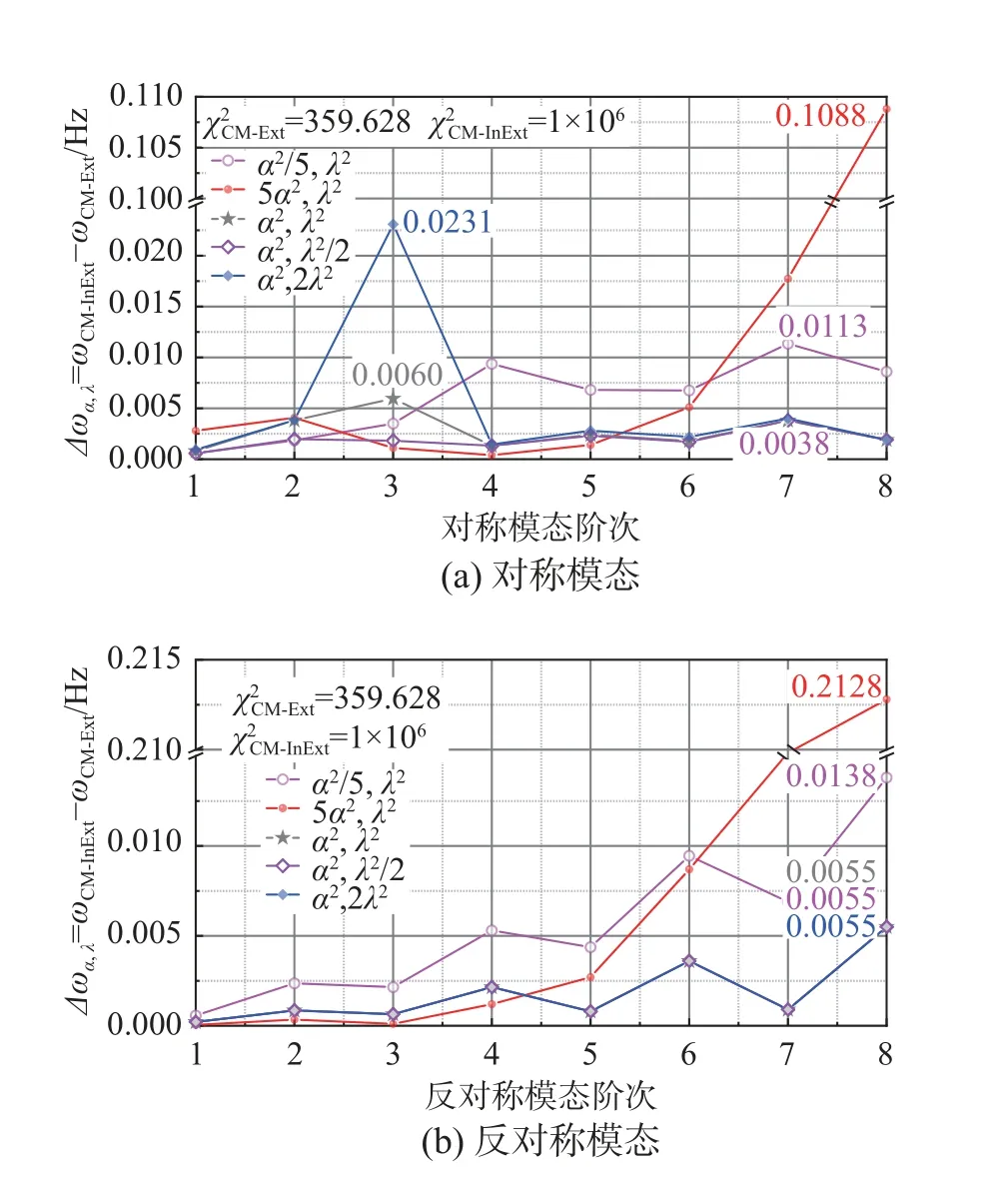
图13 主梁相对弹性抗弯刚度、主缆相对弹性轴向刚度与两类连续体模型(CM-InExt, CM-Ext)频率差的关系Fig.13 Relationship between relative elastic bending stiffness of the main girder, relative elastic axial stiffness of the main cable and frequencies difference of two types of continuum models (CM-InExt, CM-Ext)

4 结论

本文基于振动形态挠度理论，结合缆-索-梁空间耦合变形方程与相容方程，建立了考虑吊索拉伸效应的空间索面自锚式悬索桥连续体模型；为便于识别其动力特性，通过无量纲处理得到包含6 个无量纲特征参数和空间索面倾角在内的无量纲连续体模型；采用伽辽金求解方法求解模态频率与振型，结合数值算例和有限元模型验证其准确性，并对其中特征参数进行敏感性分析。得出以下结论：

(1) 空间索面自锚式悬索桥因其空间缆索耦合特性与子系统间的内部自平衡性与弹性协调性，使得建模分析过程冗长复杂；解析方法基于振动形态挠度理论，结合吊索拉伸效应的缆-索-梁空间耦合变形方程与考虑自平衡性的相容方程推导出可考虑吊索拉伸的无量纲连续体模型；力学机理清晰明确，高效解决了因其特性而造成非线性求解的难题。

(2) 吊索相对弹性轴向刚度χ2与主缆相对弹性轴向刚度λ2关联并不密切，仅影响低阶次对称模态频率；而与主梁相对弹性抗弯刚度 α2敏感度更为显著，尤其 α2较大时，是否考虑吊索拉伸效应将显著影响高阶次模态频率的准确性，反对称模态尤甚，故考虑吊索拉伸效应的连续体模型结果更为准确可靠。

(3) 吊索相对弹性轴向刚度χ2与空间索面倾角θ关联度较为微弱；各阶次频率受倾角的影响甚微，低阶次模态频率增幅随倾角增大而渐缓，高阶次模态频率则基本不受其影响，原因在于悬索桥面内主缆相对弹性轴向刚度仍近似一致。

(4) 主梁相对弹性抗弯刚度 α2将显著提升各阶次模态频率，且对高阶次对称模态频率与各阶次反对称模态频率影响更为强烈，随着 α2增大，模态间会出现交叉现象，需在动力设计中引起重视；主缆相对弹性轴向刚度仅对低阶次对称模态影响较为显著，而对反对称模态频率无影响。

与有限元模型相比，本文提出的连续体模型能高效准确地计算不同类型索面自锚式悬索桥的模态参数，进行动力特性的连续参数化敏感性分析，并作为工程初步设计、有限元模型修正和损伤识别的基准解析模型来提供必要前置数据。