基于蚁群- 改进人工势场法的移动机器人路径规划
2023-08-14任志伟胡平闫方曲富柱
任志伟,胡平,闫方,曲富柱
(河南科技学院信息工程学院,河南 新乡 453003)
众所周知,蚂蚁可以搬运大于自身质量的食物,另外它们还有一种特殊技能,即在寻找食物过程中,随着时间的推移,总能找到搬运食物的最优路径.蚁群算法最早是在1992 年由Dorigo 提出.他观察发现,蚂蚁在寻觅食物过程中总会释放一种信息素,蚂蚁之间通过建立起的信息素机制,确立蚁穴与食物之间的最优路径,并对路径形成记忆[1].
常用的全局路径规划算法有A*算法、蚁群算法、遗传算法和粒子群算法,常用的局部路径规划算法有人工势场法、速度障碍法和动态窗口算法等[2].其中蚁群算法具有稳定性高、可靠性强、独立性强等优点,但是由于该算法对信息素依赖较高,算法初期,若搜索范围较大,则信息素浓度较低,搜索效率低、算法运行时间长、收敛速度慢等缺点.人工势场法被广泛应用在自动巡航中,它主要依靠物体对目标点的引力和对障碍物的斥力规划路径,物体前进的方向是引力和斥力的合力方向.人工势场法的优点是数学模型简单、反应速度快等,但在靠近起始点位置由于引力过大而忽略斥力的作用使智能车和障碍物发生碰撞、出现目标不可达到以及局部极小值点问题等[3].
结合蚁群算法和人工势场法的特点,本文首先针对蚁群算法建模、仿真分析得到最优参数,同时针对人工势场法局部极小值等问题,通过引入相对目标距离进行改进.最后将蚁群算法和人工势场法融合,综合两者优点,通过建立数学模型、理论分析和仿真实验验证融合算法的改进效果.
1 栅格地图建模
根据障碍物的获取程度不同,移动机器人路径规划可分为局部规划和全局规划两种.本文讨论全局规划.全局路径规划需要预先知道环境的完整信息,指在具有静态障碍物的环境中依据某些性能指标,在空间中找到一条从起始状态到目标状态的无碰撞路径,是一种静态规划算法[4].常见的机器人全局路径规划建模方法包括:栅格地图法、拓扑法、可视图法等.
栅格地图法作为最为常见的路径规划建模方法之一,具有模型简单、后期维护容易等特点,主要原理是将地图上划分为若干个网格,每一网格代表障碍无法通行或无障碍通行自由,每个栅格大小相同,即障碍物栅格和可通行栅格相同,同时障碍物大小位置在机器人行走过程中不发生变化.在栅格地图中,在当前节点i 位置路径决策可选方向有“十”字型或“米”字型,本文采用“米”字型方向选择规则[5].栅格地图建模如图1 所示,在MATLAB 软件中设置宽和高均为20 的地图,阴影格代表障碍物分布位置,空白格代表机器人可以自由通过的路径.

图1 栅格地图建模Fig.1 Grid map modeling
设置传递因子的值为1 或者0,障碍物值设置为1,自由通行值设置为0.则栅格地图可以用数学模型表示为
式(1)中机器人从起点到终点过程中可以由8 个方向前进,即上、下、左、右、左前、左后、右前、右后.机器人在横向或者纵向上每行驶一步距离为1,在斜着行驶时距离为.
2 基于蚁群算法数学建模及仿真分析
2.1 蚁群算法基本概述
蚁群算法是一种群体智能仿生优化算法,是根据自然界中蚂蚁获取食物的过程而开发的,因此又称为蚂蚁算法[6].蚁群算法主要是蚁群依赖于信息素浓度来实现的,蚁群算法原理如图2 所示,通过模拟蚁群寻找食物过程来分析蚁群算法的基本原理.假设蚂蚁释放的信息素浓度一定,信息素的挥发速度一定,假设蚁群从A 点出发到终点E,C 到F 路径不通, 那么蚁群从A 到E 共有两条路径即ABCDE 和ABFDE,假设蚁群数量一定,BC=CD=5,BF=FC=2.那么实验开始,蚂蚁从两条路径路过的数量基本相同,但随着时间的推移,蚁群在ABFDE 上的数量逐渐增多.这是由于该路径的路径较短,一定时间内蚁群释放的信息素浓度增高,从而使蚁群趋向该路径.
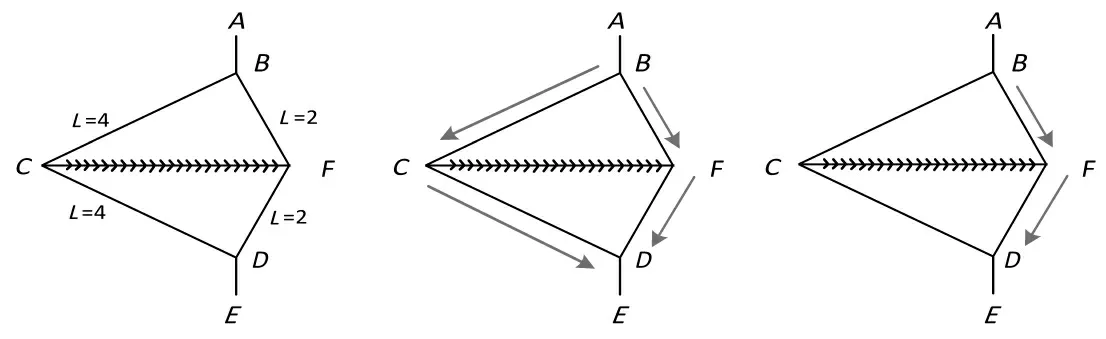
图2 蚁群算法原理示意Fig.2 Schematic diagram of ant colony algorithm
2.2 蚁群算法的数学建模分析
本节通过建立蚁群算法的数学模型来分析各个参数对于该算法的影响.蚁群搜索路径可以作以下假设:首先假设共有M 只蚂蚁参与路径搜索,各个路径开始的信息素浓度等于常量C,那么从X 到Y 的信息素浓度为C 可以表示为τAB(0)=C(C 为常数).第k 只蚂蚁(k=1,2,3...,M)共走了t 步,那么它从X 点到Y 点的概率可以表示为
式(2)中:表示t 时间是X 至Y 上的信息素浓度,ak表示蚂蚁下个时间可以到达地方的集合,tabu(k)表示蚂蚁之前路过的地方,为X 到Y 点的启发函数,它是蚂蚁从X 到Y 点发生概率的重要参数,它可以表示为
式(3)中:dXY表示地点ηXY之间的距离.这里不难看出dXY越大则ηXY越小,进而越小;而越大则越大.蚂蚁从X 到Y 的概率和两者间的距离成负相关,和信息素浓度的大小成正相关.
蚁群从开始到结束,在这个过程中,既要考虑到释放信息素△τX(Yt),也要考虑到挥发的信息素,假设挥发系数为ρ(0<ρ<1)信息素浓度更新可以表示为
由公式(4)可知,信息素浓度更新等于挥发后的信息素浓度加上新增的信息素浓度,挥发系数ρ 和信息素浓度呈负相关作用.在实际应用中,该系数过大时,信息素浓度挥发加快,机器人的全局搜索能力降低,算法收敛越慢[7];而当该系数过小时,信息素挥发减慢,机器人选择不同路径的概率降低,不利于发现最优路径.
式(6)中:LK表示XY 的距离.信息素浓度Q 是指没完成一次循环结束之后的总信息素浓度.每轮迭代后会更新蚂蚁找到的所有路径上的信息素,导致信息素积累过快,算法容易陷入局部最优[8],适当的信息素浓度是保证蚁群算法全局搜索能力的前提.
2.3 通过仿真分析得出最优参数
传统蚁群算法流程如图3 所示.
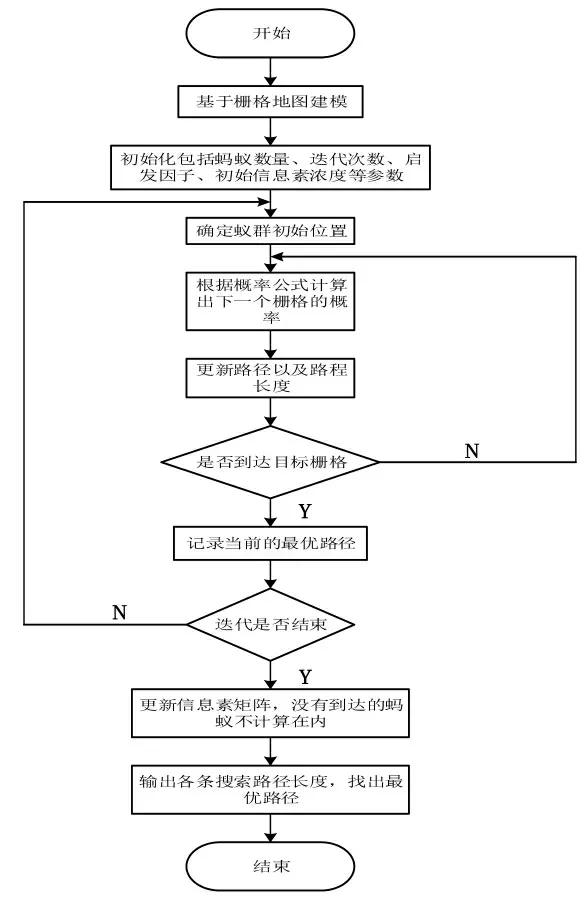
图3 传统蚁群算法流程Fig.3 Flow of traditional ant colony algorithm
调整蚁群数量M,仿真运动轨迹和仿真迭代曲线如图4 所示,确定蚁群数量合适区间要注意参数的选择对于蚁群算法的效率和精确度有很大影响.首先是蚂蚁数量的选择,蚁群大小直接影响搜索效率.若蚁群数量过小,无法遍历全地图获取全局最优路径[9];若蚂蚁数量过多,则会引起信息素浓度过高,不同路径之间的信息素浓度差值太小,导致实验结果不理想,因此需要选取合适的蚂蚁数量.
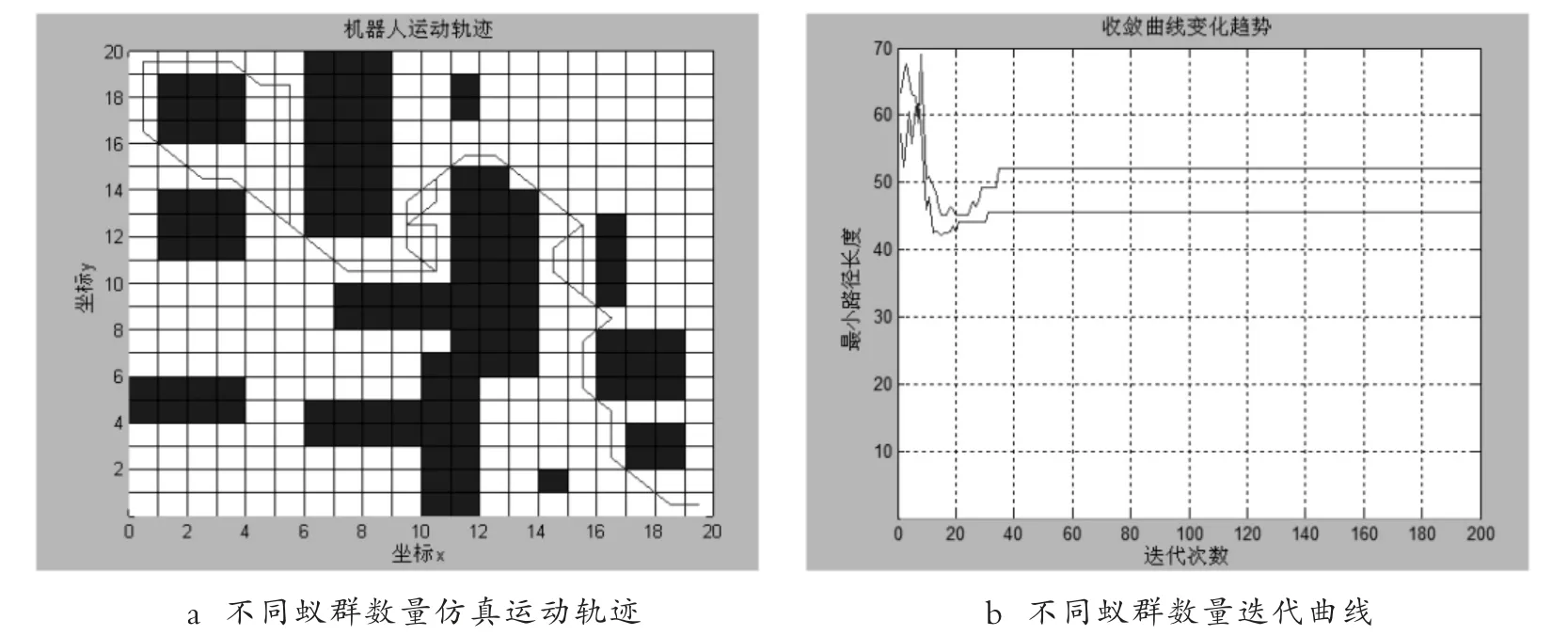
图4 不同蚁群数量运动仿真结果Fig.4 Simulation results of movement of different ant colonies
经过多次实验发现蚁群数量在90~120 时候, 蚁群算法规划的路径和迭代次数逐渐达到理想状态,当M=90 时,在迭代约37 次时趋于稳定,但最小路径长度为52.增加蚂蚁数量,当M=120 时,最短路径由52 变为44,迭代次数也由38 变为34.调整信息浓度因子α的值,对比运动轨迹和收敛曲线图,确定信息素浓度区间值.
通过改变信息素浓度,仿真运动轨迹和仿真收敛曲线如图5 所示.信息素浓度因子α会影响蚂蚁选择该路径的概率,当α太大时候,蚂蚁就更倾向于选择其他蚂蚁选择过的路径,搜索的随机性减弱,同时降低了解的多样性,扼杀了一些地图中找到全局最优解的概率会加快收敛速度[10],α太小则搜索能力下降,随机性增大,因此适当的信息素浓度因子对于路径规划具有重要作用.
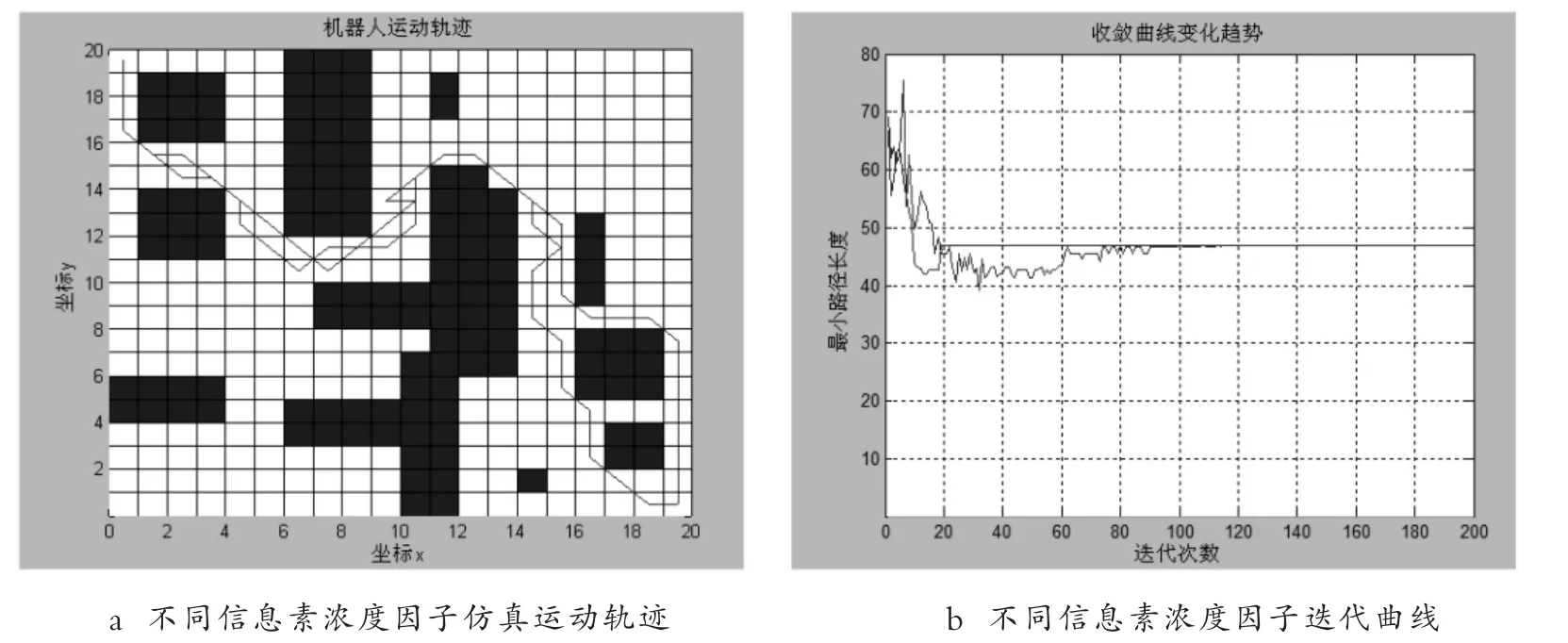
图5 不同信息素浓度因子运动仿真结果Fig.5 Simulation results of different pheromone concentration factors
通过改变α的值观察MALAB 仿真测试结果,当α的值等于1 的时候,迭代次数约为110 次,此时收敛曲线不满足实际需求.随着α值增大,迭代次数逐渐减小,当α的值等于2 时,迭代次数约为20 次.上述通过改变α的值验证了实验猜想,与预期结果一致,因此α的值需要适中,才能以最快速度和最优路径到达终点.
调整最短路径因子β,仿真运动轨迹和仿真收敛曲线如图6 所示.β 作为最短路径因子,它反映了机器人在不同路径中选择最短路径的因子,是机器人实现最优路径的一项重要参数.当β 过大时,蚁群更趋向于搜索较近的下一节点,随机性降低,算法容易陷入局部最优[11].当β 过小时,则搜索路径变长,无法达到理想路径.
在MTLAB 仿真实验中,改变最短路径因子β 的值,当β 的值为3 的时候,机器人路径规划距离为82,迭代次数为21,规划距离较远.而当β 的值为5 的时候,机器人的路径规划距离为60,迭代次数为40.
通过改变不同参数,观察移动机器人运动轨迹和迭代次数,确定了参数值的区间范围,但在实际应用中,各个参数之间也存在着紧密的联系.通过多次仿真实验得出最优参数,当M=110,α=1.4, β=3.5,ρ=0.4,Q=1 时移动机器人在最优路径上.机器人路径轨迹和收敛曲线变化如图7 所示.
通过改变栅格地图模型,该算法仍然可以运算出预期的结果,经典蚁群算法运动仿真结果如图8 所示.
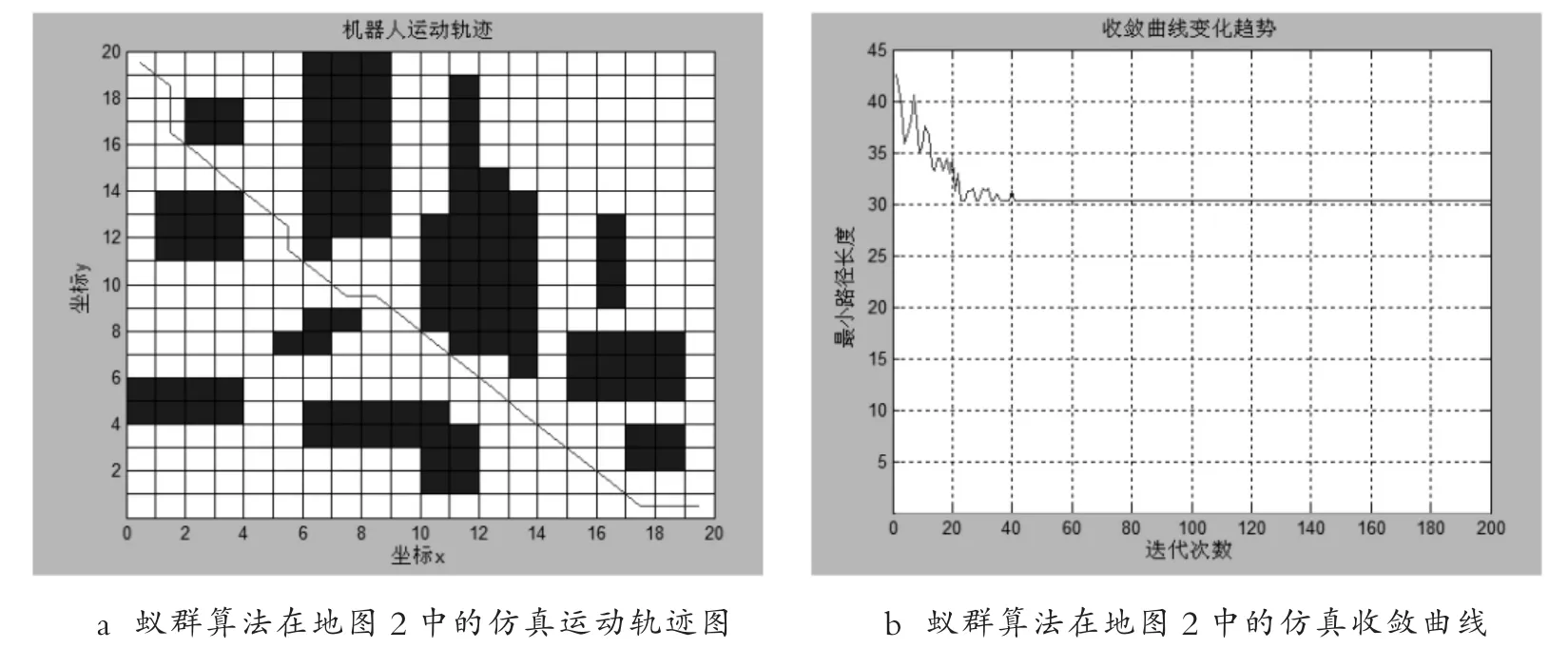
图8 经典蚁群算法在地图2 中运动仿真结果Fig.8 Motion simulation results of classic ant colony algorithm in map 2
3 人工势场法的改进
3.1 经典人工势场法的函数构造
人工势场法是一种比较常见的机器人局部路径规划的算法, 它的基本原理是利用人工势场制造一种引力和斥力,利用“同性相斥,异性相吸”的物理原理来描述目标点和障碍物在机器人运动过程中对其产生的作用[12],引力是机器人到目标点方向,斥力则是障碍物到机器人方向,机器人在势场中所受到的合力方向则是前进的方向.移动机器人在人工势场中的受力情况如图9 所示.
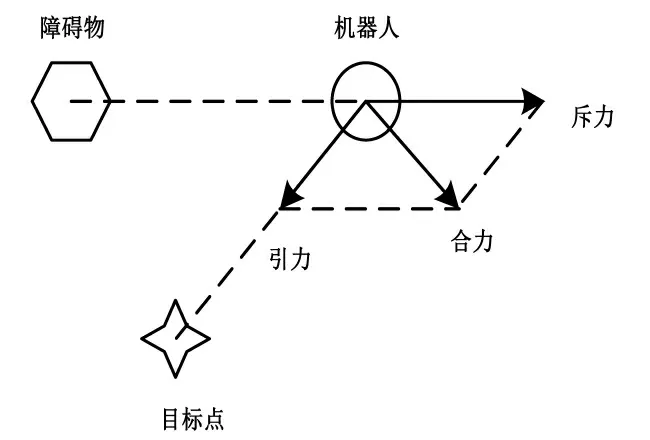
图9 移动机器人在人工势场中的受力情况Fig.9 Force of mobile robot in artificial potential field
假设机器人在势场上受到的引力为Uatt,受到的斥力为Urep,那么机器人受到的合力可以表示为
其中引力场函数可以表示为
式(8)中:Xg表示目标所在位置,X 表示移动机器人当前位置,Katt是引力常数.那么机器人所受引力可以表示为
式(9)中:d(X,Xg)表示终点和移动机器人的距离,是单位向量,方向是从移动机器人到终点.可以得出,引力的大小和机器人到目标点的距离呈正相关.引力场场强随着机器人与目标点的距离减小而减小,直到机器人到达目标点时,引力势场为零[13].
移动机器人的斥力场函数可以表示为
式(10)中:d0表示移动机器人和障碍物的最远距离,若机器人离障碍物的距离大于d0,则可以忽略斥力作用.
斥力场函数做负梯度运算可以得到机器人在斥力场所受的斥力,它可以表示为
因此移动机器人在势场内所受到的合力可以表示为
由上述分析可以得出,人工势场法存在很多的优点.和一般的导航算法比较可以得出,它具有计算速度快、效率高、数学公式简洁等优点.但在某些特定情况下也存在着一些问题,这些问题是:
第一,目标不可达问题[14].当机器人在靠近终点时,会存在斥力大于引力的情况,使得目标点无法到达;
第二,陷入局部极小值.机器人在势场中受到合力的方向决定了移动的方向,若在某点移动机器人受到的合力为零,即引力等于斥力的情况,则机器人无法移动或徘徊不前.
3.2 改进人工势场法
3.2.1 目标不可达问题 当移动机器人到达某个点后,由于斥力大于引力作用,无法到达目标点,通过引入目标点相对距离d(X,Xg),新的目标点可以对移动机器人增加吸引力,从而使移动机器人所受合力方向发生改变.
重新定义斥力场函数
对斥力场函数(13)做负梯度运算得
式(13)中
移动机器人在改进人工势场中的受力情况如图10 所示.
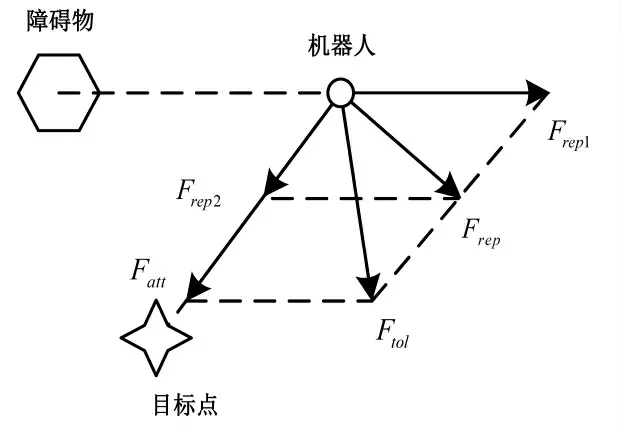
图10 移动机器人在改进人工势场中的受力情况Fig.10 Force situation of mobile robot in improved artificial potential field
通过引进目标点相对距离,机器人受到的引力增大,合力方向发生改变,机器人可以继续向目标点进行移动.此时,移动机器人所受合力方向可以表示为
3.2.2 局部极小值问题 当机器人在势场中出现受力平衡无法移动时,可以使用障碍转移的方法,使机器人摆脱当前引力大于斥力的情况.具体操作步骤如下:
第一步,当机器人无法移动时,通过确定机器人和目标点位置后将其连接为一条线;
第二步,以移动机器人到目标点为底,通过障碍物作垂线,并标记此垂线上离障碍物最近点P;
第三步,连接机器人和点P,此路径即为移动机器人暂时通过的路径.
机器人障碍转移分析如图11 所示.
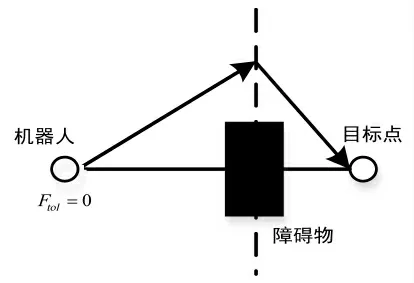
图11 障碍转移机器人受力示意Fig.11 Stress diagram of obstacle transfer robot
改进的人工势场法的算法流程如图12 所示.
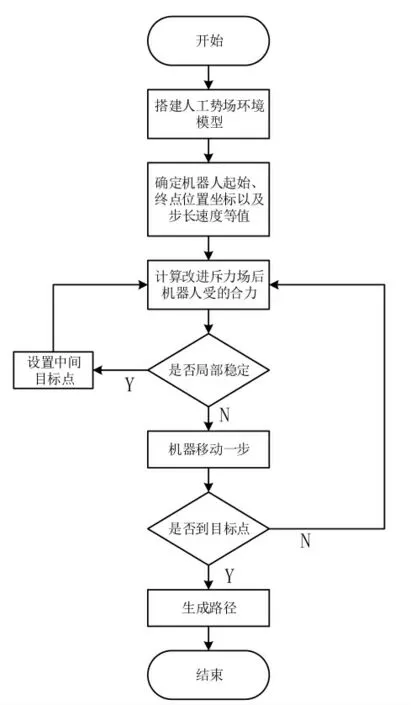
图12 改进人工势场法算法流程Fig.12 Algorithm flow of improved artificial potential field method
4 混合算法流程及仿真分析
4.1 人工势场法思想和蚁群算法结合算法
4.1.1 算法的基本原理 在路径规划初期,通过改进后的人工势场法,规避存在目标点无法到达和局部极小值问题,并改善蚁群算法前期的盲目性搜索,同时改进后的融合算法增加信息素浓度差异,随着信息素浓度增大,弱化人工势场法的作用,充分发挥蚁群算法作用,使移动机器人路径规划在最短时间内达到全局最优路径.
传统的蚁群算法中,蚂蚁k 从X 点到Y 点的概率可以表示为
式(18)中:启发因子ηX(Yt)=1/dXY,它表示蚂蚁从X 到Y 点的概率,它的大小与距离呈负相关,引入另外一个因子,使它与移动机器人受到合力以及迭代的次数相关,可以表示为
式(19)中:D 表示为当前蚁群迭代次数,Dmax表示为蚁群的最大迭代次数.cosθ 表示为移动机器人当前可以移动的方向与受到合力方向夹角的余弦值.
此时蚂蚁k 从X 到Y 点的概率公式表示为
式(20)中:γ为调节因子,不难发现,在前期迭代次数较小时,该因子在选择路径中起着较大作用,此时人工势场在移动机器人路径规划中发挥主要作用.上式中合力即为
4.1.2 融合算法中, 移动机器人在栅格地图中的受力分析 机器人的可能移动方向分析如图13 所示,在栅格地图中,若没有外力左右机器人可以往八个方向移动,当移动机器受到合力为Ftol,此时机器人可能移动方向为左方或者左下方,那么按照合力方向和可移动方向夹角的余弦值与ηFtol的关系可得知,机器人会往角度越小的方向走,即机器人会移动到左下方.
4.1.3 算法实现步骤 与传统蚁群算法相比,融合后的算法加入了人工势场法作用,在算法开始需要初始化除蚁群数量、迭代次数、启发因子、信息素浓度,也要包括引力常量和斥力常量.通过融合算法概率公式计算出移动机器人在栅格地图中规划的所有路径,最终筛选出最优路径.蚁群- 改进人工势场融合算法流程如图14 所示.
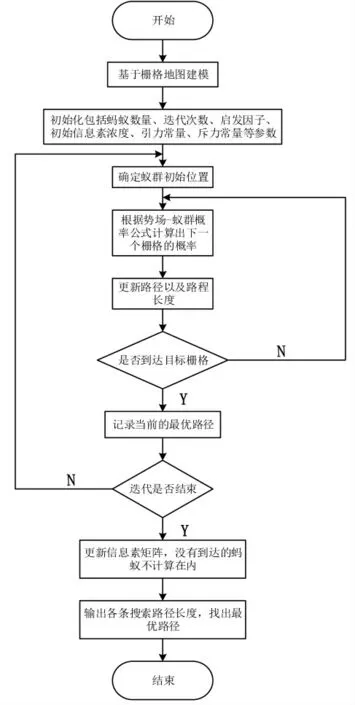
图14 蚁群-改进人工势场融合算法流程Fig.14 Ant Colony-improved artificial potential field fusion algorithm flow
4.2 混合算法仿真与分析
通过MATLAB 软件对改进后的融合算法进行仿真实验,同时在蚁群数量、迭代次数、启发因子、信息素浓度等参数一致的情况下,对比两个算法运算不同的栅格地图,分析不同地图下两者算法运算结果.而参数优化一般使用专家经验或反复实验确定,使用控制变量法对蚂蚁数量M、信息素影响因子α、启发信息影响因子β、挥发系数ρ、信息素强度Q 进行优选[15].在前文中通过多次模拟得出,当蚁群数量M取值110、信息素因子α取值1.4、启发因子β 取值3.5、挥发系数ρ 取0.4、信息素常量Q 取值1 时.传统蚁群算法下仿真运动轨迹和仿真收敛曲线如图15 所示;改进蚁群算法下仿真运动轨迹和仿真收敛曲线如图16 所示.
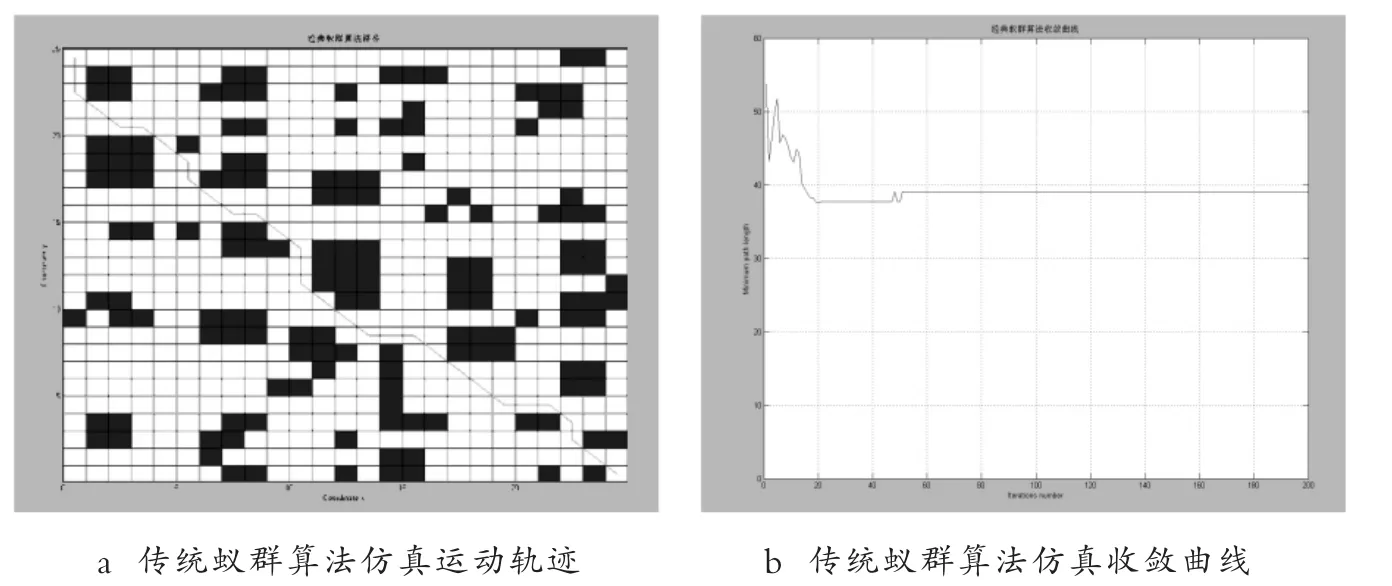
图15 传统蚁群算法在25*25 栅格地图中的运动仿真结果Fig.15 Simulation results of traditional ant colony algorithm in 25*25 grid map
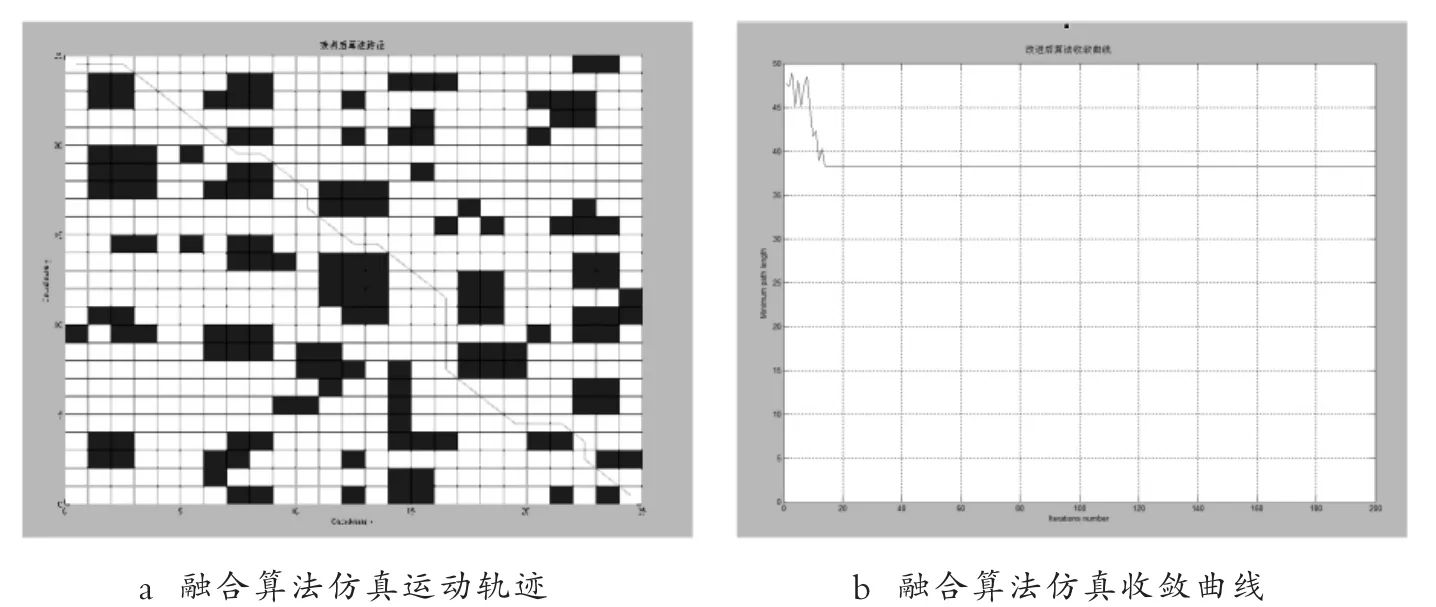
图16 融合算法在25*25 栅格地图中的运动仿真结果Fig.16 Motion simulation results of fusion algorithm in 25*25 raster map
改进后的蚁群算法和传统蚁群算法运算后的各项数据对比如表1 所示,在同等条件下,融合算法在最优路径规划长度上缩短了1,在路径最远长度上缩短了13,迭代的平均次数缩短了21,平均运行时间缩短了3.5 ms,各项参数都有较大提升,改进后的融合算法要优于传统蚁群算法.

表1 传统蚁群算法和融合算法各项数据对比Tab.1 Comparison of various data of traditional ant colony algorithm and fusion algorithm
5 小结
本文介绍了经典人工势场法的基本原理,通过引入目标相对距离和中间点方法,对移动机器人的斥力场函数进行改进,解决了人工势场法目标无法到达和陷入极小值问题.通过在栅格地图中进行建模、仿真,分析了蚁群算法的优缺点.在传统蚁群算法的基础上引入改进势场函数,重新构造具有势场因子和信息素浓度的复合函数,解决了蚁群算法中存在前期搜索速度慢、陷入局部最优问题.通过MATLAB 仿真分析进一步验证了融合算法在最远路径、最优路径、运行时间、迭代次数各项数据都优于传统蚁群算法.
