圆偏振非谐波双色场产生太赫兹辐射理论研究
2023-08-14倪铭陈曦卢晨晖
倪铭,陈曦,卢晨晖
(上海工程技术大学机械与汽车工程学院,上海 201620)
太赫兹波(Terahertz,THz)是指波长在0.03~3.00 mm,频率范围为0.1~30.0 THz(1.0 THz=1012Hz)的电磁波.由于其在电磁频谱中的特殊位置介于微波与红外之间,因此赋予了其不同于其他电磁波的特殊光谱性质,如低能性、强穿透性、宽带性等,从而成为目前电磁波段中最具开发潜力的波段[1].太赫兹波在基础物理学、材料、通信、工业无损检测等领域有着广泛的应用前景[2-5].目前产生太赫兹辐射的方法主要有光电导天线法[6]、非线性晶体整流法[7]、气体等离子体等[8].在这些方案中,利用超快激光诱导气体等离子体是产生高强度宽带太赫兹辐射的理想选择, 因为利用气体介质可以有效避免非线性晶体和光电导材料所带来的损伤阈值问题,并且能够有效地降低THz 辐射在长距离传播时的介质吸收,产生的太赫兹辐射频谱范围可覆盖0~150 THz 甚至可以更高[9].目前最新研究报道利用双色圆偏振同旋激光场(CP-S)产生的太赫兹辐射相比于传统线偏振平行双色场,辐射强度整整提高了8 倍[10].
此外,灵活地控制宽带太赫兹频谱形状和偏振特性对于科学研究和太赫兹应用有着重要意义,例如基于宽带可调谐的太赫兹波能够激发物质的低激发态,改变物质的电磁特性和光学特性[11],对电子进行加速、压缩、聚焦,使得强场太赫兹非线性物理学的研究成为可能[12];并且在城市地铁、机场的安检等实际应用领域,灵活地调整太赫兹的频谱可以有效地提高对不同物质检测的正确性.2021 年,Fan 等[13]从实验和理论两方面证明了利用波长可调谐的光参量放大激光器(OPA),可以对太赫兹频谱进行有效调制,将太赫兹中心频率从4 THz 移动到38 THz.2022 年上海交通大学Wang 等[14]利用四分之一波片(QWP)来改变双色场中基频光的偏振状态,实现太赫兹的中心频率从0.56 THz 移动到了0.82 THz.他们的分析结果表明太赫兹的频谱变化是由于在双色场的光丝内部传播的过程中双折射现象引起的双色场偏振态的改变.
本文在同旋向圆偏振光的基础上对倍频光场进行调谐, 利用二维光电流模型研究太赫兹辐射的特性.数值模拟表明,在此双色场作用下,通过对双色激光场二次谐波(SW)中心频率的调谐,能够在保持太赫兹辐射基本不变的基础上,实现太赫兹辐射频谱的操控,太赫兹频谱中将出现高频部分,并且其强度可以得到有效控制.除此之外,太赫兹辐射的偏振特性也能够因此而改变,实现了从近似线偏振到圆偏振的变化.最后利用局部电流模型(LC)理论分析了频谱调制和偏振变化背后的物理机制.
1 理论模型
1.1 二维光电流模型
由基频波(FH)与倍频波(SW)组成的双色超快飞秒激光电离气体产生太赫兹辐射的物理机制通常由光电流模型(Photo-current Model)来解释[15].因此采用光电流模型理论模拟了飞秒激光与气体介质相互作用产生太赫兹辐射的动力学过程,考虑到圆偏振的光场情况,将光电流模型表示成二维模型.在此模型下激光电离气体产生太赫兹辐射分为两个阶段:第一阶段,气体介质在超快飞秒激光作用下产生自由电子;第二阶段,自由电子在外部电场加速震荡下形成随时间变化的光电流,并向外辐射太赫兹波.
当超快激光与气体介质相互作用时,气体中的分子会被电离,根据激光功率的高低气体的电离机制也会有变化,有隧穿电离(TI)、多光子电离(MI)、越垒电离(OTBI)等.为了判断在气体电离过程中,哪种电离过程占据了主导地位,引入Keldysh 参数,它代表电子隧穿势垒的时间与激光光学周期的比值,由式(1)计算
式(1)中:Ui为气体的电离势能,Up为激光的有质动力能:,该值的大小受到激光中心频率以及电场振幅的影响.通过计算出的 Keldysh参数值大小来判别具体是哪种电离过程占据了主导地位,当γ<1 时,是隧穿电离(Tunneling Ionization)占据主导地位,而当γ>1 时,由于激光电场强度小于原子得库伦场强,因此主要受多光子电离(Multi-photon Ionization)的影响.在我们的计算模拟中,基频波的中心波长为800 nm,脉宽τ为60 fs,激光强度设置为2.2×1014W/cm2,根据式子(1)和文献[16]中的实验结果得到γ<1,所以在整个气体电离过程中是隧穿电离(TI)占据了主导地位.
1.2 电子电离率
关于隧穿电离的计算,主要有两个物理模型:①静态隧穿电离(Quasi Static Tunneling Rate),②ADK(Ammosov-Delone-Krainov)隧穿电离,两种模型的计算结果十分相似,在这里选择静态隧穿电离模型(QST),其电离率WST可由式(2)计算
式(2)中:ε(t) =E(t)/εa,εa为原子单位下的电场强度,ωa为 激光频率的原子单位,ωa=k2me4/ ℏ3≈4.13*1016s−1,rH为气体分子的电离势能,rH=Uion/UionH,氢原子的电离势能UionH≈ 13.6 eV,氮气UionN≈15.6 eV.
1.3 瞬时电流
当得到气体分子的电离率WST后,根据电子速率方程(Electron Source Equation),可计算出电离电子密度随时间的变化速率N e(t)
Ng为气体的初始密度,我们定义气体介质最终的电离几率为
气体分子经超快激光电离后形成自由电子,在电离初始时刻t’时自由电子的速度为0,在外部电场作用下形成快速振荡加速运动,在之后的每一个时间段 (t’,t)内,自由电子的漂移速度可由式(5)计算
式(5)中:e 为基本电荷,me为电子质量,考虑在双色激光作用下所有时间段内产生的自由电子共同作用,得到气体分子电离产生的总横向电流
dNe(t’)代表了在(t’ ,t’+dt)时间间隔内的电子密度变化率,根据麦克斯韦方程可知,电磁辐射强度应正比于电流J(t)对时间t的一阶导.
对其取傅里叶变换可得到太赫兹的频谱E THz(ω) ,再对E THz(ω)进行傅里叶逆变换后可得到太赫兹的时域分布ETHz(t).
最后通过对太赫兹频谱积分而得到太赫兹辐射的总强度.
2 计算结果与理论分析
2.1 任意偏振双色激光场描述
为了不失一般性,设由基频波(FH)与二次谐波(SW)组成的任意偏振双色高斯矢量激光场可由式(9)表达
式(9)中:r 为基频波(FW)与二次谐波(SH)之间得强度比值系数,为总的光场强度,φ为基频波(FW)和二次谐波(SW)之间的相位角,ρ为激光的椭圆率(− 1 <ρ<1),θ为两个正交光场分量之间的相位延迟,双色激光场的偏振状态可由这两参数调控.四种偏振状态的双色场激光参数分别为(:1)双色线偏振平行(LP-P):ρ1=ρ2= 0,θ= 0(,2)双色线偏振正交(LP-O):ρ1= 0,ρ2=+∞,θ=0,(3)双色圆偏振同旋(CP-S):ρ1=ρ2= 1,ε= 1,θ=± /2,(4)双色圆偏振反旋(CP-O):ρ1=ρ2= 1,ε= −1 ,θ=±/2,双色激光的强度比例系数r 和相位φ角分别固定为10%和 0.5.
2.2 二次谐波波长调谐对太赫兹频谱的影响
基于上述设置的激光参数初始条件,首先研究了双色场二次谐波(SW)中心频率变化对激光电场包络形状的影响,对比标准倍频和二次谐波(SW)经过负调谐后的双色激光电场时域波形.图1 展示了二次谐波(SW)中心波长为400 nm 和395 nm 时双色激光电场时域包络形状,可以看出当二次谐波(SW)的中心频率经过负调谐后,激光脉冲包络的对称性被打破,从原来对称的高斯型变成了强度受调制的状态,这是由于二次谐波中心波长经过调制,双色光场在合成中振幅发生了改变,导致电场包络形状发生了整体变化,但是激光电场峰值并没有下降很多.此外,从图1 还可以看出,随着二次谐波中心波长的改变,激光的偏振形态由规则的圆形变为了在传播过程中圆形中心位置不断改变的圆偏振形态, 这将进一步影响电流的运动.
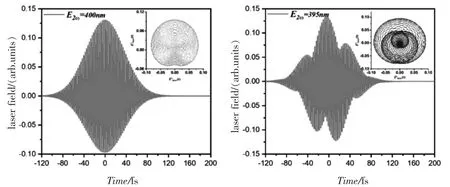
图1 同旋向标准双色场和非谐波双色场的时域波形(单方向)以及偏振图Fig.1 The waveforms of the standard and the tuned second harmonic two-color circularly polarized laser pulse with the same helicity in one direction
在图2 中,计算了当二次谐波经过调制之后,瞬时电流J(t)的变化情况.其中灰线对应着标准双色场的情况,二次谐波的中心波长为400 nm,红线对应着非谐波情况.从图中可以看出,光电流随着激光场震荡, 其尾部有明显的非零直流项.当将二次谐波的中心波长做微调, 从原来的400 nm 改变到395 nm,瞬时电流整体的形状不发生明显的变化,不过非零直流项的强度发生了一点减弱.该电子电流的运动在亚皮秒的量级,并且电流非零的部分对应着太赫兹辐射的强度,由此可知,随着瞬时电流的变化,太赫兹辐射的强度将发生改变.
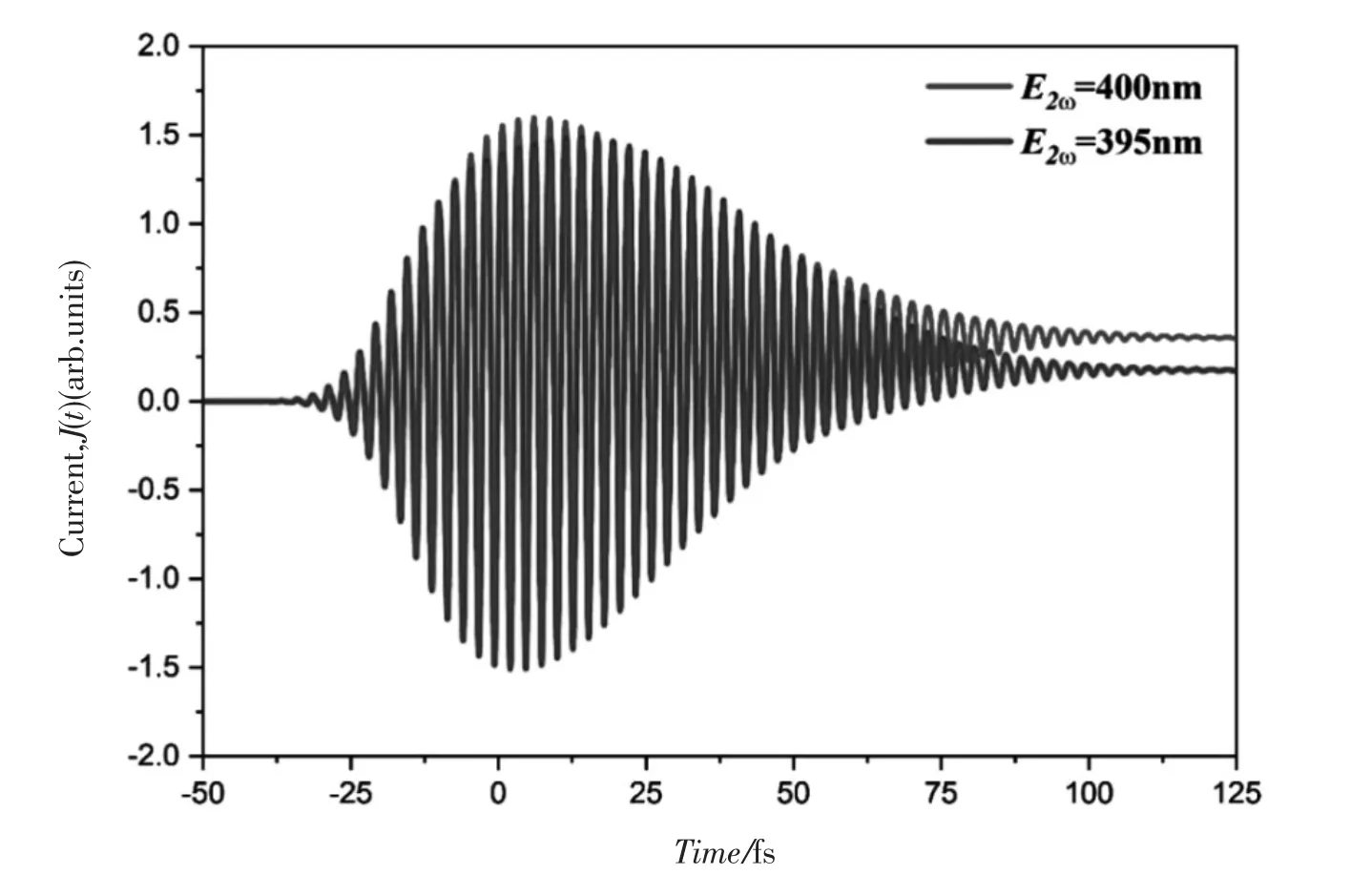
图2 标准双色场和二次谐波调谐的双色场对应的瞬时电流图Fig.2 The transient electron currents for the standard and tuned second harmonic two-color circularly polarized laser pulse
为了更好地研究二次谐波中心频率的变化对产生太赫兹辐射频域和时域的影响, 将二次谐波调谐的范围进一步扩大.在图3 展示太赫兹频谱随着中心波长的变化,从图中可以看出,在标准倍频情形下太赫兹的频谱在高频处分量几乎为0,其频谱范围主要在0~45 THz.而随着二次谐波(SW)中心波长的负调谐,频谱的高频分量逐渐出现在太赫兹频谱范围内,同时低频分量被抑制住,将中心波长调整到385 nm 时,太赫兹频谱的高频分量振幅提高了30%,并且太赫兹高频峰值的中心也从70 THz 移动到了80 THz.
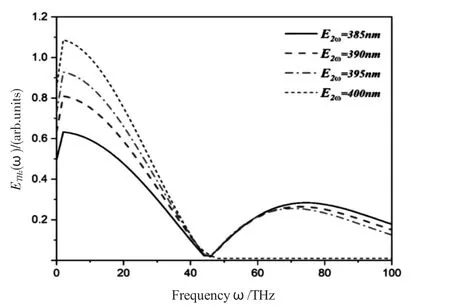
图3 不同二次谐波波长下的太赫兹频谱图Fig.3 The THz spectrum for the circularly polarized two-color laser pulses with different second harmonic wavelength
2.3 圆偏振太赫兹辐射产生
在观察到频谱变化规律后,继续探究太赫兹时域波形的偏振极性变化,对图3中的太赫兹频谱ETHz(ω)进行傅里叶逆变换,测量了二次谐波(SW)中心波长在400 nm,395nm,390 nm,385nm时的太赫兹三维时域波形.如图4所示,其中红色为太赫兹电场在水平方向上的分量ETHzx(t),绿色为垂直方向上的分量ETHzy(t),黑色为两个方向上合成随时间变化总的太赫兹三维时域波形.可以看到在标准倍频情况下,太赫兹辐射的偏振状态是线性极化的,测得椭圆度ε=9%,这与文献[17]中的实验的结果一致,然而当对二次谐波(SW)中心波长做一定的调谐,变为395 nm 时,太赫兹的偏振特性发生了显著的变化,垂直方向上ETHzy(t)的振幅值从-0.05变成了-0.15,最终合成产生了椭圆度ε=66%的圆偏振太赫兹辐射,随着波长的继续调制,水平方向的太赫兹ETHzx(t)也发生了变化,太赫兹辐射的椭圆度稳定在60%左右.相比于利用特殊光学元器件和复杂激光场配置,能够更灵活地实现太赫兹偏振特性的实时控制.
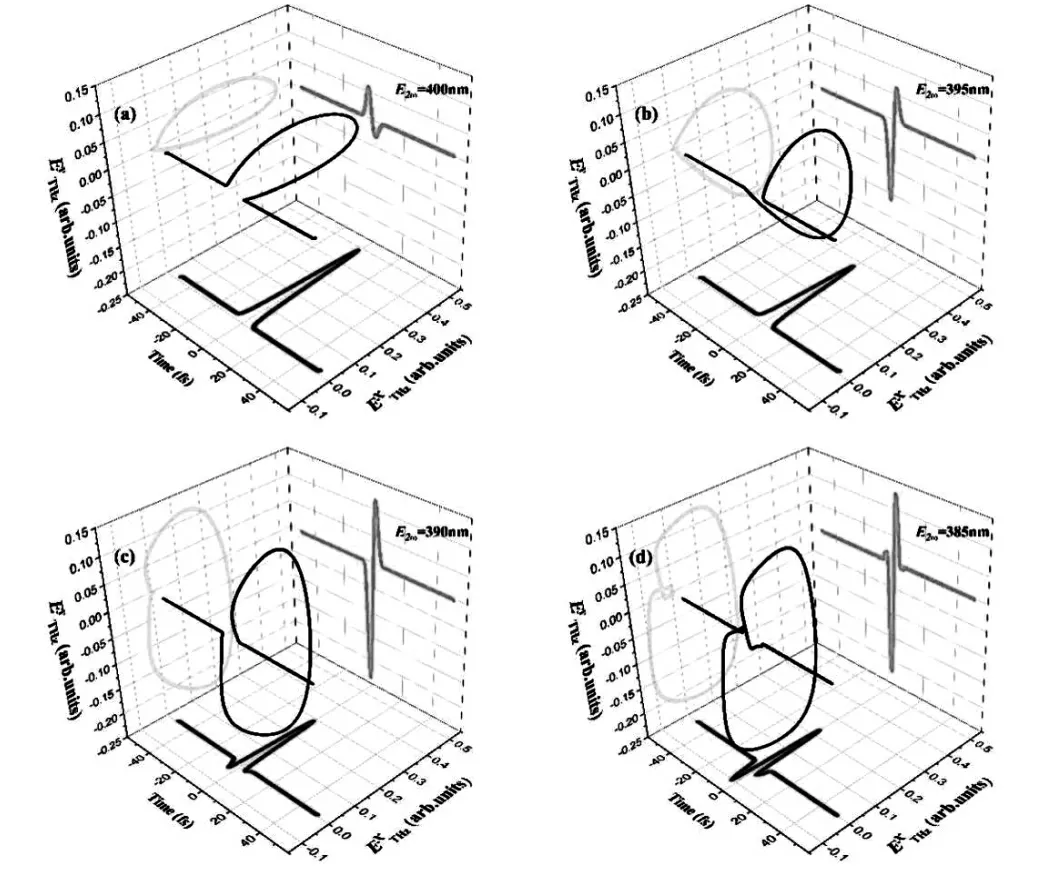
图4 太赫兹的波形和偏振和调谐波长的变化图Fig.4 The THz waveform and polarization states for the circularly polarized two-color laser pulses with different second harmonic wavelength
2.4 局部电流模型理论分析
为了清楚地解释倍频波中心波长调谐导致太赫兹频谱以及偏振特性变化背后的物理机制, 利用Babushkin 等提出的解析方法[18],从微观的角度分析这种调谐太赫兹辐射产生的原因.在该方法中,太赫兹辐射是由气体电离过程中所有离散的电离事件总和贡献而成, 这种电离事件一般只发生在激光场峰值附近,相邻的电离事件彼此分离,并且每一个电离事件都具有自己独特的振幅δρn和形状H n(t),因此最终电子密度ρ(t)是在整个阿秒级电离过程中逐渐增加的, 可以看作是所有离散电离事件的总和,由式(10)表达
式(10)中:H(t−tn)为Heaviside 阶跃函数.电流的离散总和可由式(11)计算
经过傅里叶变换后的太赫兹频谱表达式
式(12)中:Cn为第n 次电离事件时的阿秒电离的振幅和电离形状
从式子(13)可以看到太赫兹的频谱是由每一个离散电离事件的总和贡献而成.因此进一步计算了电子密度随时间的增长率 ∂Ne(t)/∂t.如图5 所示,实线对应标准倍频的双色圆偏振激光,虚线对应中心频率经过调谐后的双色圆偏振激光,从图中可以看到标准倍频情形下电离事件成对出现,并且展示出相似的电离强度,因此在相关叠加的过程中,高频部分的太赫兹频谱将会相干相消.而对于二次谐波中心频率经过调谐后的双色激光场,相邻电离事件的增长有明显的差异,一个被抑制,而另一个有明显的增益,电离的增长率出现明显的三峰的结构.这一变化,将进一步决定了电离事件的数目,以及电离事件强度的相干特性,最后能够影响太赫兹辐射的频谱,以及影响在二维方向上的太赫兹波的强度,将最终改变太赫兹辐射的偏振.
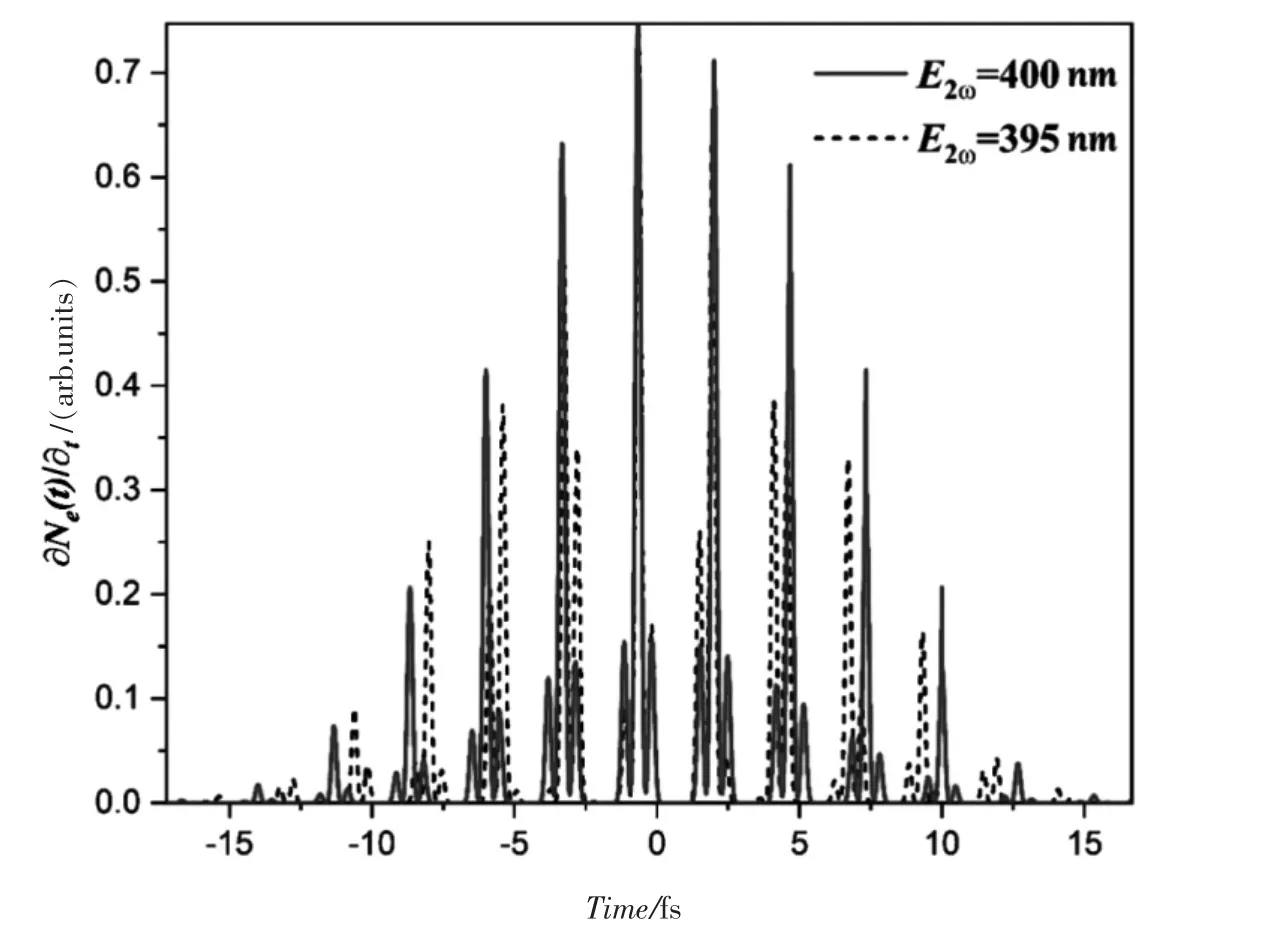
图5 不同二次谐波波长下的电子密度增长率Fig.5 The increasing rate of the electron density for the standard and tuned second harmonic two-color circularly polarized laser pulse
3 小结
基于二维光电流模型,通过数值模拟和理论分析,研究了相同螺旋性圆偏振双色激光场(CP-S)对太赫兹辐射的影响.通过对双色场中二次谐波(SW)中心频率进行调谐,低频部分的太赫兹辐射强度降低,高频部分的太赫兹辐射出现在频谱中,太赫兹的能量保持基本不变.此外,随着调谐波长的改变,太赫兹辐射的偏振特性能够从近似的线偏振到圆偏振改变.理论分析表明,太赫兹辐射频谱和偏振变化,依赖于同旋圆偏振双色场引起的电离事件相干强度的变化.研究结论将有助于人们认识圆偏振调谐的激光场对太赫兹辐射的影响.
