降雨数据时空精度对城市暴雨变异性及频率分析的影响

庄琦 刘曙光 周正正

摘要：提升城市暴雨内涝防治精细化水平是解决城市洪涝问题的关键。采用16种不同时空分辨率的降雨产品，利用暴雨时空异质性评估指标和随机暴雨移置法，在上海地区定量评估降雨数据精度对暴雨事件时空变异性诊断和频率分析的影响。研究发现利用低精度降雨数据得到的年最大暴雨序列发生时间延迟、降水量低估，暴雨过程不均匀性提升、空间不均匀性降低;在不同重现期下，降雨数据精度对频率分析结果影响有显著差异，重现期越大，低精度数据带来的低估程度越大;时间精度的影响占主导地位，可达空间精度的5倍。在城市暴雨洪涝研究中有必要采用更高精度的降雨数据，建议与研究区域类似的小型城市地区在防洪设计中使用精度达（12 h、0.05°）或以上的降雨数据。

关键词：城市极端降雨;时空分辨率;不确定性;频率分析;IDF曲线;上海

中图分类号：TV122

文献标志码：A

文章编号：1001-6791（2023）03-0398-11

收稿日期：2023-01-29;

网络出版日期：2023-04-19

网络出版地址：https：∥kns.cnki.net/kcms/detail/32.1309.P.20230418.1444.002.html

基金项目：国家自然科学基金资助项目（42271031;51909191）

作者简介：庄琦（1997—），女，江苏徐州人，博士研究生，主要从事城市水文、极端水文气象事件等方面的研究。

E-mail：2110026@tongji.edu.cn

通信作者：周正正，E-mail：19058@tongji.edu.cn

在气候变暖及快速城市化的双重影响下，近年来中国地区性暴雨落区多与城市密集区重叠，城市防洪形势复杂严峻。极端暴雨事件在时间和空间尺度上的变异性［1］及频率变化显著［2］，加之城市化流域面积相对较小、水文响应时间较快，城市洪涝管理精细化程度不高、设计标准不足等问题日益突显［3-5］。2019年发表在Water Resources Research上的研究强调了城市水文学面临数据精度不足带来的挑战［6］。为匹配城市社会经济发展的需求、满足新阶段水利高质量发展要求，在城市地区亟待使用时空精度与发展目标相适配的观测数据来提升精细化城市水灾防御能力。

降雨數据的时空精度（时空分辨率）很大程度上决定了对一场暴雨时空变异性的表达程度及频率分析的可靠程度［6］。国内外研究普遍发现使用精细时间分辨率的降雨数据能显著提高洪水模拟效果［7-8］，而粗糙时间分辨率的降雨数据会造成暴雨量级（如最大雨强、累积雨量等）被低估，且暴雨过程（雨型）不准确，从而带来洪涝风险评估的偏差［9-10］。刘业森等［11］发现随着降雨数据空间分辨率降低，暴雨空间分布被坦化、洪峰计算误差随之增加；而Ochoa-rodriguez等［12］发现降雨时间分辨率对洪水模拟结果的影响要超过空间分辨率，同时，随着流域面积的增加，降雨时空分辨率对计算结果的影响减弱；此外，Li等［13］发现受多重水文气候因子的影响，不同时空分辨率下的暴雨洪水模拟精度会呈现出复杂的非线性特征。可见，降雨数据分辨率对暴雨以及洪水特征的刻画有重要影响，但是两者作用并非简单的线性关系，不同地区的结论尚不统一。系统化、定量化分析不同精度降雨数据对暴雨时空变异性及设计暴雨的影响仍是亟待深入探讨的重要问题。

上海作为长三角一体化的核心城市，易受台风、暴雨、潮汐、洪水等多种灾害影响，是中国31个重点防洪城市之一。近年来，基于站点数据或单一精度卫星数据的研究已表明上海市极端暴雨事件的时空异质性变化及暴雨频率变化显著、城市洪涝灾害风险加剧［2，14-15］，但未见该地区针对降雨数据精度的影响问题进行定量化探讨。基于此，本文在上海市区，构建16种不同时空分辨率组合的降雨数据，对比分析数据精度对暴雨时空变异性特征刻画能力、暴雨强度-历时-频率（IDF，Intensity-Duration-Frequency）曲线计算的影响，以期对降雨数据精度在城市暴雨“时-空-频”多维结构中的作用形成更为客观、定量的认识，并提出与研究地区最适宜的降雨数据分辨率范围，为提升城市水旱灾害防御能力、也为提升城市气象“三精”能力提供科学依据。

1 研究区域及数据资料

为研究小型城市区域降雨数据精度的适用性，本文选取上海市行政面积最小的黄浦区为研究区域，面积约为20.52 km2。利用美国国家航空航天局开发的GPM-IMERG卫星降雨数据（Early V06B版本，时间分辨率为1 h，空间分辨率为0.1°，https：∥gpm.nasa.goc/data/directory）和47个上海市翻斗雨量计收集的逐时实测降雨数据，基于空间降尺度矫正技术获得2008—2017年上海市时空精度更高的格点降雨数据集（IMERG_CorSH，空间分辨率为0.01°，时间分辨率为1 h）作为本文的输入数据。

原IMERG数据（图1（a））与其他卫星降雨产品相比，在空间覆盖、捕获微雨和固态降水的性能上都有较大的优势，能更好地描绘降水量的空间分布，在缺资料及无资料地区具有明显优势［16］，但与实测值相比，该数据集在中国不同地区仍存在异质性的观测误差［17-18］。从雨量站点获得的实测降雨数据（站点位置见图1（b））被认为是最准确的数据源，但受限于站点数量有限且位置固定，空间分辨率的精细程度不如IMERG数据。为了融合两数据源的优势，应用经典的一元线性回归降尺度方法建立年尺度、0.1°精度下归一化植被指数（NDVI）数据和卫星降雨的线性关系，基于此关系和0.01°的NDVI数据估计年尺度、0.01°精度上降雨，采用时间分解方法分解得到小时尺度上的降雨数据，再基于地理偏差矫正技术（GDA）在小时尺度上进行降雨量级的修正，最终得到2008—2017年IMERG_CorSH数据集（图1（c））。本文所用的空间降尺度矫正详细步骤及结果合理性见文献［19］。

该数据集覆盖上海市，经验证，IMERG_CorSH与站点实测降水在年、月、日尺度上Pearson相关系数（Cc）均超过0.85（图1（d）—图1（f），EMA为平均绝对误差，ERMS为均方根误差），小时尺度上Pearson相关系数也高达0.74（图1（g））。相比于IMERG数据，IMERG_CorSH数据大大减少了统计误差，且提供了0.01°尺度上丰富的降雨信息、远高于雨量站的空间观测精度，可作为探究数据时空分辨率对城市极端暴雨的不确定性影响的重要数据基础。

2 研究方法

2.1 时空精度重构与极端暴雨事件提取

以0.01°、1 h原始精度为参考，对IMERG_CorSH降雨数据进行时间（6 h、12 h、24 h）、空间（0.02°、0.05°、0.1°）尺度上的分辨率重构，最终获得16种具有不同时空分辨率组合的降雨产品。时间尺度上（图2（a）），利用一维滚动窗口求和方法［20］将原始逐一小时降雨序列重采样至6 h、12 h及24 h。一维滚动窗口向前滚动的距离等于窗口长度，分别为6、12和24，相邻时刻滚动窗口不交叉，且时序重构过程保留原始降雨空间信息。同理，空间尺度上（图2（b）），利用二维滚动窗口求平均方法［12］将原始0.1°数据重采样至0.02°、0.05°和0.1°。二维滚动窗口向右、向下滚动距离等于滚动窗口边长，分别为2、5和10，相邻空间位置滚动窗口不交叉，空间重采样过程不改变时序信息。由于滚动窗口在时序上累加、空间上求平均此类采样过程并不损失或增加降雨信息，故时空分辨率重构过程不改变同场降雨的累积总雨量、面平均雨量，以此消除数据处理中的不确定性。本文使用的16种不同时空分辨率的组合见图2（c）。

基于不同时空分辨率的降雨数据提取年最大24 h降雨事件（2008—2017年）作为极端暴雨进行分析。目前针对年最大值序列的采样方法仍存在较大差异，国内一般采用正点统计法，选取当日08：00至次日08：00为1 d降雨的起止时间。而实际上，自然降雨事件中强降水过程存在跨时、跨日的现象，正点统计采样可能导致完整的強降水过程被分割、降雨累积量被低估［21］。因此，本文利用自然降水过程统计方法对年最大24 h事件进行采样，即基于24 h为滑动窗口大小、数据时间分辨率大小为滑动步长，以保留更贴近真实的降雨起止过程，并讨论时空分辨率在极端暴雨分析计算中的不确定性影响。

2.2 暴雨时空变异性特征分析

本文选取了一系列暴雨特征指标来表征暴雨事件的时空结构，包括累积暴雨量（R）、暴雨量极值（M）、暴雨变异系数（Cv）、暴雨覆盖率（F）。其中，暴雨总量是计算研究区域内t h降雨累积量，暴雨量极值、暴雨变异系数、暴雨覆盖率分别可以在时间、空间2个尺度上进行计算，计算公式见表1。

2.3 暴雨频率分析及其不确定性

随机暴雨移置（Stochastic Storm Transposition，SST）法是一种基于区域性概率重采样与地理移置相结合的地区性降雨频率分析方法。该方法利用与目标区域气候特征相同、降雨过程相似的邻域暴雨模拟延长本地样本序列，仅10 a历史数据即可获得可靠的频率分析结果［22］。SST方法结合不同分辨率降雨数据能够提供考虑降雨时空结构、数据分辨率不确定性区间的暴雨频率分析结果。此处对基于SST法的暴雨频率分析及其结果的不确定性量化作简要概括：

（1） 首先确定一个包括研究地区A流域在内、与研究区域具有相似气候特征的暴雨移置区A′。本文所选取的研究地区、移置区范围与文献［15］一致，研究地区A与移置区A′位置可参照该文献中的图1，移置区选择及结果合理性见文献［14-15］。

（2） 从n年（如本文n=10，2008—2017年）降雨序列中筛选出发生在移置区A′内、历时为Tr（本文取1、6、12、24 h）的最大的m场（本文m=200）暴雨，作为暴雨目录。

（3） 从暴雨目录中随机选择k场暴雨事件，即假设一年内发生的暴雨事件数量为k。k服从泊松分布，分布的平均发生率为λ=m/n。

（4） 对选定的k个暴雨事件进行整体移动，计算目标流域A内降雨历时为Tr的降雨累积量，并保留其中的最大值作为该年的年最大降水量。不同于传统方法，由于移置过程保留整个降雨场的时空信息，故该方法计算过程中考虑了尺度相关的暴雨时空分布结构对暴雨频率分析的影响。重复该过程N次，即可构建长为N年、历时为Tr的年最大序列。

（5） 对N年、历时为Tr的年最大暴雨从大到小排序，进行频率分析，得到IDF曲线。

（6） 本文以输入1 h、0.01°分辨率数据的频率分析结果为参考，选取相对误差（E）和时空不确定性系数（U）2个指标量化数据分辨率对频率分析结果的不确定性影响：

式中：qp，ref和qp，st分别为重现期p下利用分辨率为（1 h、0.01°）和（t h、s°）的数据所计算的IDF结果;qp，ref_0.95、qp，st_0.95，qp，ref_0.05、qp，st_0.05分别为各自对应IDF曲线上95%与5%分位数处的值，mm。

3 结果与分析

3.1 基于不同时空精度的暴雨事件提取

基于16种不同时空精度数据所提取的年最大24 h暴雨序列在发生时间和量级上存在较为显著的差异。在本节暴雨事件对比过程中，根据不同精度暴雨事件与（1 h、0.01°）事件的发生时间差异划分3种情况：若两者时间差为0 h则视作无相位差的同场暴雨事件;若两者存在时间差且时间差<24 h视作有相位差的同场暴雨事件;若两者存在时间差且时间差>24 h则视为非同场暴雨事件。

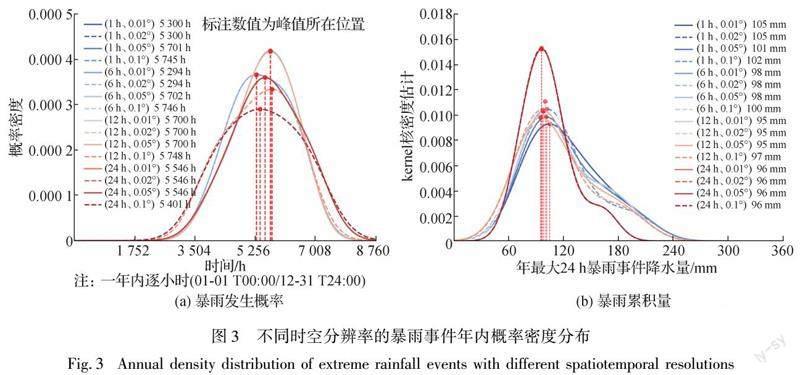
首先在发生时间上，其余15种分辨率的暴雨序列与（1 h、0.01°）结果相比，同场暴雨事件、有相位差的同场暴雨事件和非同场暴雨事件3种情况占比约为17%、70%和13%。各精度下暴雨事件的划分结果列于表2（因以（1 h、0.01°）精度为参考，故表中仅列出15种精度结果）。如（1 h、0.02°）精度下所提取的事件与（1 h、0.01°）精度下无差异;（6 h、0.01°）与（6 h、0.02°）精度下10 a均为同场暴雨但普遍存在1～5 h相位差;12 h精度下相位差进一步增加到1～17 h，并伴随1～2 a非同场暴雨;至（24 h、0.01°）～（24 h、0.05°）精度下10 a间有20%场非同场暴雨，（24 h、0.1°）精度下则有30%非同场暴雨。由表2可见，随着降雨时空精度降低，同场暴雨事件发生起止时间差异越大，且非同场暴雨事件出现的概率越大。此外，表2中69.5%的有相位差暴雨事件起始时间后置于（1 h、0.01°）暴雨。尽管各精度下暴雨发生概率最大的时间均集中在7月中下旬（峰值位置发生时间标注于图3（a）），但随着时空分辨率的降低，暴雨发生最大概率时间后移4～19 d左右，说明低分辨率捕捉的暴雨发生时间有日尺度上的滞后。

降雨量级分布上（图3（b）），随着时空分辨率的降低，雨量概率密度曲线尾部变薄、变短，而峰值处概率变高、分布更为集中，尾部风险被低估。图3（b）中，随着时空分辨率变低，雨量概率密度曲线的峰现位置前移，即年最大24 h量级被低估2.9%～9.5%;同时峰值处概率密度提高5.5%～65%，即最大24 h雨量分布更为“尖瘦”。峰值处概率变高伴随着尾部变短、极值雨量漏估，尤其是累积雨量超过130 mm的暴雨事件在粗糙分辨率下被严重低估，累积雨量超过180 mm的暴雨在不同分辨率组合下被低估4%（出现在（6 h、0.01°）处）～60%（出现在（24 h、0.05°）及（24 h、0.1°）处），累积雨量220 mm以上的暴雨在（24 h、0.1°）精度下完全被忽略。与（1 h、0.01°）相比，低分辨率数据提取的非同场暴雨事件占比变多、相位差变大造成了年最大24 h累积雨量的低估甚至漏估。

非同场暴雨事件显然会在降水量计算中带来显著差异，而即便是存在相位差的同场暴雨事件，降雨过程被粗糙分辨率分割带来的影响也不容忽视。如2013年，时间分辨率为24 h时，与1 h精度下事件相位差仅差15 h，降水量级差异为72.4 mm;2017年时间相位差仅差7 h，降水量级差异为47.5 mm，说明暴雨事件在此时极可能存在跨时、跨日的情况。使用粗糙的数据采样会将一个真实的强降水过程分割成2个（或多个）时间步长，导致低分辨率条件下提取的暴雨事件出现时间偏移、降水量被低估的情况。

3.2 时空精度对刻画暴雨时空变异性特征的影响

图4展示了基于16种不同时空精度数据所提取的年最大24 h暴雨事件的时空特征变化。本节采用相对误差（见式（1），原公式中qp，ref为参照值，qp，st为其他精度条件下的输入值）评估不同精度条件下暴雨事件时空特征指标结果的差异：如图4中以（1 h、0.01°）精度暴雨事件计算得到的时空特征指标值作为参照值，再输入其他精度下暴雨时空特征指标值计算得到量化时空精度影响的相对误差（Est）;以（1 h、s°）（s取值分别为0.01、0.02、0.05、0.1）精度下的结果作为参照值计算不同空间尺度下量化时间精度影响的相对误差（Es）;同理以（t h、0.01°）（t取值分别为1、6、12、24）精度下的结果作为参照值计算不同时间尺度下量化空间精度影响的相对误差（Et）。

从降水总量上看，随着时空精度的降低，降水总量也随之降低，如图4（a），在空间上，精度从0.01°到0.1°，相对误差Es为-2.2%;在时间上，从1 h到24 h，相对误差Et为-14.8%;最大误差出现在（24 h、0.1°）精度下，时空相对误差Est为-16%。暴雨量级的低估性在粗糙分辨率下（0.05～0.1°，12～24 h）更為显著。

在其他时空特征上，不同特征指标受时间、空间精度的影响存在差异。如图4（b）、图4（d）和图4（g）所示，随时空精度降低，暴雨量的空间极值（Ms）、空间变异系数（Cvs）和暴雨时间覆盖率（Ft）呈现单调递减趋势。数据精度由（0.01°、1 h）到（0.1°、24 h），Ms、Cvs、Ft相对误差Est分别为-29.6%、-9.1%、-24.4%，即低时空分辨率将造成Ms、Cvs、Ft的严重低估。从空间精度变化上看，精度从0.01°到0.02°，各项指标未受空间分辨率影响，Ms、Cvs、Ft在0.01°～0.02°处Es值相同。而空间精度从0.02°到0.05°，下降梯度最大，Ms、Cvs、Ft在0.02°～0.05°处Es分别下降14.3%、9%、4%。从时间精度变化上看，精度从6 h到12 h，变化梯度最大，Ms、Cvs、Ft在6 h～12 h处Et分别下降15.2%、9.1%、7.5%。可见，时间精度降低同样会影响对空间特征指标Ms、Cvs的描述，粗糙的时间分辨率亦无法合理刻画空间极值和空间不均匀性。

与Ms、Cvs恰恰相反，随着时空精度降低，暴雨量时序极值（Mt）、时间变异系数（Cvt）呈现单调递增趋势。如图4（c）和图4（e），数据时空精度由（0.01°、1 h）降低到（0.1°、24 h）将造成Mt、Cvt分别被高估22%、24.4%。空间精度从0.01°到0.02°，Mt、Cvt在各时间分辨率下相对误差值Es不变；空间精度从0.02°到0.1°，Mt、Cvt指标随着时间分辨率降低而增加。与Ms、Cvs相同，Mt、Cvt指标亦在0.02°～0.05°、6～12 h处变化梯度最为显著，Mt、Cvt在0.02°～0.05°处相对误差Es升高17.7%、14%，在6～12 h处相对误差Et升高17.6%、12.1%。可见，粗糙精度的降雨数据会导致瞬时、局地暴雨极值量级被错误估计甚至遗漏。粗糙的时间分辨率影响空间局地暴雨极值量级，同样的，粗糙的空间分辨率也会影响短历时暴雨极值量级的估计。

降雨数据时空精度对暴雨空间覆盖率（Fs）的影响更为复杂，表现为Fs随时空精度降低呈小幅波动下降趋势（Est=-2.5%，见图4（f））。Fs指标在1～6 h、12～24 h时间精度下随空间分辨率降低分别下降0.9%、0.5%，在6～12 h分辨率下又随空间分辨率降低小幅上升3.9%。空间分辨率对Fs指标的影响表现为随空间分辨率降低波动上升1.4%，但在0.01°～0.02°处Es值未见变化。说明时空精度对暴雨空间覆盖率的影响呈现复杂的非线性关系。

从影响程度上看，时间精度對暴雨时空变异性的影响强于空间精度。如对时序特征指标降雨总量（R）和Ft，时间精度约为空间精度影响的6倍；而对空间极值指标Ms，影响差异为2倍;对Mt、Fs、Cvs指标，时间、空间精度影响作用相当;对于Cvt而言，则以空间精度影响为主导。可见，时间和空间精度变化均对捕捉暴雨时空结构特征有不可忽视的影响。从指标类型上看，时间精度会影响空间指标，而空间指标也受时间精度的影响，尤其是在精细分辨率下影响更为显著。

综上，粗糙时空精度的降雨数据会低估降水总量，倾向于捕捉时序不均匀性高、空间不均匀性低的暴雨事件。采用0.02°、6 h精度以内的数据对暴雨时空特征的刻画结果较为可靠。由于实际降雨过程具有随机性，不同降雨的雨型、时段雨强、持续时间等不同，因此，用精度粗糙的数据在描述降雨时空变化特征中不充分性、不确定性应被重视。同时，降水量级、时空结构特征在数据时空精度影响下的变化及其变化程度各有不同，采用不同分辨率计算的设计暴雨不确定性有待进一步研究。

3.3 时空精度对暴雨频率的不确定性影响

将16种具有不同时空分辨率的降雨数据输入SST模型，计算得到2～200 a重现期下历时为24 h的IDF曲线，并将结果与（1 h、0.01°）分辨率下求得的IDF结果对比（图5（a））。相较于更精细的降雨数据，不同分辨率组合下的IDF结果具有不同程度的低估（E，见式（1））。6 h、12 h、24 h数据对IDF的低估率平均值分别为3%、7%和14%，0.02°、0.05°、0.1°对IDF的低估率分别为0.4%、4%和10%。时间尺度上，24 h分辨率数据最大会造成设计值低估36%，使用6 h以内分辨率的数据可以将误差控制在-0.4%～-4%之间。空间尺度上，0.1°分辨率的数据相较于0.01°的数据而言，误差在-31%～2%;使用0.05°精度内的数据进行频率分析，所得结果误差范围为-0.3%～-17%;0.02°与0.01°数据所得的暴雨事件本身差异较小，故此处设计暴雨随机误差仅有-1%～1%。

图5（a）中所展示的设计暴雨量级差异存在2个来源，一为数据时空精度误差，二为SST模拟不同降雨过程本身带来的随机误差（由于随机降雨场时空结构的变化），故图5（c）进一步剥离了不同重现期下降雨数据时空精度对IDF的影响，可见时空分辨率对IDF造成的不确定性占比接近50%，随着重现期增大（2～50 a），时空分辨率造成的低估程度增加。50～200 a重现期，受限于时序短（10 a）、以及降雨事件本身的随机成分大，随机不确定性比重亦增大，分辨率不确定性占比略降低。

可见，使用粗糙的降雨数据进行频率计算会造成设计暴雨量级的低估，且数据分辨率越低，量级低估程度越严重，随着重现期增大，时空分辨率导致的IDF不确定性亦增大。其中，时间分辨率的影响大约是空间分辨率的5倍左右（图5（b）和图5（d）），即时间分辨率的影响在该地区的极端暴雨时-空-频特征分析中占主导地位。

图6为不同重现期下使用不同时空分辨率降雨数据进行计算的设计暴雨值与（1 h、0.01°）计算结果的相对误差散点图。时间、空间分辨率均粗糙的情况下（24 h、0.1°），结果误差最大，如T=200 a时，误差达到-30%。而时间、空间分辨率中有一者较为精细时可降低结果的误差程度，如（1 h、0.1°）的数据所得结果的相对误差为-5%、（24 h、0.01°）结果的相对误差为-20%。图6中，精度在（12 h、0.05°）以内所得结果的相对误差存在一个较为平稳的平台面（T≤2 a除外），可以认为该精度内设计结果差异不显著。尽管采用（0.02°、6 h）精度以内的数据对暴雨时空特征的刻画更为准确，但频率分析时，降雨量级、时空结构特征在数据时空精度变化下的影响相互交错且复杂，最终导致精度在（12 h、0.05°）以内的频率分析结果相对误差均较小。

综上，以面积为20.52 km2的典型城市地区黄浦区为例，建议水利工程设计中（T≥2 a）使用精度在（12 h、0.05°）以内的降雨数据进行极端暴雨事件的频率计算，排水工程设计中（T≤2 a）应使用精度更高的数据为宜。

4 结 论

本文基于16种不同时空分辨率的降雨数据，利用暴雨时空异质性评估指标和随机暴雨移置法在上海市黄浦区分析了降雨数据精度对城市暴雨时空变异性特征刻画、暴雨IDF曲线计算的影响。主要结论如下：

（1） 粗糙分辨率降雨数据会造成年最大暴雨序列的抽样存在误差，主要体现在暴雨发生时间出现误差（延迟）、降水量低估、暴雨过程在时序上的不均匀性增大、空间上的不均匀程度减小。在研究区域采用（0.02°、6 h）精度及以上的数据对暴雨时空变异性的刻画结果较为可靠。

（2） 降雨数据时间和空间分辨率的影响差异较大，时间分辨率对暴雨时空变异性刻画能力的影响强于空间分辨率。数据的时间分辨率不仅会影响暴雨的时序特征，也会影响暴雨事件的空间变化特征，同理数据空间分辨率亦会对暴雨事件的时序变化特征带来影响。

（3） 降雨数据分辨率越低、重现期越大，暴雨频率结果的低估程度越大。时间分辨率影响占主导作用，大约是空间分辨率的5倍。建议小型城市地区在水利工程设计中使用时间分辨率为12 h、空间分辨率为0.05°或更高精度的输入数据。

參考文献：

［1］ZHUANG Q，LIU S G，ZHOU Z Z.Spatial heterogeneity analysis of short-duration extreme rainfall events in megacities in China［J］.Water，2020，12（12）：3364.

［2］ZHUANG Q，ZHOU Z Z，LIU S G，et al.Bivariate rainfall frequency analysis in an urban watershed：combining copula theory with stochastic storm transposition［J］.Journal of Hydrology，2022，615：128648.

［3］张建云，王银堂，贺瑞敏，等.中国城市洪涝问题及成因分析［J］.水科学进展，2016，27（4）：485-491.（ZHANG J Y，WANG Y T，HE R M，et al.Analysis of urban flooding in China and its causes［J］.Advances in Water Science，2016，27（4）：485-491.（in Chinese））

［4］徐宗学，陈浩，任梅芳，等.中国城市洪涝致灾机理与风险评估研究进展［J］.水科学进展，2020，31（5）：713-724.（XU Z X，CHEN H，REN M F，et al.Progress on disaster mechanism and risk assessment of urban flood/waterlogging disasters in China［J］.Advances in Water Science，2020，31（5）：713-724.（in Chinese））

［5］王强，许有鹏，于志慧，等.快速城市化地区多尺度水文观测试验与暴雨洪水响应机理分析［J］.水科学进展，2022，33（5）：743-753.（WANG Q，XU Y P，YU Z H，et al.Multi-scale hydrological experimental observations and responding mechanisms of storm floods in rapid urbanization areas［J］.Advances in Water Science，2022，33（5）：743-753.（in Chinese））

［6］OCHOA-RODRIGUEZ S，WANG L P，WILLEMS P，et al.A review of radar-rain gauge data merging methods and their potential for urban hydrological applications［J］.Water Resources Research，2019，55（8）：6356-6391.

［7］HUANG Y C，BRDOSSY A，ZHANG K.Sensitivity of hydrological models to temporal and spatial resolutions of rainfall data［J］.Hydrology and Earth System Sciences，2019，23（6）：2647-2663.

［8］鲁洋，涂俊，高震国，等.降雨时间分辨率对SWAT水文模拟的影响［J］.中国环境科学，2020，40（12）：5383-5390.（LU Y，TU J，GAO Z G，et al.Impact of temporal rainfall resolution on SWAT hydrological simulation［J］.China Environmental Science，2020，40（12）：5383-5390.（in Chinese））

［9］GARIANO S L，MELILLO M，PERUCCACCI S，et al.How much does the rainfall temporal resolution affect rainfall thresholds for landslide triggering？［J］.Natural Hazards，2020，100（2）：655-670.

［10］THORNDAHL S，EINFALT T，WILLEMS P，et al.Weather radar rainfall data in urban hydrology［J］.Hydrology and Earth System Sciences，2017，21（3）：1359-1380.

［11］刘业森，刘媛媛，李敏，等.降雨数据空间分辨率在城市流域洪峰变化分析中的影响［J］.地球信息科学学报，2022，24（7）：1326-1336.（LIU Y S，LIU Y Y，LI M，et al.Influence of spatial resolution of rainfall data on analysis of flood peak change in urban watershed［J］.Journal of Geo-Information Science，2022，24（7）：1326-1336.（in Chinese））

［12］OCHOA-RODRIGUEZ S，WANG L P，GIRES A，et al.Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modelling outputs：a multi-catchment investigation［J］.Journal of Hydrology，2015，531：389-407.

［13］LI X T，WANG L Z，ZHOU H L，et al.The compound effect of spatial and temporal resolutions on the accuracy of urban flood simulation［J］.Computational Intelligence and Neuroscience，2022，2022：3436634.

［14］周正正，劉曙光，WRIGHT D B.基于随机暴雨移置方法的城市设计暴雨分析［J］.水科学进展，2020，31（4）：583-591.（ZHOU Z Z，LIU S G，WRIGHT D B.Analysis of urban design storm based on stochastic storm transposition［J］.Advances in Water Science，2020，31（4）：583-591.（in Chinese））

［15］庄琦，刘曙光，周正正.上海城区降雨时空分布变化与暴雨频率分析［J］.水文，2021，41（4）：74-80.（ZHUANG Q，LIU S G，ZHOU Z Z.The change of spatio-temporal precipitation and rainfall frequency analysis in Shanghai［J］.Journal of China Hydrology，2021，41（4）：74-80.（in Chinese））

［16］熊立华，刘成凯，陈石磊，等.遥感降水资料后处理研究综述［J］.水科学进展，2021，32（4）：627-637.（XIONG L H，LIU C K，CHEN S L，et al.Review of post-processing research for remote-sensing precipitation products［J］.Advances in Water Science，2021，32（4）：627-637.（in Chinese））

［17］李麒崙，张万昌，易路，等.GPM与TRMM降水数据在中国大陆的精度评估与对比［J］.水科学进展，2018，29（3）：303-313.（LI Q L，ZHANG W C，YI L，et al.Accuracy evaluation and comparison of GPM and TRMM precipitation product over China′s Mainland［J］.Advances in Water Science，2018，29（3）：303-313.（in Chinese））

［18］胡庆芳，张野，李伶杰，等.GPM近实时反演数据对河南省2021年“7·20”极端暴雨的比较分析［J］.水科学进展，2022，33（4）：567-580.（HU Q F，ZHANG Y，LI L J，et al.Comparative evaluation of GPM near-real-time precipitation products during the 20 July 2021 extreme rainfall event in Henan Province［J］.Advances in Water Science，2022，33（4）：567-580.（in Chinese））

［19］ZHUANG Q，ZHOU Z Z，LIU S G，et al.The evaluation and downscaling-calibration of IMERG precipitation products at sub-daily scales over a metropolitan region［J］.Journal of Flood Risk Management，2023：e12902.

［20］STRAATEN C，WHAN K，COUMOU D，et al.The influence of aggregation and statistical post-processing on the subseasonal predictability of European temperatures［J］.Quarterly Journal of the Royal Meteorological Society，2020，146（731）：2654-2670.

［21］HNILICA J，SLMOV R，PEK V，et al.Precipitation extremes derived from temporally aggregated time series and the efficiency of their correction［J］.Hydrological Sciences Journal，2021，66（15）：2249-2257.

［22］WRIGHT D B，YU G，ENGLAND J F.Six decades of rainfall and flood frequency analysis using stochastic storm transposition：review，progress，and prospects［J］.Journal of Hydrology，2020，585：124816.

Abstract：Improving the accuracy and refinement level of urban flood management is the key to solving the urban flooding.The purpose of this paper is to quantitatively assess the role of rainfall resolution in detecting rainfall variability and performing rainfall frequency analyses （RFA）.A total of 16 rainfall products with a variety of space-time resolutions were used to obtain RFA results in Shanghai，China.Results are based on diagnostic indicators of rainfall variability and the stochastic storm transposition method.The results indicate that storm magnitudes are underestimated when coarse space-time resolutions are used.Furthermore，the use of low-resolution data results in a lagged estimation of storm occurrence and an under-and overestimation of rainfall variations.Depending on the return period，the rainfall resolution has a significant impact on the RFA outputs：coarser data resolution and longer return periods tend to underestimate the intensity-duration-frequency curves.It is also evident that temporal resolution has a greater impact than spatial resolution，as it accounts for five times as much of the effect.These results emphasize the importance of high-resolution rainfall data for the analysis of extreme rainfall intensities，particularly in relation to urban flooding.For flood control design purposes in urban areas，we recommend using rainfall data with a resolution of 12 h and 0.05° or finer.

Key words：urban extreme rainfall;spatiotemporal resolution;uncertainty;frequency analysis;IDF curve;Shanghai