基于大气偏振模式对称性的定向算法
2023-08-12何晓峰周文舟胡小平
黄 靖, 范 晨, 何晓峰, 周文舟, 胡小平
(国防科技大学智能科学学院, 长沙 410073)
0 引言
仿生偏振光导航能够提供长时间、高精度的航向信息, 可以与各类导航方法形成组合导航系统, 因此具有广阔的应用前景[1-3]。 目前, 偏振光定向技术正朝着工程实用化的方向发展, 三维姿态下的偏振光定向算法研究具有重要意义。
瑞士的Wehner 教授[4]基于Rayleigh 散射定律建立了一种标准大气偏振模型, 为仿生偏振光定向提供了理论基础。 Dupeyroux 等[5]利用六足机器人的里程信息结合偏振光罗盘进行了户外环境实验, 结果表明该六足机器人能够模仿沙漠蚂蚁的导航机理完成自主导航任务。 赵成帅等[6]使用连续旋转法提取偏振角图像对称轴, 提升了太阳子午线的提取精度。 张然等[7]通过改进深度神经网络对偏振图像进行云分割, 为复杂天气下的偏振光定向提供了新的思路。 使用天空偏振光进行定向的方法主要可分为两大类, 即基于几何关系的偏振光定向方法[8]与基于大气偏振模式对称性的定向方法[6,9]。 相较于第一类方法, 基于对称性的方法核心在于如何进行高精度的图像特征提取, 只要大气偏振模式的对称性存在就能实现定向, 因此具有更好的环境适应性。 从目前现有文献来看, 基于大气偏振模式对称性的定向方法只适用于偏振光测量系统水平放置时, 并未考虑倾斜姿态下的对称轴提取和航向解算。 然而大多数载体运动时通常具有一定的水平角, 从而使该方法在实际运用时具有较大的局限性。
针对这一问题, 本文研究了偏振光传感器非水平姿态下的大气偏振模式建模表征方法, 使得测量坐标系下的偏振模式对称性始终存在。 同时,本文提出了一种基于大气偏振模式对称性的载体航向角计算方法, 通过偏振模式对称轴提取实现了任意姿态下的偏振光定向。
1 三维运动中的大气偏振模式建模方法
自然光在进入大气层时受到粒子散射从而发生偏振, 在时间与位置已知的前提下, 可以通过一阶Rayleigh 散射特性来建立这一偏振模式。 大气偏振模式是关于太阳子午线呈对称分布的, 利用这一点可以提取大气偏振模式的对称轴, 从而获取太阳方位以实现定向[10]。
当偏振光传感器水平放置时, 传感器坐标系下的大气偏振模式如图1(a)所示。 偏振片的光轴指向天顶Z,S点为太阳在天球上的位置, 此时天球上的弧线SZ为太阳子午线, 大气偏振模式关于面OSZ(图1 中绿色平面)对称。 这种对称分布只与太阳位置有关, 而不依赖于偏振光传感器所在坐标系。 当偏振光传感器倾斜时, 观测区域不再位于天顶, 而是会随着水平角发生偏移。 若采用传统的建模方法, 当观测区域偏离天顶时, 测量的偏振信息将不再具有对称性。 为了使传感器在载体三维运动时仍能观测到具有对称特征的大气偏振模式, 将偏振光传感器光轴方向所对应的天空观测点Z'视为伪天顶点, 倾斜姿态下传感器坐标系的大气偏振模式如图1(b) 所示, 此时传感器坐标系下的大气偏振模式关于面OSZ'对称分布。
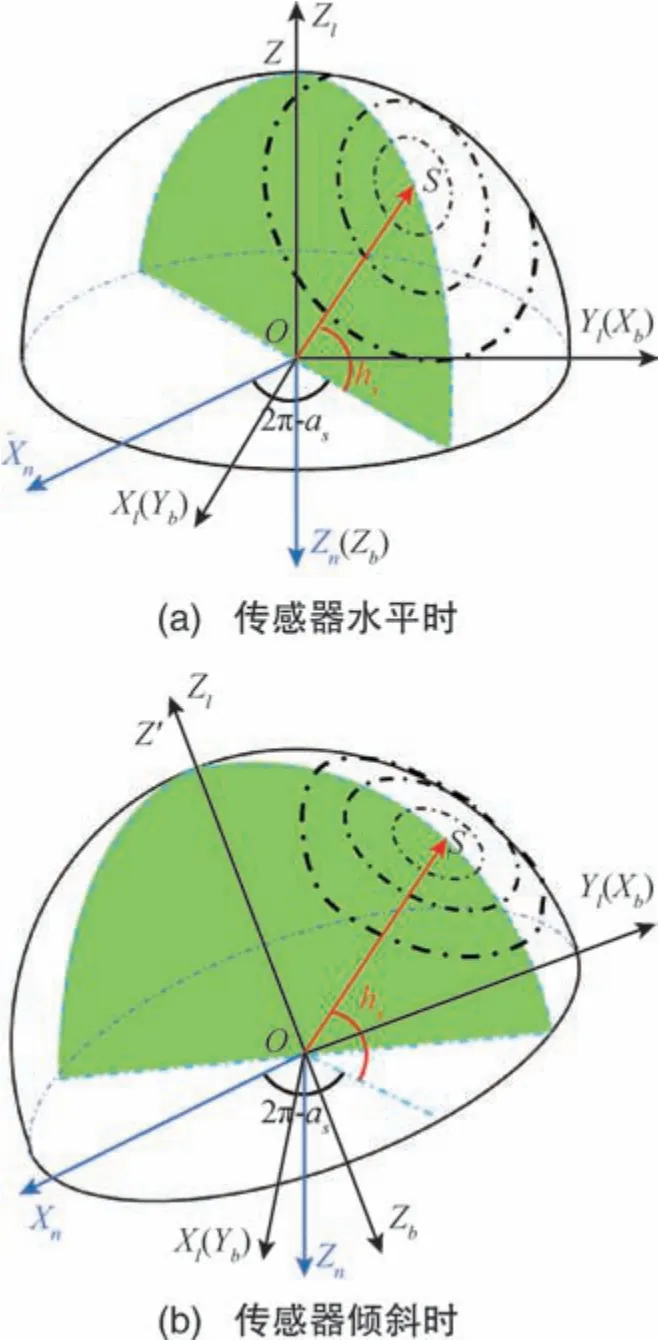
图1 传感器不同姿态时的大气偏振模式Fig.1 Schematic diagram of atmospheric polarization modes at different sensor attitudes
约定北-东-地地理坐标系为导航系(n系)、前-右-下坐标系为载体坐标系(b系)、右-前-上坐标系为传感器坐标系(l系), 三组坐标系的关系如图1所示,n系呈右手直角坐标系, 为保证图像的简洁性, 将Yn轴省略。
由天文学知识可知, 太阳方向矢量的单位矢量在系中的投影为
式(1)中,as为太阳方位角,hs为太阳高度角,两者仅与时间、地理位置有关。
假设偏振光传感器与载体固联安装,Xb轴与Yl轴重合,Yb轴与Xl轴重合,Zb轴与Zl轴成相反方向, 则从b系至l系的姿态转移矩阵为
式(4)中,φ、θ、ψ分别为载体的滚动角、俯仰角和偏航角。 载体的滚动角与俯仰角通常可由微惯性器件测量得到, 航向角为需要求解的变量。
整理式(1) ~式(4)可求得太阳方向矢量在传感器坐标系下的投影, 则可求得E矢量方向在传感器坐标系下的投影
式(5)中,OP为观测方向的单位矢量,OS为太阳方向矢量在传感器坐标系下的投影坐标。
通过坐标系变换可求得入射光坐标系i系下的E矢量方向为
则偏振角∠AOP为
式(8)中,ei(j)为E矢量方向中的第j个元素(j=1, 2, 3)。
则散射光的偏振度为
式(9)中,θ为散射角, 对应观测矢量OP和太阳方向矢量OS形成的夹角。
因此, 有
至此, 可求得任意姿态下的理论偏振角与偏振度分布。
2 基于大气偏振模式对称性的航向角计算方法
通过第1 节的建模方法, 使得大气偏振模式在测量坐标系下始终具有稳定的对称特征分布。 因此, 对测量得到的偏振信息进行适当的处理, 提取其中的太阳子午线就能实现定向。
2.1 基于梯度计算与定点约束下直线拟合的对称线提取
在实际测量中发现偏振角特性比偏振度分布更加稳定, 故使用偏振角分布进行对称轴提取。偏振角关于太阳子午线和反太阳子午线的投影呈反对称, 对称线上的偏振角大小为90°, 且对称线两边符号相反, 因此对称轴上具有最大偏振角梯度。
对偏振角图像进行梯度提取, 首先使用Sobel滤波核进行X方向、Y方向的梯度提取, 最后合成得到各像素点的梯度矢量。 在得到偏振角图像梯度值后, 选取偏振角梯度大于阈值的点作为特征点, 基于最小二乘法进行直线拟合即为偏振角图像对称轴。
运用最小二乘法拟合太阳子午线投影直线y=kx+b, 此时有
式(11) 中, (xi,yi) 为所提取特征点在传感器坐标系平面的坐标。
对于经过校正的偏振光传感器, 传感器光轴经过图像中心, 而传感器光轴指向大气偏振模式的天顶位置, 则太阳子午线投影也经过图像中心。因此, 将直线过图像中心点作为约束, 即b=0 代入式(11)可得到
图2(a)为实测偏振角信息的梯度分布, 梯度较大区域与测量偏振角对称轴基本吻合; 选取偏振角梯度大于阈值的点基于最小二乘法进行直线拟合, 同时将直线过图像中心点作为约束, 对称轴拟合结果如图2(b)所示。
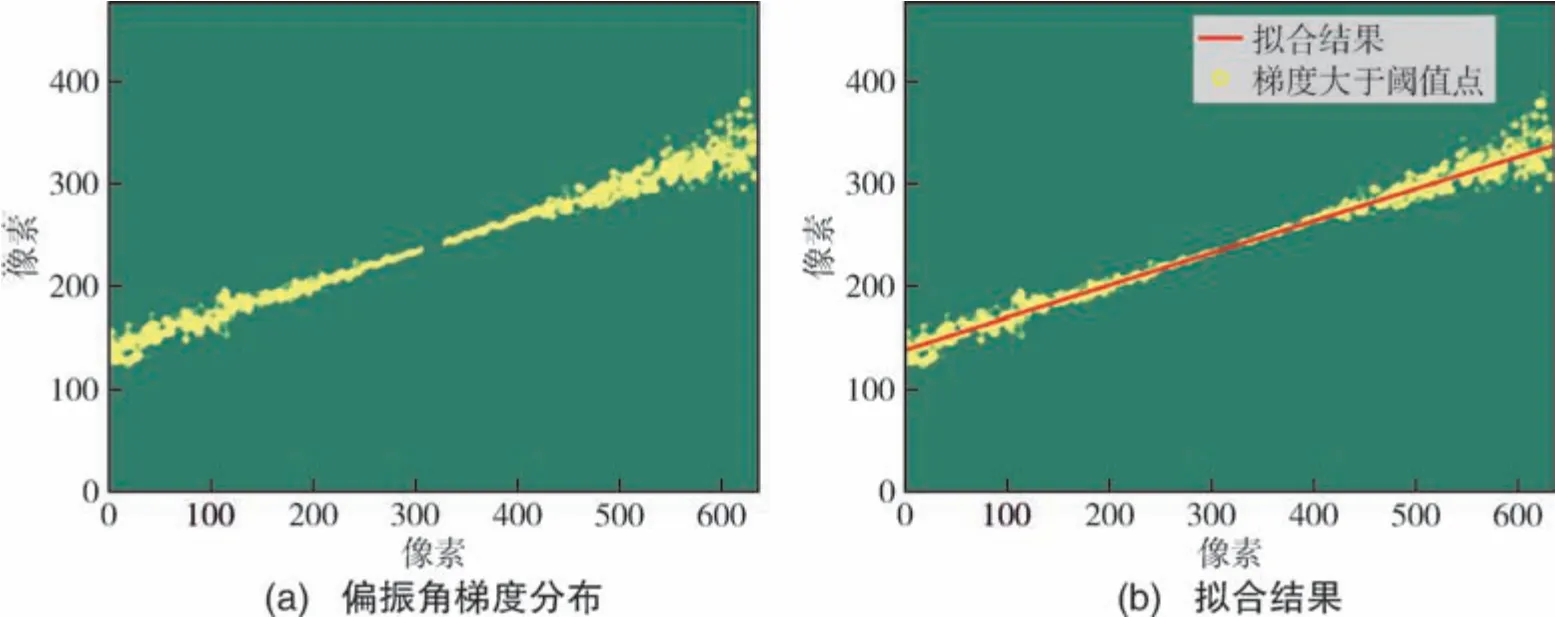
图2 偏振角梯度分布与对称轴拟合结果Fig.2 Gradient distribution of polarization angle and the fitting results of symmetry axis
进一步可以求得太阳子午线投影与传感器坐标系Xl轴的夹角
2.2 偏振光/微惯性组合定向解算
太阳方向矢量在传感器坐标系下的坐标与太阳子午线投影的关系为
式(15)中,ks1、ks2、ks3为中间变量。
求解式(15)可得到
式(16)中,as为太阳方位角, 由时间与当地地理位置求得,。
在航向计算结果存在模糊解的情况下, 该模糊解来源于计算反三角函数时所引入的模糊解。 当载体的滚动角与俯仰角为0°时, 有ks3=0、φs=0°,此时模糊解为180°, 则航向解算结果可简化为
通过给定载体初始航向并假设载体航向角缓慢连续变化, 从而求解模糊度。 当载体水平姿态角较小时, 定向模糊度约为180°。 若载体航向角缓慢连续变化, 则相邻两次航向角解算结果不超过90°, 模糊度解算流程如图3 所示。

图3 模糊度解算流程图Fig.3 Flowchart of ambiguity solution
3 实验测试
3.1 单轴转动实验
2021 年10 月20 日16 时, 在国防科技大学校内进行转动实验, 将实验装置置于楼顶开阔地带,天气晴朗。 将偏振光传感器安装在高精度单轴转台上, 以高精度单轴转台提供的转动角度作为参考值, 可以间接计算定向精度。 图4 为单轴转动实验装置图, 偏振相机采用索尼工业相机搭载IMX250MZR 图像传感器, 成像分辨率为2448(H)×2048(V), 视场角为96°。

图4 单轴转动实验装置图Fig.4 Diagram of single-axis rotation experiment device
高精度单轴转台一圈共391 格, 每旋转30 格进行一次偏振图像采集, 直至转台旋转一整周,每次转动的角度约为27.62°, 共计采样14 次。 偏振光定向的初始模糊解人为给定, 对偏振图像求取偏振角信息, 计算偏振角梯度分布, 使用定点约束加最小二乘法进行直线拟合得到对称线, 最终求取载体航向角。 航向解算过程如图5 所示,4 幅子图分别为偏振相机旋转4 次所采集得到的偏振角图像, 黄色虚线为太阳子午线拟合结果。

图5 航向解算过程示意图Fig.5 Schematic diagram of the orientation solution process
图6(a)为航向解算结果, 偏振光测量装置每旋转27.62°进行一次测量, 共旋转13 次回到初始位置。 高精度单轴转台能够提供旋转角度的参考值以间接评估定向精度, 定向误差计算表达式为

图6 转动实验定向结果Fig.6 Orientation results of rotational experiment
式(18)中, Δθ为定向结果角度差,n为旋转次数(这里为13)。 图6(b)为误差计算结果, 与目前常用的两种定向算法(LDHT 法[9]与Wang 法[11])对比, 在水平姿态下所提出的算法也具有更高的定向精度。 结果表明, 在偏振光测量装置转动一周的过程中, 均方根误差(RMSE)为0.3158°, 平均绝对值误差(MAE) 为0.2568°, 具体统计结果如表1 所示。
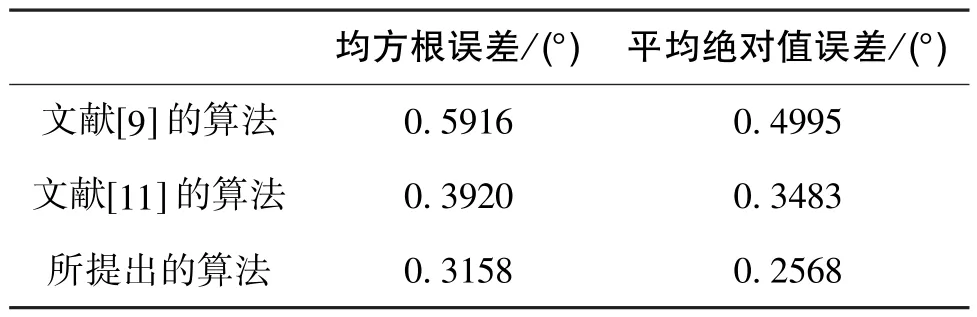
表1 单轴转动实验结果Table 1 Results of single-axis rotational experiment
3.2 倾斜姿态下的转动实验
为分析水平姿态角对定向结果的影响, 验证算法在非水平姿态下的性能, 2022 年4 月7 日10时, 在上述实验的基础上进行了载体倾斜姿态下的转动实验, 分别采用所提出的算法与简化的算法(式(18))计算倾斜时的定向误差。 图7 为倾斜姿态下的转动实验装置图。

图7 倾斜姿态下的转动实验装置图Fig.7 Diagram of rotation experiment device in inclined attitude
偏振相机参数与3.1 小节中的单轴转动实验相同, 微惯性器件采用Xsens 传感器公司的MTI-G-710 系列, 陀螺的零偏稳定性为10(°) /h, 水平姿态角零偏的均方根(RMS)为0.2°。 将偏振光传感器与可调倾角的平台固联, 平台安装在高精度电动转台上。 实验当天天气为少云, 为减小随机性误差, 电动转台每旋转30°采集两张偏振图像, 转台旋转180°后逆向旋转直至初始位置。 载体姿态为俯仰10°, 定向结果如图8 所示, 统计结果如表2所示。 由表2 可知, 当载体的水平姿态角较大时会显著影响航向解算结果。 当载体俯仰角为10°时,不考虑水平姿态角的定向误差将从1.3741°增加至5.4592°。 从误差曲线可以看出, 所提出的算法能够在载体倾斜时有效捕获大气偏振模式的对称性并实现定向解算。 随着载体航向变化, 误差曲线也随之规律性变化, 利用这一规律可以消除载体水平姿态角对定向的影响, 这也是下一步的主要工作。
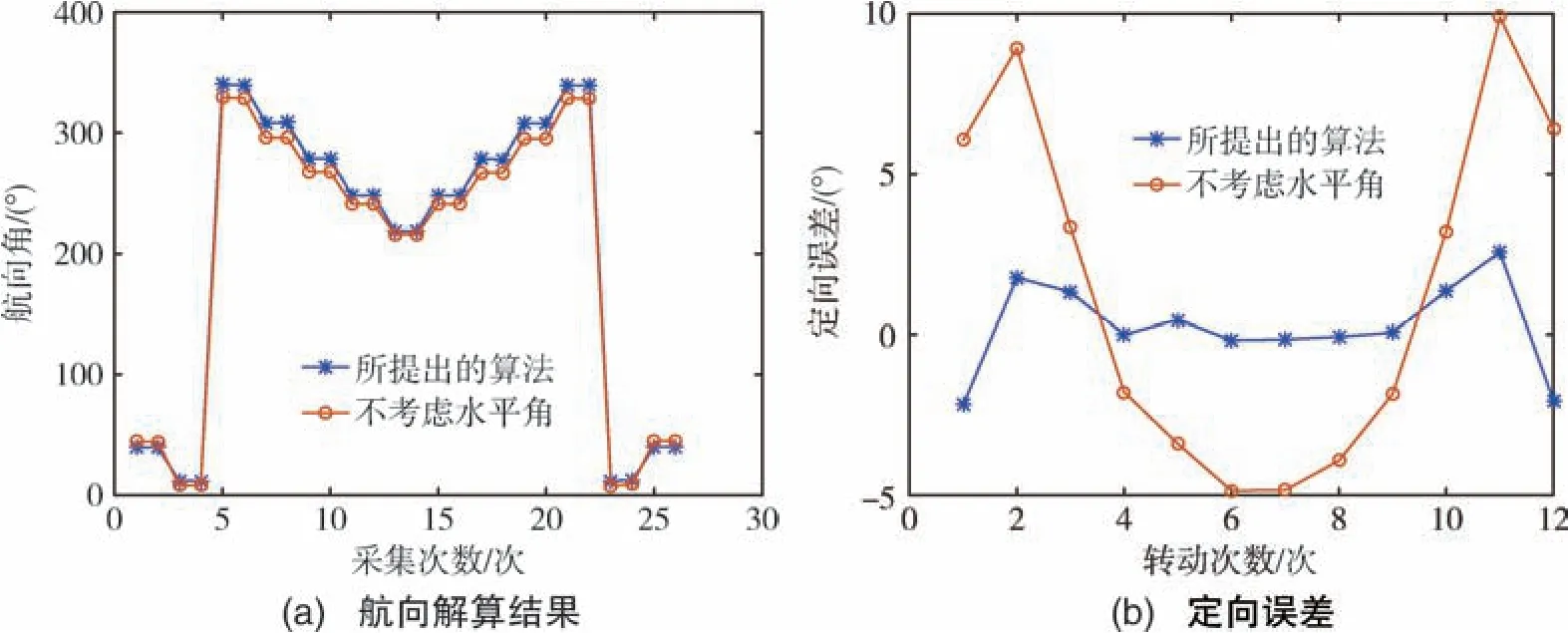
图8 转动实验定向结果对比Fig.8 Comparison of rotational experiment orientation results
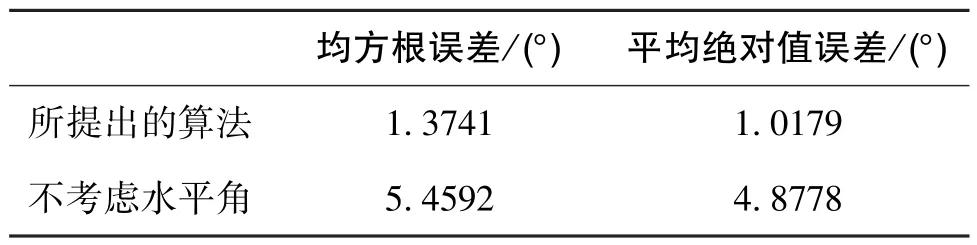
表2 倾斜姿态转动实验结果对比Table 2 Comparison of rotation experiment results in inclined attitude
4 结论
针对非水平运动条件下的偏振光定向问题,利用一阶Rayleigh 散射特性, 融合水平角信息, 提出了一种适用于载体三维运动的大气偏振模式对称定向算法。 建立了以传感器为中心的大气偏振模型, 通过姿态转换使得偏振光传感器观测区域的大气偏振模式始终存在对称性, 从而突破了对称定向算法必须保证载体处于水平姿态的限制。 采用定点约束加最小二乘法对偏振角梯度特征点进行直线拟合, 准确提取了大气偏振模式分布的对称线。融合微惯性提供的水平角信息, 建立了三维运动条件下的大气偏振模式对称定向算法。 实验结果表明,该算法能够在非水平姿态下准确定向。
