激波作用下颗粒层动态演化的双流体模拟
2023-08-12刘森胡海滨杨阳付亮亮刘晓星
*刘森 胡海滨 杨阳 付亮亮 刘晓星
(1.沈阳化工大学化学工程学院 辽宁 110142 2.中国科学院过程工程研究所多相复杂系统国家重点实验室 北京 100190 3.中国石油大学 (北京) 机械与储运工程学院 北京 102249)
在高能炸药装置中添加金属颗粒以改进或控制其毁伤性能是相关领域的研究热点之一[1-2]。当爆炸发生后,金属颗粒在高压爆炸气相产物的冲击夹带下高速抛洒,并与爆炸产物和氧气发生化学反应释放热量,以实现对目标物的毁伤。已有研究表明,冲击波作用下固体颗粒的抛洒并不是均匀的,而是首先在固体颗粒物料层表面形成射流,在爆炸气相产物的作用下射流不断向外抛洒颗粒,最终形成远场颗粒云。因此,爆炸初期固体颗粒物料层表面颗粒射流的形成及发展得到了学者的极大关注。
实验上,爆炸初期固体颗粒的射流问题一般是通过高速成像技术结合粒子回收的方式加以研究,高速成像能够得到爆炸火球外缘颗粒射流状态,而粒子回收能够得到颗粒的抛洒距离。张传山等[3]试验采用球形TNT为中心爆源,发现球形玻璃珠构成的颗粒和球壳中发生破碎的颗粒体积分数随当量比的增加呈现指数的衰减规律。蒋治海等[4]对炸药爆炸驱动不同壁厚抛撒装置的壳体变形、裂纹产生液体射流形成及其发展过程进行了试验研究,他们利用扫描电镜对破片断面进行分析发现破片的形成主要由剪切断裂造成。薛琨等[5-6]通过高速分幅照相技术研究了不同硅油含量的石英砂壳层在爆炸冲击作用下的动态抛洒过程,探究了颗粒射流的形成条件和结构特征,发现硅油含量对于固体颗粒射流的形成和发展有着重要的影响。
受检测手段以及实验本身安全性的限制,爆炸抛洒实验所能测得的信息有限。因此诸多学者采用数值模拟策略来解析爆炸冲击作用下颗粒层的射流抛洒细节。所用到的数值模拟方法可大致分为基于欧拉-欧拉策略的双流体模型和基于欧拉-拉格朗日的颗粒轨道模型。由于爆炸抛洒过程中会形成冲击波,流场中局部速度梯度极大,进而对数值求解提出了一定的挑战。本论文工作的主要目的是测试计算流体力学开源软件OpenFOAM自带的双流体模型在模拟预测冲击作用下颗粒层抛洒特性的准确性。鉴于此,本文工作针对Theofanous等[7]的冲击抛洒实验,开展了对应的双流体模拟,并定量对比了数值模拟结果和实验结果,以为后续系统研究冲击作用下颗粒物料的流动传递反应特性奠定基础。
1.数值模拟方法和参数设置
本文相关数值模拟都是基于计算流体力学开源软件OpenFOAM中的双流体模型,所用到的求解器为基于blastFOAM的blastEulerFoam。此求解器是blastFoam的欧拉-欧拉模型求解器变体,且与OpenFOAM的标准求解器相比,主要优势是可以求解任何数量的颗粒相。在双流体框架下气两相的质量、动量和能量守恒方程文献中有诸多描述,在此不再赘述。
为了检验OpenFOAM中的双流体模型能否成功模拟冲击情况的气固两相流,本论文工作中双流体模拟的主要参数设置参照试验中参数设置,如图1所示。高压气体由左侧向右冲击颗粒床层,在颗粒床层左右两侧设置两个压力监测点(-0.732m,0.1m),(0.608m,0.1m),以检测冲击波扫过颗粒床层后的气相压力变化。模拟中气体和颗粒属性都参考实验中的设置。颗粒密度为2460kg/m3,直径为0.9mm,颗粒层固含率为0.36;左侧通入冲击波马赫数为1.66的高压气体;颗粒层右侧是常压静止气体;上下壁面设置为无滑移壁面条件。模拟中气相为理想气体。

图1 算例设置示意图
2.结果与讨论
(1)冲击波演化
图2给出了冲击过程中气体压力、气体速度和固含率随时间的演化。图2(a)和(b)中的黄色垂直虚线表示颗粒层左右自由面,箭头所指为颗粒层右侧边缘。图2(a)表明,冲击波与颗粒层相互作用后,形成反射波和透射波,如1ms时刻的压力等高图所示。1ms时刻的压力等高图表明,由于激波的压缩和反射作用,反射波的压力要明显高于初始时刻的冲击波压力,参见图中右侧的颜色等高图刻度;穿过颗粒层的透射波的压力要明显低于初始时刻冲击波压力,这是因为当颗粒层与高压气体相互作用时,曳力、压力梯度力和对流传热会导致气体失去动量和总能量,从而降低了透射波的冲击强度。随着时间的推移,反射波压力逐渐降低,而透射波压力则逐渐升高,如4ms时刻压力等高图所示。在8ms时刻,透射波已经到达计算域右侧边界,而反射波尚未到达左侧边界,说明透射波的传播速度大于反射波的传播速度。在12ms时刻,反射波已经通过左侧边界,反射波的压力进一步降低,与此同时透射波的压力进一步升高。

图2 冲击过程中(a)气体压力;(b)气体速度和(c)固含率随时间的演化
图2(b)表明,当冲击波与颗粒层界面相互作用形成反射波和透射波后,颗粒层左侧气体速度降低,而右侧气体速度升高,气体的反射速度和透射速度界面与气体压力界面保持一致。在1ms时刻,可以看到颗粒层左侧附近区域气体速度明显降低,与上游的高速气体间形成了一个明显的间断面,这是由于冲击气体撞击到颗粒层后,颗粒层对气体的反射作用,反方向传播的反射波削弱了入射波的波速;而床层右侧气体速度的增高则是由于高压气体透过颗粒床层形成透射波。与此同时,高压气体持续透过颗粒层,颗粒层右侧的气体速度持续增大,如图2(b)中4ms和8ms时刻速度等高图所示。但整体上,颗粒层右侧气体速度的增加幅度要大于颗粒层左侧气体速度的增加幅度,可以看到在4~12ms,颗粒层右侧的气体速度要高于颗粒层左侧的气体速度。
图2(c)给出了颗粒层固含率随时间的演化。初始时刻颗粒层固含率设置为0.36,由于颗粒层的膨胀,局部最大固含率在4ms时刻降低到0.1。为了更好地展示固含率沿冲击方向的变化,图2(c)中的右侧图例最大固含率设置为0.1。随着时间的演化,颗粒层宽度逐渐增大,固含率逐渐降低。这是因为高速气体的夹带作用使得固体颗粒层形成沿冲击方向的运动、膨胀的趋势。
(2)模拟与实验结果对比
图3给出了颗粒床层两侧监测点处压力随时间的变化,图中的黑色曲线为实验测量得到的压力信号。为了检验计算网格对模拟结果定量准确性的影响,数值模拟中考察了三个网格尺寸:2mm、4mm、8mm,在数据处理上将冲击波前沿抵达颗粒层的时刻定义为t=0时刻。

图3 监测点P1和P2处压力随时间的变化
图3表明,模拟得到的压力信号能够在定量上与实验结果较好吻合。如图3(a)所示,对于位于颗粒层左侧的P1监测点,在冲击波前沿抵达颗粒物料层表面后反弹至P1监测点的时间间隔,实验测量结果约为2.7ms,数值模拟得到的结果为2.5ms;P1监测点处的压力随后急剧增大至一极大值,实验测量结果为6.5bar,模拟结果为6.8bar;P1监测点处的压力随后逐渐降低,实验测得的压力值呈现较明显的波动,数值模拟中因为将颗粒床层做了拟流体处理,得到的压力信号非常平缓,但压力值整体上都处于实验测得压力数据的波动范围内,参见网格尺寸为2mm和4mm的模拟结果。
图3(b)对比了P2处压力信号的实验结果和数值模拟结果。P2处压力变化大致可以分为5个阶段:在第一阶段压力维持在常压;随后压力急剧增大,表明透射的冲击波前沿抵达P2监测点,实验测得的抵达时间为1.5ms,峰值压力为1.6bar,模拟得到的抵达时间为1.5ms,峰值压力为1.5bar;在第三阶段,P2处透射波致使压力仍逐渐增大,但是增大的速率要小于第二阶段,该阶段的结束时间和对应压力,实验测量结果为3.0ms和2.3bar,数值模拟结果为3.1ms和2.3bar;第四阶段,实验结果和数值模拟结果都表明P2处压力近似保持不变,这主要是透射波和接触波已经通过P2处,然而颗粒层仍未到达P2位置;在第五阶段,P2处压力逐渐增大,这主要是因为该阶段固相颗粒已抛洒至P2位置,P2位置始终处于颗粒云内部,由于颗粒运动而产生的压缩波使压力逐渐增加。
试验中通过对颗粒层动态演化高速摄像图片的数值处理追踪了冲击波扫过之后,颗粒床层左右表面位置的时间演化。图4对比了模拟预测结果和实验结果,监测点位于y=0.1m。在高速气体的冲击压缩和夹带作用下,颗粒层呈现整体向右移动的趋势;颗粒层左侧表面处物料同时受到气体向右的冲击夹带作用和向左的固体应力阻碍作用,而颗粒层右侧表面与常压气体毗邻,所受阻力较小,这使得颗粒层右侧表面的运动速度要明显大于颗粒层左侧表面的运动速度,即颗粒层整体上呈现向右膨胀的变化趋势。由图4看到模拟预测结果能够与实验测量结果很好的定量吻合,再次说明本论文工作数值模拟结果的定性和定量可靠性。
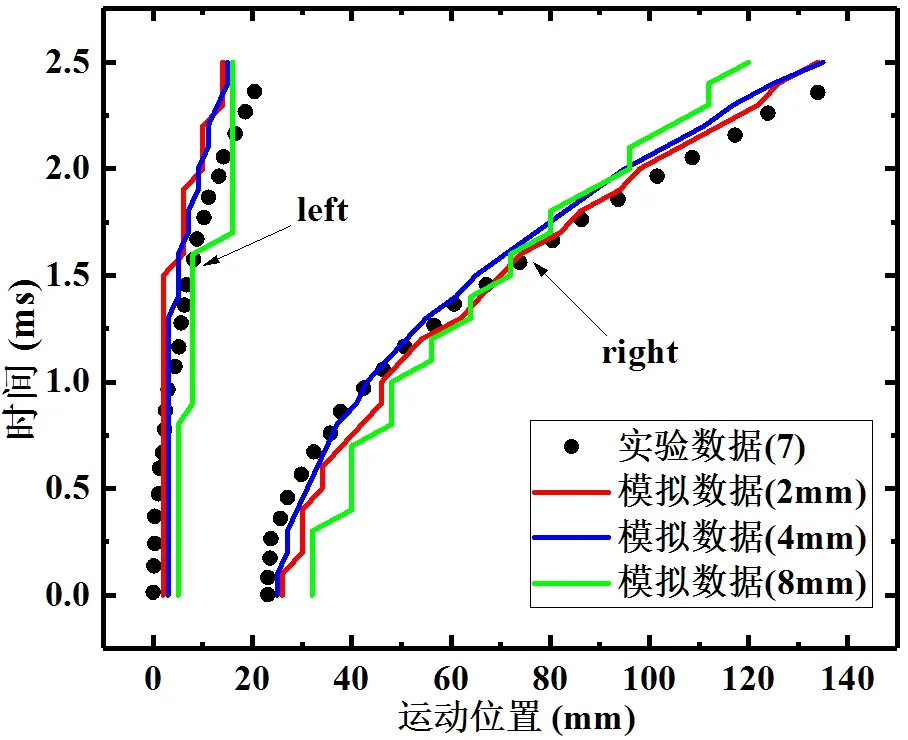
图4 颗粒层左右两侧位置随时间的变化趋势验证
3.结论
本文工作采用计算流体力学软件OpenFOAM自带的双流体模型及相应求解器,模拟高压高速气体与悬浮颗粒层之间的流体力学作用,主要研究结果如下:
(1)当高压高速气体抵达悬浮颗粒层时,会形成反射波和透射波;反射波的逆向传播使得颗粒层上游气相压力先急剧增大,而后逐渐减小;透射波的传播使得颗粒层下游压力逐渐上升;冲击过程中气相夹带作用使得颗粒层沿冲击方向飘移,且颗粒层逐渐膨胀。
(2)模拟预测的颗粒层上游和下游检测点处的气相压力变化,以及颗粒层左右界面位置的时间演化,都能与实验结果很好的定量吻合,说明OpenFOAM中的双流体模型和相应求解器能够模拟预测冲击条件下的气固流体力学作用。
