探索教学新路径 提高学生思考力

王素沙

【摘 要】课程内容的呈现方式直接影响学生对学习内容的感知与理解。数学新课标强调对内容进行结构化整合，将具有一致学科本质特征的内容整合为一个主题，帮助学生整体理解和把握课程内容。本文以“数与运算”和“图形的认识与测量”两个主题的相关内容为例，探讨应如何通过内容的整体分析和教学设计，使学生掌握核心概念，促进学生对学习内容的理解和迁移，提高学生的思考力，发展学生的核心素养。

【关键词】数与运算 图形的认识与测量 学科本质 数学思考力

课程内容的呈现方式直接影响学生对学习内容的感知与理解。《义务教育数学课程标准（2022年版）》强调对内容进行结构化整合，将具有一致学科本质特征的内容整合为一个主题，可以帮助学生整体理解和把握课程内容。

一、数与运算

数学新课标中数与代数领域，将原来的数的认识和数的运算整合为数与运算，更好地体现了数的认识与运算的联系，有助于学生从整体上理解、掌握数与运算的本质和关键内容，也有助于学生全面地思考问题，提高学生的思考力。

数是运算的基础，运算是数的应用。数是基于计数单位的表达，运算是寻求计数单位及其计数单位的个数，它们都基于计数单位。在数的认识方面，整数、小数和分数的认识都可以看成计数单位的“累积”。在数的运算方面，整数、小数和分数的加减法，无论是整数的末尾对齐、小数的小数点对齐，还是分数的通分，都是将相同计数单位的个数进行加减。难点在于乘除法的一致性。

（一）乘法教学一致性

整数乘法和分数乘法都是根据乘法的意义进行教学的，但小数乘法是根据积的变化规律进行教学的。教材是按照先学习整数乘法，再学习小数乘法，最后学习分数乘法的顺序编排的。在根据积的变化规律进行小数乘法的教学时，学生较难理解“越乘越小”的问题，解答这个困惑仍需借助小数乘法的意义。因此，教师不妨尝试根据小数乘法的意义进行小数乘法的教学。

利用小数乘法的意义教学小数乘法离不开计数单位乘计数单位，为了让学生更好地理解0.1×0.1=0.01，教师除了借助数位顺序表、方格图等，在教学整数乘法时也可以让学生学习计数单位乘计数单位。因此，学习乘法的整体思路应该是“乘法意义—表内乘法—10×10，10×100等计数单位乘计数单位—整十数乘整十数或整百数—多位数乘一位数—两位数乘两位数—三位数乘两位数—小数乘整数—小数计数单位乘小数计数单位—其他小数乘法—分数乘整数—分数单位乘分数单位—真分数乘真分数—假分数乘假分数—整数、小数、分数乘法的联系”。

这样重新规划教学路径，学生才能在整数乘法中打好基础；在学习小数乘法后找到思考方向；在学习分数乘法时能乐于思考、自主规划学习方向，提高思考力，培养迁移能力，在整体回顾比较整数、小数、分数乘法的过程中思考乘法运算的本质，把握数学核心概念。

（二）除法教学一致性

目前整数除法和小数除法都是一个计数单位一个计数单位地分，当计数单位不够分时细分计数单位后继续分，但分数除法则是根据逆运算——除以一个数等于乘这个数的倒数来教学的，学生理解起来有困难。为了实现除法教学的一致性，在教学分数除法时，教师不妨仍然细分计数单位。例如， ÷4= ÷4=， ÷= ÷ =14÷15=。通过这样一致性的教学路径，相信学生一定能根据学习整数和分数的除法的经验基础，进行一致性的思考，合理进行方法的迁移。

（三）沟通四则运算

小学阶段数的运算主要是四则运算，从运算的本质来说，加法是所有运算的基础，一切运算都可以从加法推演出来。数的运算最早是从数的累加开始的，加法运算与自然数的产生是同步的。自然数从1开始，在后面不断累加“1”，就产生更大的数。用这样的方式表示更大的数的时候，就出现了进位制，如大部分都是十进制。减法是加法的逆运算，与自然数的产生和加法运算直接相关。乘法是加法的简便运算，本质上也是加。乘法口诀只表示加的结果，省略了加的过程。除法是乘法的逆运算。直接从乘法的本质理解除法，就是减去若干个相同的数。

四则运算是相互联系的，在学习过程中，教师可以引导学生借助实际情境，在进一步理解加、减、乘、除运算意义的基础上，沟通它们之间的联系，将所学知识形成体系，理解加、减、乘、除一致性的问题，把握学科本质。

案例一：北京版数学二年级上册“加減乘除的整理与复习”

活动一：复习加法和乘法的联系。

①芳芳用小棒搭四边形，搭了7个，一共用了多少根小棒？

加法算式：4+4+4+4+4+4+4=28

乘法算式：7×4=28 或 4×7=28 （强调乘法算式表示的意义：7个4是28）

乘法口诀：四七（二十八）

②丽丽用小棒搭七边形，搭了4个，一共用了多少根小棒？

加法算式：7+7+7+7 =28

乘法算式：7×4=28 或 4×7=28 （强调乘法算式表示的意义：4个7是28）

乘法口诀：四七（二十八）

活动二：复习减法和除法的联系。

①芳芳用28根小棒搭四边形，可以搭几个呢？（28里有几个4）

减法算式： 28-4-4-4-4-4-4-4=0（追问算式的意思）

除法算式： 28÷4=7

乘法口诀：四（七）二十八

②丽丽用28根小棒搭七边形，可以搭几个呢？（28里有几个7）

减法算式：28-7-7-7-7=0 （追问算式的意思）

除法算式：28÷7=4

乘法口诀：（四）七二十八

活动三：讨论加、减、乘、除的联系。根据乘法口诀“四七二十八”你能想到哪些算式呢？请你写一写，讲一讲算式背后的故事。

学生在讲算式背后故事的过程中，理解了加、减、乘、除之间的联系。在这部分内容中，学生容易理解的是加法和减法互为逆运算、乘法和除法互为逆运算。对于乘法是加法的简便运算学生比较有经验，但在理解除法是减法的简便运算时有困难。下面分享除法初步认识（平均分）的教学片段。

案例二：北京版数学二年级上册“除法的初步认识”（平均分）

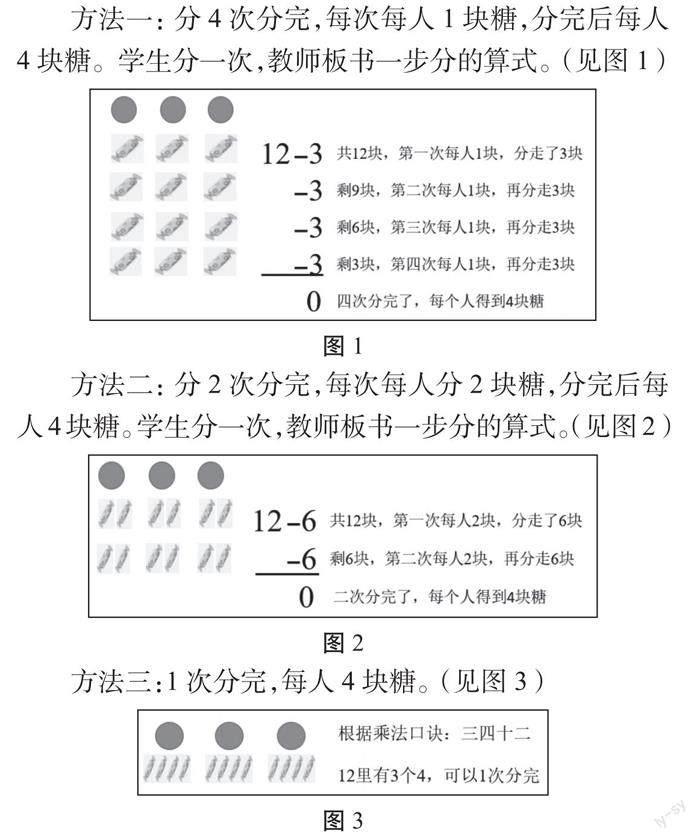
有12块糖，分给3个小朋友，要让每个小朋友分的糖一样多，请你分一分。

活动要求：（1）请你分一分；（2）要让人看出你分的过程（每一次怎么分的）。

汇报交流：

方法一：分4次分完，每次每人1块糖，分完后每人4块糖。学生分一次，教师板书一步分的算式。（见图1）

方法二：分2次分完，每次每人分2块糖，分完后每人4块糖。学生分一次，教师板书一步分的算式。（见图2）

方法三：1次分完，每人4块糖。（见图3）

在分糖的活动中，教师每一次板书减法算式，都能让学生体会到平均分与减法的联系，为学生体会除法和减法的关系做好了铺垫。

从数的运算本质思考，学生想获得数学核心知识、把握数学的本质及思想方法、提高思维能力、发展核心素养，都需要教师精心设计教学，抓住知识间的内在联系，把一个个知识点转化成知识的网络，让学生在解决问题的过程中提高思考能力。

二、图形的认识与测量

图形的認识与测量密不可分，数学新课标对图形与几何内容进行了结构化整合，将图形的认识与图形的测量整合成一项主题内容。为了帮助学生理解度量本质，培养其空间观念和推理意识，逐步形成联系地看问题的思维方式，形成结构化的思维方式，提高学生的思考力，在教学长度、面积与体积时，教师应该建立概念与度量的整体认知结构，让学生能迁移和理解它们概念本质的一致性和度量本质的一致性。

长度、面积、体积都以单位测量为核心，需要学生在经历单位的建立中形成量感。量感的培养离不开度量单位产生的必要性，离不开统一度量单位的必要性，离不开换算度量单位的必要性，离不开感知度量工具产生的误差，离不开正确估计大小。

只有在长度单位的学习中打好基础，在面积单位的学习中进一步感受度量单位产生的必要性、统一度量单位的必要性等，才能在体积单位的学习中，学会思考、学会迁移，学会用定量的方式思考和解决问题。

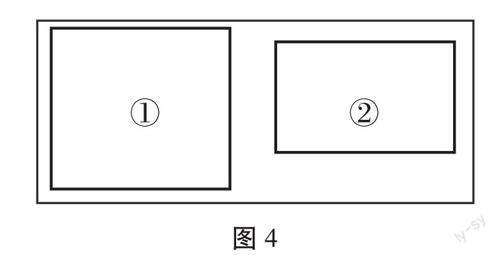
案例三：北京版数学三年级下册“面积和面积单位”

活动一：

说清楚图4中①比②大多少，在这个活动中，学生从感性认知上升到度量意识，感受产生单位的必要性。

活动二：设计不同的学具（大正方形、小正方形、圆形等）去量，选择合适的度量单位。在汇报过程中发现结果不一致，体会统一单位的必要性。

案例四：北京版数学五年级下册“体积和体积单位”

活动一：

说清楚图5中①比②大多少。在活动中感受产生单位的必要性。

活动二：设计不同的学具（大正方体、小正方体、球体等）去量，选择合适的度量单位。在汇报过程中发现结果不一致，体会统一单位的必要性。

长度、面积和体积的学习都要经历概念的建立、比较方法的运用、测量工具的选择和测量单位的产生等，这样一致性的教学更能培养学生全面地去思考问题，从而理解数学本质。

以上结合具体教学案例分析了“数与运算”和“图形的认识与测量”这两个主题的教学实施路径，这样的教学实践能促进学生掌握数学核心概念，促进学生对学习内容的理解和迁移，提高学生的思考力，发展学生的核心素养。