信息技术开启“做数学”的自我导航

金兴伟

【摘 要】数学是一门逻辑性很强的学科，抽象程度很高。运用现代化的信息技術手段，引导学生在全方位、直观、准确的学习场域中进行自我导航学习，在“做数学”的过程中，帮助学生认识数学的本质问题，使其充分感受到数学的思维性与严谨性。本文以信息化手段和“做数学”进行深度融合，为推动数学学科育人提供新型范式与有益探索。

【关键词】信息技术 “做数学” 自我导航 励课

“做数学”是以“做”为支架的一种数学学习活动，是以学生运用材料和工具，在手脑相协同的过程中人人参与的实际操作为特征的数学活动。近年来，现代化信息技术的教学专用软件平台功能逐渐多样化，实用性更强。以励课平台为例，它从形象生动的画面、“声”文并茂的演绎、动静结合的展示，为学生自主学习提供了思想的条件支持和物化的环境，能有效地帮助学生理解数学知识、解决数学问题。在这样的背景下，学生自主学习的技术含量和层次会越来越高，同时也被赋予更多的技术内涵。

以苏教版数学五年级上册“钉子板上的多边形”一课为例。这节课对学生已有的知识层次有一定的挑战，需要通过“做数学”带领学生体验观察、运算、猜想、验证等活动的过程，发现钉子板上多边形的面积和边上钉数以及形内钉数的关系。为了帮助学生开展数学活动，教师可引导学生借助励课平台和网络的支持进行自主探究学习，但在自主学习的过程中，学生会面临“我在哪里”“我下一步该到哪儿”“怎么做”“做什么”等困惑和疑问。由于学习信息量大，知识链接关系复杂，容易产生“迷路”的问题，教师可引导学生利用“寻起点—定目标—探路径—研方法—慧思路—促成长”自我导航学习模式的步骤，借助自我导航系统制订计划、设置目标，对照目标，对自己的思维、情感和行为进行调整、监测、评价和控制，从而确保学习效果和学习目标的达成。

下面详说励课平台环境下“钉子板上的多边形”一课的教学流程：

一、寻起点：问卷调查分析学情

为提高学生的自我导航学习效率，基于学生已经学过“多边形的面积”，在课前通过问卷星进行网络调查。调查内容有关于多边形面积的知识，以及对钉子板上的多边形有哪些疑惑等。既要了解数学探究规律中需要掌握哪些知识，学生是否掌握，又要及时发现学生存在的知识盲区，然后为教学设计提供强有力的依据，也为自我导航学习寻找正确的学习起点。

问卷设计：

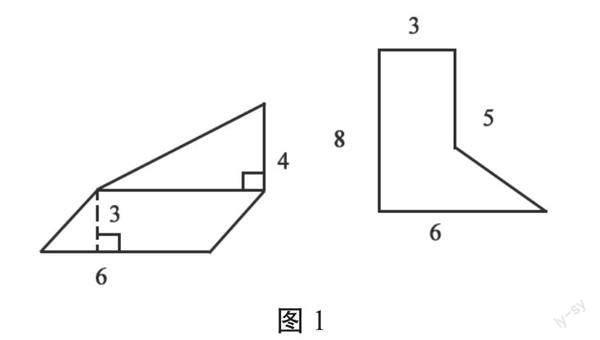
1.计算图1中图形的面积。

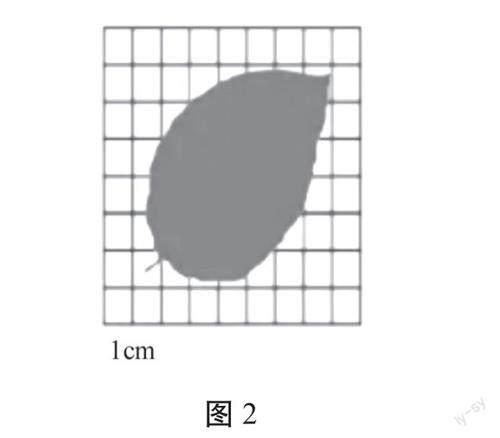
2.图2中每个小格子的面积为1平方厘米。请你估计这片树叶的面积。

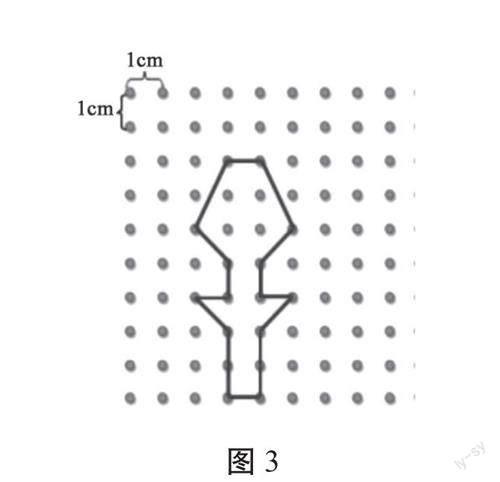
3.图3中每两点的距离为1厘米，请问：图中这个多边形的面积是多少？对这张图你有什么疑问吗？

二、定目标：创设情境发现问题

游戏导入：教师将钉子板图呈现出来，介绍学生认识钉子板，并将其抽象成一幅幅的点子图画。说明每两点的距离为1厘米，每相邻的4个点构成一个小方块，面积为1平方厘米。借助励课平台下发点子图，学生在平板上自主绘制感兴趣的多边形。

投屏展示学生的画图过程，教师可以很快说出在钉板上多边形的面积大小。常言道，好的开始是成功的一半。巧妙地导入，可以激发学生强烈的学习兴趣，激发学生强烈的参与动力，收到事半功倍的教学效果。这一导入环节引发了学生对快速求面积的好奇心，可以调动学生主动参与学习的热情，从而引导学生继续深入探究。

三、探路径：实验探究验证猜想

（一）计算感悟

探索活动一：出示例题的3个规则图形和1个不规则图形（如图4），通过励课平台下发表格，学生填写表格，要求学生计算面积并思考如何计算不规则图形的面积，再议一议面积与钉子板的联系。

（二）引发猜想

学生观察图形，在钉子板上算出多边形的面积。可以通过数格子、公式或者组合图形等方法计算面积，教师启发学生推测：多边形的面积可能跟边上的钉子数有一定的关系。让学生数出多边形边上的钉子数，找出面积与钉子数存在的规律。在线提交答案，投屏展示学生在平板上的探索过程，汇报并交流。猜想当形内钉子数是1枚的情况时，多边形面积公式是S=n÷2（n表示边上的钉子数）。

运用猜想培养学生的探究意识，并与验证相结合，鼓励引导学生大胆猜想，让学生通过主动参与学习，主动获取知识，形成一定的问题模式，从而在解题中寻找最优化的策略。

（三）验证猜想

探索活动二：举例验证探索活动一的猜想与钉子板上的所有多边形是否相符合。学生利用平板在励课平台下发的练习上任意画一个多边形，验证探索活动一得到的公式是否符合所有的多边形。教师利用同屏技术分享探究过程，练习提交后屏幕共享呈现所有可能出现的探究结果，帮助学生归纳出面积大小，不仅与边上的钉数有关，而且与内部的钉数也有一定的关系。最后得出结论：只有形内钉子数是1枚的多边形的面积才是S=n÷2，即当a=1时，S=n÷2（a表示一个形状中的钉子数）。

课堂举例是数学教学中常用的一种手段，同时也是课堂教学的一种艺术。恰当的事例，能起到催化剂的作用，对学生开阔学习思路、加快对新知识的吸收消化、提高学习兴趣、活跃课堂气氛都有很大的帮助。学生在平板点子图上任意画一个多边形进行验证，既体现了数学的严谨性，又说明了猜想所获规律的单一性。

四、研方法：运用结构深入探究

探索活动三：利用结构，探究形内钉数是多枚的情况。教师利用励课平台下发三组形内钉子数不同的图形（如图5所示），要求学生猜想出不同的公式。学生四人小组合作学习，在三组图中任意选择一组多边形，探索发现面积计算公式。其中三人每人选择同一组图中的一个，第四人负责在平板上记录相关数据，最后对数据进行分组分析，研究它们的内在规律。全班汇报交流时利用同屏技术和屏幕共享技术共享实验成果，各组自主选择，得到猜想后进行验证。

选择性学习是一种差异性的教学形式，由于学生之间存在着各方面的差异，因此这种教学形式可以成为教师因材施教，提高教学实效的手段，也是教师探索创造出的学生的数学学习方式之一，能有效发展学生的核心素养。

五、启思路：刨根问底发现本质

（一）发现本质

探索活动四：进一步验证形内钉数为多枚的情形。通过励课平台发布点子图，要求学生在点子图上验证探究活动三猜想出的公式，使其能通过多个公式寻找出其中的规律，交流形内钉子数为0的情况，最后得出皮克公式S=n÷2+（a-1）。

学生由先前选定的分组进行探索研究，提出对各组情况的猜想，对选定的分组必须再次进行例题验证，以体现数学的严谨性，突出以上规律适用于本类别的一般情况。

（二）课堂练习

巩固新知，用公式计算任意多边形的面积。学生自编习题，套用公式求出多边形的区域面积。组织学生利用公式，以两人一组的形式组成自测学习小组。学生利用平板任意绘制多边形图在组内自测，既加强了学生的自主学习能力，又激发了学生的学习兴趣。同时，重点讲解和点评学生存在的问题，及时查漏补缺。

六、促成长：回顾反思灵活运用

（一）收获与体会

引导学生结合板书回顾整节课上自主探究的学习过程，以及发现规律的一般过程，谈具体的体会和收获。结合学生的讲解，对探究中的不完全归纳法和用字母表示规律形成公式的数学思想进行总结。

（二）数学阅读

为了深度理解公式，了解数学文化，教师通过励课平台上网检索功能发送百度网址，由学生自主搜索皮克定理以及我国数学家闵嗣鹤编著的《格点和面积》一书中对皮克定理的介绍。利用信息化平台，提供课外读物，为今后学生学习数学埋下伏笔。

数学是一种文化，数学课堂作为文化教育的载体，理应生动活泼、文化韵味独特。作为传播数学文化的载体，数学课堂要致力于培养学生持久学习、探究数学的兴趣，力求让每一位学生都有丰富的数学文化素养。学生利用平板电脑寻找网络上的数学文化，所获取的知识要远远大于教师想要表达的内容。

一堂好课，就是师生共同探索数学的一次美妙之旅。在信息化支撑下的数学课堂上，教师要基于学生的需求将同伴合作运用到课堂，以学生为主体地位，积极引导学生进行自我导航学习。注重选择和重组学习资源、优化学习方法、创生多元化的评价，科学设计和实施教学过程，充分展示开放、便捷的信息技术优势，促使“做数学”在更深层次上培育学生的理性精神、创新意识与积极状态。