小题应小做 图形巧助力
2023-08-11谢盛富


在高中数学中,数形结合是数学学科中重要的数学思想,往往伴随函数与方程思想、分类讨论思想、特殊与一般思想等,与逻辑推理、数学运算、数学抽象等核心素养相交融.通过对图形的观察与分析,化抽象为直观,化直观为精确,本文以高考试题为例,仅从图形的角度浅谈它在高考小题中的巧用巧做,并列举两道方法类似的高考试题,以期抛砖引玉.
一、图形在函数中的巧用
函数是高中数学最重要的主干知识,也是解决实际生活、生产中的重要模型.初高中所学习的基本初等函数、其组合函数与复合函数,与参数的引入构成了丰富多彩的函数类型,其图象与基本性质相得益彰,图形凸显性质,性质勾勒出图形,相辅相成,尤其是在解决与抽象函数有关问题时,图形发挥出关键作用.
例1 (2020年新高考卷Ⅰ第8题,卷Ⅱ第8题)若定义在R的奇函数f(x)在(-∞,0)单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是().
A.[-1,1]∪[3,+∞)B.[-3,-1]∪[0,1]
C.[-1,0]∪[1,+∞) D.[-1,0]∪[1,3]
分析与解:本题考查函数的奇偶性、单调性以及抽象函数不等式的解法.如图1,先根据题设初步画出函数f(x)的大致图象,再向右平移1个单位长度,再结合xf(x-1)≥0可求得-1≤x≤0或1≤x≤3,故选D.
例2 (2020年北京卷第6题)已知函数f(x)=2x-x-1,则不等式f(x)>0的解集是().
A.(-1,1) [WB]B.(-∞,-1)∪(1,+∞)
C.(0,1) D.(-∞,0)∪(1,+∞)
分析与解:本题是函数与不等式的交汇,意图考查转化思想、函数思想、基本初等函数的图象与性质.先由f(x)>0得2x>x+1,转化为指数函数y=2x的图象与直线y=x+1的位置关系问题.如图2,不等式f(x)>0表示的含义是指数函数y=2x的图象在直线y=x+1的上方,因而可得x<0或x>1,故选D.
点评:在解题中,通过图形呈现出函数的性质、关键特征,能迅速求解问题,有事半功倍之效,因此,作出函数对应的大致图形是解题的关键.与例1类似题有2014年新课标卷Ⅱ理科第15题、2017年新课标卷Ⅰ理科第5题,与例2类似题有2019年天津卷文科第8题、2015年北京卷理科第7题.
二、图形在立体几何中的巧用
高考对空间立体几何的考查主要是点线面之间的位置关系、常见几何体的结构特征及其表面积与体积、空间角与距离,还有一些动态问题,主要是应用传统几何方法或建系引入空间向量来求解相关问题.对于立几问题,借助它们的几何特征进行转化,运用有关的性质定理、判定定理或结论、计算公式进行求解.
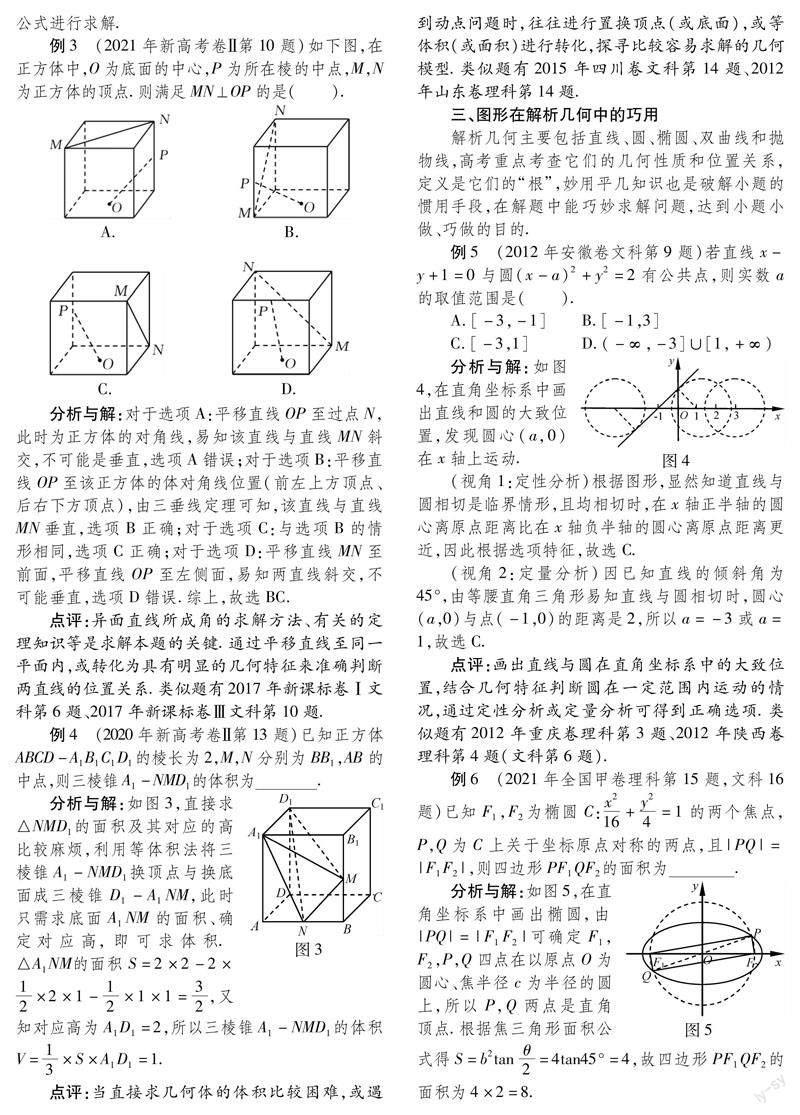
例3 (2021年新高考卷Ⅱ第10题)如下图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点.则满足MN⊥OP的是().
分析与解:对于选项A:平移直线OP至过点N,此时为正方体的对角线,易知该直线与直线MN斜交,不可能是垂直,选项A错误;对于选项B:平移直线OP至该正方体的体对角线位置(前左上方顶点、后右下方顶点),由三垂线定理可知,该直线与直线MN垂直,选项B正确;对于选项C:与选项B的情形相同,选项C正确;对于选项D:平移直线MN至前面,平移直线OP至左侧面,易知两直线斜交,不可能垂直,选项D错误.综上,故选BC.
点评:异面直线所成角的求解方法、有关的定理知识等是求解本题的关键.通过平移直线至同一平面内,或转化为具有明显的几何特征来准确判断两直线的位置关系.类似题有2017年新课标卷Ⅰ文科第6题、2017年新课标卷Ⅲ文科第10题.
例4 (2020年新高考卷Ⅱ第13题)已知正方体ABCD-A1B1C1D1的棱长为2,M,N分别为BB1,AB的中点,则三棱锥A1-NMD1的体积为_____.
分析与解:如图3,直接求△NMD1的面积及其对应的高比较麻煩,利用等体积法将三棱锥A1-NMD1换顶点与换底面成三棱锥D1-A1NM,此时只需求底面A1NM的面积、确定对应高,即可求体积.△A1NM的面积S=2×2-2×12×2×1-12×1×1=32,又知对应高为A1D1=2,所以三棱锥A1-NMD1的体积V=13×S×A1D1=1.
点评:当直接求几何体的体积比较困难,或遇到动点问题时,往往进行置换顶点(或底面),或等体积(或面积)进行转化,探寻比较容易求解的几何模型.类似题有2015年四川卷文科第14题、2012年山东卷理科第14题.
三、图形在解析几何中的巧用
解析几何主要包括直线、圆、椭圆、双曲线和抛物线,高考重点考查它们的几何性质和位置关系,定义是它们的“根”,妙用平几知识也是破解小题的惯用手段,在解题中能巧妙求解问题,达到小题小做、巧做的目的.
例5 (2012年安徽卷文科第9题)若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是().
A.[-3,-1] B.[-1,3]
C.[-3,1] D.(-∞,-3]∪[1,+∞)
分析与解:如图4,在直角坐标系中画出直线和圆的大致位置,发现圆心(a,0)在x轴上运动.
(视角1:定性分析)根据图形,显然知道直线与圆相切是临界情形,且均相切时,在x轴正半轴的圆心离原点距离比在x轴负半轴的圆心离原点距离更近,因此根据选项特征,故选C.
(视角2:定量分析)因已知直线的倾斜角为45°,由等腰直角三角形易知直线与圆相切时,圆心(a,0)与点(-1,0)的距离是2,所以a=-3或a=1,故选C.
点评:画出直线与圆在直角坐标系中的大致位置,结合几何特征判断圆在一定范围内运动的情况,通过定性分析或定量分析可得到正确选项.类似题有2012年重庆卷理科第3题、2012年陕西卷理科第4题(文科第6题).
例6 (2021年全国甲卷理科第15题,文科16题)已知F1,F2为椭圆C:x216+y24=1的两个焦点,P,Q为C上关于坐标原点对称的两点,且|PQ|=|F1F2|,则四边形PF1QF2的面积为_____.
分析与解:如图5,在直角坐标系中画出椭圆,由|PQ|=|F1F2|可确定F1,F2,P,Q四点在以原点O为圆心、焦半径c为半径的圆上,所以P,Q两点是直角顶点.根据焦三角形面积公式得S=b2tanθ2=4tan45°=4,故四边形PF1QF2的面积为4×2=8.
点评:本题抓住|PQ|=|F1F2|,利用平几知识判断出点P,Q与点F1,F2四点共圆,进而转化为圆与椭圆的相交问题,再借助焦三角形的二级结论求解.类似题有2021年新高考卷Ⅰ第14题、2020年新课标卷Ⅰ文科第11题.
四、图形在概率与统计中的巧用
几何概型、正态分布、古典概型等都有对应的图形或树状图,直方图、叶茎图和散点图等本身就是图形.这些图形有其自身特有的几何特征,在解题中充分借助特征有助于求解相关问题.
例7 (2021年新高考卷Ⅱ第6题)某物理量的测量结果服从正态分布N(10,σ2),下列结论中不正确的是().
A.σ越小,该物理量在一次测量中在(9.9,101)的概率越大
B.σ越小,该物理量在一次测量中大于10的概率为0.5
C.σ越小,该物理量在一次测量中小于9.99与大于10.01的概率相等
D.σ越小,该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等
分析与解:如图6,对于选项A:σ为数据的标准差,σ越小,数据在μ=10附近越集中,所以测量结果落在(9.9,10.1)内的概率越大,选项A正确;对于选项B:由正态分布密度曲线的对称性可知该物理量一次测量大于10的概率为0.5,选项B正确;对于选项C:由正态分布密度曲线的对称性可知该物理量一次测量结果大于10.01的概率与小于9.99的概率相等,选项C正确;对于选项D:因为该物理量一次测量结果落在(9.9,10)的概率与落在(10.2,10.3)的概率不同,所以一次测量结果落在(9.9,10.2)的概率与落在(10,10.3)的概率不同,选项D错误.综上,故选D.
点评:本题破解之道就是利用正态分布密度曲线的对称性求解,通过作出大致图象即可解决问题.类似题有2015年山东卷理科第8题、2011年湖北卷理科第5题.
例8 (2021年全国乙卷理科第8题)在区间(0,1)与(1,2)中各随机取1个数,则两数之和大于74的概率为().
A.79 B.2332 C.932 D.29
分析与解:如图7,在平面直角坐标系xOy中,不妨设x∈(0,1),y∈(1,2),则它们组成一个边长为1的正方形;而x+y>74表示的区域是在直线x+y=74的右上方,根据几何概型有P=1-12×34×341×1=2332,故选B.
点评:线性规划知识与几何概型相结合,体现知识的交汇性,通过简单地作出图象能够迅速得出它们的面积之比.类似题有2016年新课标卷Ⅰ理科第4题、2015年湖北卷理科第7题.
五、图形在平面向量中的巧用
平面向量既有大小又有方向,具有“数”和“形”的天然特征,是一座有效沟通各知识模块的“优质”桥梁,在解决很多数学问题时,可借助平面向量巧妙求解,让人耳目一新,豁然开朗.
例9 (2020年新高考卷Ⅱ第3题)在△ABC中,D是AB边上的中点,则CB=().
A.2CD-CA B.2CA-CD
C.2CD+CA D.2CA+CD
分析与解:本题考查平面向量的基本定理,会用某一组基底表示平面内的任一向量.如图8,画出△ABC,过点B分别作AC,CD的平行线,分别交直线CD,AC于点N,M.由于D是边AB的中点,所以CM=CA,CD=DN,因此CB=CM+CN=-CA+2CD,故选A.根据中位线也可写出CD=12(CA+CB),反解得CB=2CD-CA.
点评:三角形法则和平行四边形法则是向量加减运算的重要依据,命题者往往会结合等分点或角平分线等进行考查,此时,善用平几知识,结合图形能迅速求解问题.类似题有2018年新课标卷Ⅰ理科第6题(文科第7题)、2015年新课标卷Ⅰ理科第7题.
例10 (2020年新高考卷Ⅰ第7题)已知P是边长为2的正六邊形ABCDEF内的一点,则AP·AB的取值范围是().
A.(-2,6) B.(-6,2) C.(-2,4) D.(-4,6)
分析与解:本题考查平面向量的数量积运算.根据数量积的几何意义知AP·AB表示AP在AB方向上的投影与|AB|的积.如图9,点P运动到点C位置时,投影最大;点P运动到点F位置时,投影最小.计算得AC·AB=2×23×cos30°=6,AF·AB=2×2×cos(-120°)=-2,因此AP·AB∈(-2,6),故选A.
点评:求解数量积问题时,除了运用定义式a·b=|a||b|cosθ,还要注意它的几何意义和极化恒等式的应用,这可能会成为命题者反套路的一种新命题方式,因此解题时,若无法直接用定义式求解,不妨结合图形,运用数量积的几何意义进行求解.类似题有2017年北京卷文科第12题、2013年新课标卷Ⅱ理科第13题(文科第14题).
图形具有优美性、对称性、和谐性与独特性,可以直观地将问题呈现出来,有助于解决问题,但不一定能完全展示出本质特征.数学家华罗庚曾精辟论述“数缺形时少直观,形缺数时难入微”、“以形助数”、“以数助形”.数学是严谨的,图形的形状、大小及位置的判断,需要数量来弥补,数是形的抽象概括,形是数的直观表达,因此充分利用图形和具体的数量关系等求解数学问题,激发学生学数学的热情,从心理上认同、走进数学,不会害怕数学运算,提高学好数学的积极性,往往会有“柳暗花明又一村”的完美境界,体验解题成功的喜悦感和成就感.
参考文献
[1]中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[S].人民教育出版社,2020.
[2]谢盛富.善用平几知识妙解圆锥曲线问题[J].福建中学数学,2020(2):31-33.
本文系2021年新罗区教育科研重点课题“新教材背景下提高数学运算能力的策略研究”(编号:XL1452022072)的阶段性研究成果.
