2022年高考全国甲卷圆锥曲线试题探究与变式

李贤江　黄信

圆锥曲线一些解答题常常含有极点与极线的背景.极点与极线是高等几何的重要理论，是解决圆锥曲线一些复杂问题的巧妙方法.学生如果了解极点与极线理论，那么就可预知结果并且减少大量繁琐运算.

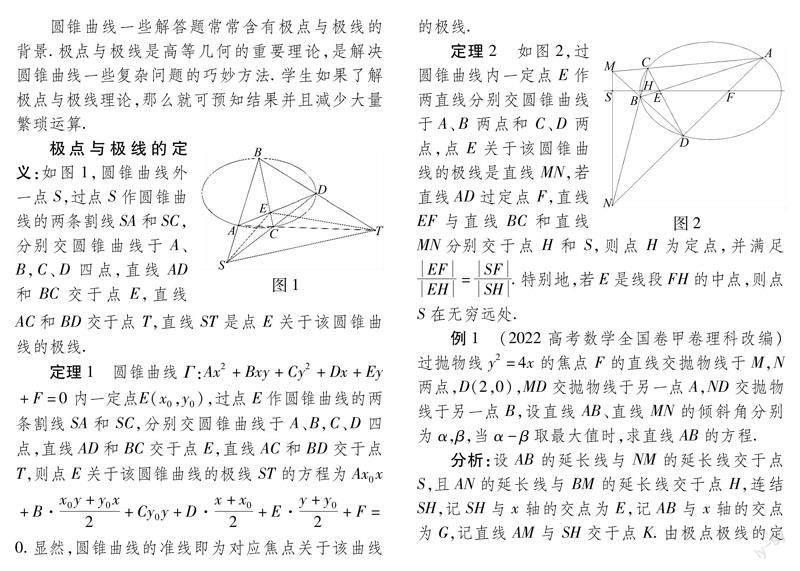
极点与极线的定义：如图1，圆锥曲线外一点S，过点S作圆锥曲线的两条割线SA和SC，分别交圆锥曲线于A、B，C、D四点，直线AD和BC交于点E，直线AC和BD交于点T，直线ST是点E关于该圆锥曲线的极线.

定理1 圆锥曲线Γ：Ax2+Bxy+Cy2+Dx+Ey+F=0内一定点E（x0，y0），过点E作圆锥曲线的两条割线SA和SC，分别交圆锥曲线于A、B，C、D四点，直线AD和BC交于点E，直线AC和BD交于点T，则点E关于该圆锥曲线的极线ST的方程为Ax0x+B·x0y+y0x2+Cy0y+D·x+x02+E·y+y02+F=0.显然，圆锥曲线的准线即为对应焦点关于该曲线的极线.

定理2 如图2，过圆锥曲线内一定点E作两直线分别交圆锥曲线于A、B两点和C、D两点，点E关于该圆锥曲线的极线是直线MN，若直线AD过定点F，直线EF与直线BC和直线MN分别交于点H和S，则点H为定点，并满足EFEH=SFSH.特别地，若E是线段FH的中点，则点S在无穷远处.

例1 （2022高考数学全国卷甲卷理科改编）过抛物线y2=4x的焦点F的直线交抛物線于M，N两点，D（2，0），MD交抛物线于另一点A，ND交抛物线于另一点B，设直线AB、直线MN的倾斜角分别为α，β，当α－β取最大值时，求直线AB的方程.

分析：设AB的延长线与NM的延长线交于点S，且AN的延长线与BM的延长线交于点H，连结SH，记SH与x轴的交点为E，记AB与x轴的交点为G，记直线AM与SH交于点K.由极点极线的定义可知，D关于该抛物线的极线是SH.再由定理1知，极线的方程是x=－2，所以E（－2，0）.由定理2知G是定点，且DGDF=EGEF.于是G的坐标为（4，0）.其次，tanα=SEEG，tanβ=SEEF，于是可知2tanα=tanβ，由S在y轴的左侧可知tanα，tanβ同号，所以，要使α－β取最大值，应使tanα，tanβ<0.