浅谈社会热点问题中的思政教育设计——以贝叶斯公式在核酸检测问题中的应用为例

王玉琢

（海军工程大学基础部数学教研室，湖北武汉 430033）

在“三全育人”的思潮背景下，全国高校都在如火如荼地开展思政教育[1]。军队是国家的拳头，思想的锈蚀比枪炮的锈蚀更可怕，因此，军校课程的思政教育承担着更特殊的责任和使命[2]。

贝叶斯公式是我校本科公共必修课程“工程数学”中的一个重要知识点，也是目前高校教师思政案例设计的热点。如陈耀庚等[3]通过介绍贝叶斯公式的诞生背景，培养学员坚持真理的精神；顾丽娟等[4]用贝叶斯公式诠释“狼来了”和“烽火戏诸侯”等古代故事蕴含的哲学思想，教导学生要诚信做人；任传荣等[5]以1968年美国天蝎号核潜艇沉没事件为背景，展示了贝叶斯公式在军事领域中的应用。然而，这些案例大多以经典的思政元素为主，展示了贝叶斯公式丰富的哲学内涵，但围绕社会热点话题的设计较少。习近平总书记指出，思政教育要有知识视野、国际视野、历史视野。社会热点问题通常反映了国内外新事物的发展变化，在网络普及、信息爆炸的时代，稍有不慎很容易触发网络舆情[6-8]。因此，结合社会热点问题来讲解科学知识，对引导青年大学生理性看待社会问题、树立正确的是非观有重要意义。

一、贝叶斯公式

假设B为某一随机事件，A1，A2，…，An是导致B发生的所有可能原因或前提条件，满足。由全概率公式可得B发生的概率为。再利用条件概率公式，可以得到

贝叶斯公式由英国数学家Thomas Bayes于1736年提出[9]。其中，称为原因Ai的先验概率，它的取值一般在试验开始之前就是已知的，由人们根据以往经验估计获得；而是当试验结果B已经发生之后，对各种“原因”发生的可能性大小的重新认识，因此称为后验概率。当我们面临不确定性的现象，需要对未知进行预测时，可以首先根据已有的信息和统计资料先给出一个先验概率，然后在新信息不断累积、不断更迭的情况下调整对未知事件的重新认识，因此，贝叶斯公式蕴含了“由果溯因”的哲学思想。

二、思政案例设计

材料1：西班牙卫生部长萨尔瓦多·伊拉2020年3月25日宣布，西班牙已从中国购买了价值4.67亿美元的医疗用品，不过随后西班牙政府宣布计划向中国退还9000套快速检测试剂盒，因为它们被认为“不合格”，但这批“不合格”的新冠病毒快速检测试剂盒是西班牙卫生部之前自行采购的。多家美国媒体依然将其列入了西班牙政府的采购清单中，并试图向外界表示，中国的新冠病毒检测试剂盒质量不高，中国还在用错误的病毒检测试剂盒误导全世界。对此，中国驻西班牙大使馆在推特上回应称：中国和中国企业的捐赠中并未包含涉事中国企业的新冠病毒核酸检测试剂盒；西班牙卫生部3月25日采购的中国医疗设备尚未离开中国，而中国商务部向西班牙提供的供应商清单中也未包括该涉事企业；这家位于中国深圳的涉事企业尚未获得中国国家药品监督管理总局销售其产品的官方许可。

材料2：2020年6月2日，湖北省政府新闻办公室召开新冠疫情防控工作新闻发布会，公布了全民核酸检测结果。这场为期10多天、耗资9亿元、覆盖近千万人的大检测，集中展现中国抗疫的重大成果，也让武汉成为外媒眼中的最安全城市。武汉市委常委、市人民政府常务副市长胡亚波介绍说，2020年4月8日，武汉实现了物理意义上的解封，集中核酸检测排查后，封城期间作出巨大牺牲的武汉人民实现了心理上的解封。核酸检测期间，卢祖洵教授团队就全民核酸检测对疫情防控及社会经济价值进行了充分论证，还承担了数据收集、资料整理和学术研究的工作，得到了政府部门的认可。“通过这次筛查，换来了全国人民的放心、武汉人民的安心，充分体现了我们党人民至上的执政理念。”

材料3：2022年6月29日国家卫生健康委员会发布了《新型冠状病毒肺炎防控方案（第九版）》，根据奥密克戎变异株的流行特点对防控措施做了进一步优化。其中对密切接触者和入境人员的核酸检测措施从“集中隔离医学观察地1，4，7，14天核酸检测，采取鼻咽拭子”调整为“集中医学观察第1，3，5，7天和居家健康监测第3天核酸检测，采集口咽拭子”。中国疾控中心传防处研究员王丽萍说：“这样的调整不会增加疫情传播的风险，是精准防控的体现”。

问题：假设根据历史资料统计显示，自然人群中感染新冠病毒的概率为0.0004。某核酸检测试剂的真阳性率（指感染新冠病毒人群中经该试剂检测后呈阳性的人数比例）为0.98，假阳性率（指未感染新冠病毒人群中经该试剂检测后呈阳性的人数比例）为0.01。现有一人核酸检测结果为阳性：

①试求此人实际感染新冠病毒的概率，并结合结果谈谈你对材料1所述问题的看法；

②结合材料2谈谈你对武汉市全民核酸这一决策的看法。

③结合材料3，请你谈谈对核酸复检的看法。

三、问题分析

记随机事件A={新冠病毒感染者}，随机事件B={核酸检测结果为阳性}。则根据已知条件，自然人感染新冠病毒的概率为P(A)=0.000 4，该核酸检测试剂的真阳性率为，假阳性率为=0.01。于是某个核酸检测呈阳性的人，实际感染新冠病毒的概率就可以用条件概率表示，且由贝叶斯公式可得

式（2）说明，一个核酸检测呈阳性的人真正感染新冠的可能性仅有3.77%。显然，这个检测的准确率是非常低的。那么是不是因为该检测试剂的质量问题才导致检测的准确率不佳呢？不妨假设经工艺和技术改良之后，该核酸试剂的真阳性率提高至0.999且假阳性率降低10倍，再次用贝叶斯公式计算，并将结果与原结果进行比较。

从表1中看出，一个使用改进试剂检测呈阳性的人，实际感染新冠病毒的可能性有28.56%。虽然相对3.77%的准确率提高了不少，但这一结果仍不尽如人意。另外，0.999真阳性率的检测剂质量已相当高，要达到这种工艺水平，实际中不仅需要耗费大量的经济成本，还需要经历大量的研发时间，根本难以应对新冠病毒的传播速度和变异速度。

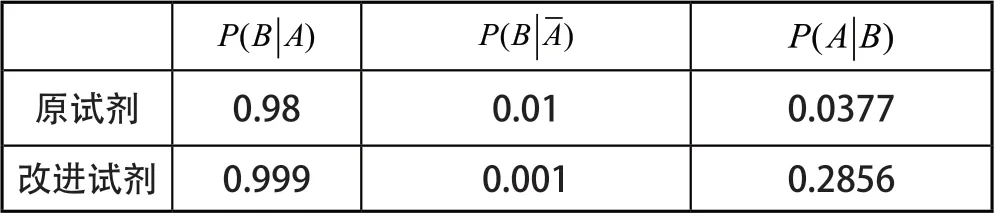
表1 两种核酸检测试剂的检测结果比较

利用贝叶斯公式进行以上分析后，我们知道，仅凭一次核酸检测呈阳性无法断定此人是否感染新冠病毒，检测试剂存在假阳性率和假阴性率是客观现象。因此，从科学的角度来看，一味追求高精度检测试剂的做法并不是行之有效的抗疫防疫方法，新冠病毒的早发现早筛查才是首要问题。在这个过程中，各国理应做好核酸检测试剂出口的质量把控，但材料1中所述的外国媒体抹黑我国合规出口的核酸检测试剂质量不合格的言论，完全是歪曲事实、不讲科学的谬论，是为了达到政治目的而混淆视听的做法。

接下来，既然核酸检测试剂必然存在假阳和假阴的情况，一次核酸检测呈阳性又无法断定此人是否感染新冠病毒，是否就没有必要采取这项医学诊断手段？我们不妨记一个核酸检测结果为阴性的人，实际感染新冠的可能性为。利用贝叶斯公式可得这个概率为

根据已知条件，一个从未做过核酸检测的自然人感染新冠病毒的可能性概率为0.000 4。而式（2）的结果表明，一个人如果做了核酸检测并呈阳性，此时虽不能断定他必然感染了新冠病毒，但他被感染的可能性从0.000 4上升到了0.037 7，几乎上升了100倍；而核酸检测如果呈阴，式（3）的结果又表明，他被感染的可疑性就从0.000 4下降到了0.000 008，下降了200倍。可见，尽管核酸检测一次阳性的确诊概率很低，但作为一种经济又便捷的手段，在新冠病毒的早期发现和排查上具有积极意义，能够快速划分疑似人群，有利于疫情的提早发现与防治，也有利于稳定民心，恢复生产。

经过上述分析，我们可以看到材料2中描述的武汉市政府采取的举措，实际上是经过了科学的分析和考量，政府办事是讲究科学的。武汉市要想经济快速复苏，武汉市民需要信心，全国各地的人民需要放心。从医学上讲全民核酸不是必要的，但是从社会学、经济学上来讲，是十分有必要的。

最后，既然核酸检测对于新冠病毒的早发现早确诊具有重要意义，而一味提高试剂工艺并不可取，那该采取何种方法发挥核酸检测的作用呢？我们注意到某人核酸检测一次呈阳性，虽然不一定就是感染者，但此人从自然人群也上升到疑似人群了，也即他感染病毒的先验概率P(A)从0.000 4更新为0.037 7。因此，再次利用贝叶斯公式，我们能够得到他第二次核酸检测为阳性的情况下可能感染病毒的可能性。不断利用计算结果更新此人感染病毒的先验概率，我们能得到此人复检多次后感染病毒的概率，如下表2。

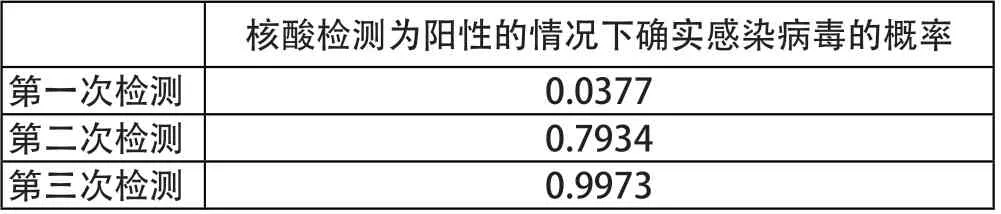
表2 核酸复检的结果比较

可以看到，在第二次检测呈阳性的情况下，此人感染病毒的可能性就为0.7934，这个值已经比较大了，可以说是高度疑似感染者。在第三次检测结果为阳性的情况下，此人感染病毒的可能性为0.9973。这个概率值可以说此人基本确诊。贝叶斯公式揭示了核酸检测多次复检的手段，本质上是通过不断地修正或者说更新先验信息，来提高推断的准确度。在临床上，医生往往都会先望闻问切，再开诊单，最后联合多种诊疗手段下结论，这些方法本质上也都运用了贝叶斯的思想。不仅如此，我们还能发现仅通过一次复检，就可以将某人阳性情况下确实感染病毒的推断的准确率从0.037 7提高到0.7934，不需要提高检测试剂的工艺。可见，贝叶斯公式中还蕴含了人力资源和优化统筹的哲学思想。

从材料3中的最新版《新型冠状病毒肺炎防控方案》可以看出，新版防控方案力图用最短的时间，最低的代价，将疫情控制在最小的范围，最大限度地统筹疫情防控和经济社会发展，尽可能保持公众正常工作和生活秩序的指导思想。

四、结束语

生活中处处皆可贝叶斯。社会热点问题会层出不穷，青年学生热衷于围观各类社会热点，但对社会热点的认识和解读常常缺少自己的见解和思考。普通大众受思想道德素质和科学文化素质的限制，又很容易人云亦云。在如今网络普及、信息爆炸的时代，教师的责任，已不仅是教会学生科学知识，还需要培养学员运用科学的思维、理性的方式来处置和对待社会热点问题，并勇于正确引导公众舆论。只有在大众思想道德素质和科学文化素质的不断提高中，整个社会文明才能逐步推进。