一种数值型的保留格式加密算法

王 浩 张永平 李同寒 樊林畅

(中国人民警察大学智慧警务学院 河北廊坊 065099)

随着信息科技快速发展,大量数据在互联网中流通,数据泄露事件层出不穷.数据库中的数据大多是以明文形式存储,如学习通的数据库泄露事件.传统的加密方法通常会扩展数据,需要通过修改数据库结构或应用程序存储加密后的数据.保留格式加密(format-preserving encryption, FPE)已形成一类新兴的加密方式,专门用于保护加密后数据与原始数据格式相同.

保留格式加密系统地提出是在2002年,Black等人[1]在密码学领域研究出3种基本的FPE构建方法:Prefix,Cycle-Walking和Generalized-Feistel,这3种方法奠定了保留格式加密算法的基本框架.之后,FPE 加密主要研究不同数据类型数据加密算法、改进已有加密算法存在的问题以及FPE的具体应用场景.

解决整数域的FPE算法主要有FFSEM[2]和基于 Type-2 Feistel网络的整数FPE[3],SM4-FPE[4];解决字符域的FPE算法主要有FFX[5]、BPS[6]、变长字符加密[7]等;解决任意正则语言的有CtE[8]和RtE[9];解决数据库中日期类型数据的有基于随机基准值的加密方案[10];解决中文域的FPE算法通过建立姓名域与整数域的双射,再利用改进的Cycle-Prefix方法进行加密的方案[11],还有使用CtE将中文编码为整数之后,再使用现有的整数FPE加密算法[12].这些FPE算法都是基于基础分组密码设计的.

现在的研究趋向于把复杂域的问题转换为简单域,即建立复杂型数据类型与数字型数据的双射关系,本质上这些算法都属于CtE.2016年,FFX被NIST收录,FFX在实际应用中比较广泛.之前提出的一些保留格式加密方案仍存在一些安全隐患,如使用相同的密钥和相同的明文总会产生相同的密文,所以近几年提出加入调整因子、基于泛化的方法使明文和密文呈现1对多的关系[13].在应用场景方面,FPE可以用于增强数据库的安全性[14]、数据脱敏[15]、金融信息安全、数据消毒、水印技术以及物联网通信[16]等.

可见,现有保留格式加密算法大多基于Feistel结构,使用基础分组密码构造伪随机函数,并且使用Cycle-Walking方法确保密文输出,执行1次保留格式加密算法需要执行多次基础分组密码算法,比基础分组密码效率低.每个FPE操作所需要的分组密码的迭代次数是不可预测的,存在不确定的性能问题.所以本文提出一种新的数值型FPE算法,通过构造多个不同的有限域使得每次运算都在数值型数据的消息空间内,从而避免使用Cycle-Walking,效率优于FFX算法.

1 算法描述

数值型消息空间为Σ={0,1,2,3,4,5,6,7,8,9},消息空间的大小为|Σ|=10,明文是消息空间内的元素组成的字符串,即明文只包含来自消息空间Σ中的元素.以下的消息空间指的就是大小为10的数字集合.

为了避免使用Cycle-Walking,在算法中构造有限域Fpb,其中p是素数,b是整数.由于消息空间大小为10,故选取F3上的不可约多项式P(x)=x2+1,构造F32=3[x]/(x2+1)={0,1,2,x,x+1,x+2,2x,2x+1,2x+2}域和F11域.F32一一对应F9={0,1,2,3,4,5,6,7,8}中这9个元素,F11={0,1,2,3,4,5,6,7,8,9,10},如无特殊说明,以下所说的F9都指F32=3[x]/(x2+1).

本文提出的数值型FPE算法在下文缩写为GFPE,表示基于不同代数群的保留格式加密算法.GFPE加密算法由10轮相同的混合变换和1个输出变换组成,是一种迭代型分组密码算法.该算法的明文长度为n,n≥2,初始密钥长度为128b.混合变换采用有限域和消息空间大小的群的代数运算,密钥扩展算法采用序列密码密钥生成器生成轮密钥,数据解密和数据加密的算法结构大致相同,只是轮密钥的使用顺序有所差异,部分运算使用其逆运算;最后通过一个输出变换获得密文.下面介绍加密算法、解密算法和密钥扩展算法.

1.1 加密算法

GFPE加密流程中主要用到3种运算和S盒非线性变换.

2) 模11乘运算⊙:a⊙b=(a×b) mod 11;

3) 模10加运算⊕:a⊕b=(a+b) mod 10.

F9域中的元素进行模加运算,明文中有可能出现不属于F9中的元素,为了保留格式提出置换算法(permutation algorithm, PA)和跳过算法(skipping algorithm, SA).F11域中的元素进行模乘运算,对任意1≤x≤10中的x模11乘法均有逆元,而0没有逆元,所以当输入为0时将其映射为10,输出为10时将其映射为0.

1.1.1 置换算法

消息空间大小为10,构造的有限域F9的大小为9,为了达到混淆和保证所有格式都存在的目的,在每轮轮函数的开始,根据置换密钥k0∈F9,使用元素9代替k0进行模加运算,即a∈10.对于k0≠9的情况,如果a和k0的值相同,则进行跳过算法,如果a=9,使用k0代替a进行模9加运算;对于k0=9的情况,如果a=9,则进行跳过算法.

例如移位密钥为k0=1,则F9中的元素1不参与本轮的模F9加运算中,如果输入为1,则执行跳位算法,如果输入为9,此时使用1代替9参与F9域模加运算.

通过在某一轮使用置换密钥代替不在F9有限域中的消息空间元素9,增加了混淆的不确定性,具有一定的非线性.

1.1.2 跳过算法

根据置换算法,在运算过程会出现置换密钥需要参与运算情况,如果使用置换密钥进行运算,则在解密时会出现1对多的现象,置换就没有意义,所以置换算法和跳过算法往往是同时出现的,两者相辅相成.

每轮的输入和中间输出都可能包含不在F9域中的元素,通过置换密钥,可知每轮不参与F9域运算的元素k0,当需要参与F9域运算且遇到k0时,则不作任何运算,中间结果就是其本身,即跳过运算,中间输出为k0,等到在其他代数群中进行状态转换运算.

例如k0=1,当F9域模加运算时的元素为1时,此时不加密,输出结果为1,1会在本轮之后的10群或者F11域中进行运算.

在每轮使用置换算法和跳过算法,对某些状态没有进行转换,所以会泄露轮函数的某些输入状态或者中间状态,即有可能泄露明文的某些信息,可能会降低每轮算法的复杂度,但是在不知道置换密钥的情况下会增加混淆的程度,则两者是成正比的.

1.1.3 S盒非线性变换

S盒通过置换产生混淆的非线性变换,主要目的是在密文中制造混乱.S盒的选择对分组密码的安全性至关重要,具有高差分均匀度和非线性度是S盒安全性的2个重要目标,体现了S盒的抗差分分析攻击和抗线性分析攻击的能力.构造S盒主要有2种方法:第1种是数学构造法,使用布尔函数或者有限域中的乘法逆函数;第2种方法是随机构造法,适用于较小的格式,可以穷举所有的S盒,分析线性和差分均匀性并选择高差分均匀度和非线性度的S盒.

本文使用随机构造法,在加密算法的设计中S盒不用可逆,故S盒是一个满射映射,即S:102→10,S盒的大小是10×10的.使用0～9之间的置换,建立一一映射关系,这样就会有10!中置换的方法,对S的所有可能的映射进行了差分和线性分析,构造的S盒如图1所示,S盒的最大差分概率为2-2.47.

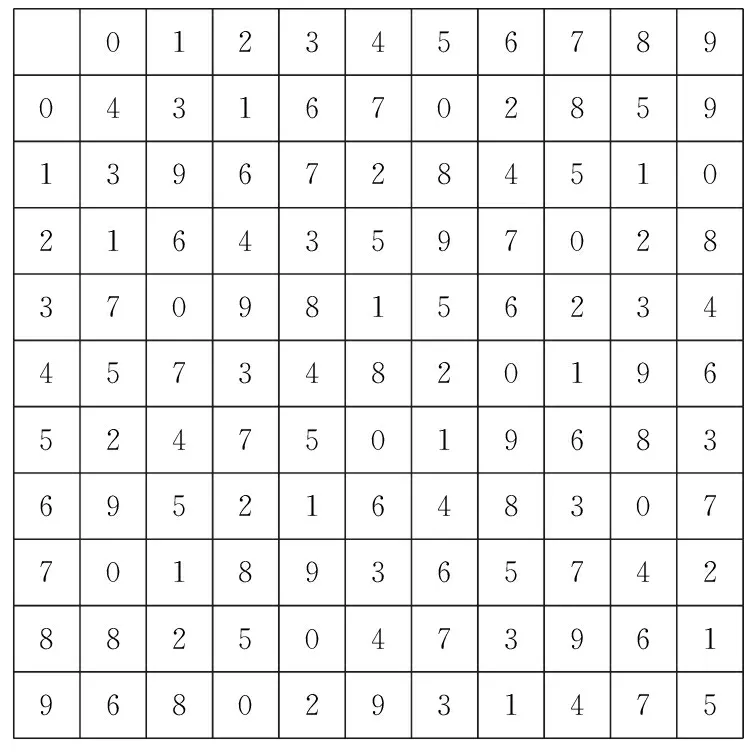
012345678904316702859139672845102164359702837098156234457348201965247501968369521648307701893657428825047396196802931475

1.1.4 加密流程

设明文为X=x1x2…xn∈明文长度为n,根据n的奇偶性使用不同的轮函数结构.

Step1.将明文数据划分为n段,即X=x1‖x2‖…‖xn,其中xi∈10.根据本轮置换密钥生成新的F9域元素

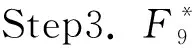
这3步得到Z1=z11‖z12‖…‖z1n.

Step4.判断n的奇偶性:若n为偶数,进行Step5;若n为奇数,分组个数加1,把z11连接在z1n之后,即Z1=Z1‖z11=z11‖…‖z1n‖z11,然后进行Step5.

Step5.|Z1|为偶数,相邻的奇偶位两两相减,即Z2i=z1i⊖z1(i+1),i=i+2,Z2=z21‖z23‖…‖z2(|Z1|-1).

Step7.|Z3|为偶数,两两放入S盒,奇数取S盒的行,偶数取S盒的列.即Si=S(z3i,z3(i+1)),i=i+2,则S=S1‖S3‖…‖S|Z3|-1.

Step8.判断n的奇偶性:若n为奇数,Z4i=Si-Si+2,i=i+2;若n为偶数,Z4i=Si.

Step9.Step3得到的结果加上Z4i,即yi=z1i⊕Z4i,yi+1=z1(i+1)⊕Z4i.

Step10.若n为奇数,最后一个yn=z1n⊕Z41.

得到第r轮的输出结果为Yr=y1‖y2‖…‖yn,这也是下一轮的输入.将(Yr)按照上述定义的轮变换进行迭代10轮,对第10轮的结果作最终的输出变换.

1.2 解密算法

本文提出的算法GFPE的解密过程和加密过程一样,不同的是轮密钥的顺序和置换密钥使用的位置.表1给出了解密密钥和加密密钥之间的关系.其中i代表第i轮运算,偶数位的K-1表示K的模(x2+1)的加法逆,即K+K-1≡0 mod (x2+1),奇数位的K-1表示K模11的乘法逆,即K×K-1≡1 mod 11.则加密密钥和解密密钥的对应关系如表1所示(以4轮为例):

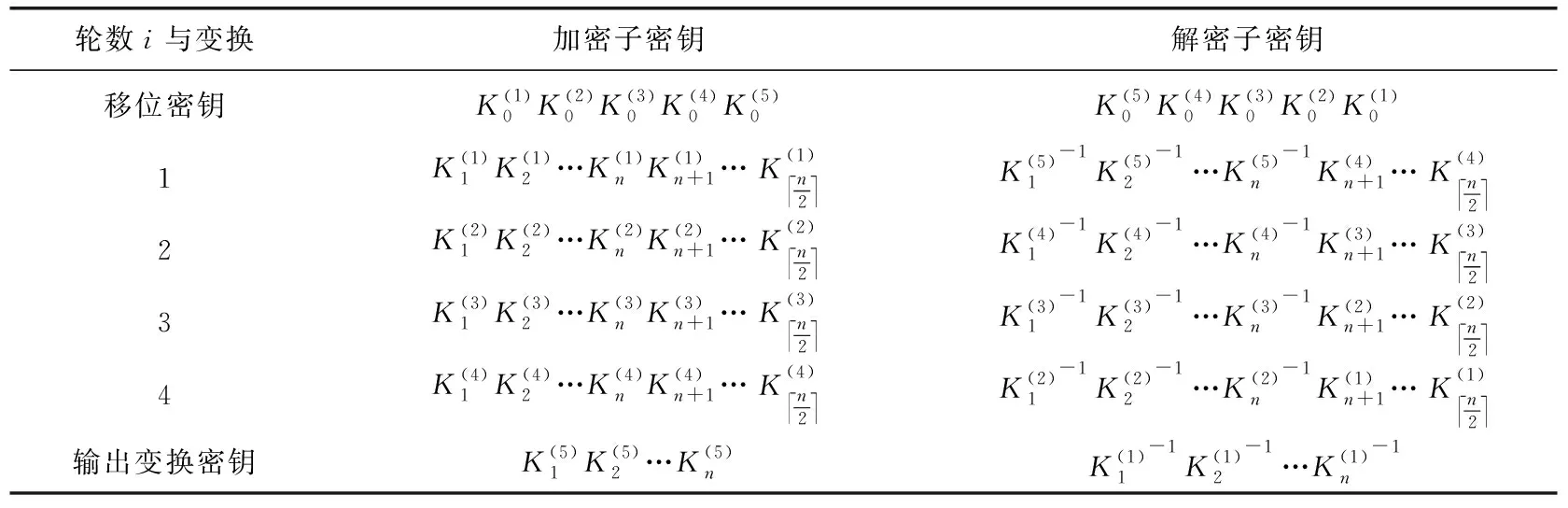
表1 加密轮密钥和解密轮密钥对应关系

由于置换密钥在1轮中,而输出变换中置换密钥也使用了置换密钥,所以进行解密时,置换密钥的顺序是相反的,在Step4之后,使用下一轮的置换密钥,最后的输出变换使用最后一轮的置换密钥.

1.3 密钥扩展算法

由于密钥格式不确定,针对GFPE密码本文提出一种新的保留格式密钥扩展算法.加密算法中使用的密钥由初始密钥生成,初始密钥K的长度为128b,如果明文的长度较长,可以对明文进行分段分别加密或者使用256b的初始密钥,本文以128b的长度为例.

加密过程需要用到2种密钥:移位密钥和轮密钥.移位密钥用于确定每轮的有限域中的元素,保证这一轮不在有限域中的元素会出现在下一轮中;轮密钥用于每轮轮函数的加密,轮密钥的长度需要根据明文分组的长度决定.每轮需要的加密密钥长度为明文的长度加上明文长度的一半向上取整.

2类密钥的生成算法基本一致,子密钥长度不确定,使用流密码密钥生成器产生子密钥.本文通过改进Salsa20算法的密钥生成函数,生成r轮子密钥.

1) 将128b初始密钥分为4组,每组32b,分别为k0=K127…K96,k1=K95…K64,k2=K63…K32,k3=K31…K0.

2) 首先运算

3) 移位密钥

K0=10r-1+(z0‖z1‖z2‖z3) mod (10r-10r-1).

4) 加密密钥生成方式如下:迭代上述步骤生成r+1个子密钥.

k0=z0,k1=z1,k2=z2,k3=z3,

(z0,z1,z2,z3)=Ri(k0,k1,k2,k3).

第i轮密钥为Ki=pb(n-1)+(z0‖z1‖z2‖z3) mod (pbn-pb(n-1)).

加密的轮密钥生成后,解密的轮密钥根据表1可以求出.

2 正确性验证

对于GFPE加密算法的具体实例,以偶数明文长度和奇数明文长度为例,为了说明过程,设定初始密钥为K=1234567890987654,每个十进制数转换为8b二进制数,一共128b的密钥,轮数r=4,实际应用中的轮数应根据明文长度来确定.

2.1 明文长度为偶数

输入:明文X=15748263,8位十进制数.

输出:8位十进制数.

2.1.1 加密

把明文X=15748263划分为8个10以内的数字:x1=1,x2=5,x3=7,x4=4,x5=8,x6=2,x7=6,x8=3.

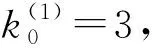
当r=2,3,4时,前一轮的输出作为下一轮的输入,同理得到输出结果为:

Y=(2,6,3,5,6,9,2,6).

最终得到密文Y=26356926.

2.1.2 解密

把密文Y=26356926划分为8个10以内的数字:x1=2,x2=6,x3=3,x4=5,x5=6,x6=9,x7=2,x8=6.

当r=2,3,4时,前一轮的输出作为下一轮的输入,同理得到输出结果为:

X=(1,5,7,4,8,2,6,3).

最终得到明文X=15748263.

2.2 明文长度为奇数

输入:明文X=15748,5位十进制数.

输出:5位十进制数.

2.2.1 加密

把明文X=15748划分为5个10以内的数字:x1=1,x2=5,x3=7,x4=4,x5=8.

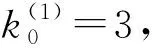
当r=2,3,4时,前一轮的输出作为下一轮的输入,同理得到输出结果为:

Y=(4,8,8,3,0).

最终得到密文Y=48830.

2.2.2 解密

把密文Y=48830划分为5个10以内的数字:x1=4,x2=8,x3=8,x4=3,x5=0.

当r=2,3,4时,前一轮的输出作为下一轮的输入,同理得到输出结果为:

X=(1,5,7,4,8).

最终得到明文X=15748.

3 安全性分析

对于保留格式加密安全性的描述最早是由Black等人[1]提出的PRP(pseudo random permutation)安全,即伪随机置换安全.要求攻击者把保留格式加密方案和消息空间内的随机置换区分开.本文通过差分密码分析和相关密钥攻击,得出r=10对所有的实例是安全的结论.

3.1 差分密码分析

差分密码攻击是迭代型分组密码最有效的攻击方式之一.差分分析主要关注的是非线性函数,本文提出的GFPE算法的非线性过程包括S盒、F9域模加和F11域模乘.

在差分密码分析中,通过选择具有特定输入差分α的明文对(X,X*)使得最后一轮的差分ΔY(r-1)以高概率输出为特定的值β.给出以下的定义:

定义1.差分对.(α,β)为分组密码的1个i轮差分对,其中α是1对不同的明文X和X*的差分值,经过i轮加密,输出对Y(i)和Y(i)*的可能差分值为β.

定义2.差分概率.当明文X和轮密钥K1,K2,…,Ki取值独立且均匀分布的情形下,给定明文对(X,X*)的差分值为ΔX=α,则第i轮输出对(Y(i),Y(i)*)的差分值为ΔY(i)=β的概率为迭代分组密码的1条i轮差分(α,β)的概率,记为DP(α,β).特别地,当i=1时,DP(α,β)表示轮函数的差分传播概率.

定义3.差分特征的级联.给定2条差分特征Ω1=(β0,β1,…,βs),Ω2=(γ0,γ1,…,γt),若βs=γ0,则称Ω=(β0,β1,…,βs,γ1,γ2,…,γt)为Ω1和Ω2的级联,记为Ω=Ω1‖Ω2,此时,DP(Ω)=DP(Ω1)×DP(Ω2).

由文献[17]可知,具有弱轮函数的m位十进制数的r轮迭代密码抵抗差分攻击的充分必要条件是r-1轮差分中没有一个概率显著大于10-m.所以需要找到r-1轮中的最大差分传播概率小于10-m,这样进行差分密码攻击所需的数据就会超过可用数据.

使用GFPE(m)代表GFPE算法加密m位十进制数,以GFPE(2)为例进行差分分析,F9域和F11域的差分最后会和S盒进行一个复合运算,S盒和这两者相互独立.分析经过F9域和F11域的运算后再复合到S盒输出差分的基本性质:

S=SBox(row,column);

S*=SBox(row*,column*).

根据上述描述,对GFPE(2)进行穷举实验,计算出90×90的差分传播概率矩阵,得到1轮GFPE(2)算法的最大差分概率为0.041759.根据差分特征的级联定义,可以得出对于GFPE(2)加密算法,任意4轮进行差分密码攻击所需的数据超过可用数据.

同理,对GFPE(4)进行差分分析,输入差分和输出差分的性质与GFPE(2)类似,仅仅增加了位数和密钥.对于GFPE(4),其差分传播概率矩阵大小为9000×9000,穷举实验时间较长,故在文献[17]提出的“随机等价假设”原则之下,讨论GFPE(4)算法的差分传播概率,即假设对大多数密钥而言,固定密钥下的差分传播概率与各轮密钥相互独立且随机均匀分布时的差分传播概率近似相等,表示为DP[k1,k2,…,kr-1](α,β)≈DP(α,β).

在“随机等价假设”原则之下,计算出一轮GFPE(4)算法的最大差分概率为0.14122,则对任意6轮进行差分密码攻击的数据需求将超过可用数据.

3.2 相关密钥攻击

相关密钥攻击是最重要的密钥相关攻击之一.为了发起相关的密钥攻击,攻击者利用不同子密钥之间有意义的关系,从而可以在一定轮次上构造相关的密钥差异.

GFPE算法的密钥扩展算法中使用非线性加运算和异或运算,为了能够弹性输出固定位数的轮密钥,在密钥调度算法的每轮使用了模运算,攻击者不能从1轮子密钥中推导出其他所有轮的密钥,更不可能推导出主密钥.特别是模运算使得攻击者不能确定不同轮的差异传播规律,主密钥依然是安全的.此外,对于消息空间大小为10的数值型数据,密钥扩展算法在第5轮中使用初始密钥K的每一位.基于密钥扩展算法可以得出结论,该密钥扩展算法能够抵抗相关的密钥攻击.

而且GFPE算法的密钥长度是128b,对于穷举密钥搜索攻击来说,需要进行2128次加密运算,则使用10亿个每秒能测试10亿个密钥的芯片并行处理需要花费1013年破解出密钥.即1024个这样的芯片在1天内能找出密钥,显然目前没有这样的实力造这样的一个机器,故GFPE算法可以达到实际安全性的要求.

4 效率分析

应用最广泛的保留格式加密算法是NIST保留格式加密标准FFX[18],基于Feistel结构,轮数为8,需要调用8次基础分组密码,会降低基础密码算法的效率,本文实验选用基础分组密码AES,分组长度是128b,128b可以转换为32位十进制数字.

本文提出的保留格式加密算法不需要结合Cycle-Walking,只需要进行多次轮函数运算,效率显著降低.实验环境为:Matlab R2018a,CPU为Intel®CoreTMi7-10750H,主频为2.60GHz,内存为32.0GB.

GFPE的密钥为128b,加密32位十进制数字时每轮会使用到密钥的所有位数,所以分别计算1000条2～32位不同明文长度下算法的加密时间,计算其平均时间,实验的效率对比如图2所示:

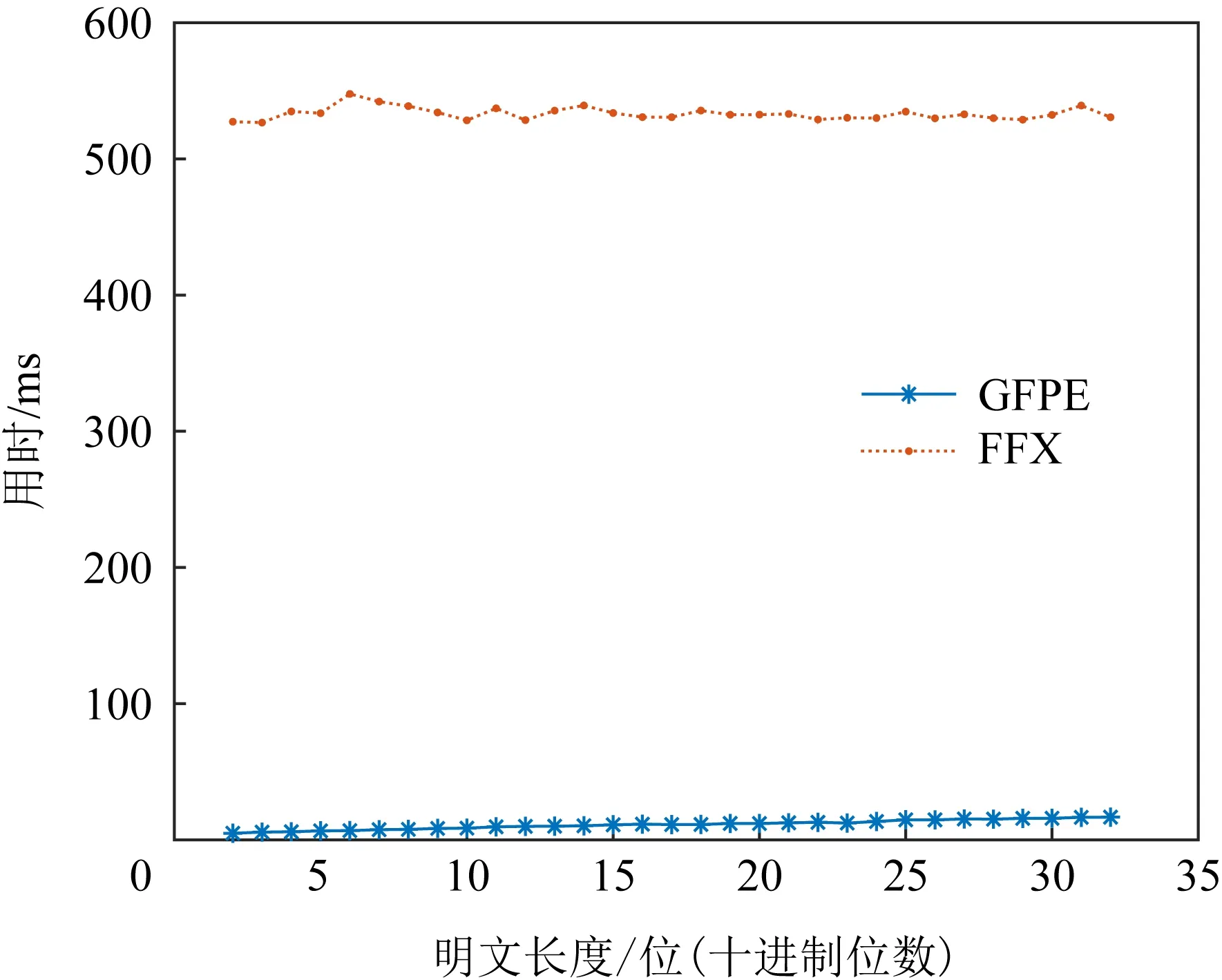
图2 效率对比

实验结果表明:随着明文长度的增加,本文提出的算法用时缓慢增加,FFX用时基本稳定;在相同明文长度下,算法效率远远大于FFX的效率.在一个分组128b数字(32位十进制数)下,本文算法效率大约是FFX的30倍,显著提高了保留格式加密算法的效率,应用前景广泛.

为了增强数据库系统的安全,大多数应用依赖数据库系统.金融支付[19]、电子商务[20]、社保、教育系统以及网上支付等数据库应用系统中存在大量敏感信息,如银行卡号、电话号码、身份证号等,保留格式加密算法不破坏数据库结构和不改动软件代码,加强数据库安全的同时节省大量资源.此外,还可用于数据遮蔽和支付卡行业,将真实数据伪装为加密之后的数据,使假数据看起来是真数据,保护个人信息.

5 结 语

本文提出了一种数值型数据保留格式加密算法,能对超过1位的任意位数值型明文进行保留格式加密,保证数值型明文加密为长度相同的数值型密文,且在有限的计算能力范围内达到实际安全性的要求.和传统的保留格式加密算法相比,该算法不使用Cycle-Walking,极大地提高了FPE算法的效率,具有广阔的应用前景,能增强数据库中数值型敏感数据的安全,也可在数据遮蔽和金融支付中避免数据泄露,保护隐私.

下一步要做的工作是优化算法的结构,使随着明文数据长度的增加,算法使用的时间是趋于稳定的,并且探究如何对所有数据类型都适用的保留格式加密算法.