微型动力调谐陀螺挠性接头的优化设计

吴 晨 郭宝林 张培新 李 伟 武 展

微型动力调谐陀螺挠性接头的优化设计

吴 晨 郭宝林 张培新 李 伟 武 展

（西安航天精密机电研究所，西安 710000）

挠性接头是动力调谐陀螺中的核心部件，其性能直接决定陀螺性能。作为微型动力调谐陀螺用挠性接头，既要体积小，又要具备一定角刚度。为了提升挠性接头性能，减小某型号微型动力调谐陀螺随机振动漂移量，本文首先建立了挠性接头优化问题的数学模型，然后介绍了BP-GA优化算法，并将其应用在挠性接头优化设计中，同时实测了优化后挠性接头性能，最终经过陀螺随机振动试验验证表明，优化后挠性接头对应陀螺的随机振动漂移量从1.5°/h下降到0.09°/h，效果显著。

微型动力调谐陀螺;挠性接头;BP-GA算法;优化设计;角刚度;随机振动漂移

1 引言

动力调谐陀螺是一种通过动力效应补偿陀螺转子正刚度的二自由度陀螺仪。挠性接头是动力调谐陀螺的核心零件，陀螺正常工作时，挠性接头的性能直接影响动力调谐陀螺的精度、可靠性、寿命等关键参数[1，2]。近年来随着武器装备的快速发展，许多领域对动力调谐陀螺用挠性接头提出了更高的要求，不仅需要其具备性能优良的特点，还需要其具有超小体积，从而减小陀螺本体的体积大小。国外在微型动力调谐陀螺用挠性接头的设计上早已趋于成熟，并将其应用于航天、航海、航空体系，如星际飞行器和地球资源卫星等。国内在微型动力调谐陀螺用挠性接头的设计及制造与国外仍存在差距，如挠性接头在超小体积下，仍保持高性能、高稳定性等。冯永星等研究了挠性接头细颈倾角对其力学性能的影响[3]，星玉华等对挠性接头零件断裂进行了失效分析[4]，贺新华等对挠性接头在陀螺中的质量控制进行了研究[5]。但均没有涉及对挠性接头结构上的优化设计，尤其针对微型动力调谐陀螺用挠性接头，既要求体积小，又要求具备较大的角刚度，从而保证陀螺具有较好的抗环境适应能力。本文首先建立了挠性接头优化问题的数学模型，然后介绍了BP-GA优化算法，并对挠性接头进行了优化设计，最终通过挠性接头性能实测以及陀螺随机振动试验，对优化后挠性接头性能的提升进行了验证。

2 优化模型建立

微型动力调谐陀螺中使用的挠性接头主要由内挠头、外挠头组合而成，如图1所示，特点是内、外挠头上对应细颈相互正交，从而形成陀螺转子组件支承平面。

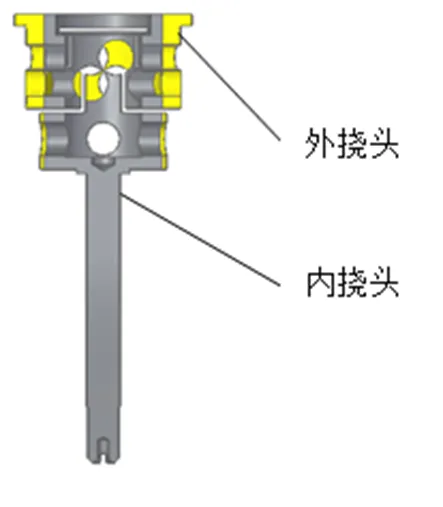
图1 挠性接头组件

对于挠性接头而言，其角刚度是一个重要参数，为了达到陀螺的动力调谐，挠性接头的角刚度必须满足：

=(-/2)2（1）

式中：为挠性接头角刚度；为陀螺转子赤道转动惯量；为陀螺转子极转动惯量；为陀螺转子转速。

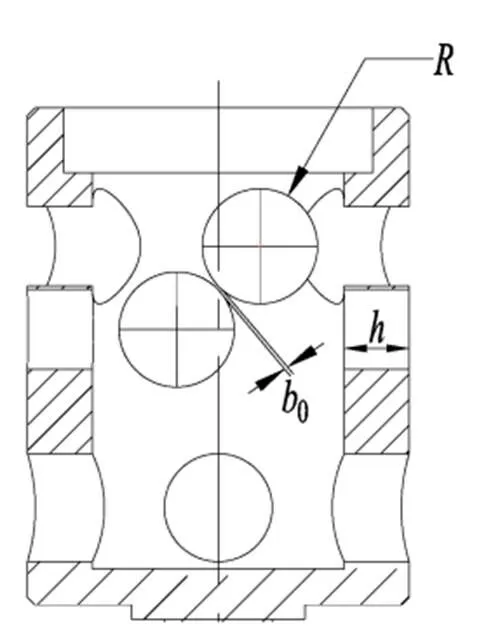
图2 挠性接头参数化示意图

同时为了提升微型动力调谐陀螺的抗环境适应性，减小陀螺的随机振动漂移量，对应挠性接头需要具备较大角刚度，而挠性接头的角刚度是由其细颈切割半径、细颈宽度0、厚度、材料弹性模量E决定的，如图2所示。

挠性接头角刚度可以表示为：

=(,,0,) （2）

某微型动力调谐陀螺外形尺寸仅为21.4mm×30mm，为了解决陀螺目前存在随机振动漂移量较大的问题，其配套挠性接头既要体积小，又要具备较大刚度，然而两者往往相互制约，因此，需要从挠性接头结构尺寸上着手，对其进行优化设计，使其满足微型动力调谐陀螺的设计要求。带有约束条件的结构优化设计问题可描述为：

Min() （3）

g()≤0=1,2,…,（4）

h()=0=+1,…,（5）

a≤x≤bi=1,2,…,（6）

其中：=[1,2,…,x]∈R是维实向量，()为目标函数，a≤x≤b为区域约束条件，g()、h()为约束函数，其中不等式约束条件数量为个，等式约束条件数量为～个。

针对挠性接头，需要设计一组最优的几何参数、0、，使其角刚度大于120g·cm/rad，并且体积最小，即：

Min(,0,) （7）

(,0,)＞（8）

针对上述目标，构造了目标函数()：

()=()+|()-| （9）

此处设计变量=[,0,]，约束条件为∈[0.5,1.5]；0∈[0.03,0.05]；∈[0.5,1.5]，式中单位均为mm。

3 BP-GA算法

3.1 人工神经网络及BP算法

人工神经网络是模拟人大脑中数以百万计神经元的复杂网络，T. Kohonen将其定义为：相互连接并且具有适应性的网络，其可以模拟真实神经元对外界的反应[6]。

人工神经元是人工神经网络的基本单元，如图3所示，具有多输入单输出的特性。

图3 基本神经元模型

=[1,2,…P]T是输入向量，表示其它神经元的轴突输出，=[1,2,…]是权值向量，代表该神经元R个突触与其它神经元的连接强度，为阈值，为神经元的传递函数，从而神经元的基本模型可表示为：

=(∑i=1ωp-) （10）

BP算法具有多层网络的特点，无需建立数学模型，只通过样本数据就可以建立起输入与输出之间的非线性映射关系[7]。采用BP算法的网络学习分为两个阶段，正向传播和反向传播，以上两个过程反复进行，直到达到收敛为止。

3.2 GA算法

GA算法是一种高效、并行、全局的搜索方法，其基本过程是通过选择、保留、遗传的方法，不断迭代群体质量，使群体中质量最高的个体对应问题的最优解[8]，如图4所示，显示了GA算法优化的基本过程。

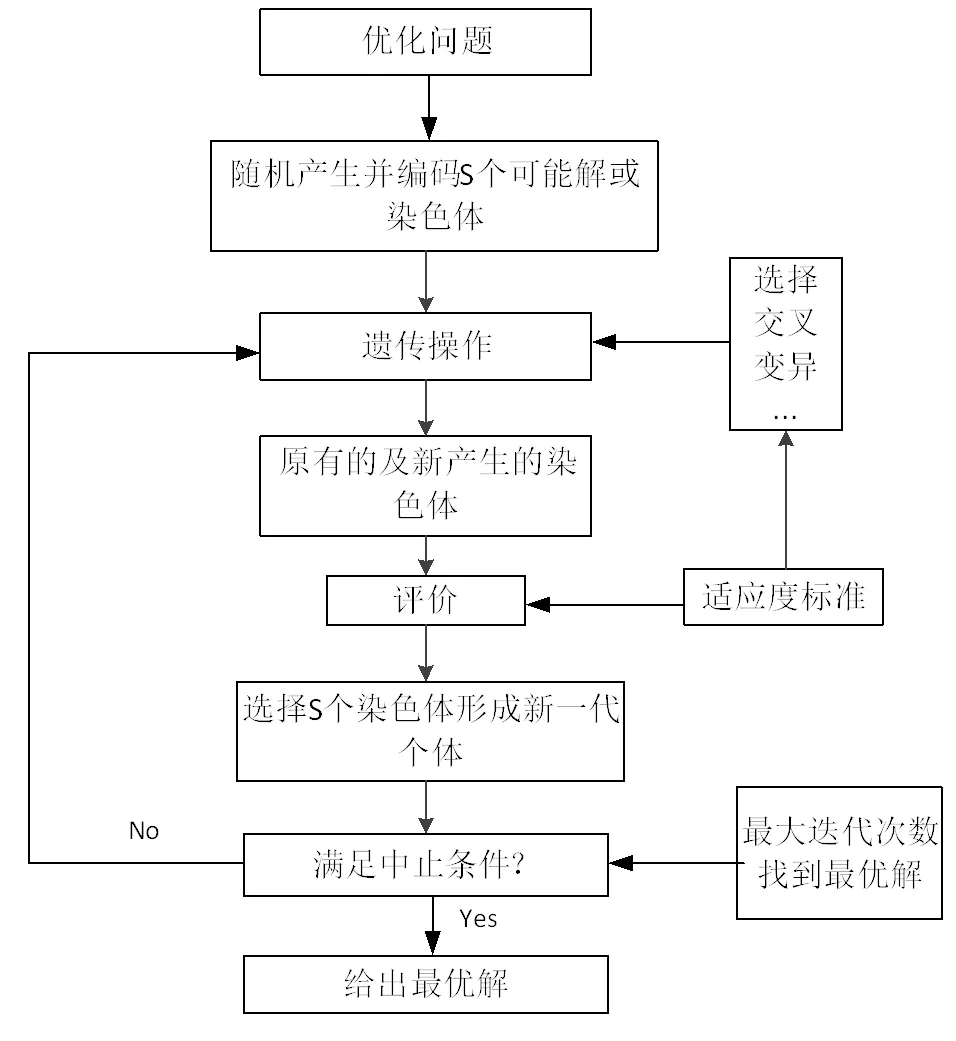
图4 遗传算法示意图

GA算法在结构优化设计过程中需要大量的有限元计算，因此如何提高计算效率是GA算法在应用中的关键问题。

2.3 基于BP-GA算法的优化方法

BP-GA算法是将神经网络BP算法与GA算法的优势结合起来，运用BP算法建立设计变量和目标函数之间映射关系，进而提升GA算法的计算效率[9，10]，其计算流程如图5所示。

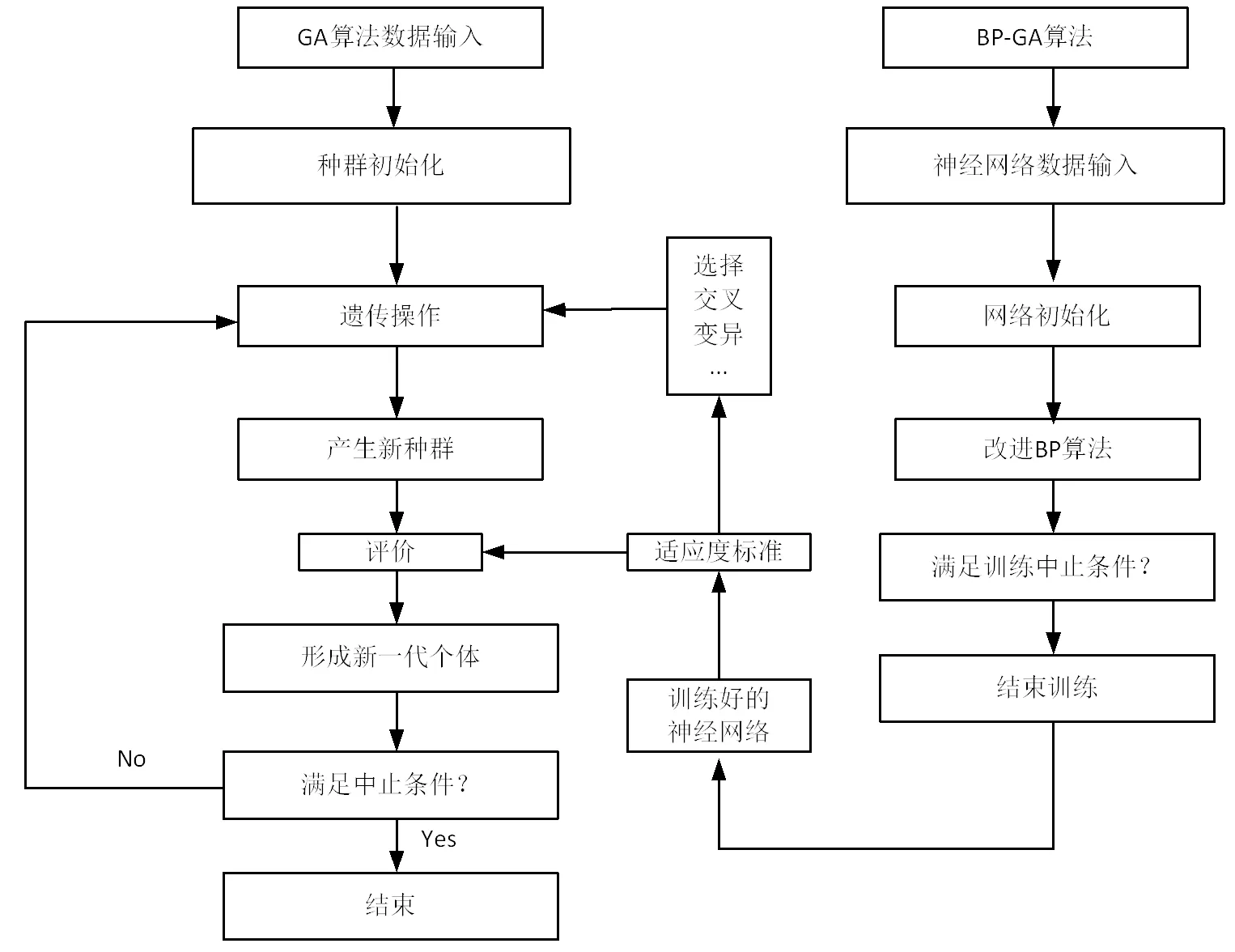
图5 BP-GA算法流程

近年来， BP-GA算法已被成功应用在结构优化设计问题上，如郭海丁等运用BP-GA算法对发动机关键零部件结构进行了优化设计[11]，林琳等运用BP-GA算法对复杂结构进行了轻量化研究[12]，吴小光等运用BP-GA算法对滑行艇船外形进行了优化设计[13]。BP-GA算法已成为工程问题中结构优化设计的关键算法。

4 BP-GA算法求解挠性接头优化设计问题

4.1 训练样本的建立

根据设计参数，0，的约束区域，取均布的三个水平，进行解析计算，求出挠性接头细颈的角刚度和体积，如表1所示。

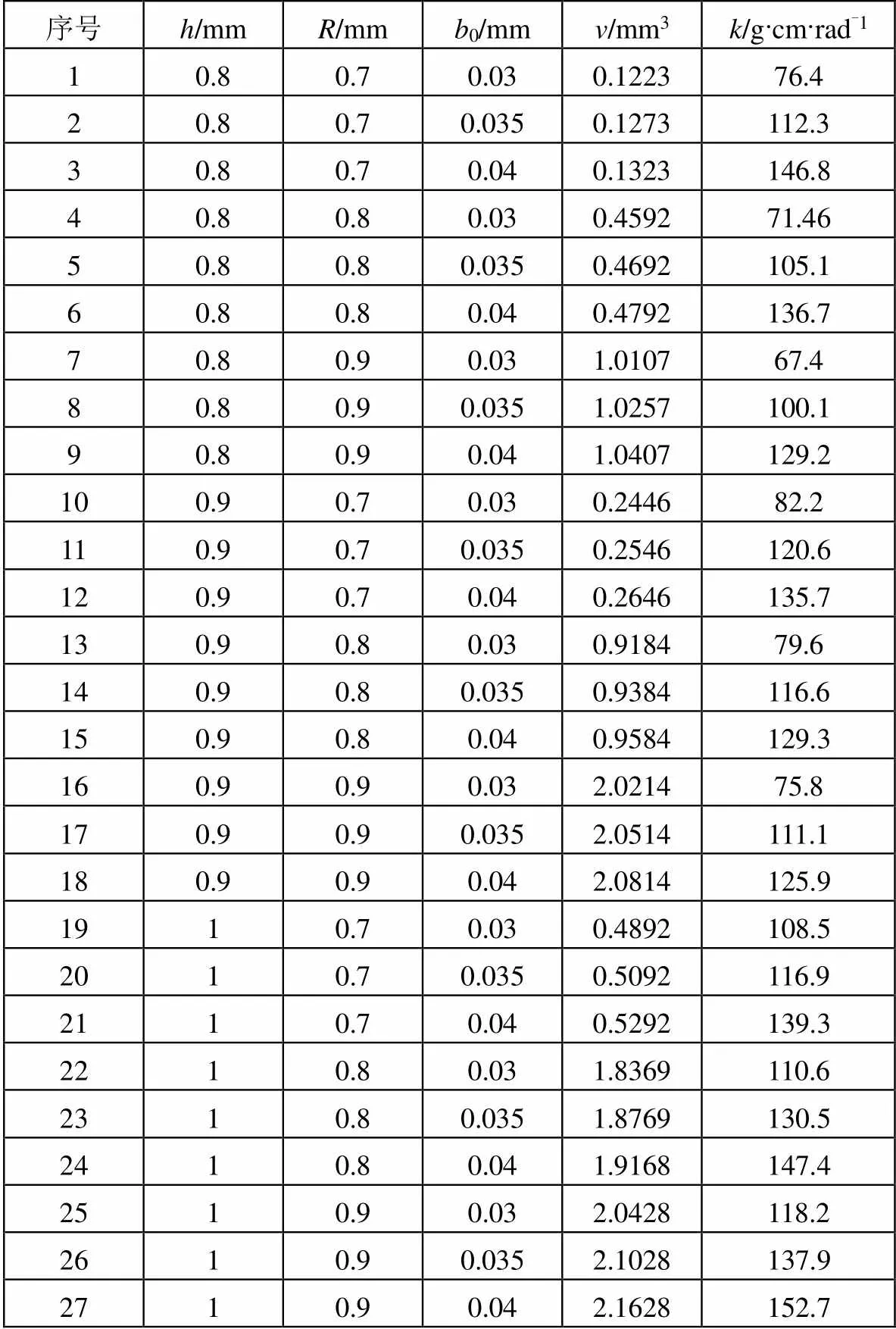
表1 BP-GA算法的训练样本数据

表1中的数据，用于对BP神经网络进行训练。

4.2 BP神经网络的训练

在运用BP神经网络算法时，首先需对其进行训练。训练中止条件为：均方差≤10-5，或者训练次数达到104，其中学习因子为0.01。图6所示为神经网络的训练效果。

图6 样本目标和神经网络输出

图6中“*”为BP算法中样本目标值，实线为输出值。显然，两者基本吻合，可认为BP算法逼近了目标非线性函数

4.3 优化结果

基于BP-GA算法对挠性接头进行优化设计过程中，初始群体大小为20，交叉率取0.6，变异率取0.09，经过100次迭代后，最佳适应值趋于稳定，此时对应的优化解为：=0.8517mm、=0.9012mm、0=0.0372mm，将优化结果圆整为工程值：=0.85mm、=0.9mm、0=0.037mm，优化后挠性接头与现有挠性接头结构参数对比如表2所示。

表2 优化后参数与原参数对比

显然，优化后挠性接头角刚度在原有基础上增加了13.2%，达到了132.1g·cm·rad-1，且挠性接头体积并未增加，反而在原结构基础上减小了19.3%，仅为1.722mm3，满足挠性接头优化设计目标。

4.4 优化后挠性接头实测

为了进一步验证优化后挠性接头的角刚度是否满足计算要求，分别加工了优化前后挠性接头实物各3件，如图7所示。

图7 优化前后挠性接头对比

图8 挠性接头角刚度测试系统

利用振动测试技术，对其角刚度值进行了实测。挠性接头角刚度的测试系统由3个部分组成，分别为激振、拾振以及分析显示部分。激振装置可对被测对象施加往复的振动，由于挠性接头体积小，因此激励方式采用单点激励，通过机械单点波动使挠性接头发生往复运动的弹性变形。在挠性接头刚度测试过程中拾振装置是其中的关键环节，其能够对振动输出进行数据采集，在并对其相应信号进行处理[14，15]，本文采用高精度激光位移传感器对振动信号进行测量，具体测量过程如图8所示

经过测试后，原挠性接头角刚度为115.2g·cm/rad，优化后挠性接头角刚度为130.3g·cm/rad，与计算值基本吻合，因此，优化后挠性接头符合设计要求，且具备工程生产条件。

5 试验验证

为了验证优化后挠性接头在微型动力调谐陀螺上的性能，将优化前后各3件挠性接头装配成6块陀螺，如图9所示，表3为各陀螺对应表号。

图9 优化前后挠性接头对应陀螺

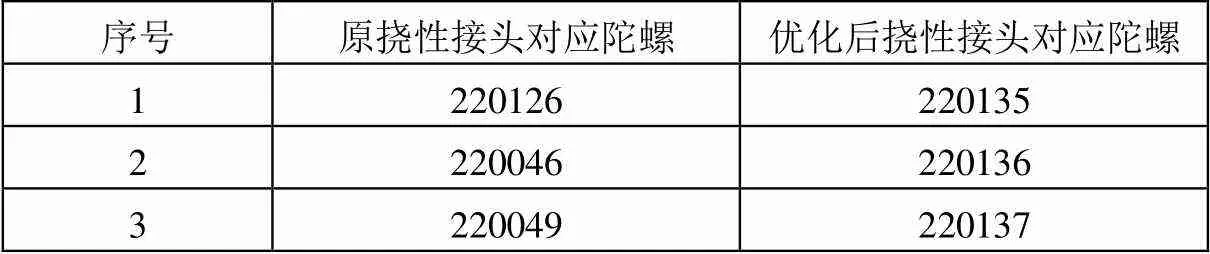
表3 优化前后挠性接头装配陀螺对应表号

陀螺装配完成后，分别对其进行随机振动试验，试验曲线如图10所示，其中，振动方向均沿陀螺轴，振动时间为5min。

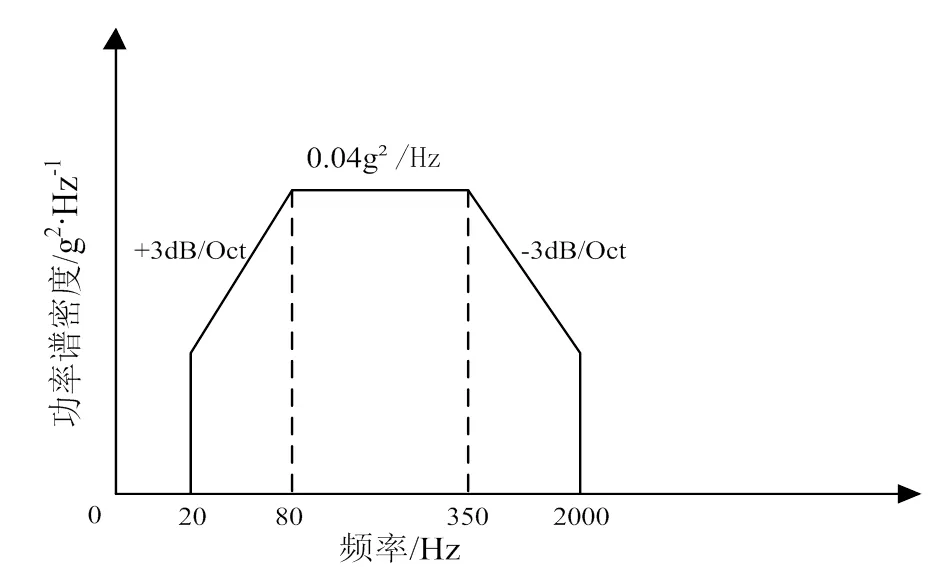
图10 随机振动试验条件

振动过程如图11所示。

图11 陀螺随机振动过程

陀螺随机振动漂移量的定义为：陀螺振动过程中输出的最大变化量对应角速率，可通过式（11）进行计算。

=Δ/（11）

为陀螺随机振动漂移量，°/h、为陀螺标度因数，单位为mV/(°/h)、Δ为随机振动试验中陀螺输出的最大变化量，。

某微型动力调谐陀螺标度因数为100mV/(°/h)，经过随机振动试验后，6块陀螺输出最大变化量及随机振动漂移量如表4所示。

表4 优化前后对应陀螺随机振动漂移

显然，优化后挠性接头对应陀螺的输出最大变化量从150mV下降到9mV，其随机振动漂移量从最大1.5°/h下降到最小0.09°/h，效果显著。

6 结束语

本文针对微型动力调谐陀螺挠性接头多参数优化设计问题，通过建立挠性接头优化问题数学模型，引入BP-GA算法，对其结构参数进行了优化设计，并对优化结果进行了测试验证，最后将优化后挠性接头装上动力调谐陀螺，经过随机振动试验验证，陀螺随机振动漂移量从最大1.5°/h下降到最小0.09°/h，有效提升了微型动力调谐陀螺的性能指标。

1 林士鄂. 动力调谐陀螺仪[M]. 北京：北京国防工业出版社，1983

2 周百令. 动力调谐陀螺仪设计与制造[M]. 南京：东南大学出版社，2002

3 冯永星，刘涛，牛红燕，等. 细颈倾角对挠性接头力学性能影响分析[J].应用力学学报，2012，29(4)：445～450

4 星玉华，李靖，付明. 挠性接头零件断裂失效分析[J]. 材料保护，2018，51(4)：141～142

5 贺新华，田梦君. 挠性陀螺仪内外接头的质量控制[J]. 机械与电子，2010，10(2)：4～9

6 Kohonen T. Self-organization and associative memory[J]. Machine Design，2014，29(2)：76～79

7 周开利，康耀红. 神经网络模型及其MATLAB仿真程序设计[M]. 北京：清华大学出版社，2005

8 Goldberg D E.Genetic Algorithms in Search Optimization and Machine Learning[J]. Mechanism and Machine Theory Design，2009，37(1)： 477～498

9 陆金桂. 基于人工神经网络结构近似分析方法的研究[J]. 中国科学A辑，2014，24(6)：653～658

10 张延年. 工程结构优化设计的改进混合遗传算法[J]，吉林大学学报，2022，35(1) ：65～69

11 郭海丁，路志峰. 基于BP神经网和遗传算法的结构优化设计[J]. 航空动力学报，2013，18(2)：10～18

12 林琳，张云波. 基于MATLAB的桁架结构优化设计[J]. 低温建筑技术，2003，8(1)：34～36

13 吴晓光. 滑行艇船优化设计[J]. 船舶工程，2005，27(3)：15～19

14 吴冬良，戴一帆，郑子文. 基于模态分析的挠性接头角刚度测量研究[J].国防科技大学学报，2004，26(5)：94～98

15 杨元华. 挠性接头刚度动态测试方法研究[D]. 哈尔滨：哈尔滨工业大学，2002

Optimization Design of Flexible Joint of Miniature Dynamically-tuned Gyroscope

Wu Chen Guo Baolin Zhang Peixin Li Wei Wu Zhan

(Xi’an Aerospace Precision Mechatronics Institute, Xi’an 710000)

The flexible joint is the core component of the dynamically-tuned gyroscope, and its performance dircetly determines the performance of the gyroscope. As a flexible joint for a miniature dynamically-tuned gyroscope, it must be small in size and have a certain angular stiffness. In order to improve the performance of flexible joint and ruduce the random vibration drift of a miniature dynamically-tuned gyroscope. This paper establishes a mathematical model for the optimization problem of flexible joint firstly, and then introduces the BP-GA optimization algorithm, which is applied in the optimization design of flexible joint and then the performance of the optimised flexible joint has been measured. The final random vibration test of the gyro shows that the random vibration drift of gyro which the flexible joint has been optimizatized decreases from 1.5°/h to 0.09°/h, the effect is remarkable.

miniature dynamically-tuned gyroscope；flexible joint；BP-GA algorithm；optimization design；angle stiffness；random vibration drift

O318

A

装备预先研究项目（51309010603）。

吴晨（1990），硕士，航空宇航制造工程专业；研究方向：陀螺仪总体设计。

2023-05-19