基于模拟退火算法的储油罐变位识别模型

张万菊 姚凯学 何 勇 席雷鹏

(贵州大学计算机科学与技术学院 贵州 贵阳 550025)

0 引 言

目前我国储油罐数量众多且存放地理位置较为分散[1],尤其是近几年来,为了满足社会经济发展的需要,我国公路、桥梁、高速路等施工建设行业得到大力发展,这些修建工地地理位置通常都比较分散且偏僻。工地上使用的挖掘机、铲车、大卡车等大型工程车需消耗大量柴油,若将工程车直接开到加油站,不仅要浪费油料和时间,而且也有诸多不便,因此,通常在工地现场安装储油罐,使工程车可以方便加油,提高工作效率和经济效益。偏僻的地理位置使得工地上的储油罐常存在被偷油、漏油无人察觉、人工记录数据混乱、油料补添不及时的情况,因此,需要对储油罐油位高度变化与出油量情况及油罐中剩余油量进行实时无人在线远程监测。

影响储油罐监测精确度的一个重要因素是储油罐在使用一段时间后,很多会由于地基变形导致变位(即油罐横向倾斜α角或纵向倾斜β角),从而出现储油罐罐容表不准确的情况[2-3],同时导致油位变化与出油量不匹配。针对罐容表不准确的情况,许多学者采用定积分的方式建立倾斜储油罐油位高度和储油量之间的数学模型,并采用误差补偿方法[4]、非线性最小二乘法[5]、蒙特卡洛算法[6]、Lagrange插值法[7]、神经网络[8]、遗传BP网络[9]等方法求解所建立模型中的最优变位角度,修正模型后对罐容表做标定,取得了相应的研究成果。

本文采用定积分的方式,建立了发生变位后的储油罐油位高度变化量、变位角和出油量之间的数学模型,采用非线性最小二乘法建立求解该模型最优变位角的目标函数,并利用模拟退火算法和MATLAB寻找模型中的最优倾斜角。从2010年全国大学生数学建模竞赛A题中随机选择400组数据求解出最优变位角,用剩下的100数据对矫正后的数学模型做检验,证明了该模型参数辨识方法的正确性。通过与实测数据、文献[9]和文献[10]中所使用方法的实验结果对比,证明了本文建立的数学模型可以更好地反映油位变化和出油量的关系,对于工地上防止偷油、漏油及监测油量变化是否正常的情况有很好的作用。

1 定积分建立变位数学模型

目前工地上使用最为广泛的储油罐是圆柱形和椭圆柱形卧式储油罐。本文通过对使用较为广泛的卧式圆柱形储油罐的分析,根据发生纵向和横向倾斜变位的油罐几何形状及油面,采用定积分的方式建立储油罐油位高度变化、变位角和出油量之间的数学模型。

1.1 纵向倾斜

储油罐柱体半径为R,油位探测针到左侧球冠体距离为l1,到右侧球冠体距离为l2。根据储油罐发生纵向倾斜α角后的几何形状及不同油位高度下油面的形状,对储油罐做分段处理。油罐分段和坐标示意图如图1所示。

图1 纵向倾斜油罐分段示意图

油位高度从h1(油位高度为从罐底向Z轴正方向的高度)下降到h0的体积变化即为储油罐的出油量Δv。

Δv=Δv左冠+Δv柱体+Δv右冠

(1)

油位高度为h,油平面z(y)满足关系:

z(y,h)=-ytanα+h-R

(2)

油位高度变化处于区域v1和v5内时,油位高度超出油位探测针的测量范围,出油量与油位高度变化关系无效,且油面几乎不会处于这两个区域内(正常使用下),因此忽略这两个区域的油位变化和出油量的关系。

(1) 柱体部分出油量计算。储油罐柱体部分v2、v3、v4区域内油位高度从h1下降到h0的出油量分别为:

当0≤h≤l2tanα时,即油位在v2内。

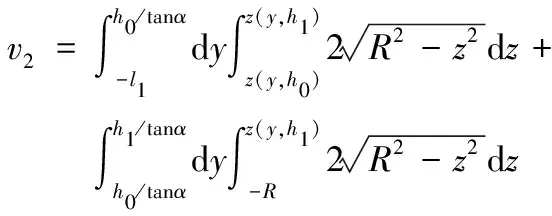
(3)

当l2tanα≤h≤2R-l1tanα时,即油位在v3内。

当2R-l1tanα≤h≤2R时,即油位在v4内。

(2) 球冠体部分出油量计算。储油罐两端的球冠体高为H,半径为r,当油罐倾斜α角时,左侧部分球冠体油位变化对应油面及坐标示意图如图2所示。

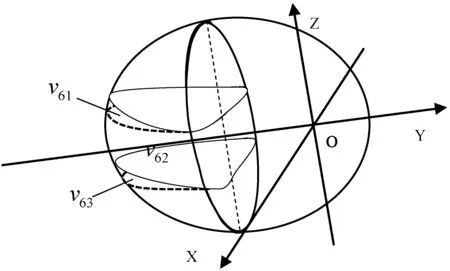
图2 左球冠体油位对应油面

由图2可知,左侧球冠体油位高度从h1下降到h0的理论出油量Δv左为:

Δv左=v61+v62-v63≈v62

(6)

其中:

同理,当油位高度从h1下降到h0时,右侧球冠体的理论出油量为:

式(7)、式(8)中的y为:

1.2 横向倾斜

根据卧式圆柱形储油罐的几何形状可知,油罐发生横向倾斜时,液面形状及油位高度均无变化[11],倾斜前后的油位测量值代表的出油量不同。横向倾斜后油罐内油位探测针的位置如图3所示。

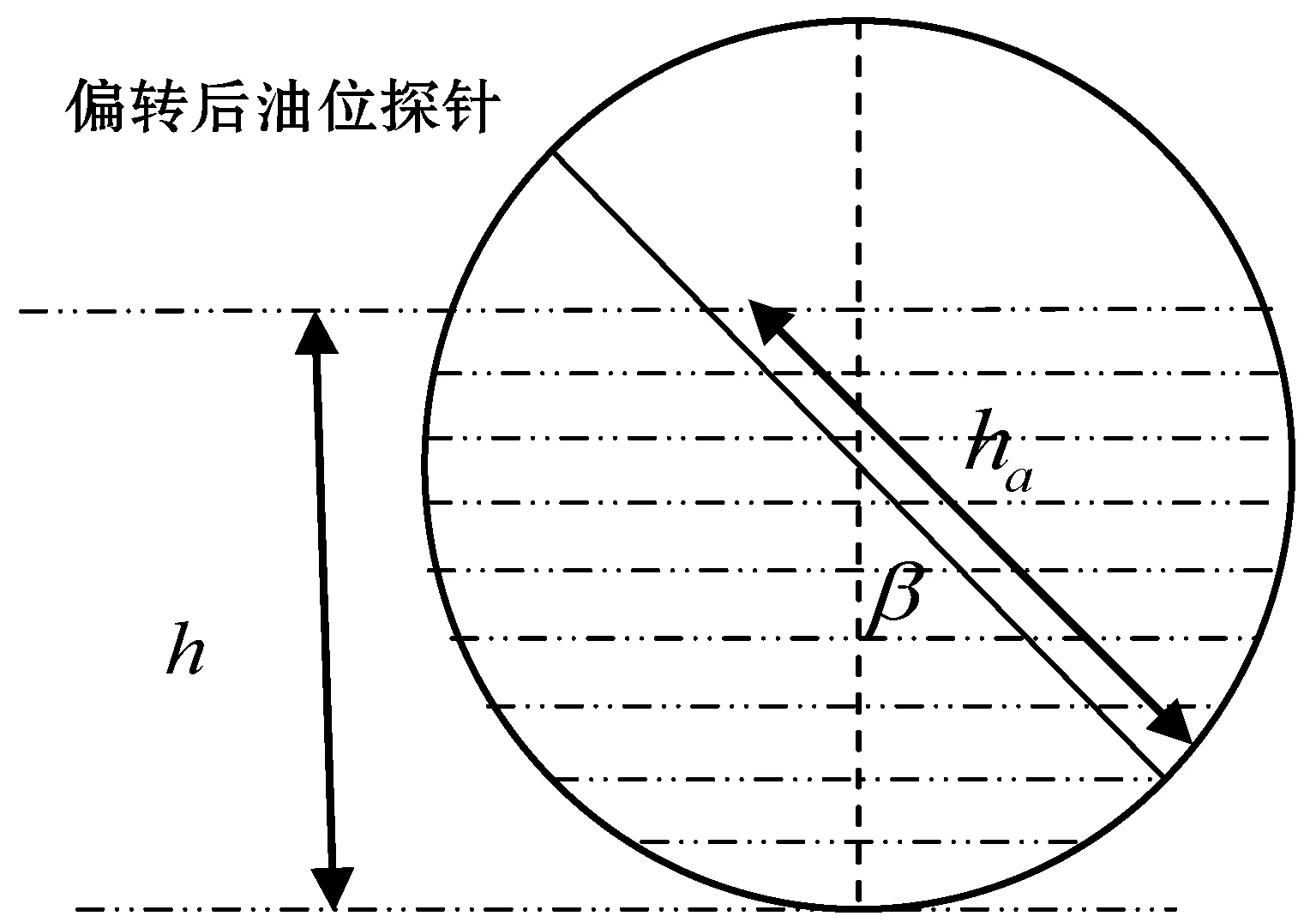
图3 储油罐横向倾斜前后油位探测针

发生横向偏转后,油位探测针所测得实际油位高度ha与未偏转油位h的关系为:

h=R+(ha-R)cosβ

(9)

2 基于模拟退火算法的油罐变位识别

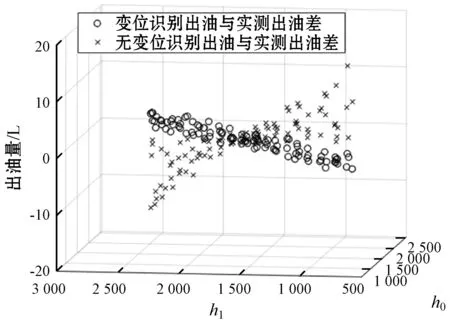
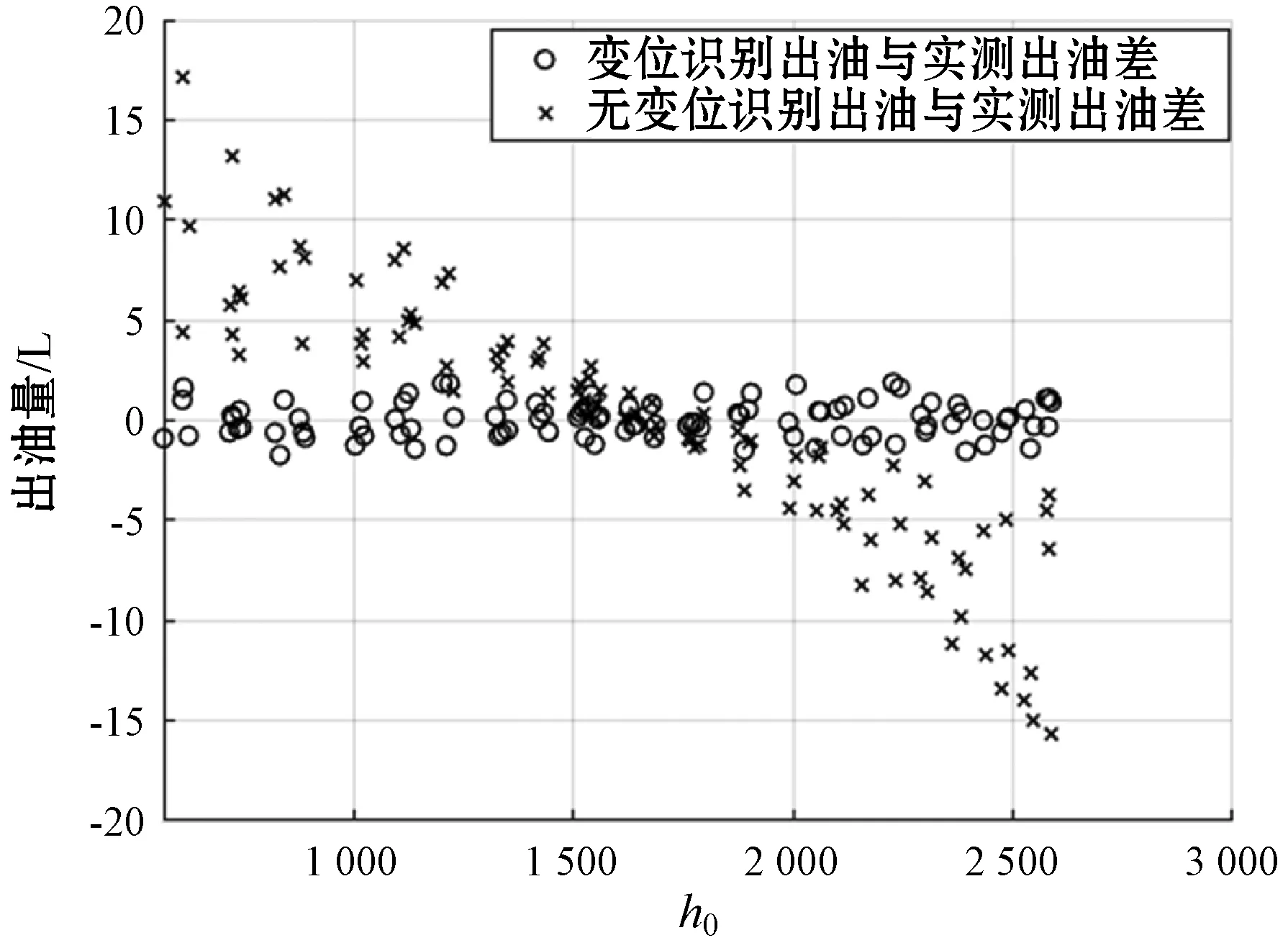
模拟退火算法SA(Simulated Annealing)[12-15]最早是由Metropolis等提出来的一种基于蒙特卡罗思想的随机全局寻优算法,算法来源于物理学中固体物质的退火过程与组合优化间的相似性。在某一初温下,伴随着温度参数的不断下降,利用具有概率突跳性的Metropolis准则在解空间中随机搜索,在局部最优解时以一定概率接受新解并跳出局部最优解,最终趋于全局最优[16],计算量相比于蒙特卡罗法、最小二乘法显著减少。具体而言:在某一温度t下,在当前状态X(n)基础下根据某一指标(梯度下降)产生新状态X(n+1),两个状态对应的能量分别为En和En+1,若En

模拟退火算法流程如图4所示。

图4 模拟退火算法流程

(11)

模拟退火算法中新解的产生流程描述如下:

(1) 随机产生两个N(0,1)的随机数m0和m1;

(2) 计算温度采用率:

(3) 根据解x0产生新解x1:

x1=x0+z×T

(13)

(4) 新解有效性检查,若新解无效,则在解空间内随机产生新解。

求解储油罐的最优变位角,即是求解使目标函数f(x)函数值最小的α角和β角。

3 实验结果分析

设置模拟退火算法的初始温度T0为1 000,退火速率λ等于0.95,外层循环结束条件为循环迭代500次,内层循环抽样稳定准则为循环迭代50次,解空间为0°≤α≤15°且0°≤β≤15°。随机选择文献[17]附件2中的400组实测出油量及油位高度变化的数据对模型做变位识别。退火适应度进化曲线如图5所示。

图5 退火进化曲线

由图5可知,模拟退火算法输出的模型的最优变位角为α=2.133 9、β=4.617 3。

将该变位角代入储油罐油位变化、倾斜角与出油量关系模型矫正模型,随机从剩余实测数据中选择100组数据代入矫正后的出油量数学模型,计算变位识别出油量绝对误差。同时,计算出未做变位识别的出油量数学模型的绝对误差,对比结果如图6所示。

图6 变位识别和无变位识别与实测出油量对照

变位识别与未变位识别模型理论出油量与实测出油量对照图如图7所示。可以看出,所建立数学模型做变位识别矫正后,理论出油量更接近实际出油量。

图7 变位识别与无变位识别对照X-Y图

将模拟退火算法求解出的最优变位角代入倾斜储油罐出油量数学模型,计算油位高度从h1下降到h0的理论出油量,并与实际测量数据和文献[9]中实验结果比较,计算模型出油量与实测加油机出油量相对误差,可以得到如表1所示的结果。

表1 实测出油量与模型出油量对比表

油位从h1下降到h0时,罐容表显示容积变化量即为罐容表显示出油量。根据表1可知,文献[17]中实测罐容表出油量相对误差约为7%,文献[9]中采用遗传算法计算出的出油量相对误差约为15%,BP网络的相对误差约为8%,文献[10]模型的相对误差约为16%,本文出油量模型相对误差约为0.01%。本文所建油位高度变化与出油量的数学模型经模拟退火算法变位识别后,可以很好地反映加油机出油量与油位高度变化的关系。通过出油量与油位高度关系建立的数学模型在相同油位变化下的油量容积变化的误差较大,其中可能存在累积误差、模型误差及出油机误差等。

4 结 语

本文采用定积分的方式建立储油罐油位高度变化量、倾斜角与出油量的数学模型,通过MATLAB、非线性最小二乘法和模拟退火算法求解模型最优变位角。对发生变位后的出油量数学模型做矫正,并利用实测数据检验、文献数据对比分析证明了本文模型和变位识别方式的正确性及实用性和建模方式减少累积误差的优势。储油罐在实际使用过程中,影响出油量与油位变化不匹配的因素还有很多,比如温度、液位计精度等,还需要做更进一步的研究。