基于改进人工势场法的移动机器人路径规划
2023-08-10徐劲力许建宁黄丰云李征瑞
徐劲力 许建宁 黄丰云 李征瑞
(武汉理工大学机电工程学院 湖北 武汉 430070)
0 引 言
路径规划技术在移动机器人领域中是一项尤为重要的技术,是其自主移动完成各种复杂任务的前提,更是所有移动机器人可以进行智能化技术应用分析研究的一切前提。近年来,国内外学者提出一系列算法应用在路径规划研究当中,主要包括人工势场法[1-3]、蚁群算法[4]、遗传分析算法[5]、A*算法[6]、RRT算法[7]等。相比于其他算法,人工势场法比较简单,计算量小,所规划的路径相对较为平坦,但是也存在障碍物附近目标不可达以及陷入局部最小值无法运动等缺陷。为了解决这些问题,国内外学者对其进行了改进:杨凯等[8]通过对斥力场模型进行改进优化,通过设置虚拟目标点解决移动机器人在搜索路径研究过程中可能出现的局部最小值问题;Orozco-Rosas等[9]提出采用遗传算法与人工势场算法融合以此来对人工势场法进行改进,搜索出一条无碰撞的路径;汪四新等[10]通过改进斥力场的人工势场与模糊算法相结合,利用模糊决策系统调整机器人运动,使得规划出的路径平滑;李靖等[11]通过改进人工势场法中的势场模型,去除斥力场,设置动态引力场,在机器人运动过程中不断对引力场进行修正,最后对生成的路径进行平滑;侯翔[12]通过改进人工势场法中的势力场模型,引入指数因子,采用量子遗传算法对规划出的路径进行优化平滑。
本文在现有研究基础上,针对人工势场法应用在移动机器人路径规划领域存在的问题,提出一种改进的人工势场法。通过改进斥力场函数模型,将人工势场法与模拟退火算法融合,并通过路径优化算法规划出一条无碰撞的平滑路径。
1 传统人工势场法
人工势场法是通过在机器人进行运动时建立势力场,并使得在目标点出的合势力为全局最优值。对于移动机器人在二维空间中任意一点q=[xy],传统人工势场法通过在空间中目标点qg=[xgyg]建立引力势场,在各个障碍物qo=[xoyo]处建立斥力势场。在目标点引力Fatt以及障碍物排斥力Freq的作用下,通过两者的合力F以及给定的步长λ0确定了移动机器人下一步的运动方向[13],如图1所示。
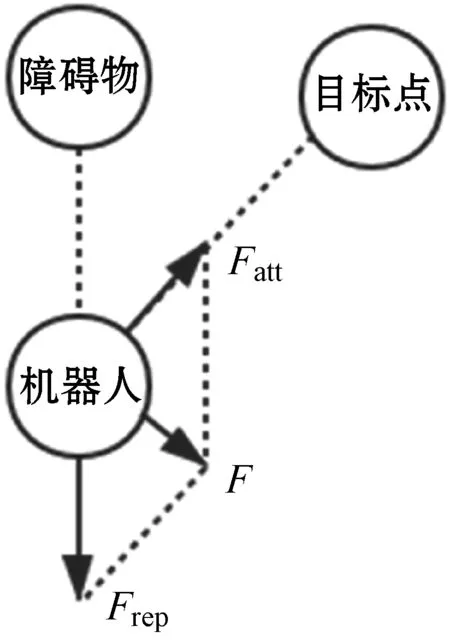
图1 移动机器人受力示意图
传统人工势场法的目标点引力场函数模型如下:
式中:Katt为所述引力势场的增益系数。
对应的引力为:
Fatt(q)=-grad(Uatt(q))=-Katt(q-qg)
(2)
障碍物点处斥力场函数模型如下:
式中:Kreq为所述斥力势场的增益系数;ρ为机器人当前点q与障碍物点qo的直线距离;ρ0为障碍物点影响距离。
对应的斥力为:
Freq(q)=-grad(Ureq(q))=
机器人所受的合势场以及合力为:
U(q)=Uatt(q)+Ureq(q)
(5)
式中:N为障碍物的数目。
2 改进人工势场法
2.1 改进势力场函数
传统人工势场法中,机器人在建立好的势力场中受到障碍物的斥力以及目标的吸引力,两者合力的方向决定了机器人的运动方向。从式(2)、式(4)可以看出,当移动机器人愈靠近目标点(位置在障碍物影响范围内)时,受到的斥力会远远大于引力,机器人无法到达目标点,因此对势场函数模型进行改进,在斥力场函数中引入当前点与目标点的欧氏距离。同时,为减小路径的振荡性,添加最小引力势能。
此时改进引力场函数模型为:
式中:Umin为最小引力势能。
对应的引力为:
Fatt(q)=-grad(Uatt(q))=
改进后的斥力场函数模型如下:
对应的斥力为:
式中:
此时移动机器人的受力如图2所示。
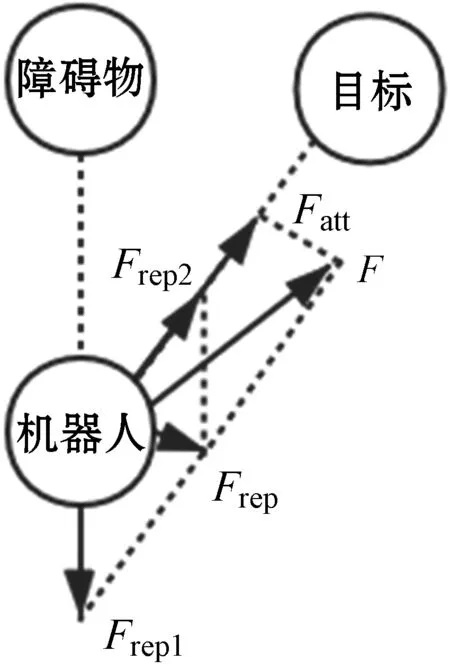
图2 改进斥力场移动机器人受力示意图
2.2 局部最小值问题
为处理采用人工势场法时所出现的局部最小值问题导致机器人不可移动的情况,本文采用变步长的模拟退火算法逃逸当前局部最小点。模拟退火算法是模拟工程中物质退火的算法,当加热后的高温材料温度逐渐冷却时,材料内能逐渐降低,分子逐渐趋向稳定,能够以一定概率跳出当前的局部最小值[14]。算法步骤如下:
步骤1初始化算法中如下设计参数:初始工作温度为T=10,退火速率为α=0.9。
步骤2随机产生新解:在范围内给移动机器人一随机角度θ、步长λ=βλ0,其中β为步长增益系数,判断机器人以该随机角度以及增益后的步长运动后是否与障碍物碰撞,若碰撞,重复步骤2;否则,进行下一步。
步骤3计算随机点的合势能Urand、前一个点的合势能Ubef、势能变化量ΔU=Urand-Ubef。
步骤4采用Metropolis准则,判断是否接受当前随机解,若ΔU<0,则接受当前随机解,否则产生一个随机数r,若exp(-ΔU/T)>r,则接受当前随机解,进行下一步;否则,重复步骤4。
步骤5按照退火策略T=αT更新参数,判断是否跳出局部最小值,若已逃逸,退出模拟退火算法,否则,重复步骤2-步骤4直至逃逸出局部最优解。
3 路径优化算法
3.1 路径优化策略
由于改进人工势场法中获得的路径点存在冗余的路径点与振荡点,当运动到障碍物附近时合力产生突变,生成的路径点存在振荡的情况,生成的路径点在实际中无法应用,因此本文研究提出一种路径优化平滑算法,其步骤描述如下:
步骤1移动机器人通过改进后的人工势场法获得从起始点到目标点的无碰撞路径点序列为Qi(xi,yi),其中J为路径点的总数,初始化空数组LQ。
步骤2设障碍物点为Ci,i∈[0,N],路径起始点A为Qm,m=1,选取路径点的后两个点B为Qn,n=m+2开始,计算点Ci,i∈[0,N]到直线AB的距离,若大于给定距离参数D,则n=n+1,否则判断CA与CB的夹角,若为锐角,则n=n+1,否则,将Qm放入数组LQ中,m=m+1。
步骤3重复步骤2,直至m=J。
步骤4将获得折线路径的拐角左右两条折线上取得中点以及靠近拐点的四等分点,通过四次贝塞尔样条插值进行平滑处理,当对n个顶点进行p次B样条插值时,其曲线方程式为:
式中:P(i)(i=0,1,…,n)为控制点;Ni,p(t)为p次B样条基函数。
3.2 技术路线
至此,改进算法的技术流程如图3所示。当给定起点、目标点、移动步长时,采用改进的人工势场法进行路径规划搜索,通过相应的路径优化策略对已经规划出来的路径进行优化,并在拐点处采用四次贝塞尔曲线进行平滑。
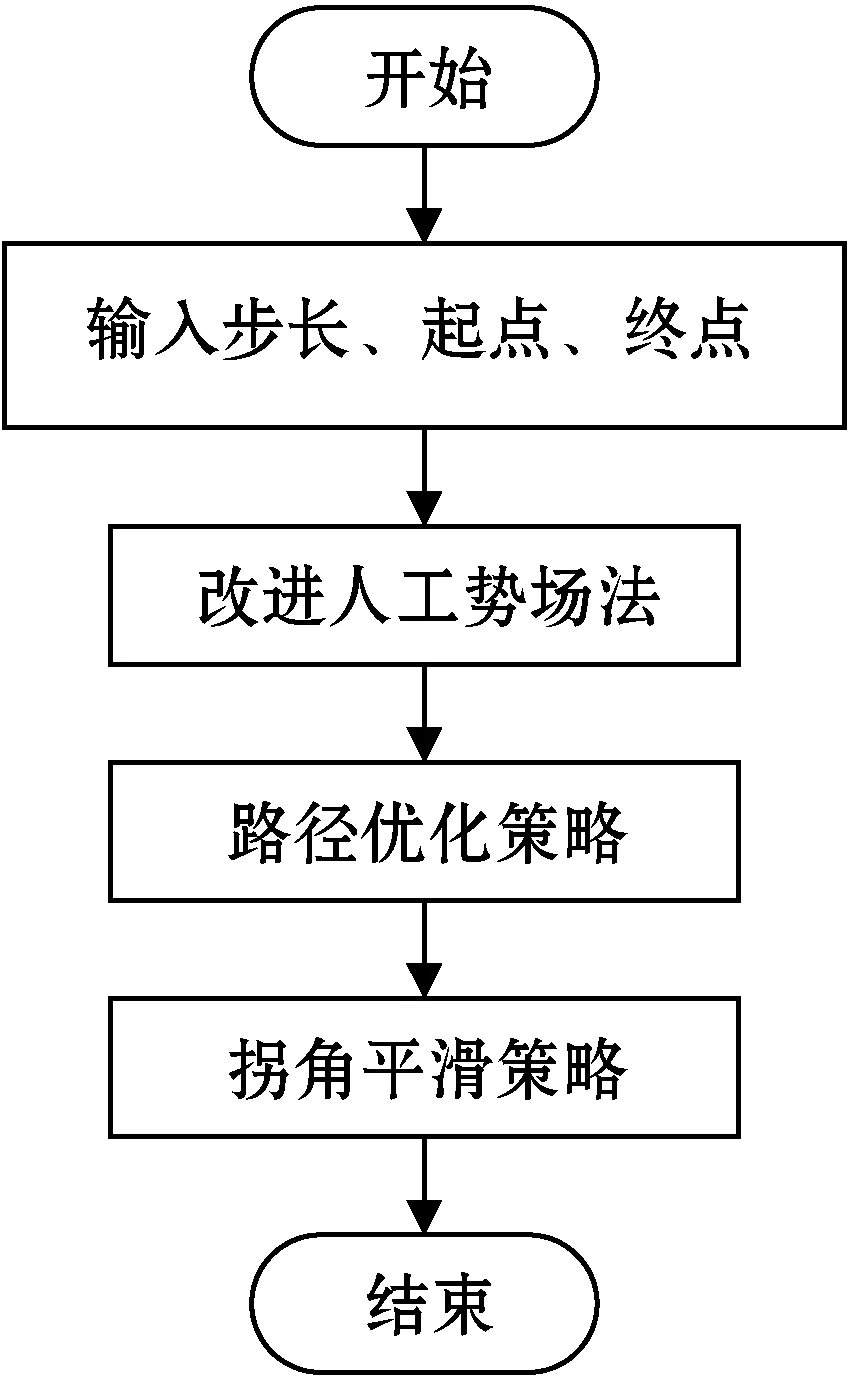
图3 算法技术路线
3.3 实验仿真分析
以在二维空间内的路径搜索为例,以此验证本文算法以及路径平滑策略的有效性。基于MATLAB设置仿真实验,通过机器人的形态特征设置路径平滑距离参数,设置算法参数如表1所示。

表1 算法参数表
在二维空间内设置起点S(0,0)与终点G(10,10),通过圆形模拟静态障碍物。采用传统人工势场法以及本文算法进行模拟仿真在以下三种典型障碍物(平衡点、障碍物附近目标、槽型障碍物)进行模拟仿真,其仿真结果对比分别如图4-图6所示。
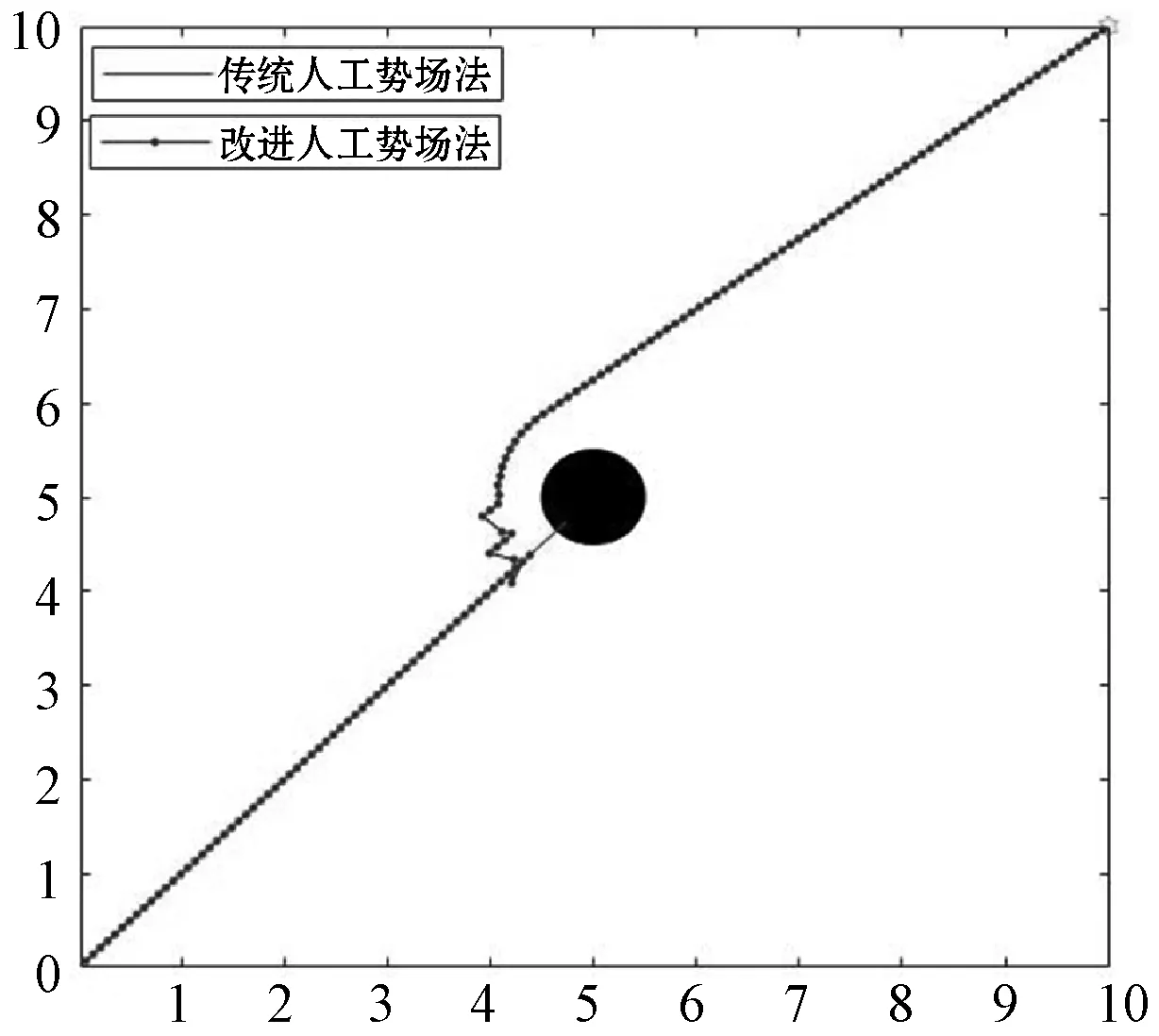
图4 平衡点出仿真对比
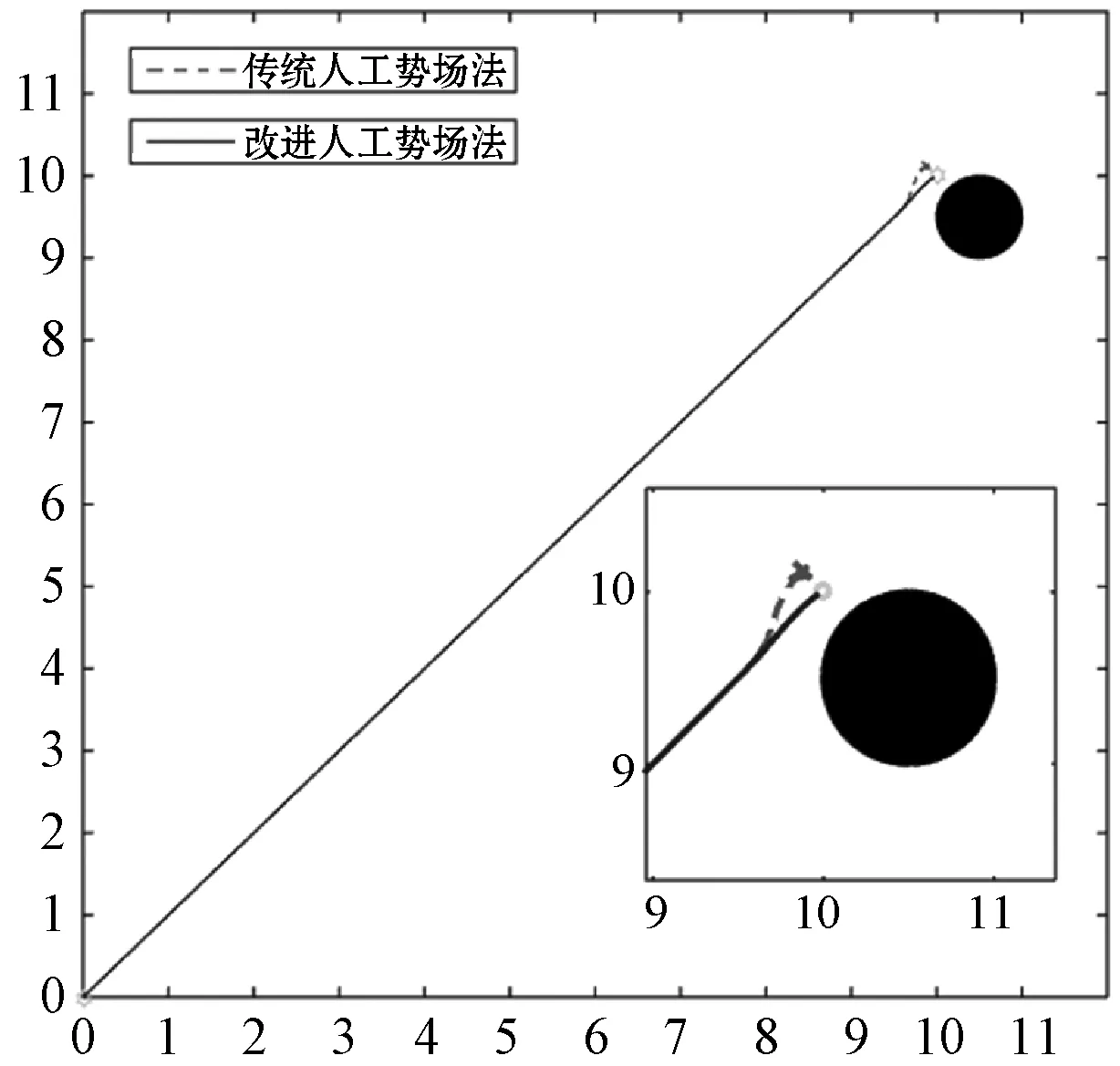
图5 障碍物附近目标不可达

图6 槽型障碍物
可以看出,改进后的算法均能克服传统人工势场法应用到相应典型障碍物情况下无法完成路径规划仿真的缺点。为进一步说明算法的有效性,在复杂障碍物场景下采用传统人工势场法的路径仿真示意图如图7所示。分别采用文献[15]中所提出的算法以及本文算法在复杂障碍物环境中进行仿真分析,得到机器人的路径轨迹,并采用本文提出的路径优化策略将得到的路径节点分别进行路径优化处理。文献[15]所得到的优化前后的路径仿真示意图如图8所示,本文算法所得到的优化前后的路径仿真示意图如图9所示。
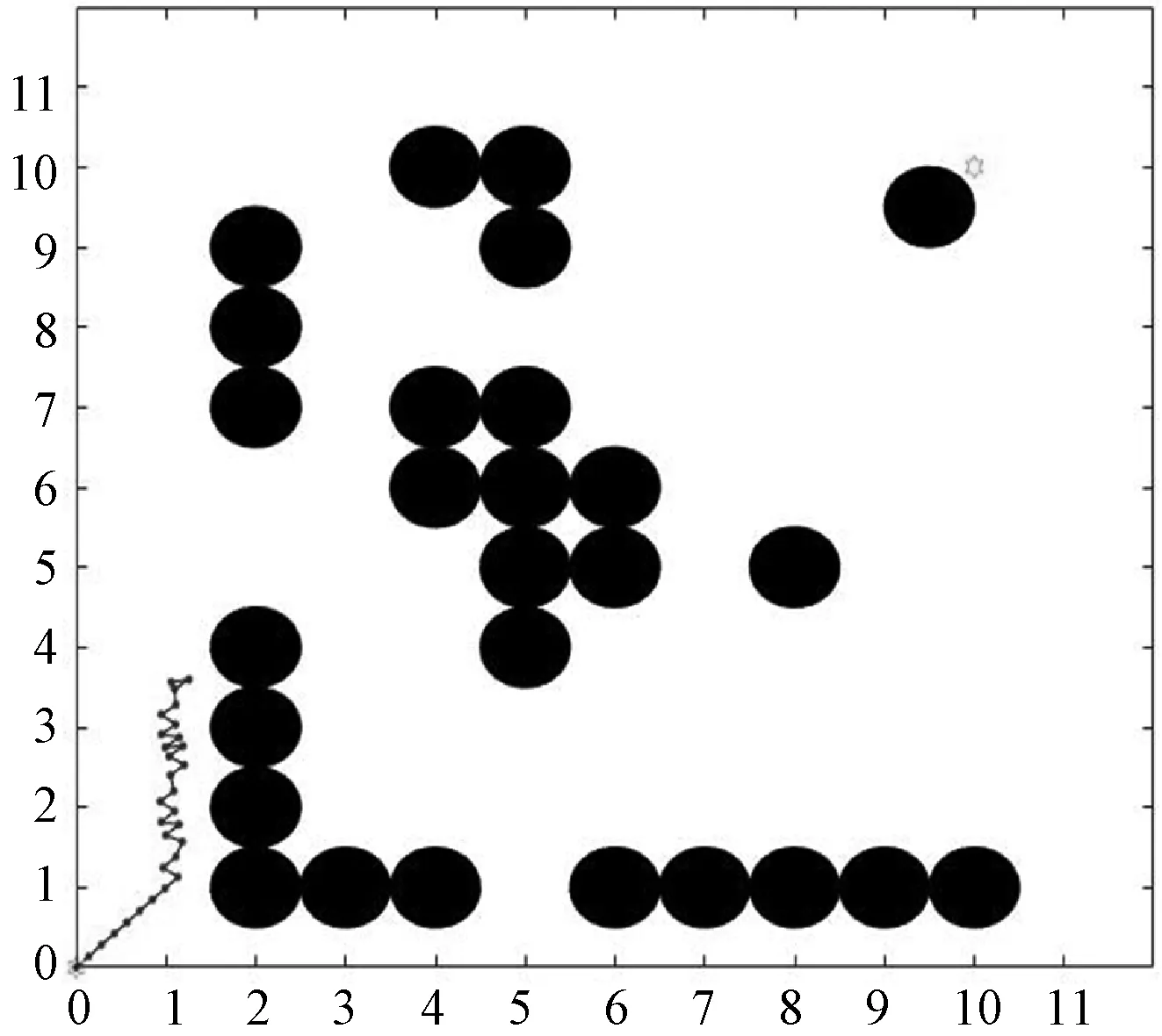
图7 传统人工势场法的路径仿真示意图
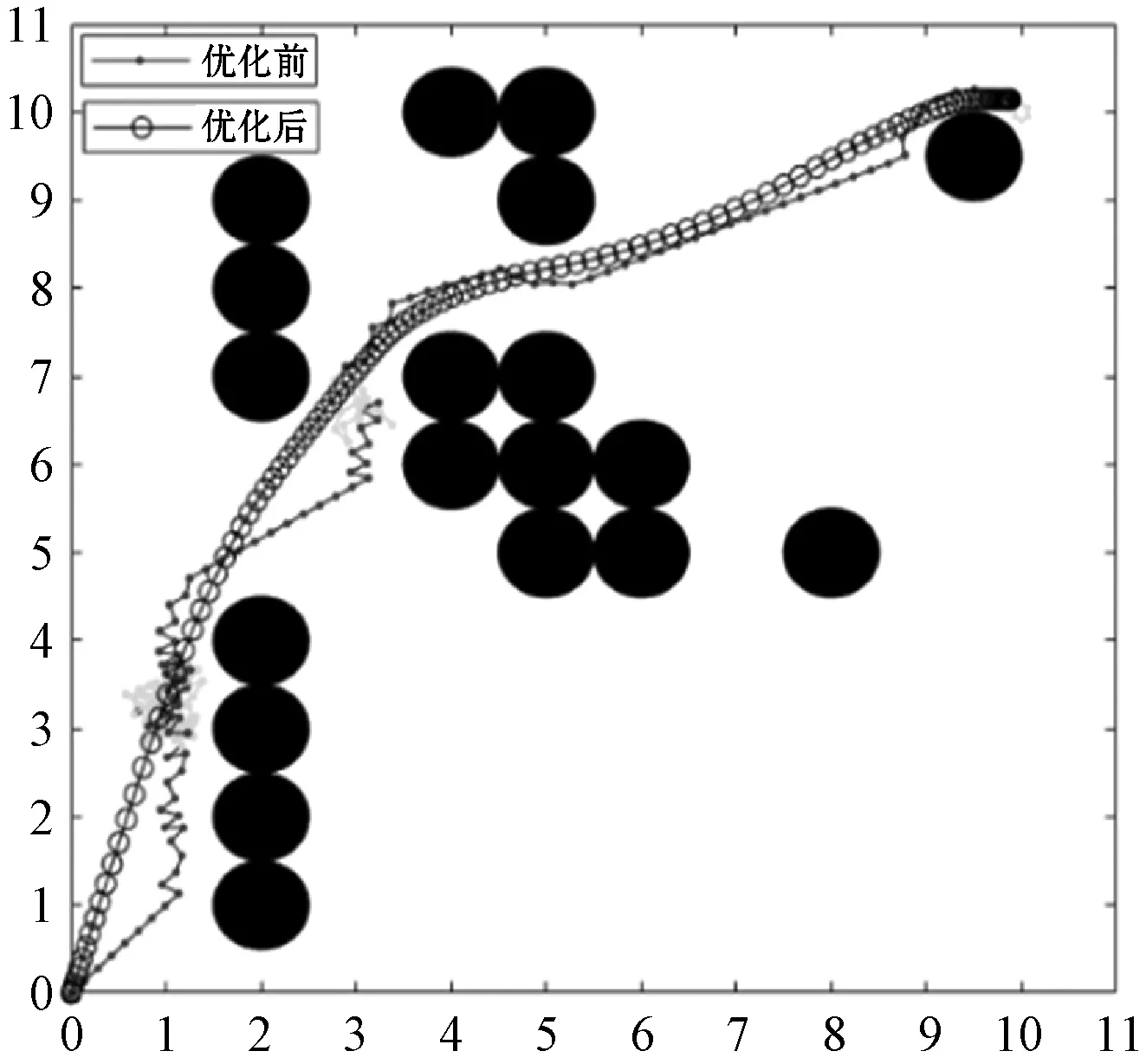
图8 路径优化前后的仿真算法示意图
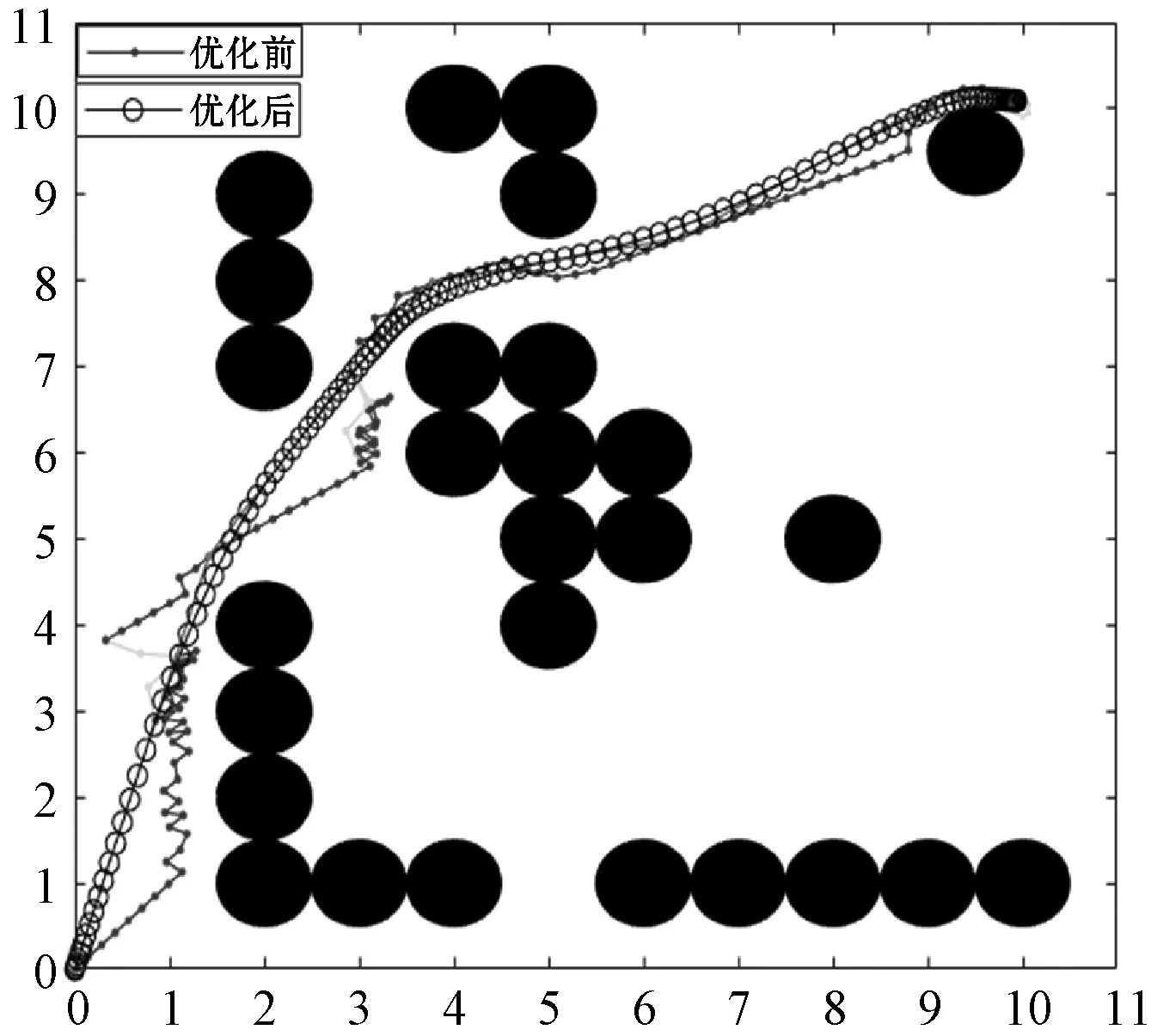
图9 路径优化前后本文算法仿真示意图
从图8可以看出,机器人在当前障碍物环境中无法完成路径轨迹规划。同样的环境中利用文献[15]以及本文算法进行仿真,从图9和图10可以看出,两种算法均能使得移动机器人克服传统人工势场法的缺点,两种算法均能在障碍空间环境内从设置的起点S与终点G之间搜索出一条无碰撞的路径,相比之下本文算法能够更快地逃出局部最小值点,但是在经过路径优化策略处理前,两种算法所得到的路径并不平滑且均存在振荡点。在经过本文提出的路径优化策略进行处理后,两种算法均能消除无碰撞搜索路径的振荡特性,都能得到一条平滑无碰撞的轨迹,表明本文算法的有效性。
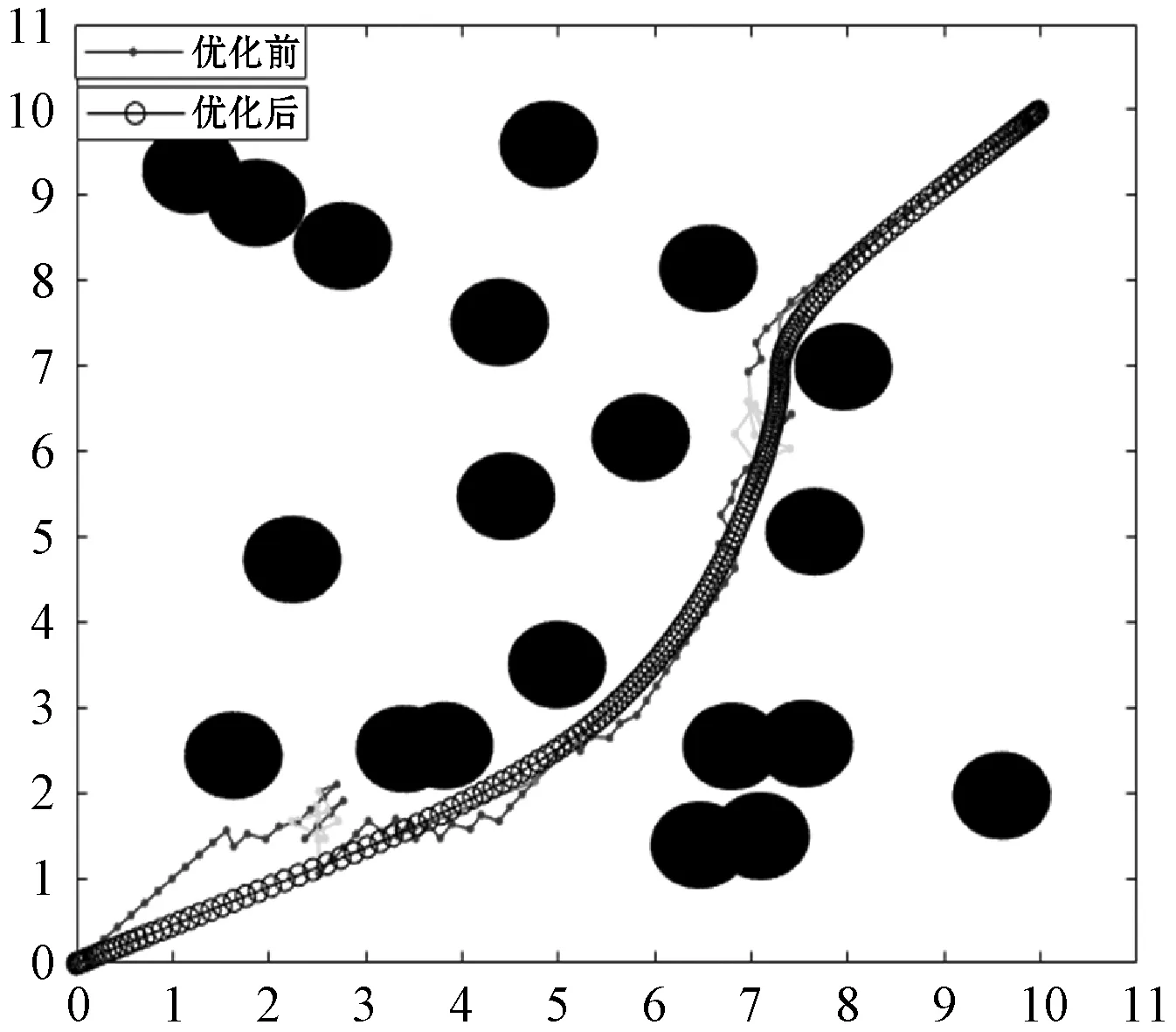
图10 随机障碍物环境1
在保证算法参数相同的情况下,在地图中随机生成障碍物进行多次仿真分析如图10所示,仿真数据如表2所示,改进算法在进行路径优化后相比未进行优化之前平均减少了48.8%,表明了本文算法的有效性。

表2 随机障碍物地图下算法路径优化前后对比
4 结 语
本文结合人工势场法中现有问题,通过对人工势场法的函数模型进行修改,采用模拟退火算法对局部最优问题进行逃离,结合机器人的形态特征,采用提出的路径优化算法去除路径的冗余点与振荡点。并通过MATLAB仿真分析,本文算法能够生成一条平滑的无碰撞路径,仿真结果证明了本文算法的有效性。
