通信测距复合系统中一种改进的时延估计算法
2023-08-10侯艳丽周安敉
侯艳丽 郭 鑫 周安敉
(河北科技大学信息科学与工程学院 河北 石家庄 050026)
0 引 言
通信测距复合系统(简称复合系统)使用软扩频通信方式,把扩频通信和伪码测距任务相结合,使得复合系统在完成扩频通信的同时能够进行测距或者定位,降低了设备的复杂程度和功耗。到达时间差(Time Difference of Arrival,TDOA)[1]估计是保证复合系统完成通信、测距任务的关键,而使用不同的相关运算方法影响着复合系统进行TDOA估计的测距效果。
互相关法作为时延估计常用的求解方法,具有广泛的使用场景[2]。王慧楠[3]利用基于普通相关函数的TDOA检测技术完成了飞行器间通信和相对定位一体化任务,但时延估计的精度有待提高。Knapp等[4]提出了基于广义互相关(Generalized Cross Correlation,GCC)函数的TDOA估计方法,通过选择合适的滤波器对信号进行处理后,可以降低噪声对信号的影响。滕幼平[5]利用广义互相关算法完成复合系统的测距任务,但在低信噪比下的时延估计具有一定的局限性。李一兵等[6]把循环谱知识和平滑相干变换法进行结合,利用组合式时延估计算法进行TDOA检测,改善了复合系统抗干扰能力,但是系统的时延估计性能需要进一步提高。宋颖[7]在广义相关算法的基础上,提出了利用广义循环相关函数进行复合系统的时延估计,但是在低信噪比下,峰值受噪声的影响较大。Stock等[8]利用能量谱估计的改进互相关算法进行复合系统的时延估计,该算法复杂度高、计算量较大。钱隆彦等[9]提出了一种改进的广义二次相关算法,应用在语音信号处理中,在较低的信噪比下具有较好的时延估计性能。
为了改进复合系统在低信噪比下的时延估计性能,本文在文献[5]和文献[9]的基础上,提出一种改进的广义互相关时延估计算法,应用于通信测距复合系统中,该系统可以同时完成通信任务与测距任务,有效地削弱了噪声的影响,增大了主峰和次峰的相对值,在低信噪比下的时延估计性能得到了一定的提高。
1 通信测距复合系统原理
为了保证复合系统可以更有效地同时进行通信任务以及测距任务,将链接序列以及软扩频技术应用到系统当中[10]。首先将串行数据进行串/并转换,成为二进制并行数据,然后按照一定的规则依次选择4个内部序列;再与外部序列复合成为链接序列;最后经调制器调制后发射出去。
在复合系统的接收端,本地序列与接收序列做互相关运算,求得系统的时延估计值,计算得到距离测量值,同时可以得到外部序列的极性以及通信数据。通信测距复合系统工作原理如图1所示。
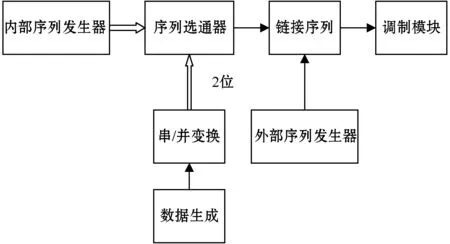
(a) 发射端
2 算法设计
2.1 TDOA信号模型
假设x(t)为已知节点的本地信号,y(t)为已知节点接收到的经由待测节点转发出来的信号,数学表达式为:
x(t)=s(t)+m(t)
(1)
y(t)=s(t-τ0)+n(t)
(2)
式中:s(t)为待传输的信号;s(t-τ0)为待测节点转发后接收到的信号;m(t)、n(t)则分别表示本地环境和信道环境中的噪声。
复合系统的测距任务是通过求得本地序列与接收序列的相位差延时τ0,再按照式(3)计算TDOA,最后根据式(4)求得待测节点和已知节点的距离。
TDOA=τ0·Tc-Tz-Tj
(3)
式中:TDOA表示到达时间差;L表示待测节点与已知节点的距离;τ0为相位差;Tc表示码元宽度;C表示光速,C=3.0×108m/s;Tz表示待测节点变频转发时间;Tj表示到达时间差求解的处理时间。
2.2 广义互相关时延估计算法
基于相关函数的时延估计算法较多,现有的通信测距复合系统中主要采用普通互相关算法、广义互相关算法、循环相关算法等,其中,循环相关算法的性能最优,但计算量较大,综合考虑到算法的性能以及运算的复杂性,本文对广义互相关算法进行改进。广义互相关算法通过选取不同的加权函数对信号进行滤波,从而有效地抑制噪声干扰[11]。最后对加权处理后的功率谱密度函数进行傅里叶逆变换,从而得到广义互相关函数,求得复合系统的TDOA估计值。算法工作原理如图2所示。
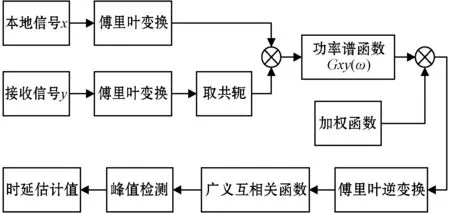
图2 广义互相关算法流程
2.3 改进的广义互相关时延估计算法
在低信噪比条件下,广义互相关算法的抗噪声性能有限,易受噪声或干扰的影响,且经过相关函数运算后的峰值不明显,复合系统的测距误差较大[12]。针对这一问题,本文在此算法的基础上进行了改进,首先对本地信号x(t)和接收信号y(t)做互相关运算,把相关函数做指数运算,再乘以加权函数,削弱噪声的干扰,然后把傅里叶逆变换得到的相关函数做高次方运算,增大主峰和次峰的相对值,使得峰值更加突出,最后进行TDOA检测估计。算法工作原理如图3所示。

图3 改进的广义互相关算法流程
对x(t)和y(t)做互相关运算可得:
Ryx(τ)=E[y(t+τ)·x(t)]=
E[(s(t+τ-τ0)+n(t+τ))·(s(t)+m(t))]=
E[s(t+τ-τ0)·s(t)]+E[s(t+τ-τ0)·m(t)]+
E[s(t)·n(t+τ)]+E[n(t+τ)·m(t)]=
Rs(τ-τ0)+Rsm(τ-τ0)+Rsn(-τ)+Rnm(τ)
(5)
式中:Rs(τ-τ0)为本地信号和接收信号的相关函数;Rms(τ-τ0)为接收信号和本地噪声的相关函数;Rsn(τ)为接收信号和信道环境中噪声的相关函数;Rmn(τ)为本地噪声和信道环境中噪声的相关函数。
假设干扰或噪声之间以及与信号之间互不相关,到达序列和本地序列的相关函数化简为:
Ryx(τ)=Rs(τ-τ0)
(6)
由相关函数性质得到,当τ=τ0时,Rs(τ-τ0)存在极大值。
根据维纳-欣钦定理[13-14],广义互相关函数表达式为:

(7)
式中:φxy(ω)为广义加权函数;Gxy(ω)为x(t)、y(t)的互功率谱密度函数[15]。
本文采用平滑相干加权函数(SCOT):
式中:Gx(ω)、Gy(ω)分别为x(t)、y(t)的自功率谱密度函数。当信噪比较大时,平滑相干法对噪声的抑制能力较强,能够减少信号波动对TDOA估计的影响[16-17]。
改进算法中指数运算公式如下:
p=[Ryx(τ)](k1c+1)
(9)
q=[l]k2(k1c+1)
(10)
式中:P为相关函数指数运算的结果;c为信噪比SNR,单位为dB;l为傅里叶逆变换后的相关函数;q为傅里叶逆变换指数运算的结果;k1、k2为待确定的参数,k1的取值决定了信号和噪声压缩的倍数,k2的取值决定了相关函数的峰值和算法的复杂度。由于参数的取值直接影响到了算法的性能及系统的时延估计精度,故本文对以上参数进行了分析和多次测试。
为了削弱低信噪比下噪声对信号的干扰,k1应取任意小数。在式(9)中,当SNR为0时,指数部分等于1,结果是相关函数本身;当SNR小于0时,可同比例压缩信号与噪声的幅度;当SNR大于0时,相关函数能够看作平方运算。因此,为了使复合系统工作在更低的信噪比下,同时减少噪声对信号的影响,本实验中取k1=0.001。
式(10)对傅里叶逆变换后的相关函数进行高次方运算,以增大主峰与次峰的相对值,k2应取正整数。当k2为偶数时,得到的互相关峰值为正数,而为了保证时延估计结果能够体现出外部序列的正、负两个极性,k2应取奇数,且k2的值越大,算法的复杂度越高。通过对k2进行多次的实验分析,当k2取值为3、5、7、9时,复合系统的时延估计性能较好。因此,为了提高运算速度,同时判断出外部序列的组成,本实验中取k2=3。
3 仿真及结果分析
3.1 仿真参数设置
在MATLAB平台上建立复合系统的到达时间差估计模型,假设信道是高斯白噪声信道,信噪比为-15~10 dB,采用BPSK调制,信号频率为15 MHz,载波频率为150 MHz。复合系统采用链接序列及软扩频技术,设信息码长度为8位,链接序列生成规则表如表1所示。内部序列由4个相关特性良好的mW序列(5阶m序列和8阶Walsh序列的复合)组成,本实验选择mW1、mW3、mW5、mW6序列,外部序列为5阶m序列。设系统的测距精度为10 m,即系统的测距误差是30 m。假设复合系统每个码片周期采样8个点,接收信号延迟4 000个采样码元。
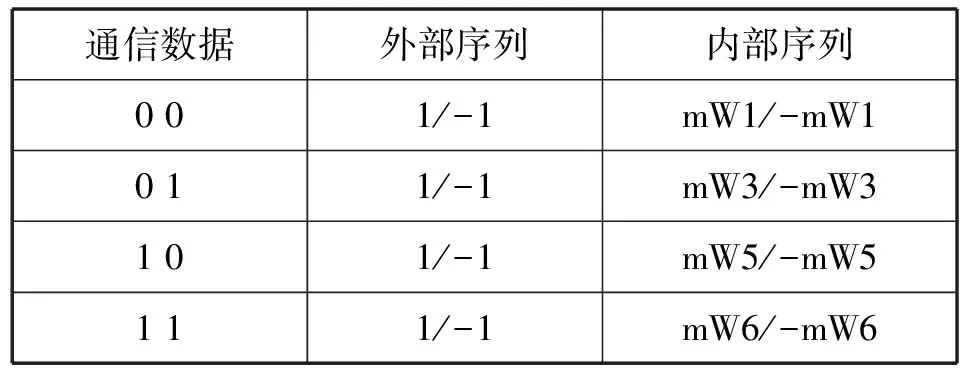
表1 链接序列生成规则表
3.2 系统测距性能分析
对于通信测距复合系统的TDOA时延估计,可以根据互相关函数峰值出现的时刻进行判断。为了验证本文算法的时延估计性能,对改进的时延估计算法进行仿真,并且和广义互相关算法进行比较。
当SNR为5 dB时,仿真结果如图4所示。

(a) 广义互相关算法
可以看出,两种算法都能够得到准确的时延估计值,同时,改进的广义互相关算法的抗噪声性能更好。
当SNR为-15 dB时,仿真结果如图5所示。

(a) 广义互相关算法
可以看出,在SNR为-15 dB下,基于广义互相关算法的TDOA时延估计性能较差,已经不能正确地估计出时延值;而改进的广义互相关算法能够得到正确的时延估计值,且TDOA估计结果的峰值更加突出,更容易进行识别与捕获,在较低的信噪比下具有明显的优势。
为了进一步验证改进的时延估计算法在低信噪比下的测距性能,进行20组仿真实验,SNR为-10 dB,到达时间差延迟为12 000个采样码元,根据式(1)和式(2)计算得到距离测量值为15 000 m。其他参数设置同3.1节。两种算法的平均距离测量值和测距误差如表2所示。

表2 两种算法的测距性能表
由表2可知,改进的时延估计算法与广义互相关算法相比较,得到的距离测量值更加地接近理论计算值,测距误差较小,且满足系统对测距误差的要求,可以较好地完成测距。
3.3 系统通信性能分析
通信测距复合系统的内部序列由4个相关特性良好的伪随机序列组成,接收端需要4个内部序列相关器进行相关处理。系统随机产生8位二进制通信数据为10010011,为了验证改进算法的通信性能,将接收信号经过内部序列相关器,仿真结果如图6所示。根据4个相关器在不同时刻输出峰值的顺序能够判断出内部序列和外部序列的组成,恢复通信数据。

图6 接收信号经过内部序列相关器结果
在表1的基础上,根据图7仿真结果可知,复合系统传输的内部序列编号依次为mW5、mW3、mW1、mW6,对应的8位二进制通信数据为10010011,与发射端生成的通信数据结果一致,说明通信数据恢复正确。
4 结 语
本文提出一种基于改进的广义互相关函数算法的通信测距复合系统,将相关函数做指数运算,在频域内给予一定的加权,然后把经过傅里叶逆变换得到的相关函数做高次方运算,最后进行时延估计,有效地减少了噪声的影响,增大了主峰和次峰的相对值。通过MATLAB仿真结果可以看出,该复合系统能够正确地恢复出通信数据,同时完成测距任务,且在低信噪比下的测距误差较小,具有更好的时延估计效果。
