基于情境感知注意机制的出租车需求深度学习预测模型
2023-08-10樊云阁吕玉辉韩红旗
樊云阁 吕玉辉 韩红旗
1(河南农业职业学院信息工程学院 河南 郑州 451450) 2(洛阳理工学院计算机学院 河南 洛阳 471023) 3(中国科学技术信息研究所 北京 100038)
0 引 言
城市出租车作为一种绿色公共交通工具,为广大乘客提供舒适、便捷的服务[1]。然而,出租汽车服务中存在的一个主要问题是搭乘服务供给与乘客需求之间的时空平衡。为了保持城市道路交通供给与乘客需求的平衡,准确预测城市出租车需求具有重要意义[2]。
出租车需求与包括道路网、兴趣点、气象及假日资料等数据之间的相关性已经得到了很好的研究,但是,要做出准确的预测还存在一些挑战[3]。首先,出租车需求具有高度的动态性,即随着时间的推移变化迅速且有一定的随机性;第二,城市不同功能区的出租车需求变化趋势存在显著差异;第三,出租车需求受一些外部因素的影响较大,如景点、天气状况和节假日等[4]。
为了预测出租车需求,学者们提出了一系列方法。例如,利用自回归综合移动平均(ARIMA)及其改进方法,将出租车需求预测问题建模为时间序列预测[5]。文献[6]提出一个具有高维特征的统一线性回归模型来预测各地区的出租车需求。由于缺乏非线性建模能力,这些方法通常预测精度较低。近年来,深层神经网络(DNN)被引入到出租车需求预测中,它提取了复杂的时空相关性,并利用外部因素辅助预测。例如,文献[7]提出了一种基于长短时记忆(LSTM)网络的序列学习框架,利用瞬时空间相关性,将卷积运算与LSTM相结合。文献[8]同时提取空间相关性和时间相关性,利用外部因素进一步提高预测精度。Tang等[9]利用模型训练过程中学习到的固定参数矩阵,尝试将时空相关性和外部因素结合起来。以上现有研究成果都局限于将不同的时空特征和外部因素结合在一起,这是因为在没有考虑到情景信息的影响下对参数设置了固定的值,仅限于通过理想化的出租车需求多视角特征以及单纯外部因素的情境感知情形下,才可以简单地确定网络中的可学习参数,所以并未充分挖掘数据中蕴含的信息,并且适用范围也有限。
为解决上述问题,本文提出一种基于改进递归神经网络的情境感知注意预测算法,用于预测城市出租车需求。通过纽约市的多个实际数据集实验验证了本文方法能够有效提升预测精度,方法更具一般性。
1 问题描述
定义1(道路网络) 市区的路网由一组路段组成,每个路段都有两个终点,即十字路口的交叉点相关联,并通过共享相同的终点与其他路段相连,所有路段均以图形格式构成道路网络。
为了在空间和时间维度上更完善地描述细粒度的出租车需求,将时间离散化为一组等间隔的时间段,用τ={t1,t2,…,tτ,…}表示,其中tτ表示当前时间段。还根据其道路网络将整个市区划分为不相连的区域。每个区域都是被多个路段包围的不规则多边形。区域集由R={r1,r2,…,rN}表示,其中N代表第几个区域。根据时间段和区域的定义,进一步提出了出租车的细粒度需求的正式定义如下。
定义2(出租车需求) 使用Xn,τ表示在时间段为tτ∈τ、区域为rn∈R的出租车乘客人数。然后,将在时间段tτ的出租车需求定义为Xτ=[X1,τ,X2,τ,…,XN,τ]。
定义3(出租车行程记录) 用{tr}表示一组出租车历史行程记录。每个记录tr包含上下车的位置和具体时间,可以用元组tr=(tr.pl,tr.pt,tr.dl,tr.dt)表示。在此元组中,用纬度和经度表示上车地点tr.pl和下车地点tr.dl,而用年月日、小时和分钟的形式表示具体的上车时间tr.pt和下车时间tr.dt。
为了预测未来的出租车需求,首先从定义3中的历史出租车行程记录中提取出历史时间段的出租车需求。给定一个市区出租车行程记录的数据集,可以根据某区域rn和某时间点tτ的历史出租车需求,近似估计得到出租车的乘客数量,公式如下:
Xn,τ=|{tr|tr.pl∈rn∧tr.pt∈tτ}|
(1)
式中:tr.pl∈rn和tr.pt∈tτ分别代表记录tr在区域rn与时间段tτ的具体乘车地点和乘车时间;函数|·|表示集合的基数。
定义4(兴趣点) 兴趣点(POI)即位于市区的场所,如购物中心。每个兴趣点pi与一个位置pi.l和一个范畴pi.c∈C相关联,C表示类别集。
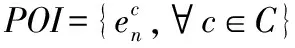
(2)
式中:pi.l∈rn表示POI的pi位于区域rn。此外,还为每个区域rn定义了一组邻域集合rn.neig,该区域由相邻区域组成。
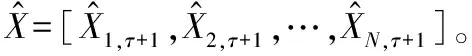
2 数据描述与分析
2.1 道路网络数据
本文采用了2016年调查的纽约市道路网络的数据集[10],该数据集包含87 898个十字路口和91 649个路段。每个交叉点都是矢量,按其纬度和经度定位。利用文献[11]中提出的基于形态学的地图分割方法,根据路网将纽约市的整个区域划分为972个不相交的区域。
2.2 出租车行程数据
纽约市的出租车和轿车委员会已经开放了纽约市出租车出行记录的数据集[12],其中包含出租车的详细驾驶信息,例如每辆出租车的上下车地点和具体时间。2016年1月1日至2016年6月30日(130个工作日和52个周末)的出租车行程数据记录了87 866 988次旅行,覆盖纽约市的972个地区。
图1分别描绘了三月和四月各地区工作日和周末的出租车平均需求量。一个地区的颜色越深,该地区的出租车需求就越多。可以发现,不同地区的出租车需求之间存在严重的不平衡。此外,工作日和周末的出租车需求有显著差异。

(a) 工作日 (b) 周末 图1 纽约市平均出租车需求量
图2和图3分别显示了短期(一天)和长期(一周)出租车需求的周期性,其中分别绘制了格林威治村和中央公园两个地区的出租车需求。
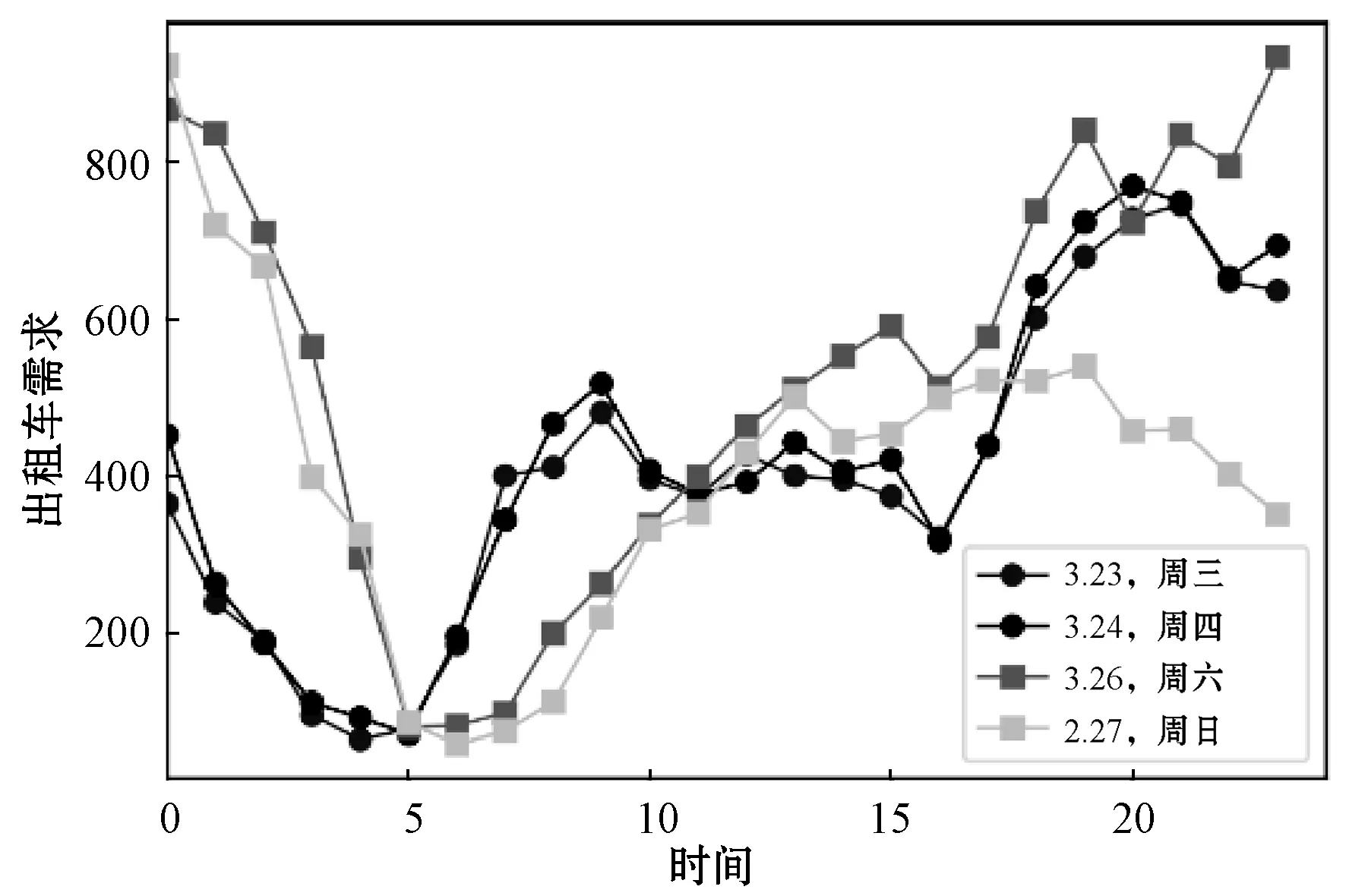
(a) 格林威治村
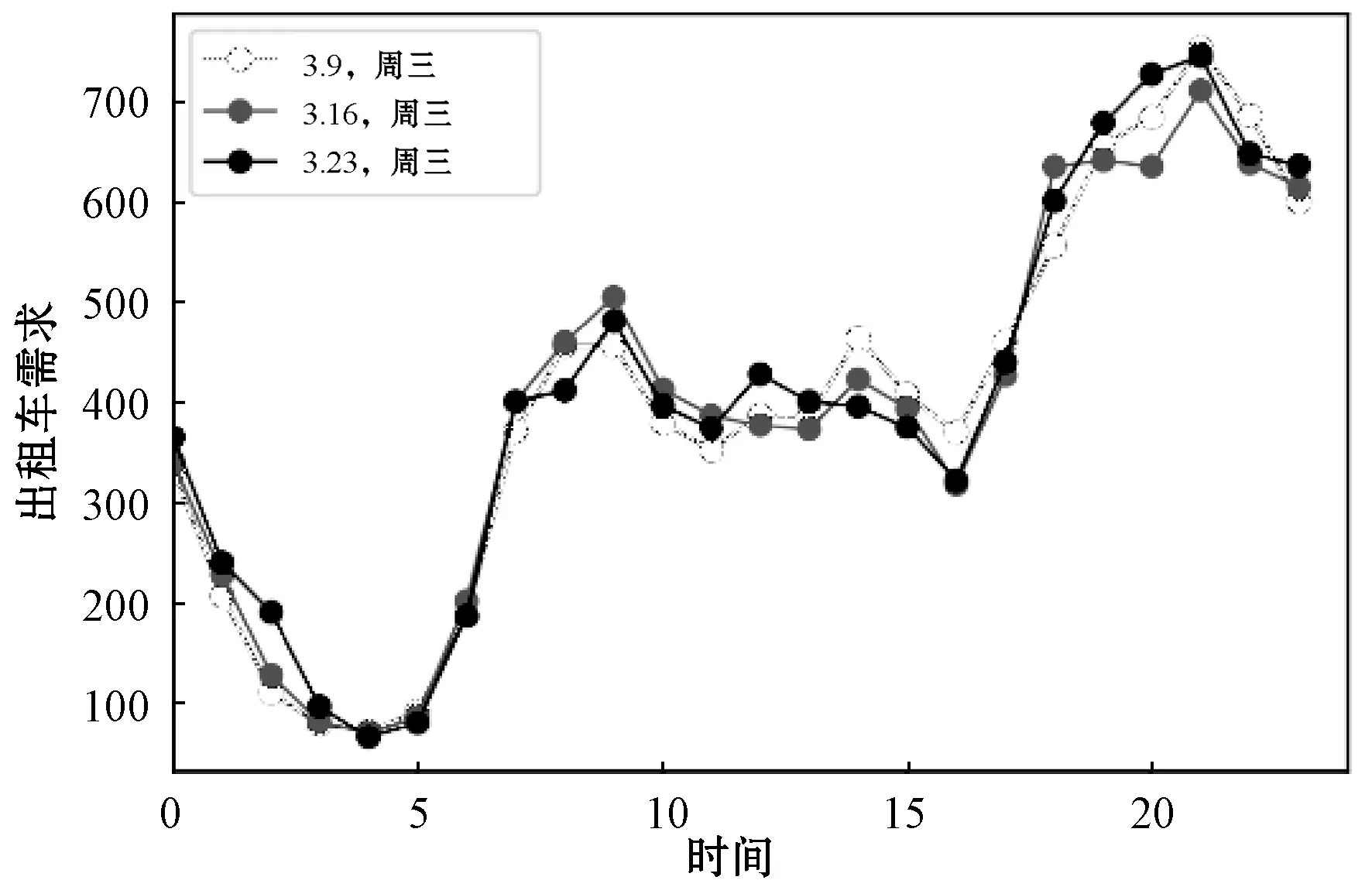
(a) 格林威治村
尤其是图2显示了三月中不同的四天中(包含两个工作日和两个周末)每小时出租车需求变化。不难发现,周三和周四两个地区的出租车需求具有相似的变化趋势,而周六和周日也是如此。这表明每个地区的出租车需求在短期内具有较强的周期性。此外,由于人们在工作日和周末的出行方式不同,各地区在工作日和周末的周期变化趋势显然也不一样。
同样,从图3中可以看出,由于两个地区每周三出租车需求的变化趋势相似,因此出租车需求在长期内具有较强的周期性。短期和长期周期性的存在可以帮助预测未来每个地区的出租车需求。
2.3 POI数据
POI中包含的信息,如一个区域中不同类别的POI数量,反映了该区域的社会功能,这也与出租车需求相关。在纽约使用了一个有670 916个POI的POI数据集,分为16个不同的类别,如表1所示。

表1 兴趣点的类别
图4(a)和图4(b)分别描绘了艺术与娱乐类POI的地理分布以及周六中午12点至下午6点的出租车需求。可以发现,在某些地区(虚线圆圈标出部分),某些类别的POI数量与某些时期的出租车需求有很强的相关性。
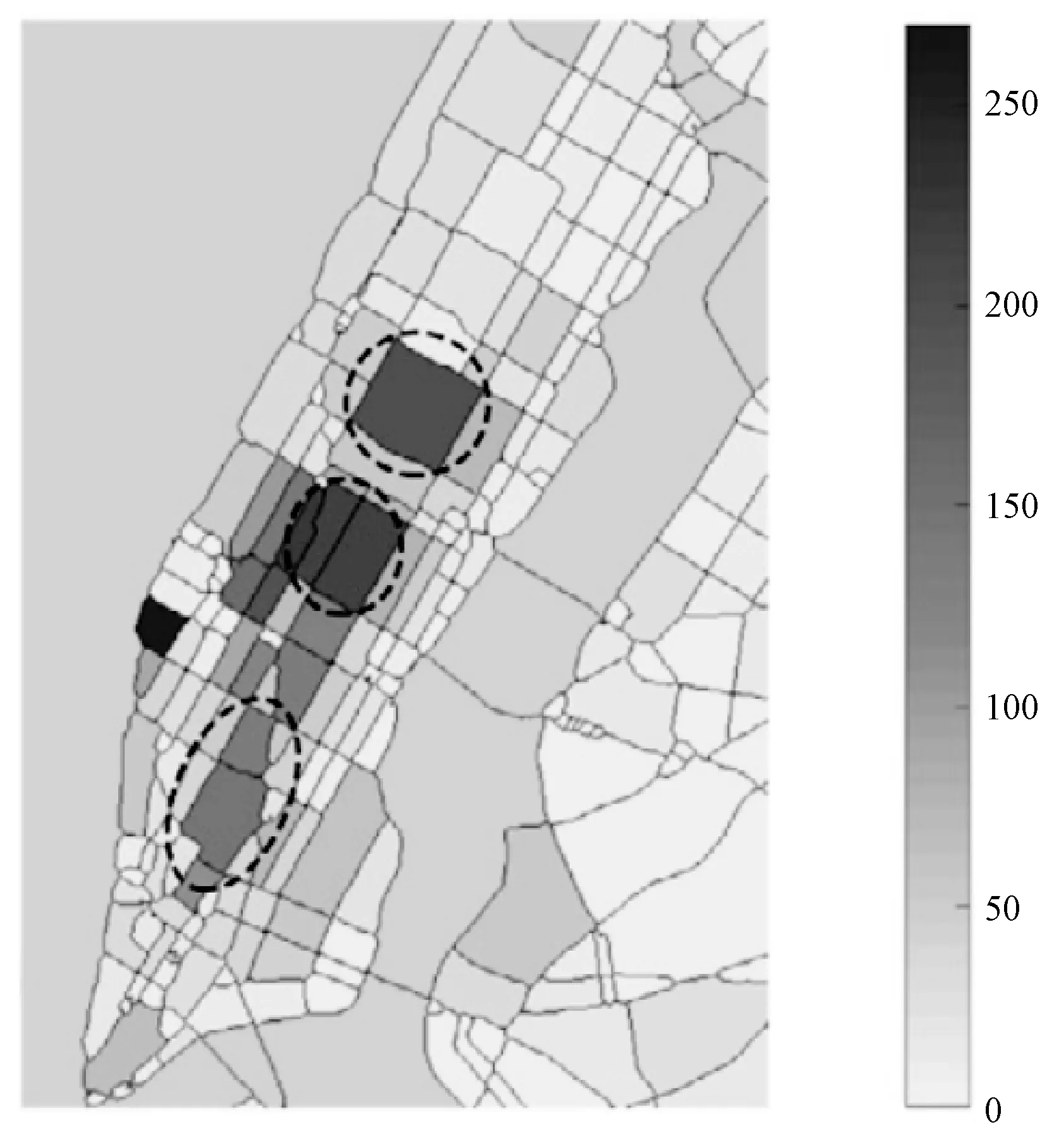
(a) POI:艺术娱乐
为了进一步探索出租车需求与POI之间的关系,以两个标志性建筑为例:哥伦比亚大学(位于347号区域)和纽约城市大学(位于382号区域)。将POI的比例分为六个类别,即不同企业间对比、专业人员和服务、家乡和家庭、食品与餐饮、教育、购物,跟踪出租车需求在一天内的变化如图5所示。可以发现这两个地标具有相似的POI分布和相似的出租车需求变化趋势。通过这种观察,可以利用POI数据来辅助预测出租车需求。

(a) POI比例
2.4 气象和假期数据
除POI之外,出租车需求还受到其他外部因素的影响,例如天气状况和节假日。还在工作中使用了2016年1月1日至2016年6月30日的气象记录数据集,其中包含每六小时记录的天气状况,例如,晴天和阴雨、温度、风速和湿度等信息。
图6描绘了纽约市在不同天气下一天的总体出租车需求,这表明天气状况对出租车需求有很大的影响。特别地,从图6(a)中可以发现,暴风雪后出租车需求显著减少。相反,图6(b)显示了当早上7点到9点下雨时,更多的人会选择乘坐出租车。
3 模型设计
3.1 CACRNN模型概述
图7提供了前文提出的深度神经网络模型的概述,该模型包含四个模块。

图7 深度神经网络模型结构
(1) 实时时空模块。该模块由一系列局部卷积(LC)层和门控循环单元(GRU)组成,这两个层用于在封闭时段内提取出租车需求的时空相关性。特别地,它以o个连续时间段中的出租车需求为输入,由Yi=[Xτ+1-0,Xτ+2-0,…,Xτ]∈R0×N表示,并预测出下一个时间段fl∈Ro×N中出租车需求。
(2) 短期周期模块。该模块根据短期周期的出租车需求进行预测。通过GRU来学习短期周期性,以p为周期性时段中的出租车需求序列、间隔Δs作为输入,即Ys=[Xτ+1-pΔs,Xτ+1-(p-1)Δs,…,Xτ+1-Δs]∈Rp×N。此外,该模块还考虑了一些外部因素,如天气和假日对周期性的影响。将tτ中的外部因素的特征表示为向量uτ∈Rl×ω,并将其与出租车需求连接起来作为GRU的输入。在此基础上,预测出了出租车需求fs∈Rl×N。
(3) 长期周期模块。该模块绘制了长期(如几周)周期性模式的出租车需求。与最后一个模块类似,将出租车需求序列Yl=[Xτ+1-qΔl,Xτ+1-(q-1)Δl,…,Xτ+1-Δl]∈Rq×N与外部因素的特征相结合输入GRU,并预测出时刻tτ+1处的出租车需求,用fl∈Rl×N表示。
(4) 情景感知注意模块。利用此模块将上述模块的输出合并到最终的出租车需求预测中,这是一种新的尝试。特别地,此模块可以根据天气信息、时刻索引和区域功能等上下文信息,为每个区域的预测分配不同的权重。
3.2 实时时空模块
该模块的结构基于局部卷积层和GRU,用于提取区域内的潜在空间相关性和特定周期内的时间相关性。

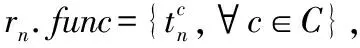
(3)
然后,基于rn和rm的函数向量,计算了它们之间的函数相似性。特别使用了两个向量的加权余弦值来度量相似度,即:
(4)
式中:A(·)表示给定区域的面积。式(4)表明,在出租车需求预测中,POI密度较高的区域对其功能相似区域的影响更大。

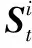
(5)
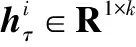
3.3 短期/长期周期性模块
这两个模块分别对出租车需求的短、长期周期性进行预测。如图8所示,它们共享一个基于GRU的结构,以出租车需求和外部因素特征的组合作为输入。

图8 感知机网络结构
时间维度上的外部因素,如天气状况和节假日、周末,对出租车需求的周期性有很大影响。例如,通过调查发现,周末或节假日出租车需求的每小时变化与工作日有显著差异。此外,雨天和晴天出租车需求高峰时段也不同。为了捕捉外部因素的特征,采用了嵌入方法将这些因素在每个时刻的值转换为外部特征向量[13],用ut表示。这种嵌入方法被广泛用于将分类值映射到低维向量。
然后,将出租车需求序列与相应时间内的外部特征向量串联起来作为GRU的输入,并通过FC层将输出转化为下一时间段内出租车需求的预测。短期周期模块预测结果的公式定义如下:
fs=FC(GRU(Xτ+1-pΔs⊕uτ+1-pΔs,
Xτ+1-(p-1)Δs⊕uτ+1-(p-1)Δs,…,Xτ+1-Δs⊕uτ+1-Δs))
(6)
fl=FC(GRU(Xτ+1-qΔl⊕uτ+1-qΔl
Xτ+1-(q-1)Δl⊕uτ+1-(q-1)Δl,…,Xτ+1-Δl⊕uτ+1-Δl))
(7)
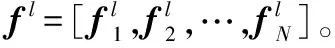
3.4 情境感知注意模块
前面的模块已经预测出了三个结果,即fi、fs、fl。在本节中,利用注意力机制,通过考虑情景信息来整合这三种预测结果,这是第一次尝试。
在时刻tτ+1处为每个区域rn构造了情景特征向量,用gn表示。在这里,考虑了三个主要的环境因素,包括tτ+1时刻的天气情况、tτ+1时刻的索引、rn区域的功能,这三个环境因素对出租车需求产生不同影响。外部因素的特征提取中专门采用了同样的方法,将时间索引嵌入到一个低维向量中,并与天气状况向量和区域函数向量相连接。
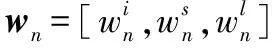
(8)
注意,权重表明预测结果的程度大小。
由于出租车需求预测是一个回归问题,采用均方误差作为损失函数,并通过将预测结果与真实情况的误差最小化来训练网络模型,即:
(9)
式中:Ω是网络模型中所有可学习参数的集合。
4 实验与结果分析
4.1 比较方法
将本文模型与以下方法进行比较。
(1) 历史平均值(HA):通过同一时段的平均历史出租车需求,预测每个地区下一个时段的出租车需求。
(2) 自回归综合移动平均值(ARIMA)[5]:是一种广泛应用于时间序列预测问题的方法,它通过结合移动平均值和自回归分量对时间相关性进行建模。
(3) 长短期记忆(LSTM)[7]:是循环神经网络的一种变体,可以从序列数据中有效地学习长期和短期的潜在相关性。
(4) 扩散卷积循环神经网络(DCRNN)[14]:将图形卷积集成到门控循环单元中,以预测道路网络上的交通流量。在该模型中,采用双向图随机游走操作,提取交通流量的空间动态,并用RNN捕捉时间动态。
(5) 时空图卷积网络(STGCN)[15]:由几个时空模块组成,这些模块用完全卷积层构建,用于处理车流量预测任务。具体地说,每个块由图像卷积和门控时间卷积组成,共同处理图结构的时间序列。
注意,为了通过DCRNN和STGCN预测出租车需求,为这两种方法构造了一个图,其中每个节点代表一个区域,每条边代表两个区域中心之间的距离。
并对模型中不同模块的性能进行分析,研究其在出租汽车需求预测中的有效性。
• 实时时空模块(ISTM):只使用实时时空模块,此模块包括LC层和GRU。
• 短/长周期模块和情境感知注意模块(PM+CAAM):只使用两个周期性模块,同时考虑短周期和长周期。两个模块的输出由情景感知注意模块进行整合。
• 无LC的实时模块、短/长周期模块和情景感知注意模块(IM+PM+CAAM):分别使用无LC层的实时时空模块和周期性模块预测出租车需求。三个模块的输出由情景感知注意模块进行整合。
• 实时时空模块和短/长周期模块(ISTM+PM):只使用实时时空模块和周期模块,它们的输出由网络训练过程中学习的权值张量进行整合。
• 基于注意力机制的卷积循环网络(ACRN):只考虑实时时空模块中相邻区域之间的空间相关性,忽略了功能相似区域。网络的其他部分与CACRNN相同。
4.2 实验设置
实验中参数的默认值设置如下。将时间间隔设置为15分钟,在实时时空模块中,使用了6个连续的时间片段,即o=6。此外,将参数默认设置为k=16、M=15、L=3和K=5。在短/长期周期模块中,分别采用4个和2个周期时间片段,时间间隔Δs=96(一天)、Δl=96×7(一周)。将天气状况、假期状况和周末分别用1×3向量表示。三个模块中GRU中的隐藏节点数均设置为512个。在情景感知注意模块中,将时间索引用1×5向量表示。
使用纽约市2016年6月的历史记录作为测试数据,其余记录作为训练数据。此外,采用中国大型城市成都的实际数据集进行了实验,以进一步验证本文方法与上文提及的基准相比的性能。成都所使用的数据集如下。
道路网络数据集成都市道路网络由756条道路组成。在此实验中,采用了成都市部分区域(由以下坐标包围: [北纬30.727 818°,东经104.043 333°],[北纬30.726 490°,东经104.129 076°],[北纬30.655 191°,东经104.129 591°],[北纬30.652 828°,东经104.042 102°]),按路段划分为623个区域。
出租车行程数据集滴滴网发布了成都市2016年11月1日至2016年11月30日出租车出行记录数据集,共4 141 504次。
POI数据集使用了成都地区146 587个POI数据,将其分为13个不同的类别。
气象和节假日数据集还使用了2016年11月1日至2016年11月30日的气象记录数据,包含22个工作日和8个周末。
通过均方根误差(RMSE)和平均绝对误差(MAE)评价每种方法的性能。此外,对于所有基于DNN的模型,均采用Adam优化算法来训练参数。Adam的学习率设置为10-4,训练的批量大小为64。还将训练提前停止,其中回合数和训练次数分别设置为6和100。所有的实验都是在NVIDIA RTX20700显卡上进行的,实验结果是在相同参数下使用不同的随机种子进行5次运行计算,然后取这5次计算结果的平均值。
4.3 实验结果
4.3.1各模型在基准下的比较
表2和表3分别显示了本文模型和默认参数设置下的基准所实现的性能。很容易发现,与所有基准相比,本文模型在不同的数据集下达到了最低的RMSE和MAE。具体来说,HA和ARIMA表现最差。结果表明,深层神经网络(如LSTM)可以有效地应用于城市数据预测。此外,由于LSTM只对出租车需求的时间相关性进行建模,因此LSTM的性能比本文模型差。在基准中,STGCN和DCRNN都获得了良好的性能,它们同时捕获了空间和时间的相关性。与DCRNN相比,模型在纽约市数据集上的RMSE(MAE)降低了9.4%(13.6%),在成都市数据集上的RMSE(MAE)降低了13.0%(8.5%)。与STGCN相比,模型在纽约市数据集上的RMSE(MAE)降低了8.9%(12.9%),在成都市数据集上的RMSE(MAE)降低了14.4%(23.6%)。

表2 性能比较——纽约市
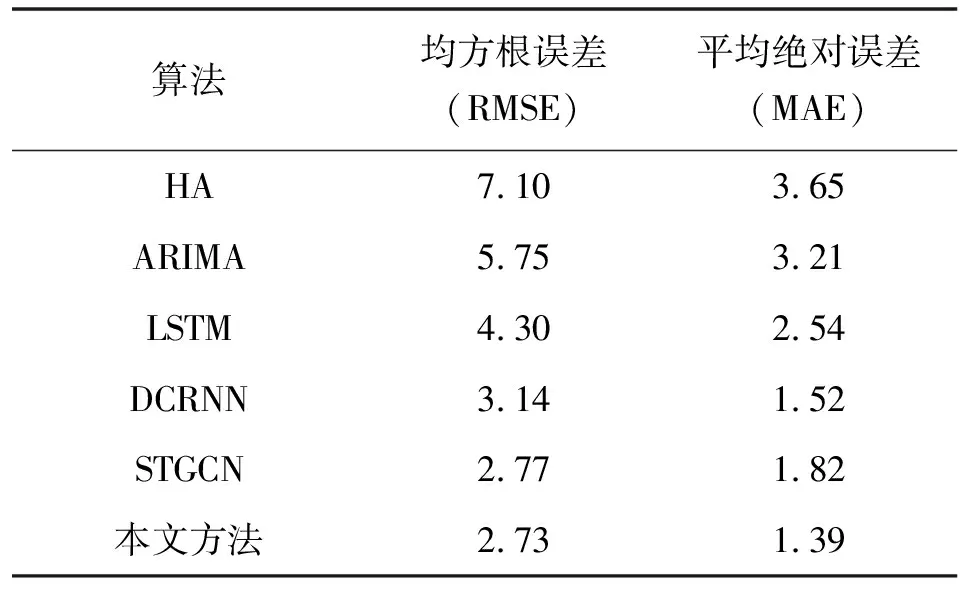
表3 性能比较——成都市
4.3.2模块评估
评估本文模型中不同模块的有效性,结果分别如表4和表5所示。很容易发现,在本文模型中,每一个模块都有更好的预测性能。特别地,通过比较ISTM和ISTM+PM的结果,确认了周期性模块的工作有效性。由于PM+CAAC的性能比本文模型差,可以得知实时时空模块是起到一定作用的。通过IM+PM+CAAM与本文模型的比较,验证了LC层提取不同地区出租车需求空间相关性的有效性。很明显,本文模型取得了比ISTM+PM更好的性能,这证实了情景感知注意模块的有用性。此外,CACRNN考虑了功能相似区域的空间相关性,提高了ACRN的性能。
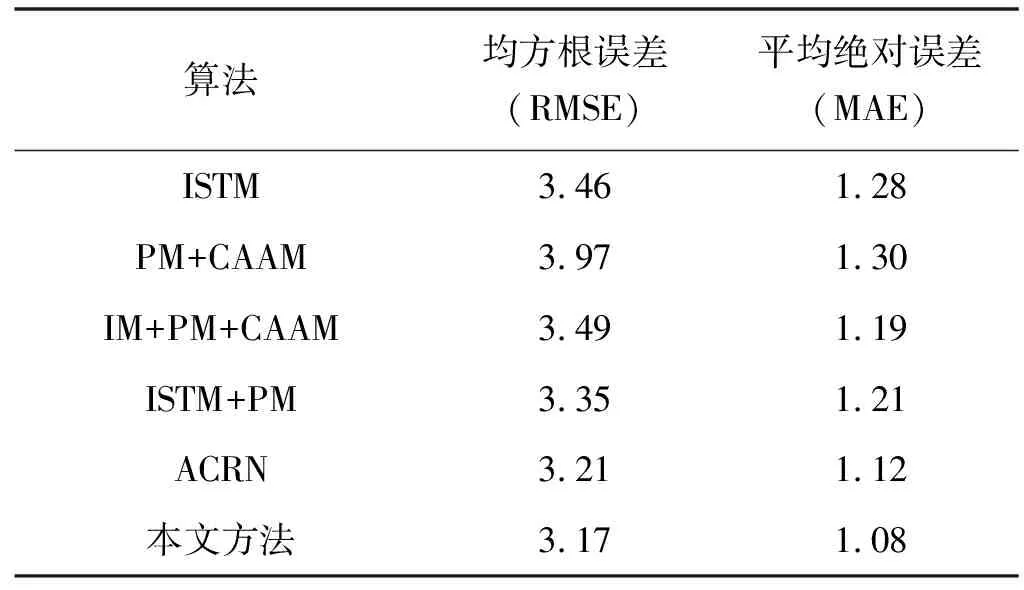
表4 模块评估——纽约市
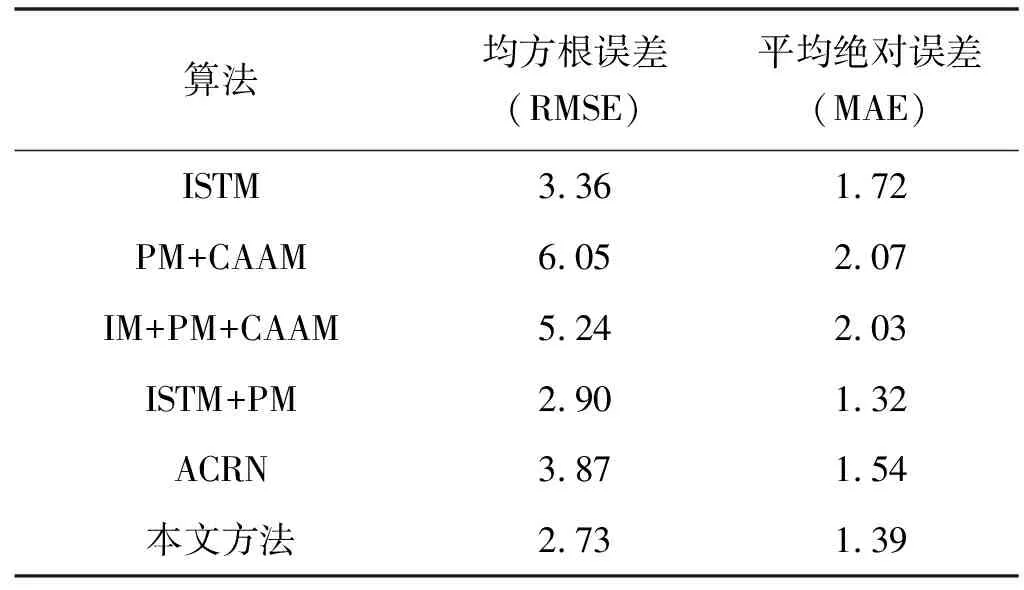
表5 模块评估——成都市
4.3.3时间效率评估
分别评估了本文模型和较先进的基于DNN(即STGCN和DCRNN)所获得的时间效率,以及训练和测试过程的时间消耗。如表6所示,尽管DCRNN的可训练参数数量最少,但其训练和测试所花费的时间远远大于STGCN和CACRNN。此外,与STGCN相比,本文提出的CACRNN在训练和测试过程中的时间消耗更高。这是因为CACRNN的可训练参数几乎是STGCN的18倍。众所周知,在训练过程中计算反向传播过程中的参数梯度是非常耗时的。在实际应用中,由于DNN模型可以预先训练,所以需要更注重测试的时间效率。幸运的是,可以观察到CACRNN在测试过程中只比STGCN多花费17 ms,这是可以接受的。
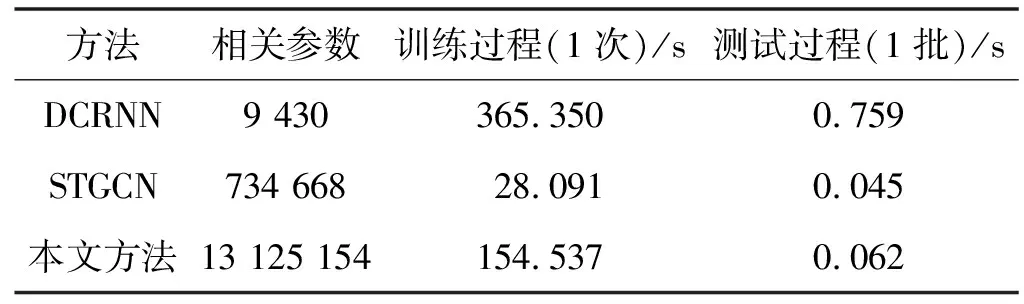
表6 时间消耗
4.3.4参数的影响
还评估了CACRNN不同模块中一些关键参数的影响,即L个LC层数、实时模块o中的时间片段数、短周期模块p中的时间片段数、长周期模块q中的时间片段数。即保持其他参数不变,改变研究对象参数,通过改变参数大小观察参数对预测精度指标的影响。在图9中,可以发现当L从0到3变化时,MAE和RMSE减小,从而验证了相邻区域之间的深层空间相关性的提取。另一方面,当L从3变为5时,RMSE和MAE略有增加,因为随着L的增加,更多不相关的区域会进行卷积运算,并对预测结果产生负面影响。 如图10-图12所示,当o从0变为8、p设为8、q设为4时,MAE和RMSE先减小然后增大。这表明在特定的时间段(例如90分钟)内,出租车需求之间存在时空相关性,这有助于细粒度出租车需求的预测。此外,出租车需求具有一定的日周期性和周周期性,其过去4天和两周的出租车需求包含了最有用的信息。

图9 LC层数的影响

图10 o长度的影响
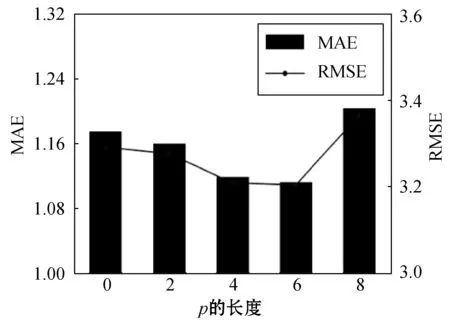
图11 p长度的影响
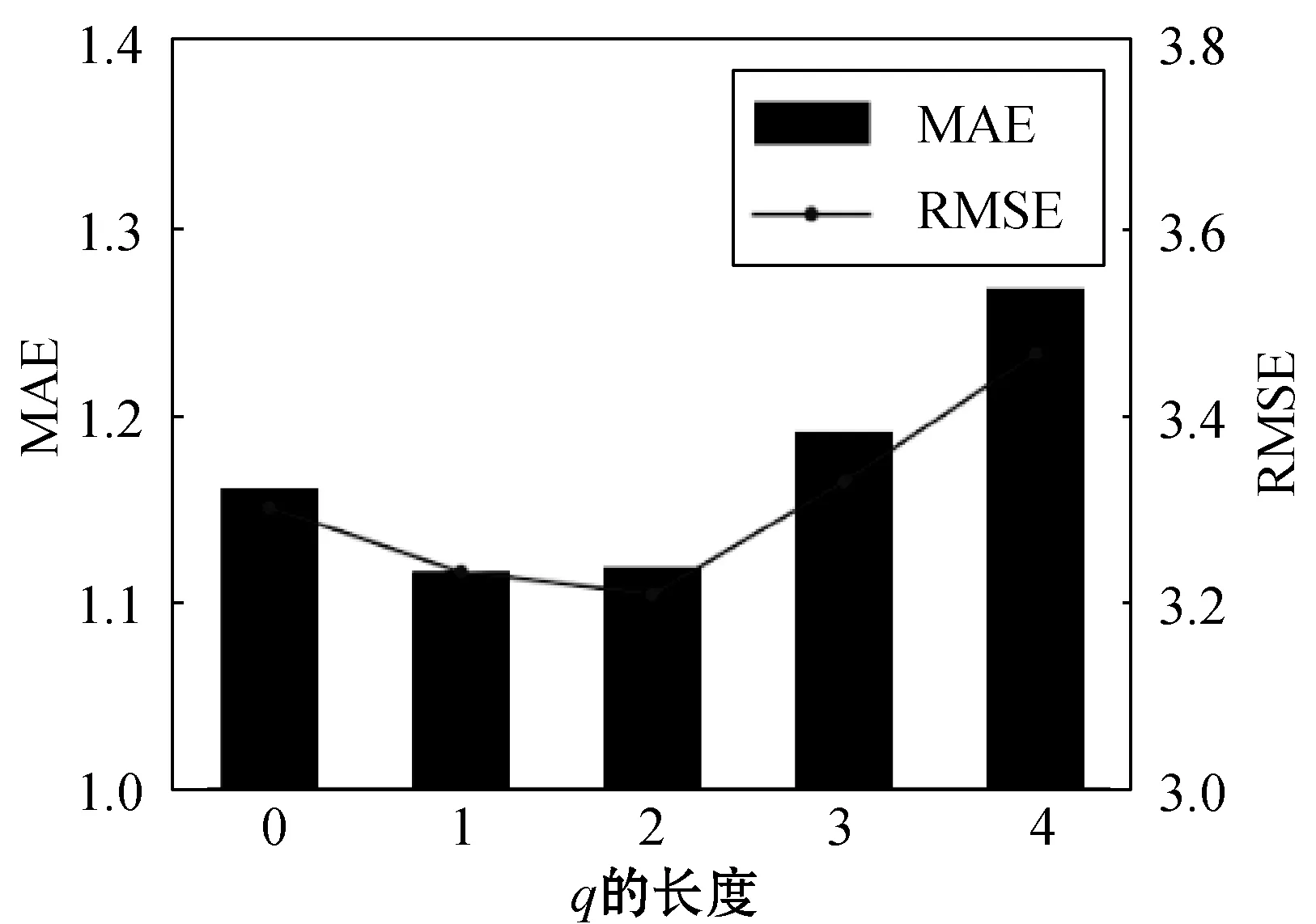
图12 q长度的影响
4.3.5时空相关因素的影响
进一步评估天气、节假日、局部区域等因素对预测精度的影响,分别将考虑天气、节假日、局部区域的数据与不考虑上述因素的数据作为训练数据,最后通过测试数据进行预测,相应的对比结果如表7所示。
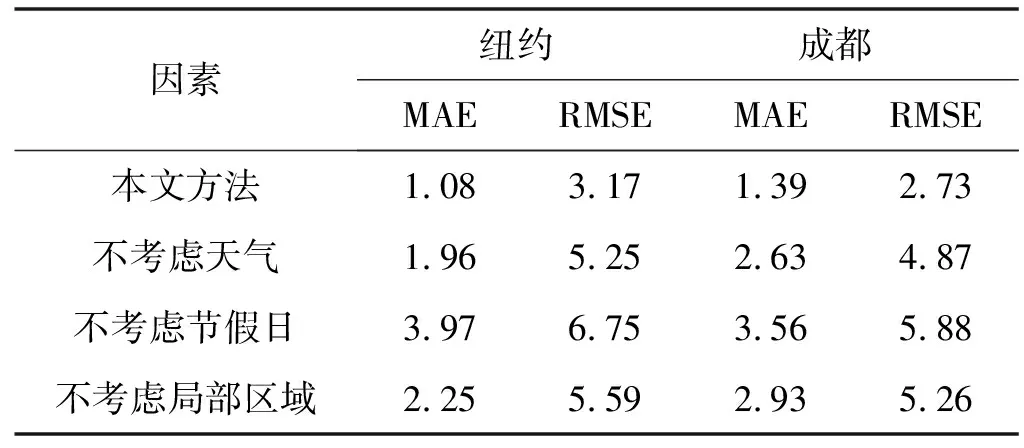
表7 时空相关因素对预测结果的影响
可以看出,考虑了天气、节假日与局部区域因素的预测精度明显高于不考虑这些因素的预测精度。这进一步证明了充分考虑各个因素对预测精度的提升有较大的作用,也更符合实际情况。
5 结 语
针对出租车需求预测方法中由于数据挖掘深度不够导致的预测精度较低问题,提出一种基于情境感知注意机制的循环卷积神经网络出租车需求预测方法。通过纽约市和成都市的实际数据集综合实验结果可得如下结论:
(1) 情景感知注意模块、功能相似区域、时空相关性等因素的引入,有利于出租车需求预测精度以及预测速度的提高。
(2) 引入短期/长期周期性模块,使得方法对于长期短期出租车需求预测均具备较好的预测性能。
(3) 与现有的方法相比,本文方法在预测精度以及预测速度上具有较大的优势,进一步证明了本文算法的有效性。
