基于深度学习的公路运价预测模型研究

王敏

摘 要：随着现代物流行业的发展，公路运输作为一种重要的货物运输方式正在扮演着越来越重要的角色。公路运输具有灵活、快速、点对点等优势，尤其对于短途、小批量货物运输需求更加广泛。公路运价预测作为运输流程的关键环节之一，已成为政府部门和物流业关注的焦点问题。公路运价预测任务受到多种因素影响，如市场需求、运输距离、油价和政策变化等。这些因素之间相互作用，增加了公路运价准确预测的难度。针对这个问题，文章提出了一种基于深度神经网络的公路运价预测模型，以应对公路运价预测的挑战。其主要贡献在于：传统的多变量时序预测模型采用线性或非线性回归模型，但这些模型往往受到变量之间非线性、时间动态性和复杂依赖性的建模能力限制。文章采用基于图神经网络的MTGNN模型，对公路运价预测进行了应用研究。该模型由图卷积网络和时序卷积网络两部分组成。首先，通过神经网络学习图结构并计算邻接矩阵来表示节点之间的依赖关系和实现节点聚合。然后，使用图卷积网络模块对节点信息進行传播，从而获取更准确的节点表示。接下来，时序卷积网络提取经过图卷积网络学习后结果中的时序特征，实现对未来公路运价的预测。最后，输出层对时序输出结果进行计算，得出模型预测结果。

关键词：公路运价；多变量时序预测；图神经网络

中图分类号：F542；U4 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2023.12.006

Abstract： With the development of modern logistics industry， road transportation is playing an increasingly important role as an important mode of freight transportation. Road transportation has advantages such as flexibility， speed， and point-to-point service， especially for short-distance and small-batch cargo transportation. However， predicting road freight rates， as one of the key links in the transportation process， has become a focus of attention for the logistics industry and government departments. The prediction of road freight rates is influenced by various factors， such as market demand， transportation distance， oil prices， and policy changes. The interaction between these factors makes it difficult to accurately predict road freight rates. To address this issue， this paper proposes a road freight rate prediction model based on deep neutral network to meet the challenges of predicting road freight rates. The main contribution of this paper is： In traditional multivariate time series prediction models， linear or nonlinear regression models are often used. However， these models are often limited in their ability to model non linearity， time dynamics， and complex dependencies between variables. In this study， the MTGNN model based on graph neural networks was applied to highway freight rate prediction. The model consists of two parts： graph convolutional network （GCN） and temporal convolutional network （TCN）. First， the neural network learns the graph structure and calculates the adjacency matrix to represent the dependency between nodes and achieve node aggregation. Then， the GCN module is used to propagate node information and obtain more accurate node representations. Next， the TCN extracts temporal features from the results learned by the GCN to predict future highway freight rates. Finally， the output layer calculates the time series output results to obtain the model's prediction.

Key words： road freight rate; multivariate time series forecasting; graph neural network

0    绪    论

公路物流货运价格是物流行业中的一个重要方面。近年来，研究人员对其进行了大量的定性研究。例如顾敬岩等[1]通过对我国公路物流货运价格波动特征的定性分析发现，价格波动主要由市场供需关系、政策调控、竞争状况和成本等因素导致。他们进一步深入探讨了公路货运市场价格调节机制失灵的根本原因，发现市场信息不对称、价格管制不力、垄断行为等因素也对价格波动产生了重要影响。针对这些问题，他们从市场和从业者的角度提出了多项建议措施。研究人员在公路物流货运价格方面的分析与探讨是非常丰富的。例如马银波[2]对公路货运价格与公路货运量之间的关系进行了分析，并从经济学的角度解析了短期供给特征和行业运行状况。他还探讨了运价的走势规律以及运价问题的成因。通过这些分析，深入挖掘了公路货运价格背后的内在规律。另外，戴宏[3]对我国公路货运物流服务价格存在的主要问题进行了系统性探讨，并提出了一系列针对性建议。例如在融资渠道方面，建议加强资本市场的建设，拓展企业融资渠道。在模式创新方面，提倡发展多式联运、物流园区等新型物流模式。在供给侧改革方面，建议完善市场机制，加强监管，提高行业自律能力等。

在时间序列预测任务上，已经有了很多性能较好的研究。Sean J. Taylor和Benjamin Letham提出Prophet模型，通过将时间序列分解成季节项、趋势项、剩余项和节假日效应四个部分，并对每个部分进行分析拟合，最后累加起来得到最终的预测值。无独有偶，Büyük?ahin ? ?等人提出将时间序列数据分为线性项（L）和非线性项（N），再拟合。还有研究通过分解模型而不是分解数据的方式进行，例如经验模态分解（EMD）变分模态分解（VMD）、小波分解（WD）等。对分离后的信号再用数学模型进行拟合、叠加、重构，就能得到最后的预测值。还有的通过NLP经典模型Seq2Seq去学习时间序列，通过残差连接改进卷积网络WaveNet和时序神经网络LSTNet。

但是，基于神经网络的公路运价预测研究还有很多问题有待解决。第一，数据获取困难。公路运价涉及多个因素，如货物类型、货物重量、运输距离、车型、路况和市场需求等，需要大量的数据进行建模。但是，公路运价的数据不容易获取，需要考虑数据的保密性、获取渠道的限制等问题。第二，建模复杂度高。首先，公路运价预测需要考虑多个因素的影响，如供需关系、成本变化、市场竞争等。同时，这些因素之间的关系非常复杂，需要采用多种数据分析和建模方法才能建立准确的预测模型。其次，市场环境不稳定也是一个重要原因。铁路运价受市场环境的影响，如政策法规、自然灾害等，这些因素可能对铁路运价的预测造成一定干扰。此外，公路运输市场的变化也非常迅速，需要不断更新预测模型来适应市场需求。最后，模型可解释性差也是缺点之一。某些公路运价预测模型，如神经网络和支持向量机等，具有较高的预测准确性，但是由于其内部机制复杂，导致模型的可解释性较差，难以对预测结果进行解释和说明。

1    公路运价预测应用研究

本文采用了基于图神经网络的公路运价预测模型，其首先利用神经网络对图结构进行学习，同时计算图的邻接矩阵，然后利用图卷积网络模块对节点信息进行传播，最后利用时序卷积网络对经过图卷积网络学习后的结果进行时序特征提取，并将时序输出的结果通过输出层进行计算，最终获得模型预测结果。

1.1    问题提出

接下来，针对基于图神经网络的多变量时序预测任务给出正式描述：假设有一个时间序列S={x1，x2，...，xT}，其中xt∈RD表示在时刻t的D维向量。对于一个给定的长度为N步的多变量时间序列X={xt1，...，xtN}，基于图神经网络的多变量时间预测方法就是利用图神经网络对S进行学习得到一个预测函数f，其能够对输入序列X预测其未来第M步之后的变量值Y={xtN+M}或者之后M步内的变量变化情况Y={xtN+1，...，xtN+M}进行预测。

1.2    基于图神经网络的时序预测模型

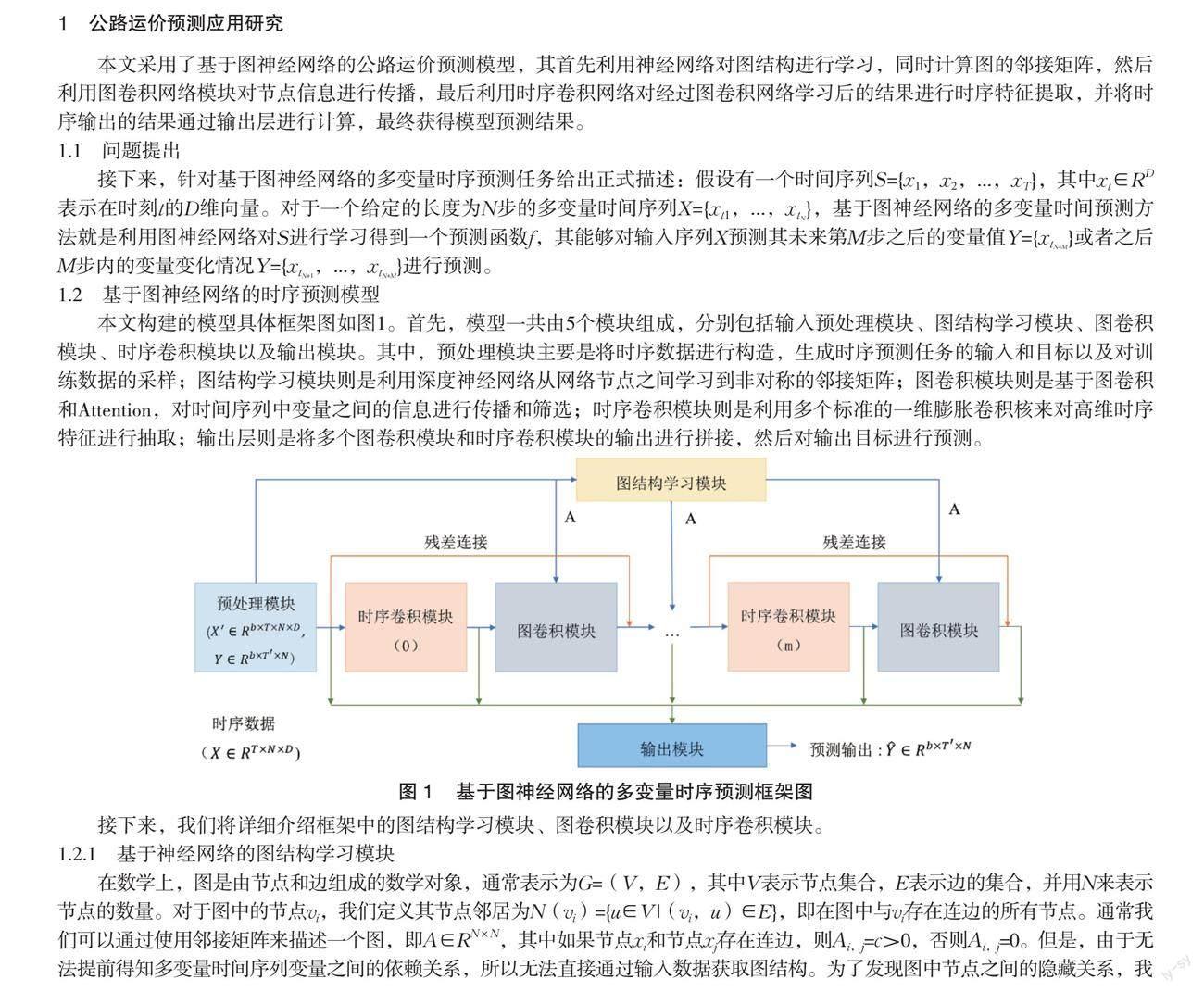
本文构建的模型具体框架图如图1。首先，模型一共由5个模块组成，分别包括输入预处理模块、图结构学习模块、图卷积模块、时序卷积模块以及输出模块。其中，预处理模块主要是将时序数据进行构造，生成时序预测任务的输入和目标以及对训练数据的采样；图结构学习模块则是利用深度神经网络从网络节点之间学习到非对称的邻接矩阵；图卷积模块则是基于图卷积和Attention，对时间序列中变量之間的信息进行传播和筛选；时序卷积模块则是利用多个标准的一维膨胀卷积核来对高维时序特征进行抽取；输出层则是将多个图卷积模块和时序卷积模块的输出进行拼接，然后对输出目标进行预测。

接下来，我们将详细介绍框架中的图结构学习模块、图卷积模块以及时序卷积模块。

1.2.1    基于神经网络的图结构学习模块

在数学上，图是由节点和边组成的数学对象，通常表示为G=（V，E），其中V表示节点集合，E表示边的集合，并用N来表示节点的数量。对于图中的节点vi，我们定义其节点邻居为N（vi）={u∈V|（vi，u）∈E}，即在图中与vi存在连边的所有节点。通常我们可以通过使用邻接矩阵来描述一个图，即A∈RN×N，其中如果节点xi和节点xj存在连边，则Ai，j=c＞0，否则Ai，j=0。但是，由于无法提前得知多变量时间序列变量之间的依赖关系，所以无法直接通过输入数据获取图结构。为了发现图中节点之间的隐藏关系，我们采用一个基于神经网络的图结构学习模块来计算图的邻接矩阵，进而从时序数据中自适应地捕获变量之间的空间关系。

目前，用于计算节点之间相似性的方法通常是对称的或者双向的，但是对于公路运价的多变量时序数据来说，变量之间的关系应该是单向的，即前一个时间的节点状态变化会引起后面其他节点的变化，但是反过来无法影响，所以我们在学习图结构的时候，应该主动引入邻接矩阵具有非对称的属性约束。具体网络设计如下。

其中，E1和E2分别表示从原始节点中随机采样的两个节点学习后得到的表征，θ1，θ2表示模型参数，α表示激活函数的饱和率，argtopk（·）用于返回在给定向量中前k个最大值的索引位置，这是在计算邻接矩阵时常用的一个操作。在处理图神经网络时，M1和M2表示节点在网络中的输出结果，它们包含了节点之间的空间关系信息。为了更好地表示空间依赖关系，我们可以通过计算M1乘以M2的转置（M1MT2）来对这些关系进行重新建模，然后通过公式（3）来计算邻接矩阵的非对称信息。其中，ReLU激活函数可以起到正则化邻接矩阵的效果，当Ai，j＞0时，有邻接矩阵的对角元素Aj，i＜0，通过激活函数后会使其值变为0。ReLu函数可以确保邻接矩阵中的元素非负，同时还能在一定程度上强化邻接矩阵的稀疏性。这样的正则化效果有助于提高模型的泛化能力，减少过拟合的风险。最后，为了降低后续图卷积网络的计算代价，利用公式（4）对图进行稀疏化，即只包括与节点最近的k个节点的邻接矩阵值，其余值均赋值为0。

1.2.2    图卷积模块

模型中的图卷积模块主要是利用通过学习得到的邻接矩阵和通过时序卷积后得到的节点特征矩阵来对数据的空间依赖性特征进行学习。这里对信息的处理包括两个子模块：信息传播和信息选择。并且使用MixHop作为图卷积网络模型。

MixHop是一种改进的图卷积网络模型，它使用多个邻接矩阵进行卷积操作，能够捕捉更多节点之间的关系。在MixHop模型中，每个卷积层使用多个邻接矩阵来更新节点特征向量，这些邻接矩阵可以有不同的权重和阶数。其核心思想是将多个不同邻接矩阵的信息进行融合，从而提高模型的表达能力。MixHop模型的卷积操作如下。

其中，Hl表示第l层节点的特征矩阵，Ai表示第i个邻接矩阵，Wi（l）表示第i个邻接矩阵对应的权重矩阵，k表示使用的邻接矩阵的数量，σ表示激活函数。

1.2.3    时序卷积模块

时序卷积模块参考了LSTM的门控设计，采用了两个膨胀卷积Inception模块。这两个模块分别充当滤波器和信息控制器。第一个膨胀卷积Inception模块在输出后使用tanh作为激活函数。tanh函数能将输出值映射到-1～1之间，起到滤波器的作用。这个模块主要负责提取时序特征并生成对应的表征。第二个膨胀卷积Inception模块使用sigmoid作为激活函数。sigmoid函数将输出值映射到0～1之间，这样就能控制信息量的传递。这个模块的作用是根据输入数据的特征来决定哪些信息可以通过过滤器传递给下一个模块。

1.2.4    输出模块

由表1我们可以观察到，最终输入模型输出层的信息为多个模块的拼接。其中，输出层包含两个1×1的卷积层，对于单步预测，输出层最终输出长度为1的预测结果。

由于网络模型设计中涉及深层的神经网络，其存在大量的非线性激活函数和权重参数，信号经过多次传递可能会出现梯度消失或梯度爆炸的情况，从而导致网络无法进行有效的学习。所以，为了更快地训练模型，在模型网络结构中也引入了残差连接。残差连接通过直接将输入特征添加到网络中间层的输出特征上，从而使网络信号能够绕过一部分非线性变换和权重参数，保证梯度能够在网络中进行有效传播，从而提高网络的学习能力和效率。

1.3    实验设置

1.3.1    数据描述

本文涉及的数据来源包括中华人民共和国国家统计局官网和大型运输公司，涵盖了2016年1月—2022年7月的公路货运量与公路运价数据。为了更准确地掌握公路运价的变化趋势和规律，本文采用了按周采集数据的方法进行实证分析，以更好地捕捉公路运价的变化趋势。这些数据的采集和处理过程，将有助于公路运价预测，并能为相关的政策制定提供有力的依据和支持。

数据集划分采用留出法，是指将数据集按照一定的比例划分为训练集和测试集。训练集用于构建预测模型，测试集用于评估预测模型的性能。本文中将2016年7月—2021年9月作为训练数据，2021年9月—2022年9月作为测试数据。

1.3.2    评价指标

本节选择5个不同的指标来对算法结果进行测试，分别为平均绝对误差、均方误差、均方根误差、平均絕对百分比误差和R2。R2（R-squared，Coefficient of determination）是一种用于评估回归模型拟合程度的统计量。它的取值范围从0到1，越接近1表示模型对数据的拟合程度越好。由表1可以看出，MTGNN模型在相关性指标R2上取得了最好的成绩。

1.4    实验与评估

1.4.1    基线算法

TCN（Temporal Convolutional Network）是一种基于卷积神经网络的时序预测模型，能够自适应地捕捉时序数据中的长期依赖关系。相比于传统的循环神经网络，TCN模型具有更短的训练时间、更少的参数和更好的预测性能。

DeepAR模型是基于循环神经网络（RNN）和卷积神经网络（CNN）的混合模型，其核心思想是将目标序列与其他相关时间序列联合训练，从而提高模型的预测准确性。在模型训练过程中，DeepAR模型不仅考虑了目标序列的历史信息，还结合了其他相关序列的历史信息，从而更好地捕捉序列中的趋势和季节性等时间特征。

N-BEATS（Neural basis expansion analysis for interpretable time series forecasting）是一种基于神经网络的时间序列预测模型。N-BEATS模型采用可分解的堆叠基函数来建模时间序列数据，并利用多层神经网络对其进行扩展和组合，从而实现高精度的预测。N-BEATS模型更加灵活和高效，具有更好的可解释性和预测性能。

NHits模型是一种用于时间序列预测的深度神经网络模型，它是N-BEATS模型的改进版。NHits模型使用类似于N-BEATS模型的框架，但引入了一种称为Multi-Horizon Transformer的新型深度神经网络结构，该结构具有更好的特征提取能力和跨时序预测能力。

1.4.2    实验结果与分析

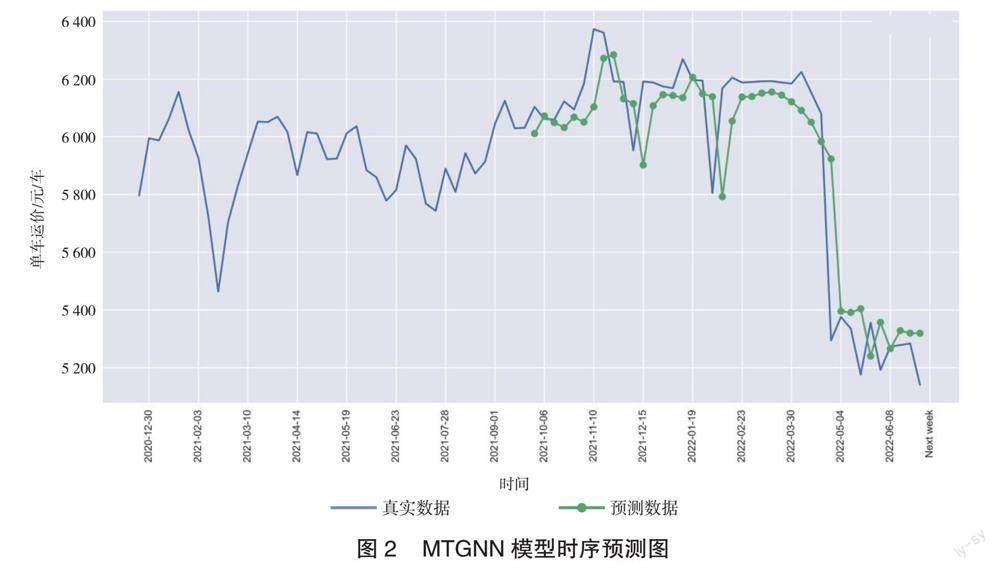
本文中应用的基于图神经网络的时序预测模型MTGNN，在公路运价预测任务上取得了最为优异的表现。如图2所示，其直观地展示了MTGNN模型处理时序数据时强大的能力和有效性。MTGNN可以同时处理多个时序数据，包括节点属性、边属性和时间属性等，可以在不同层级上学习数据的表示，并将多个维度的信息相结合，以提高模型的表达能力。在公路运价预测任务中，公路运价会受到季节变化、时间趋势和短期事件等多种因素的影响，MTGNN模型可以同时对这些因素进行建模，从而提高预测的准确性。MTGNN模型采用了图神经网络来建模节点之间的依赖关系，通过學习节点之间的依赖关系，能够更好地捕捉节点之间的复杂关系和依赖性，从而提高预测的准确性。在公路运价预测任务中，各个路段之间的运价存在复杂的依赖关系，MTGNN模型能够学习这些依赖关系，并利用这些信息来提高预测的准确性。MTGNN可以自适应地学习图结构，包括节点之间的连接和边的权重，可以在不同时间步骤上学习不同的图结构，并对图结构进行自适应更新，从而以提高模型的预测能力和鲁棒性。

2    结    语

基于图神经网络的公路运价预测模型主要包括两个部分：图卷积网络和时序卷积网络。首先，模型利用神经网络对图结构进行学习，计算图的邻接矩阵，并通过邻接矩阵来表示节点之间的依赖关系，从而实现节点之间的聚合。然后，利用图卷积网络模块对节点信息进行传播，将节点特征传递给它们的邻居节点，从而得到更准确的节点表示。接下来，时序卷积网络对经过图卷积网络学习后的结果进行时序特征提取，从而提取出有用的时序信息，以实现对未来公路运价的预测。最后，利用输出层对时序输出的结果进行计算，最终获得模型预测结果。基于图神经网络的公路运价预测模型能够有效地利用节点之间的依赖关系，提高预测的准确性和可解释性，特别是在公路运价具有空间依赖关系和时间依赖关系的情况下。因此，该模型在实际应用中具有广泛的应用前景，可为交通运输决策提供有价值的参考。

参考文献：

[1] 顾敬岩，吴群琪．我国公路货运市场价格的演进趋势、问题及对策[J]．交通运输系统工程与信息，2013，13（6）：191-197.

[2] 马银波．我国公路货运价格特性分析[J]．综合运输，2007（9）：69-72.

[3] 戴宏．我国公路货运物流服务定价机制研究[J]．价格理论与实践，2016（12）：74-76.