某型双机身飞机水上迫降数值模拟
2023-08-08孙肖元邓枫刘学强
孙肖元, 邓枫, 刘学强
(南京航空航天大学 航空学院 飞行器先进设计技术国防重点学科实验室, 江苏 南京 210016)
0 引言
随着跨水域飞行航线日益增加,飞机在飞行过程中遇到紧急情况需要水上迫降的可能性随之提高。因此,关于飞机水上迫降和入水冲击等跨介质过程的研究需要加以重视。通常,针对入水砰击问题的研究方法主要分为理论研究、试验研究和数值模拟研究。
在理论研究方面,关于入水冲击的研究最早可以追溯到1929年,von Karman[1]做了水上飞机降落时的入水砰击载荷研究。其利用动量守恒定律将飞机入水砰击过程理想化,成为一个二维楔形体的入水砰击过程,由此提出了关于物体入水砰击的流体理论,得出了最早的关于砰击载荷研究的理论。Wagner[2]引入了势流理论的原理,并由此提出了将楔形体等效成一个扩展的平板结构,通过求解流体的速度势方程,再利用伯努利方程得出砰击载荷在平板表面的分布情况。Verhagen[3]利用板边缘处的射流效应对压力的分布进行了一定程度的光顺处理,从而能够计算出板边缘处的压力分布情况。Peseux等[4]采用三维Wagner理论和有限元方法,分析了圆锥体砰击问题。Greenhow[5]讨论了刚性物体的喷溅根部压强问题。Zhao等[6]给出了一般形状物体入水砰击的计算方法。闫发锁等[7]以Wagner的入水砰击理论为基础,提出了楔形体砰击压力的计算方法,并且通过相关实验的对比验证,得出了完整的压力计算方法。
在实验研究方面,Bocquet[8]利用圆形铝板做了打水漂实验,分别研究了速度、姿态角和入水角对水漂实验的影响。Takagi等[9]做了关于砰击载荷影响的实验研究,通过改变模型的底板倾斜角和厚度,来测量结构的应力和加速度等数值的变化。孙辉等[10]做了关于V型板入水的响应实验,得到了结构体入水的加速度以及应力响应等实验数据。刘晖[11]设计了不同刚度楔形体的入水砰击实验,主要研究刚度这一参数对入水砰击时的影响。Mcbride等[12]进行了9种不同机身形状等比例缩小模型的迫降实验,测量了模型的水平速度、姿态角、质心高度的变化。Yettou等[13]研究了对称三维楔形体的入水砰击过程,其实验结果可为入水砰击数值模拟研究提供实验数据。蒲锦华等[14]通过TEMA图像运动分析软件跟踪判读高速摄像结果,获得了某型飞机模型迫降着水瞬间的运动状态。骆寒冰等[15]采用落体入水模型研究了砰击过程的砰击压力与结构动响应规律。
在数值模拟研究方面,陈震等[16]利用MSC-Dytran仿真软件对二维楔形体入水问题进行了数值模拟研究,阐述了空气垫和重力对砰击时液面的变化和根部的喷射具有一定的影响。张晓波[17]应用大型有限元软件LS-DYNA模拟了二维刚性体的入水砰击过程,研究了刚性体的入水高度、壳的厚度、有无沙漏现象、罚函数的系数选择和重力等因素对入水过程的影响。王建凯[18]采用ANSYS-Fluent流体分析软件模拟了物体的入水砰击过程,研究了模型剖面的压力分布和监测点垂向作用力的数值变化,得出了相对运动最大的部位最易发生砰击现象、砰击压力峰值与船体剖面形状具有一定的关系的结论。陈光茂等[19]利用光滑粒子流体动力学(SPH)方法对二维楔形体进行了仿真数值模拟,并将竖直方向的速度变化与实验数据进行了对比验证。骆寒冰等[20]利用LS-DYNA软件研究三维楔形体的入水砰击问题,采用基于任意拉格朗日-欧拉(ALE)算法和罚函数的耦合算法对楔形体的入水砰击过程进行了数值模拟计算。卢昱锦等[21]综合利用流体体积(VOF)模型和整体动网格方法(GMM)对高速入水的三维平板数值模拟,并主要针对不同入水角度进行了数值模拟研究。陆召严[22]利用SPH方法对某型直升机缩比模型进行了俯仰角分别为6°、8°和10°的带有水平速度的水上迫降过程数值模拟。屈秋林等[23]结合VOF方法和GMM方法研究了NACA-TN2929模型各部件在水上迫降过程中的作用,计算结果表明飞机迫降过程中气动载荷的影响不可忽略。Yan等[24]利用SPH方法对三维圆盘水漂运动进行了数值模拟,其数值结果和理论分析结果为本文提供了算例验证数据。赵芸可等[25]采用6自由度(6DOF)模型和GMM方法成功模拟了某型飞机的迫降过程。李勐等[26]采用ALE方法对飞机非对称水上迫降过程进行数值模拟,分析了不同初始滚转角情况下飞机的运动响应与力学特性。田北晨等[27]采用VOF方法对跨介质飞行器触水滑跳过程展开数值模拟研究,主要研究了入水速度与入水俯仰角度对滑跳过程的影响。
随着计算机技术的发展,各式各样的数值模拟方法已经被应用于跨介质飞行器入水砰击问题的数值模拟研究。基于以上学者的研究,本文综合运用URANS方法、VOF方法、动网格技术和6DOF模型对某型双机身飞机的水上迫降过程进行数值模拟研究,重点研究飞机入水俯仰角度这一关键参数对该飞机水上迫降过程的影响机制,为飞机水上降落过程研究提供参考和技术支持。
1 数值计算方法
飞机水上迫降过程是一个复杂的物理过程,涉及固、液、气三者之间的相互作用。飞机水上迫降过程的数值模拟方法主要包括流体力学基本控制方程及求解、VOF方法、动网格技术和6DOF模型等。流体力学基本控制方程解决复杂的湍流和多介质流动问题,VOF方法实现对自由液面的追踪,动网格技术和6DOF模型模拟飞机水上迫降的运动过程。通过非定常计算的方式模拟飞机在水上迫降过程中的数值变化,通过控制变量法研究飞机俯仰角这一重要参数对飞机水上迫降过程数值的影响。本文采用计算流体力学(CFD)分析软件Fluent进行数值计算,其求解流程图如图1所示。
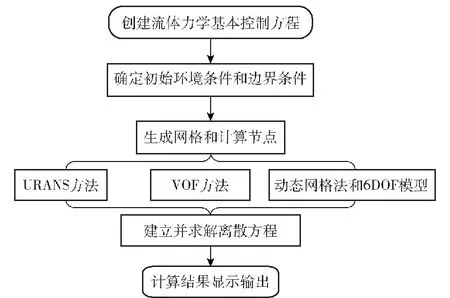
图1 数值模拟流程
1.1 流体力学控制方程
目前,CFD仿真计算都是基于流体力学基本控制方程,其控制方程包括3个基本方程:连续性方程、动量守恒方程和能量守恒方程。由于本文的数值计算不涉及传热问题,不考虑能量守恒方程。控制方程采用三维不可压缩URANS方程,其中包括连续方程和动量守恒方程。流体流动的连续方程可以表示为
(1)
式中:u、v、w分别表示某一空间点上x轴、y轴、z轴方向的流速。流体流动的动量守恒方程表示为
(2)
(3)
(4)
式中:p为流体中的压力;fx、fy、fz分别为x轴、y轴、z轴上的单位质量力;ρ为流体密度;μ为流体的动力黏度系数;μT表示标准k-ε两方程模型求解的湍流涡旋黏度。
1.2 VOF方法
VOF方法是一种能够及时捕捉并追踪自由界面的方法,具有操作简单、计算稳定和鲁棒性优异等优点。该方法中,互不相容的流体共同使用一套动量方程,并通过引入相体积分数这一变量来实现对流体计算域内自由界面的追踪。对于流场中的每个网格单元,相体积分数定义为目标流体的体积与网格单元体积的比值,通过计算每个网格上的相体积分数,实现对自由界面的追踪。通过对自由界面的追踪,可以将流场中的空气和水两种不同的介质清晰地展示出来,空气的VOF分数为0,水的VOF分数为1,而VOF分数介于0和1之间则代表水和空气两种介质的交界处,并通过求解VOF函数的控制方程实现交界面的呈现,其表达式为
(5)
式中:F为VOF函数。如图2所示,VOF方法通过求出整个计算域内每个网格单元的VOF分数,可以构建出水-空气相位交界面。为加快数值计算的收敛速度和增强计算稳定性,本文采用SIMPLEC算法处理流场内的压力-速度耦合。
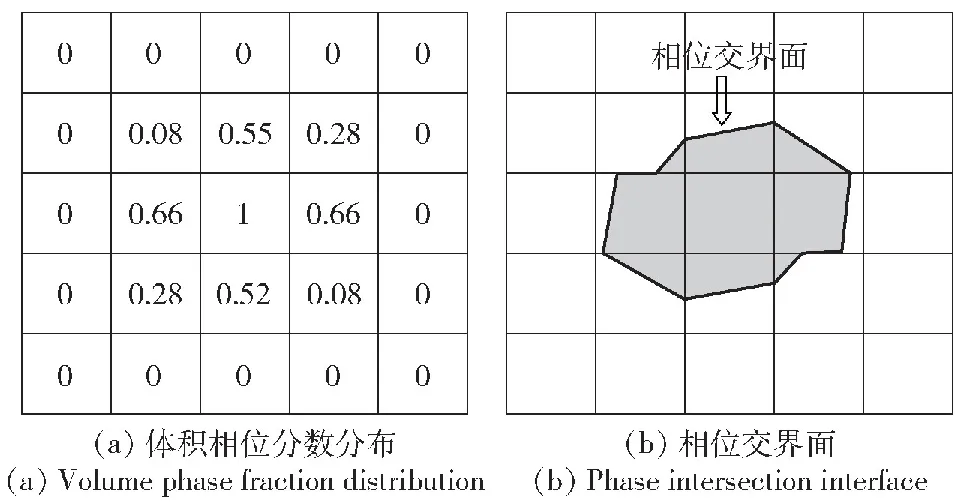
图2 相位交界面的呈现原理图
1.3 动网格技术与6自由度模型
综合运用动网格技术和6DOF模型实现飞机水上迫降过程的动态模拟。采用弹性光顺法和结构重构法等动网格方法。6DOF运动求解器能够解决基于平移和旋转自由度的物体运动过程,通过监视目标物体的6DOF数值变化进行数值模拟研究。如图3所示,一般物体在空间内具有6个DOF,即沿x、y、z3个直角坐标轴方向的平移自由度和绕x、y、z3个直角坐标轴方向的旋转自由度,这6个空间自由度可以自由组合和分解,构成三维空间内的所有运动。

图3 一般物体的空间6DOF
将目标物体的质量、质心位置和质心惯性张量等质量属性与初始速度、初始角速度等运动状态通过用户自定义函数(UDF)编译的方式完成输入。进而通过6DOF求解器监测物体质心位置的变化来获得物体的位移。每个时间段的位移变化量Δs除以时间变化量Δt为该时间段内的速度,每个时间段内速度变化量Δvj除以时间变化量Δt为该时间段内的垂向加速度。根据牛顿第二运动定律,水作用在物体上的垂直力可以通过求解以下公式得到:
(6)
(7)
Ftotal=Mg-Fw=Ma
(8)
式中:vj表示物体的垂向速度;s表示物体的垂向位移;a表示物体的垂向加速度;i表示瞬时位移或时间的先后顺序;Ftotal表示物体受到的总垂向作用力;M表示物体的质量;g为重力加速度,g=9.81 m/s2;Fw表示水作用在物体上的垂向作用力。
2 数值模型与网格设置
2.1 网格划分与边界条件
计算模型为某型双机身飞机,其双机身设计增大了飞机的运输质量。飞机长度L为5.0 m、宽度D为5.8 m、高度H为2.0 m,飞机的质量为365.122 kg,将飞机的质心位置移动至计算域的坐标原点。飞机水上迫降时抬高机头一定角度滑翔迫降,飞机的三视图如图4所示。

图4 飞机三视图
图5为外流场计算域的边界条件设置,计算域是一个10L×8L×5L的长方体,除计算域正上方的边界条件是设置为pressure-outlet(压力出口),剩余5面的边界条件都设置为wall(壁面)。计算初始状态时,飞机底部刚刚与水面接触。
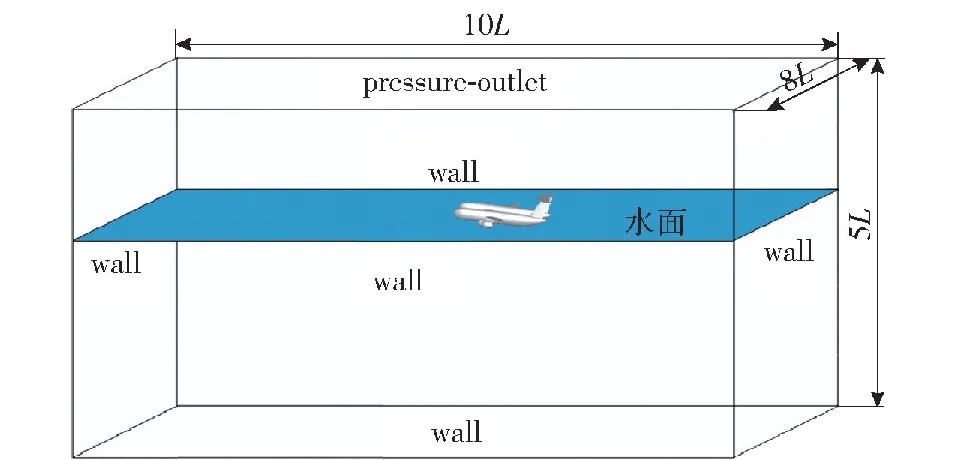
图5 边界条件
图6展示了计算域内的网格划分情况。为实现弹性光顺模型和结构重构模型等动网格方法,计算域内全部采用四面体类型网格。在飞机的周围生成一个球体移动网格区域,并对该区域的网格进行加密,便于准确地模拟飞机运动过程的数值变化以及更精确地捕捉飞机入水时周围的水花现象。将飞机设置为刚性移动物体,周围的球体移动网格区域设置为被动刚性移动区域,该区域在重力的作用下跟随飞机一起移动,与飞机有相同的运动状态,且内部网格不发生重构。

图6 整体网格区域和移动网格区域
考虑到外流场计算域内的初始压强分布对于非定常数值模拟的数值影响较大,因此需要在非定常数值模拟前对计算域内的流场分布进行预处理,将预处理后的稳定流场作为非定常数值模拟的初始流场。图7(a)为经过预处理后的压力分布云图,这里水下流场的压强分布符合以下压力公式:

图7 预处理后压力云图和相位云图
pa=ρwgh
(9)
式中:pa为相对压力;ρw为水的密度,ρw=998.2 kg/m3;h表示水的深度;操作压强为标准大气压101 325 Pa。图7(b)展示了水-空气介质的相位分布云图,空气的体积分数为0,水的体积分数为1,水和空气交界处的体积分数位于0和1之间。
2.2 网格收敛性验证
对整体网格区域和移动网格区域的网格单元尺寸以及体网格加密程度进行设置与调整,绘制 4种不同网格数量的网格,4种不同网格的详细信息如表1所示。分别采用4种网格对飞机以俯仰角度6°进行水上迫降数值计算,对比并分析其数值计算结果。
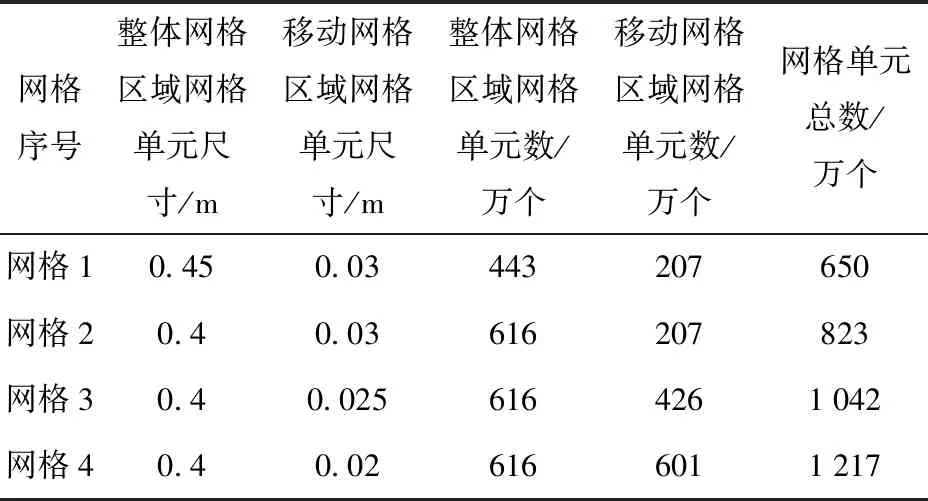
表1 4种不同网格的详细信息
计算结果如图8所示,图8(a)、图8(b)、图8(c)和图8(d)分别为采用4种不同网格计算得到的飞机水平速度、垂向速度、水平位移和垂向位移随时间的变化曲线对比。经过比较曲线的变化趋势可以看出:网格1和网格2的水平速度、垂向速度、水平位移以及垂向位移均与网格3和网格4的数值计算结果存在较大的差距,而网格3和网格4的数值结果的变化趋势基本吻合,其数值误差很小且在可接受范围内。综合考虑到计算精度、计算效率与计算资源,本文将采用网格3完成后面的数值计算与研究。
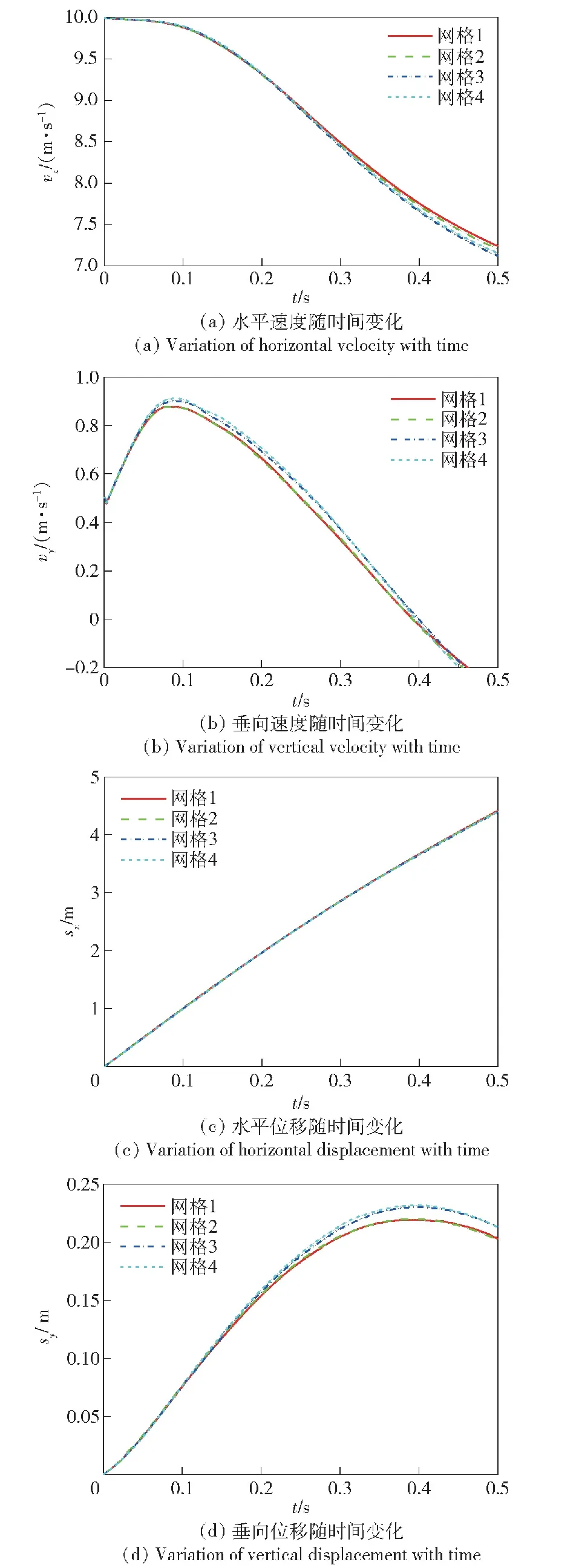
图8 不同网格的数值结果对比
3 算例验证
图9展示了圆盘的几何特征:一个厚度h=2.75 mm、半径R=50 mm的圆盘模型有一个入水速度U和旋转速度Ω,其中n为垂直于圆盘表面的单位矢量法线。圆盘的姿态由入水攻角α定义,ez为未受干扰的水面的单位法向量;圆盘的运动方向由冲击角β定义,ex为与水面相切的单位矢量。圆盘与水的碰撞过程通过高速摄像机记录。圆盘水漂实验采用铝制圆盘进行,圆盘与水的密度比为ρs/ρw≈2.7。

图9 圆盘的几何特征
为验证数值方法的准确性,对文献[8]水漂实验中入水速度U=3.5 m/s、入水攻角α=35°和速度攻角β=20°实验工况下的有旋转(Ω=65 rot/s)和无旋转(Ω=0 rot/s)圆盘水漂运动过程进行数值模拟。参照文献[24],由于圆盘在水漂过程中高速自旋,姿态角α在整个碰撞过程中保持不变,在数值模拟过程中只放开ez方向与ex方向平移自由度。
图10、图11所示分别为圆盘在有旋和无旋状况下的仿真结果与实验拍摄结果[8]对比。由图10和图11可以看出,仿真结果获得的不同时刻(时间间隔Δt=8.9 ms)液面喷溅形态和圆盘运动姿态均与实验拍摄结果吻合较好。图12展示了β=20°时不同α值的圆盘最小投掷速度vmin。从图12中可以看出:本文算例采用VOF方法数值计算得到的结果相比于Yan等[24]采用SPH方法数值计算得到的结果更贴合Yan等的理论结果,且本文算例采用的基于VOF方法的数值计算结果与Yan等的理论结果误差均小于4%,因此可以充分证明本文采用的数值方法符合数值计算精度要求。

图10 圆盘水面滑跳实验和数值计算的滑跳姿态对比(Ω=65 rot/s,上为实验结果,下为数值模拟结果)

图11 圆盘水面滑跳实验和数值计算的滑跳姿态对比(Ω=0 rot/s,上为实验结果,下为数值模拟结果)

图12 β=20°时不同α值的圆盘最小投掷速度对比曲线
4 飞机水上迫降数值模拟
4.1 计算模型
如图13所示,飞机的自身轴线与水面形成一个夹角α,定义该夹角α为飞机水上迫降时的入水俯仰角度。为研究不同俯仰角度α对水上迫降过程的影响,分别设置6°、8°、10°、12°、14°共5组俯仰角度。初始状态时,飞机尾部与水面刚刚接触,其水平初始速度为10 m/s,方向水平向左,竖直初始速度为0.5 m/s,方向垂直水平面向下。飞机不同俯仰角度的质量属性如表2所示。

表2 飞机不同俯仰角度的质量属性
图13 俯仰角度
4.2 计算结果与分析
采用第3节验证过的CFD数值计算方法对飞机水上迫降过程进行仿真模拟,并对比不同俯仰角度情况下飞机在水上迫降过程中的数值变化与流场分布情况。图14给出了俯仰角度为6°的飞机分别在t=0 s、t=0.1 s、t=0.2 s和t=0.3 s时的飞机姿态与水面变化情况。从图14中可以看出,该数值方法能够很好地捕捉飞机在水上迫降过程中的边缘喷溅现象。

图14 不同时刻的飞机姿态和水面变化(上为飞机姿态云图,下为水面变化云图)
图15展示了不同俯仰角度的飞机在不同时刻的相位云图。从图15中可以看出飞机在不同时刻的姿态、位置、水面变化以及底部浸水情况:除了俯仰角度为6°的情况以外,其他俯仰角度在t=0.1 s时,发动机均未触碰到水面;随着时间的推进,俯仰角度为12°和14°的飞机在迫降过程中发动机底部均没有完全浸入水中,而飞机尾部则全部浸入水中;从飞机尾部的浸水情况可以看出,飞机在整个迫降的过程中,垂向位移随着俯仰角度的增大而增大,即飞机以较大俯仰角度入水的垂向位移更大。

图15 不同时刻的相位云图(上为飞机侧面相位云图,下为飞机底部浸水相位云图)
图16展示了飞机俯仰偏转角度随时间的变化曲线。从俯仰偏转角度的变化趋势可以看出,在迫降过程中,飞机先低头后抬头,其俯仰角度变化是由于飞机在迫降过程中受到的俯仰力矩造成的。经过对比分析可以看出,飞机的俯仰偏转角度变化量随着俯仰角度的增大而减小,即飞机以较大俯仰角度入水时的偏转角度变化幅度越小,飞机不会大幅度抬头,飞机的俯仰稳定性越好。

图16 俯仰偏转角度随时间的变化
图17分别给出了不同俯仰角度的飞机在不同时刻的压力云图。从图17中可以看出不同时刻的飞机底部压力分布情况:在t=0.1 s时,俯仰角度为6°的飞机发动机因最先触碰到水面,底部会产生较大的压力;俯仰角度为14°的飞机最先触碰到水面的部位在机尾比较靠后的位置,飞机底部靠后的部位会产生较大的压力,随着迫降过程的进行,飞机底部的压力逐渐减小且最大压力区域向飞机前部移动;俯仰角度为14°的飞机发动机在t=0.2 s之前未接触水面,发动机底部的压力很小,最大压力区域一直在机身尾部位置。由此可以推断出:飞机底部的压力分布与飞机底部的浸水情况有关,最大压力区域均为飞机的浸水边界,即飞机刚接触水面的部分其压力值最大。

图17 不同时刻的压力云图
图18分别给出了飞机在不同俯仰角度情况下水上迫降的垂向速度和垂向位移随时间的变化曲线。由图18可以看出,飞机的垂向速度呈先增大后减小的趋势,飞机的垂向位移呈先增大后缓慢减小的趋势。分析飞机的垂向速度和垂向位移变化趋势的原因,可以得出:在飞机水上迫降过程的初期,水对飞机的垂向作用力小于飞机自身重力,飞机的垂向速度不断增大,垂向位移也随之增大;随着垂向位移的增大,水对飞机的垂向作用力逐渐增大,当飞机的垂向作用力等于飞机自身重力时,飞机的垂向速度达到峰值;随着时间的推进,飞机的垂向作用力继续增大并大于飞机自身重力时,飞机的垂向速度开始减小,飞机的垂向位移也逐渐减小并趋于平缓。

图18 垂向速度和垂向位移随时间变化
随着俯仰角度的增大,飞机的垂向速度峰值越高,垂向速度达到峰值所需要的时间越长,飞机的垂向位移越大。当飞机以俯仰角度14°入水时,飞机的垂向速度从0.5 m/s最高增大到1.28 m/s,垂向速度增大了156%。而飞机以俯仰角度6°入水时,飞机的垂向速度从0.5 m/s最高增大到0.9 m/s,垂向速度增大了80%。因此可以得出:飞机以小俯仰角度完成迫降,垂向速度的变化幅度较小,相同时刻的垂向位移越小;相反,飞机以大俯仰角度完成迫降,垂向速度的变化幅度大,相同时刻的垂向位移越大。
图19分别给出了飞机的水平速度和水平位移随时间的变化曲线。由图19可知:飞机的水平速度随时间变化逐渐减小,其减小幅度先缓慢后快速再缓慢;俯仰角度越小,水平速度减小得越快,相同时刻的水平位移越小。由于飞机水上迫降过程最终需要完全停靠在水面上,即飞机的水平速度减小到 0 m/s,飞机以小俯仰角度完成迫降可以在较短的时间内完成水面停靠。

图19 水平速度和水平位移随时间变化
图20分别给出了飞机在不同俯仰角度情况下受到的垂向作用力和垂向加速度随时间的变化。由图20可知:飞机在迫降过程中,水对飞机的垂向作用力的变化呈先增大后减小的趋势,在水上迫降后期垂向作用力会在一个相对稳定的数值期间上下波动;飞机在入水砰击过程中,随着飞机垂向位移的增大,飞机的浸水面积逐渐增大,因此飞机的垂向作用力也逐渐增大;随着飞机俯仰角度的增大,飞机受到的垂向作用力峰值越大,且到达峰值点的时间越长;飞机以14°俯仰角度入水,飞机受到水的垂向冲击载荷最高达到了6 555.025 N,是飞机自身质量的1.83倍;飞机以6°俯仰角度入水,飞机受到水的垂向冲击载荷最高达到了4 988.928 N,是飞机自身质量的1.39倍。因此,飞机以大俯仰角度进行水上迫降对飞机的结构强度要求更高;垂向加速度变化的趋势是先减小后反向增大再减小,在水上迫降后期垂向加速度也会在一个相对稳定的数值期间上下波动;飞机的俯仰角度越大,垂向加速度的变化幅度越大。
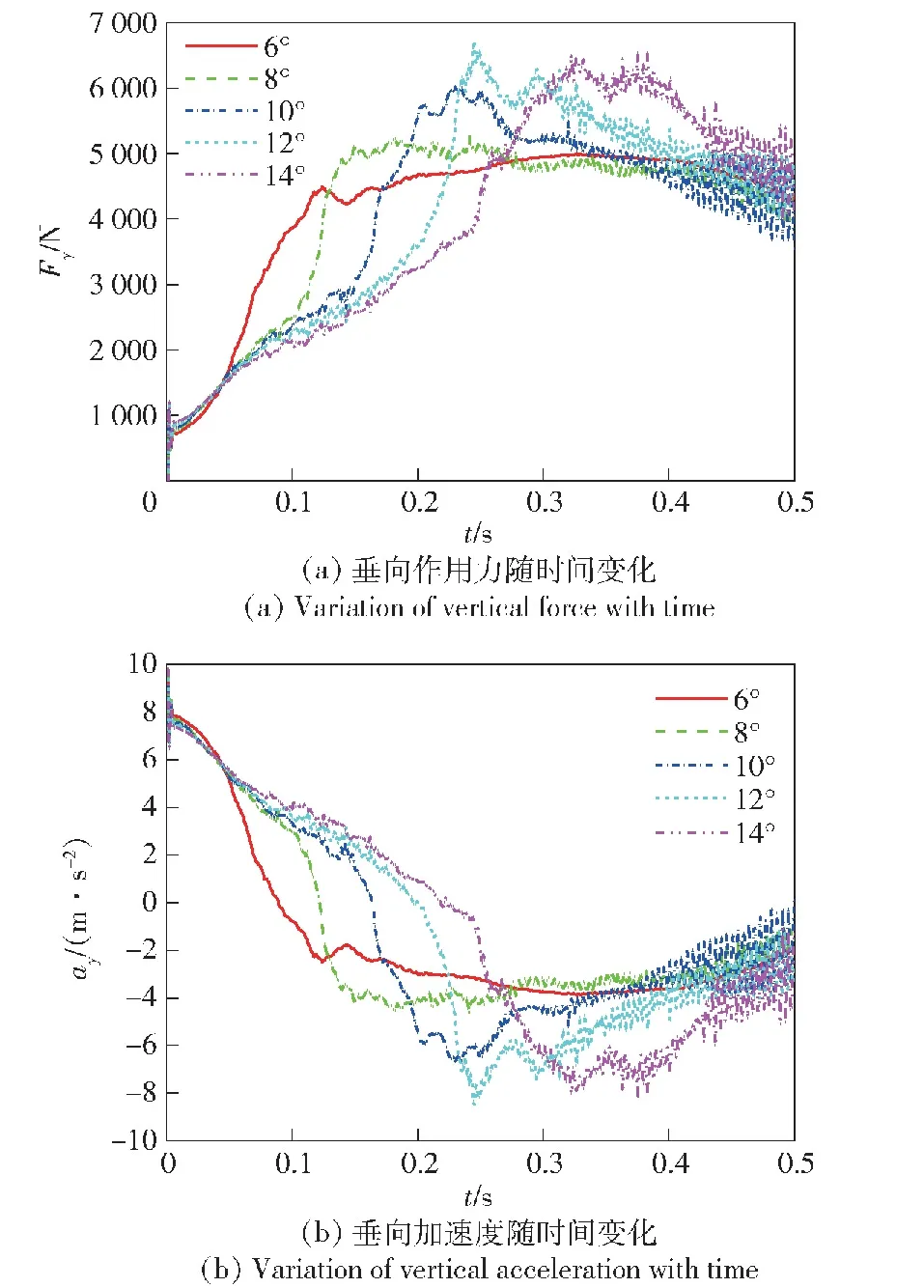
图20 垂向作用力和垂向加速度随时间变化
图21分别给出了飞机在不同俯仰角度情况下水平作用力和水平加速度随时间的变化曲线。由图21可知:飞机在迫降过程中受到的水平作用力呈先增大后减小的趋势,因此飞机的加速度也呈先增大后减小的趋势;随着飞机俯仰角度的增大,飞机受到的水平作用力峰值减小,水平加速度峰值也越小;飞机以6°俯仰角度入水时,飞机受到水的水平作用力较大,其加速度峰值和波动幅度都比较大,因此飞机的水平速度减小得更快,从而证实了飞机以小俯仰角度完成迫降可以在较短的时间内完成停靠的结论。

图21 水平作用力和水平加速度随时间变化
5 结论
1)在飞机水上迫降过程中,飞机因受到的俯仰力矩的作用会先低头后抬头,飞机的俯仰偏转角度变化量随着飞机俯仰角度的增大而减小,即飞机以较大俯仰角度入水时的俯仰偏转角度越小,俯仰稳定性越好。
2)在飞机水上迫降过程中,飞机底部的压力逐渐减小且最大压力区域向飞机头部移动。飞机底部的压力分布与飞机底部的浸水情况有关,最大压力区域为飞机的浸水边界,即飞机刚接触水面的部分压力值最大。
3)在飞机水上迫降过程中,俯仰角度越大,飞机的垂向速度峰值越大,飞机的垂向位移越大。即俯仰角度越大,飞机的浸水位移越大,飞机在水上迫降过程需要更深的浸水位移才能使飞机完全停下来。
4)在飞机水上迫降过程中,俯仰角度越小,飞机的水平速度减小得越快,飞机的水平位移越小。即飞机以小的俯仰角度完成迫降可以在较短的时间内完成水面停靠。
5)在飞机水上迫降过程中,俯仰角度越大,垂向作用力和垂向加速度的变化幅度越大,飞机受到的垂直作用力和垂直加速度的峰值越大;飞机以较小的俯仰角度完成水上迫降时,飞机受到的水的垂向作用力影响较小,垂向加速度变化幅度较小。
6)在飞机水上迫降过程中,俯仰角度越小,水平作用力和水平加速度的变化幅度越大,水平作用力峰值越大且达到峰值所需要的时间越长;飞机以较大的俯仰角度完成水上迫降时,飞机受到的水的水平作用力影响较小,水平加速度变化幅度较小。
7)该型双机身飞机在水上迫降过程中,俯仰角度越大,飞机受到的水的垂向作用力影响较大;俯仰角度越小,飞机受到的水的水平作用力和俯仰力矩影响较大。考虑飞机在迫降过程中需以较快的时间停靠下来,俯仰角度取6°比较合理;综合考虑飞机在迫降过程中水平方向、垂直方向以及俯仰方向的稳定性,俯仰角度取10°~12°比较合理。
综上所述,本文可为飞机水上迫降和跨介质飞行器入水砰击等问题提供参考价值。
