基于嵌入式离散裂缝模型的增强型地热系统热—流—力—化耦合分析

韩东旭 张炜韬 焦开拓 宇 波 李庭宇 巩 亮 王树荣

1. 北京石油化工学院机械工程学院 2. 中国石油大学（华东）新能源学院 3. 西安交通大学动力工程多相流国家重点实验室

4. 中国空气动力研究与发展中心低速空气动力研究所 5. 浙江大学能源高效清洁利用全国重点实验室

0 引言

地热能是储存在地壳中的一种稳定可再生能源，可应用于发电、供暖、工业和农业生产等多个方面。地热资源可以分为浅层地热、水热型地热和干热岩等。据估计，全球范围内埋深3.0～10.0 km的干热岩资源蕴藏的热能为全球石油、天然气和煤炭储藏能量的30倍[1]。我国干热岩资源量为2.52×1025J，约占世界资源总量的1/6，其中埋藏地下3.0～5.0 km深度的干热岩资源量为我国化石能源的80倍[2-4]。由于干热岩储层地质条件的差异性和复杂性，以及现有储层改造技术的“不可复制”性，造成其开发难度大[5-6]。目前，我国地热能的利用主要以水热型为主，高温干热岩的开发仍处于探索研究和发展阶段。

在对深部干热岩热能开发中，需采用人工压裂的方式提高储层内的导流能力，即在低渗透性储层建造高渗透性的人工裂缝，形成增强型地热系统（Enhanced Geothermal System，EGS）。不同于常规/非常规油气藏的“取物”过程，地热能开采为“取热”过程。在人工压裂过程中，EGS注采循环井会出现工质“注不进，采不出”的问题，实质是裂缝导流能力不足或裂缝网络沟通半径不够，导流能力不足是流、热、力和化等因素造成的裂缝开度变化的综合结果，裂缝网络沟通半径不足是热及形变诱导应力对岩体的剪切破裂和裂缝的起裂、扩展的综合影响[7]。而在长期取热过程中，冷流体从注入井注入后，工质在裂隙岩体中以渗流的形式流向采出井，并将储存在岩体中的热量提取出来。在此过程中，因温度变化产生的热应力会导致岩体变形，同时，在渗透压力和温度的共同作用下，岩体中矿物溶解/沉淀会缓慢改变流体通道，即EGS储层是一个典型受热—流—力—化综合作用的系统。所以有必要针对EGS开展热力、水力、岩体变形以及水—岩反应（Thermal-Hydraulic-Mechanical-Chemical，THMC）耦合机理的综合研究。

目前，国内外学者已经做了大量相关实验研究：在多场耦合作用方面，针对固—热耦合作用下花岗岩的力学、渗流特性进行实验，指出岩体力学性质变化是高温热破裂和石英晶格相变导致，如水力压裂、热压裂、化学刺激等储层增产的方法，实际是在改变储层的渗透率[8]。Kamali等[9]通过对热—流—力—化多场耦合作用下的裂缝渗透率和孔径变化进行测试，发现卸载时裂缝渗透率和孔径不完全恢复，升高注入流体的温度会提高裂缝恢复百分比。Yang等[10]对花岗岩进行冷热处理后，测试了热—流—力耦合参数，如导热系数、渗透率、Biot系数等，建立了参数预测模型，预测结果与实验吻合很好。由于实验室使用的岩体试样多为地表或浅层地下采集，即使取自深部岩体，也存在扰动应力的影响，且实验室多为高温冷却后的性质测试，很难将深部地层高温高压环境实时结合[8]。赵阳升[11]认为岩体力学特性在实验室尺度与实际工程特征尺度之间存在尺度效应和时间效应，实验室力学参数应用于岩体变形分析时，折减系数取值差异会导致工程变形预计存在很大偏差。

针对实验研究上的上述缺陷，数值模拟作为EGS研究的有效手段之一，与实验研究相互补充，对于干热岩储层的开发、方案制定、运行优化等有重要意义[12]。EGS储层由基岩和裂缝共同组成，是一种人工地热系统。针对裂隙岩体，常用的裂缝表征模型有等效介质模型、双重孔隙介质模型和离散裂缝模型（Discrete Fracture Model，DFM）。相比于前两者，DFM能够更加准确地描述裂缝的分布和走向，该模型适合以裂缝为主要渗流通道的裂隙岩体。Song等[13]通过COMSOL软件，基于DFM对其所提出的多分支井的EGS开发方式进行了热—流两场的数值模拟；Sun等[14]针对二维EGS储层，基于DFM建立了热—流—力三场耦合模型；Yao等[15]在考虑“局部非平衡传热”的基础上，基于DFM构建了EGS开发过程中三维热—流—力耦合模型，并对Desert Peak EGS 项目进行了模拟。

虽然DFM描述裂隙岩体具有较高的精度，但是当裂缝较复杂时，该模型需要大量的计算网格，很难在计算精度和计算成本之间做到平衡。为了解决这一问题，研究人员提出并发展了嵌入式离散裂缝模型（Embedded Discrete Fracture Model，EDFM）[16]。在该模型中，基岩和裂缝网格独立生成，裂缝网格降维嵌入到基岩网格系统中，裂缝和基岩之间的信息传递通过交换系数与传递系数进行。同DFM相比，EDFM使裂隙岩体的网格划分更加灵活，同时还兼顾了计算精度和计算效率。因此，近年来EDFM被越来越多的应用于裂隙岩体的数值模拟中。Wang等[17]提出了一种将EDFM和扩展有限元（The Extended Finite Element Method，XFEM）相结合的多场耦合策略，用于描述裂缝和多孔介质中的流动、变形和裂缝扩展。Sangnimnuan等[18]基于EDFM开发了非常规油藏中两相流—力耦合模型。Tran等[19]基于EDFM和改进的Bandis模型，求解了流动—溶质运移—诱导应力—断裂力学的耦合问题。Li等[20]基于EDFM和XFEM框架，建立了EGS的热—流—力耦合模型。此外，Xu等[21-23]也基于EDFM或改进的EDFM对复杂裂缝型储层中的流动、传热和传质进行了数值模拟。

尽管近几年，学者们基于EDFM在裂隙岩体流—力、流—力—化、热—流—力的耦合建模方面，以及针对复杂裂缝型储层的模拟计算方面取得了进展，但是还缺少基于EDFM的热—流—力—化四场耦合模型研究。因此，本文基于EDFM框架，建立了增强型地热系统的THMC耦合模型，采用有限体积法（Finite Volume Method，FVM）和XFEM相结合的方式进行求解，并对二维增强型地热系统储层中的流场、温度场、离子浓度场和位移场的时空演化过程及不同参数影响进行模拟与分析。

1 模型构建

1.1 EDFM模型

Li[24]首先提出了EDFM模型，随后Moinfar等[25]和Tene等[26]对其进行了发展。在该模型中，裂缝降维嵌入到基岩网格中，基岩和裂缝网格在几何上几乎完全独立，如图1所示。在实际物理问题中，为了实现基岩和裂缝、裂缝和裂缝之间的物理性交互，包括质量、能量、浓度等，研究人员引入了两个关键参数：交换系数和传递系数，根据基岩和裂缝的连接关系对其进行计算[27]。基岩和裂缝之间存在4种连接关系[16]：①相邻基岩网格单元（M1、M2、M3、M4）之间的连接；②同一条裂缝相邻裂缝网格单元之间的连接（F1、F2、F3、F4、F5）；③裂缝网格单元与所在基岩网格单元之间的连接；④交叉裂缝段网格单元之间的连接。该模型能够实现对裂缝型储层采用结构化网格进行剖分，避免生成比较复杂的非结构化网格，能够降低计算成本。因此，本文基于该方法的思想，构建了描述EGS取热过程的流动、传热、变形和溶质运移的THMC耦合模型。

图1 二维嵌入式离散裂缝模型示意图

1.2 渗流模型

EGS的岩性大部分是渗透率极低的基地花岗岩，流体在储层中流动满足达西定律，其流动过程采用质量守恒方程和达西方程描述，二维平面上不考虑重力影响，基于EDFM的基本思想，基岩质量守恒方程为[16]：

第i条裂缝质量守恒方程：

式中上标m和fr分别表示基岩和裂缝系统；pm、pfr分别表示基岩和裂缝中的压力，Pa；ρf表示流体密度，kg/m3；ϕm、ϕfr分别表示基岩和裂缝的孔隙度；ct表示总压缩系数，Pa－1；μf表示流体动力黏度，Pa·s；k表示渗透率张量，m2；Qm-fri、Qfri-m、Qfri-frj分别表示裂缝到基岩的单位体积流量、基岩到裂缝的单位体积流量、裂缝j到裂缝i的单位体积流量，s－1；为确保守恒，基岩和裂缝间的流量交换满足V表示裂缝或基岩的网格单元体积，m3；Qw表示井源项，s－1。

1.3 换热模型

同样基于EDFM思想，采用两套能量守恒方程分别描述基岩系统、裂缝系统以及它们之间的能量交换，并认为流体和基岩之间处于局部热平衡状态[29]。

基岩能量守恒方程：

第i条裂缝能量守恒方程：

式中T表示温度，℃；v表示渗流速度，m/s；cpf表示流体比热容，J/(kg·℃)；(ρcp)eff表示有效物性参数；λeff表示有效导热系数，W/(m·℃)；Efri-m表示裂缝i到基岩的能量交换，W/m3；Efri-frj表示裂缝j到裂缝i的能量交换，W/m3，Ew表示井源项，W/m3。

1.4 力学模型

基于线弹性小变形假设，考虑孔隙压力、热应力变化影响，忽略惯性项和体积力后，岩体受力本构方程为：

式中σ表示柯西应力张量，Pa；λ、G分别表示第一、第二拉梅系数，Pa；α表示Biot系数；βT表示热膨胀因子，Pa/℃；I表示单位张量；p0表示参考压力，Pa；T0表示参考温度，℃；ε表示柯西应变张量，；u表示位移矢量，m。对裂隙岩体的变形问题进行计算时，裂缝两侧的位移不连续，属于强不连续问题，而XFEM能够有效地求解强不连续问题，位移求解采用下式[30]：

式中上标 FE、H、tip 和 J 分别表示常规单元、贯穿单元、裂尖单元及交叉单元（图2）。

图2 XEFM 结点加强方式图

1.5 化学模型

化学模型包括两部分，一部分描述矿物离子在储层中的运移和扩散，另一部分描述储层中的水—岩反应。矿物离子在储层中运移和扩散通过溶质运移方程描述，基岩的溶质运移方程为：

第i条裂缝的溶质运移方程为：

式中C表示溶质浓度，mol/m3；D表示扩散系数，m2/s；ψfri-m（或ψm-fri）、ψfri-frj分别表示基岩与裂缝间的离子浓度交换、裂缝与裂缝间的离子浓度交换，mol/(m3·s)；为确保守恒，基岩与裂缝间的离子浓度交换满足Mw表示井源项，mol/(m3·s)；Qr表示化学反应源项，Qr=ϕrnρs，mol/(m3·s)；ρs表示矿物密度，kg/m3；rn表示化学反应速率，mol/(kgw·s)。

EGS中流体与岩石的化学反应速率极低，一般遇到的反应类型为表面控制的化学反应，同TOUGHREACT模拟软件一样，本文应用的是Lasaga提出的化学反应速率方程[31]：

式中下标n表示矿物索引；kn表示矿物反应速率常数，mol/(m2·s)；An表示矿物反应比表面积，m2/kgw；Qn表示矿物离子活度；Keq平衡常数；θ、η由实验决定。矿物反应速率常数与温度相关，采用Arrhenius的形式描述：

式中k25表示25 ℃下的速率常数，mol/(m2·s)；Ea表示活化能，J/mol；R表示气体常数，J/(mol·K)；T表示绝对温度，K。

由水—岩反应造成的储层中基岩和裂缝的孔隙度变化通过下式确定：

式中ϕ0表示储层初始时刻的孔隙度；Ms表示矿物摩尔质量，kg/mol。孔隙度的变化对渗透率的影响通过Kozeny-Carman方程确定：

式中k0表示储层初始时刻的渗透率，m2。

2 数值方法

上述数学模型中包括p、T、u、C等4个未知变量，涉及流场、温度场、力场、浓度场的求解，各场求解过程中相互耦合，相互作用，耦合过程设置如下：①在流场求解中，耦合基岩和裂缝的能量守恒方程、溶质运移方程和水—岩反应方程，依赖于温度变化对流体密度、黏度的影响以及溶质运移和水—岩反应对储层渗透率、孔隙度的改变；②在温度场求解中，耦合基岩和裂缝的质量守恒方程、溶质运移方程和水—岩反应方程，依赖于压力场变化对渗流速率的影响以及溶质运移和水—岩反应对储层渗透率、孔隙度的影响；③在化学场求解中，耦合基岩和裂缝的质量守恒方程、基岩和裂缝的能量守恒方程，依赖于压力场变化对渗流速率的影响以及温度变化对流体密度、黏度的影响；④在力场求解中，考虑渗流压力和温度变化对储层变形的影响，因此其求解是在热、流、化三场求解收敛基础上进行。

数值求解时，首先采用FVM求解基岩和裂缝的渗流场，获得压力场的解（pm，pfr），再求解基岩和裂缝的达西方程，获得速度场的解（vm，vfr）；然后，采用同样方法求解基岩、裂缝的能量守恒方程，获得温度场的解（Tm，Tfr）；将得到的流场的解和温度场的解带入溶质运移方程和水—岩反应中，求解得到矿物离子浓度场的解（Cm，Cfr）；最后采用XFEM求解力平衡方程，获得位移场的解（u）。每个时层采用顺序迭代耦合策略，求解流程和求解方法如图3所示。

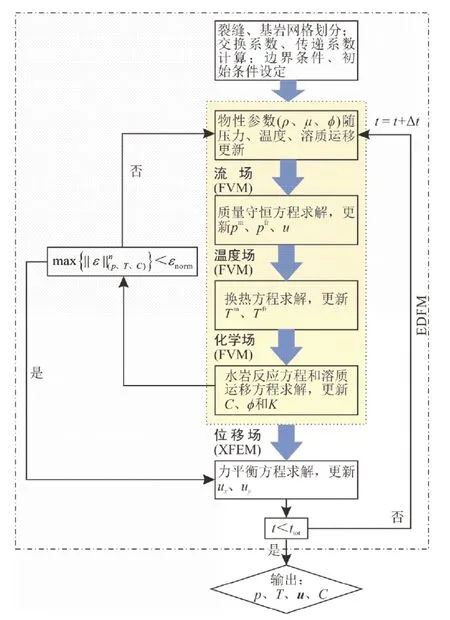
图3 THMC耦合求解流程图

3 模型验证

本文建立THMC耦合模型是在本文参考文献[20]所建立THM耦合模型的基础上添加了化学模块，关于THM耦合模型及数值方法验证已在文献中进行了详细描述，在此不再叙述。由于化学反应及矿物离子的运移受储层温度、流体流动影响较大，因此本文将获得的压力场、温度场、离子浓度场的解与MRST[32]中Fully Resolved Solution Method（简 称FRSM）在细尺度网格上获得的解进行对比。区别于EDFM的裂缝处理方法，FRSM以裂缝宽度作为网格单元的离散尺寸对整个计算域和裂缝进行剖分，然后分别对基岩和裂缝所在的网格单元定义其物理属性。

所用物理模型尺寸和裂缝位置如图4-a所示，模型尺寸设定为10 m×5 m，裂缝宽度设定为0.04 m。两种方法得到的计算域网格划分结果如图4-b和图4-c所示，采用FRSM划分计算域获得的基岩和裂缝细尺度网格数为31 250，采用EDFM划分网格获得的计算域基岩网格数为20 000，裂缝网格数为209。

图4 两种方法的网格划分图

模型左边界模拟注入井，纯水注入，注入压力为1.5 MPa，注入温度为20 ℃，右边界模拟生产井，开采压力为0.1 MPa，其余边界为非渗透、绝热边界。初始压力为0.1 MPa，初始温度为180 ℃。假设储层矿物离子在运移扩散之前处于平衡状态，同时储层中矿物离子以二氧化硅为主，扩散系数为1.0×10－9m2/s，矿物离子的初始浓度为3.8 mol/m3，基岩和裂缝的渗透率、孔隙度、密度等参数与本文参考文献[20]保持一致。时间步长取0.1 d，总模拟时间365 d，储层中温度变化和溶质运移求解是在储层压力场分布稳定的基础上进行，计算结果如图5所示。可以看到，本文基于EDFM计算的压力场、温度场、浓度场与采用FRSM在细尺度网格上获得的计算结果基本一致。恒定注采压力下采用EDFM和采用FRSM计算的生产井温度最大相对误差为0.71%，平均为0.70%，溶质浓度相对误差最大为0.4%，平均为0.12%，采用EDFM计算用时为2 652 s，采用FRSM计算用时为3 650 s，前者用时较后者减少了27.3%，证明本文采用的模型和数值方法具有可行性。

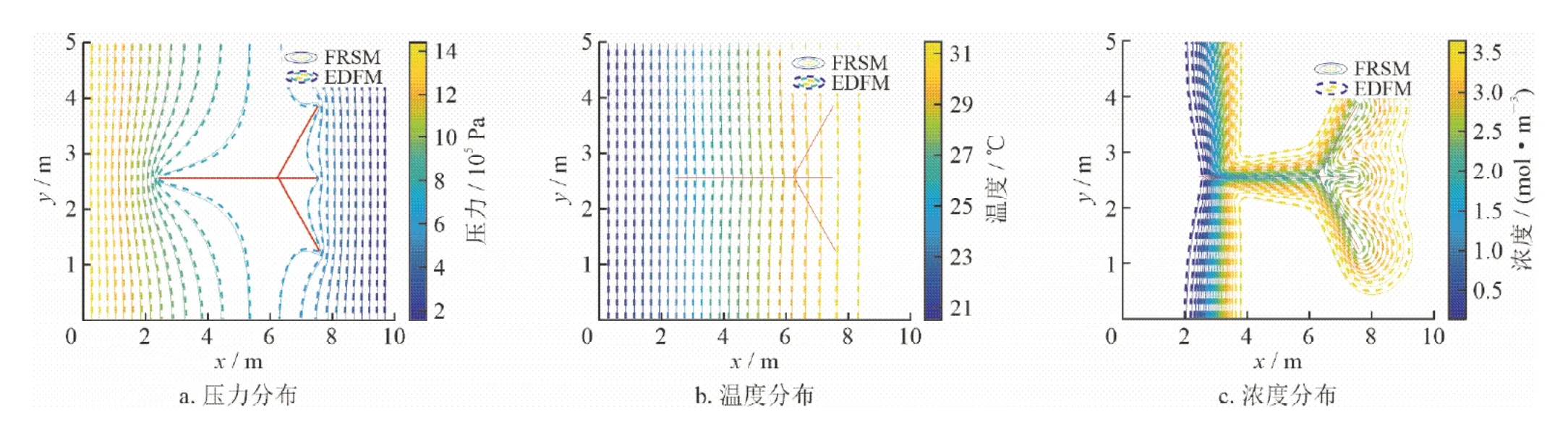
图5 两种方法的数值解对比图

4 数值算例

在EGS长期取热过程中，储层中的渗流压力、温度、矿物离子浓度和岩体随时间发生变化，为明晰其时空演化规律，应用所开发和验证的THMC四场耦合模型及程序进行模拟。本文设置算例主要用于检验模型和计算方法的可行性，暂仅考虑注入流体与储层中的矿物石英相互作用。石英在水溶液中发生水解反应而溶解生成硅酸（H4SiO4），或者其等价形式Si(OH)4，采用下式[33]：

式中，正反应过程表示矿物溶解，逆反应过程表示矿物沉淀。由式（9）可知，矿物化学反应中除了确定反应速率常数外，还需要确定矿物离子活度与给定温度下平衡常数的比值。本文石英水解反应速率常数k25、反应活化能Ea参考文献[34]选取，不同温度平衡状态下石英的溶解度采用下式[35]：

式（14）可以确定温度在0～300 ℃时饱和水压下的石英溶解度。

采用五点布井方式，即一个注入井周围分布4个开采井，反之亦然。考虑所有井的流场呈对称分布，笔者取五点开采区域的1/4进行研究。注入井压力为15.5 MPa，注入温度为60 ℃，生产井压力为4.77 MPa，四周边界为非渗透、绝热、位移约束条件，矿物离子浓度梯度为0。储层初始压力为5.0 MPa，初始温度为236 ℃，石英占储层总矿物体积分数为66%。对于储层中孔隙度和渗透率的非均匀性，采用高斯随机分布和Carman-Kozeny 经验式生成[36-37]（图6）。储层初始孔隙度分布为3.5%～4.5%，平均值为3.99%。初始渗透率分布为0.17～0.38 mD，平均值为0.26 mD。储层岩石物性参考恰卜恰地热田设置[38]，部分参数有改动，具体见表1。在取热过程中，注入水的密度、黏度随温度、压力不同而发生变化，图7给出了水的密度、黏度随温度、压力的变化情况[39]。其中，图7-a两条黑色实线与边界围成的区域表示压力在4.77～15.5 MPa、温度在20～236 ℃时，流体密度的变化情况；图7-b两条黑色实线与边界围成的区域表示在相同压力和温度范围下的流体黏度的变化情况。

表1 模型主要参数表

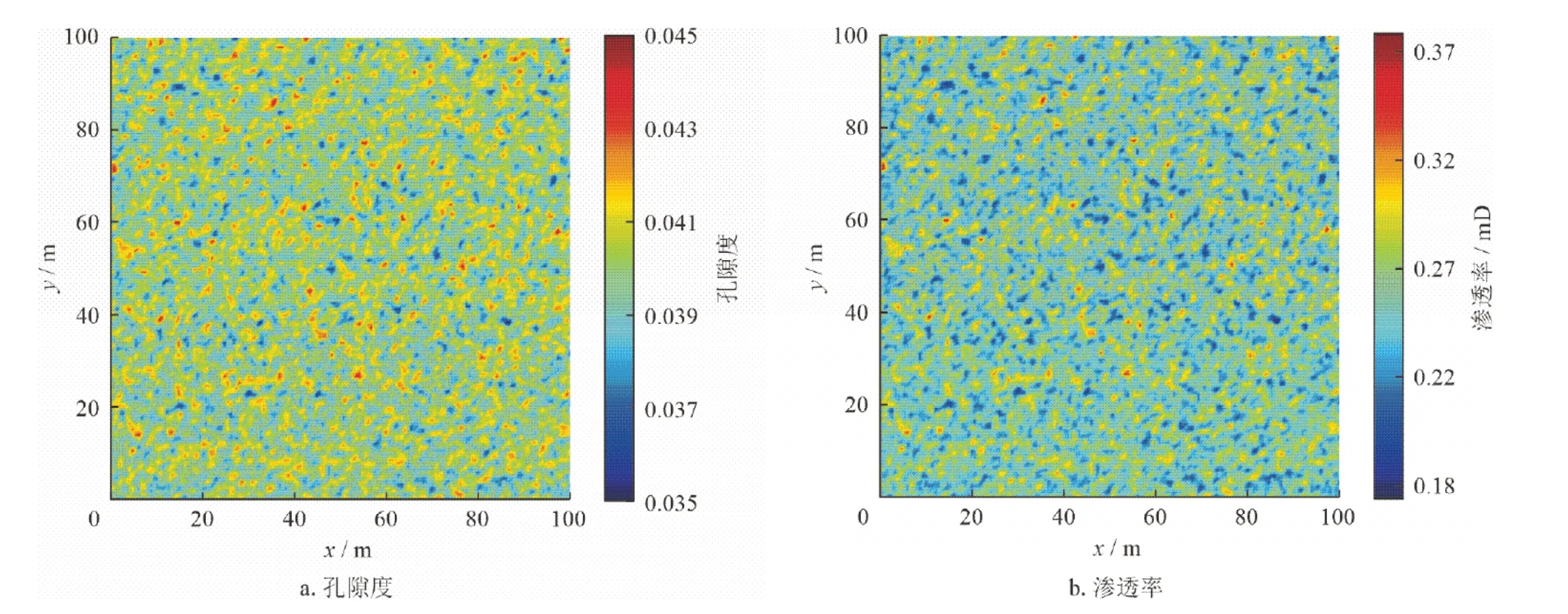
图6 储层孔隙度和渗透率非均匀分布图

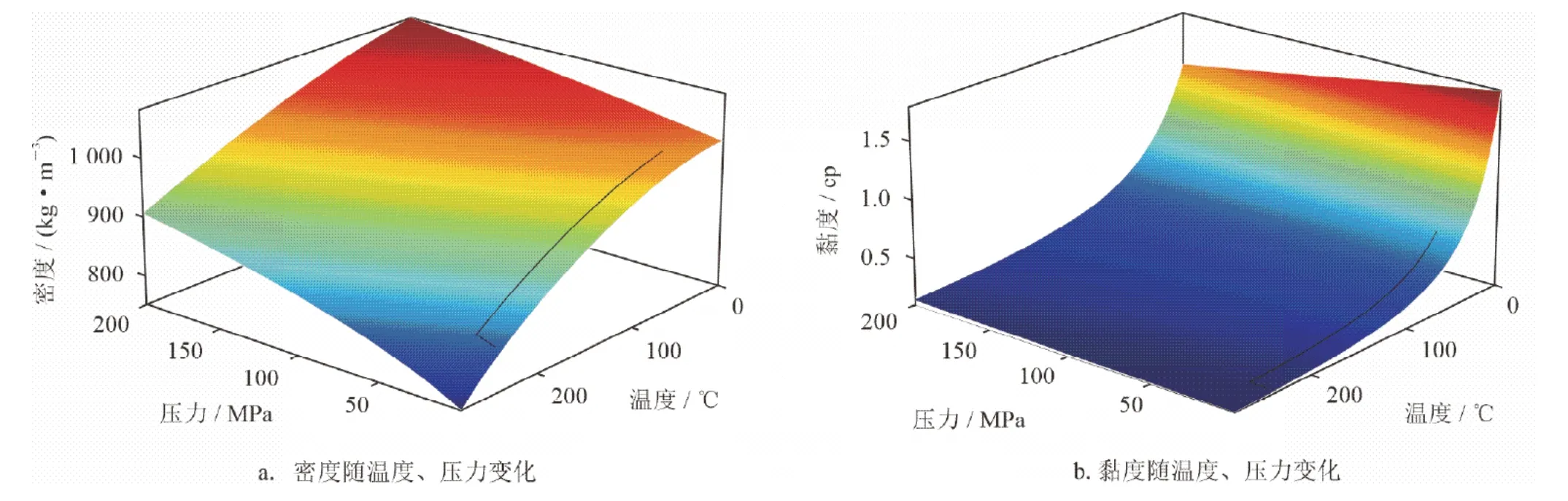
图7 水的密度、黏度随温度、压力变化图

所用二维裂缝型地热储层几何模型如图8-a所示，左下角绿色图标表示注入井，右上角红色图标表示生产井，注入井和生产井之间由人工裂缝贯穿，储层共预置裂缝70条。基于所设置的模型参数对不同网格数量下的开采温度随开采年限变化进行计算，结果如图8-b所示，可以看出当计算域网格数增加到24 820个单元继续增加时，开采温度基本不随网格数量变化而变化。故本文采用该网格划分方案进行计算域离散，结果如图8-c所示，其中，基岩网格数为22 801，裂缝网格数为2 019。

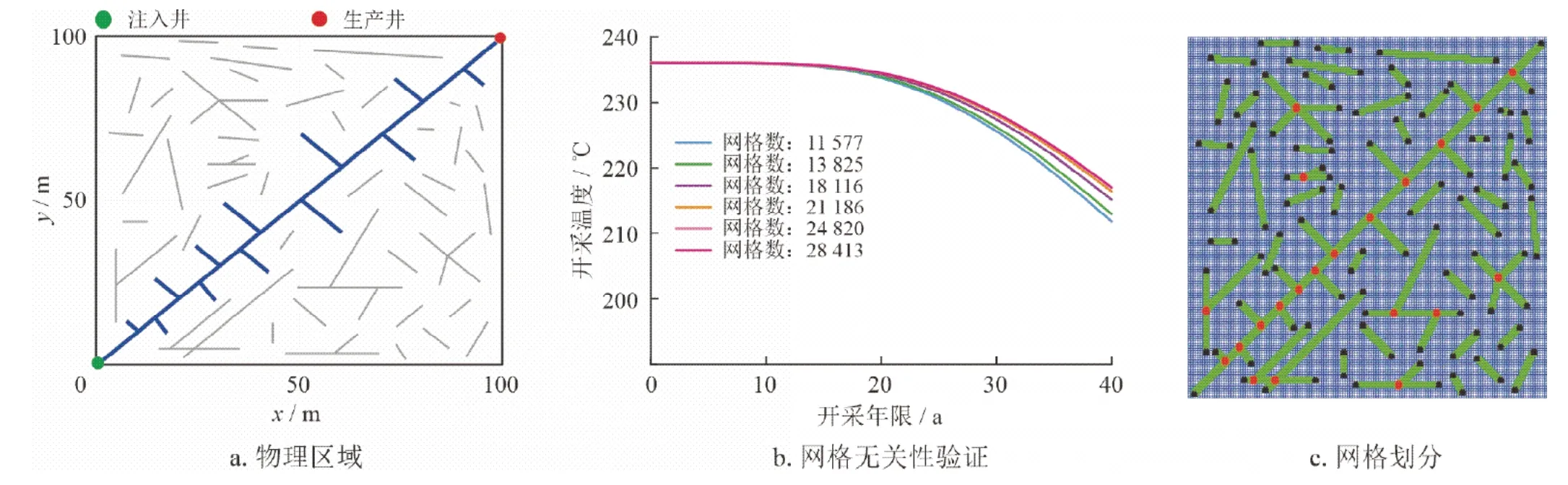
图8 裂缝型储层模型和网格划分示意图

4.1 演化规律

注入压力可改变储层中流体的渗流速率和孔隙压力，而渗流速率会影响流体与储层高温岩体的对流换热、矿物离子的运移，因此有必要对恒定注入压力下储层中压力场的时空演化进行分析。图9-a展示了系统运行40年过程中3种不同年份储层中渗流压力空间分布。可以看到，裂缝作为储层中流体渗流的主要通道，使储层中的压力分布呈现非均匀性。因为裂缝介质渗透率大，渗流速度较快，基岩系统渗透率小，渗流速度滞后，因此裂缝介质中的压降较快。在裂缝介质与基岩系统水力交换影响下，裂缝介质附近基岩系统的压降也较快。当注入井和生产井之间存在贯穿裂缝时，这种影响更加明显；同时，还可以发现随着冷流体不断注入，注入井附近的温度下降，流体的黏滞性增强，流动阻力增大，表现为随开采年限增加，注入井附近的压力梯度逐渐增大。

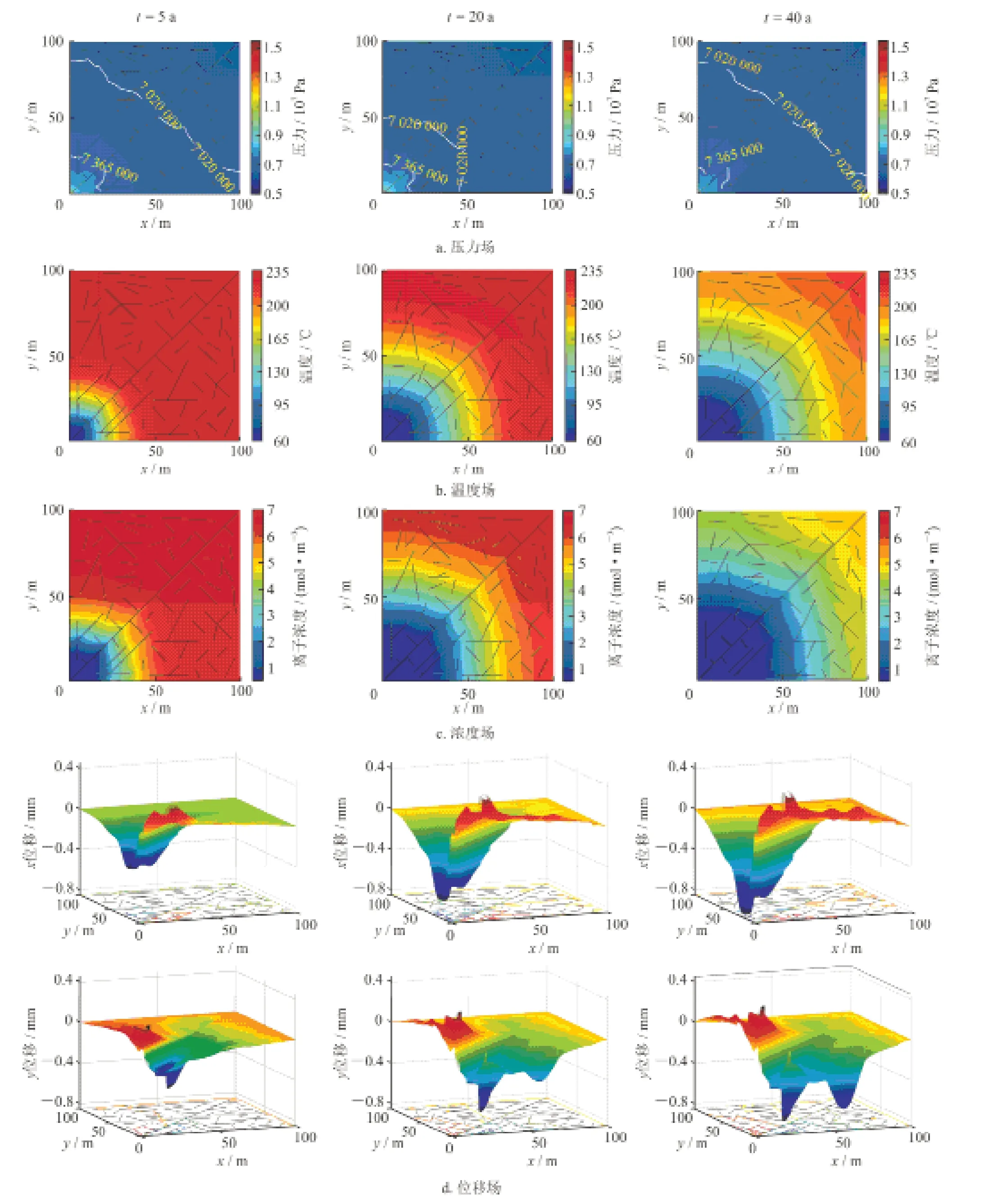
图9 储层中压力场、温度场、浓度场和位移场随时间演化规律图

储层中的温度不仅对流体的密度、黏度产生影响，而且还对水—岩反应速率产生影响，同时温度变化产生的热应力变化也会导致储层中的岩体变形，产生位移变化。图9-b展示了系统运行40年过程中3种不同年份温度场的空间分布。可以看到，在恒定注入压力下，冷流体不断被注入，开采初始阶段受导热和对流换热作用，注入井附近的低温水与高温基岩发生热量交换，水温升高，而高温基岩的温度下降，随着开采年限增加低温区域逐渐扩大，此时开采井附近岩体温度变化缓慢，在热突破形成之前，系统可维持较长时间的高热量输出；由于裂缝中流体渗流速度高于周围基岩，裂缝介质中热对流明显，沿着渗流方向在裂缝附近岩体的温度变化较快，尤其是注采井之间存在贯穿裂缝时，该现象更加明显；此外，需要指出的是虽然储层部分区域裂缝密集，但是由于这些裂缝并未完全贯穿，因此在这些裂缝附近流体与高温岩体的对流换热作用体现并不明显。

在长期取热过程中，储层中水—岩反应产生的矿物离子会随着流体渗流而运移、扩散，储层中矿物离子运移、扩散会打破储层内矿物离子固有的平衡状态，导致在储层不同位置将发生矿物离子的溶解和沉淀反应，使储层中的孔隙度随之改变，反过来影响流场和温度场。图9-c展示了系统运行40年过程中3种不同年份储层矿物离子浓度空间分布。可以看到，储层中矿物离子浓度分布趋势与温度变化趋势比较类似，两者都受流体对流作用影响，同时温度分布还会直接影响水—岩反应强弱，储层温度高的区域，矿物溶解速率大，矿物离子浓度高；但是不同于温度场的变化，受溶质扩散系数影响，在裂缝及附近区域矿物离子浓度分布明显低于周围基岩系统，裂缝对储层中矿物离子运移、扩散作用明显。

储层中渗流压力、温度、化学溶蚀长期作用会导致储层岩体发生变形、产生位移变化，高温岩体变形会造成储层结构颗粒脱落、裂缝渗透性改变等。图9-d展示了系统运行40年过程中3种不同年份储层岩体产生的x方向位移和y方向位移空间分布。可以看到，随着开采时间的增加，x方向位移和y方向位移的区域范围和最大值都在增加。当储层中不断注入流体时，孔隙水压力会改变，孔隙水压力作用于裂缝面从而使岩体有效应力降低，导致裂缝介质的法向张开度发生改变，同时高温岩体也会因温度下降而发生收缩，裂缝面在热应力作用下进一步张开，储层中x方向位移和y方向位移主要集中在裂缝面附近。此外，在温度、注入压力发生较大梯度变化的区域，如注入井附近，越易产生较大的位移。

4.2 影响因素分析

本节主要从储层岩石参数、注水参数两个方面，分析各参数变化对EGS取热的影响，其中储层岩石参数包括基岩渗透率、裂缝渗透率和裂缝开度；注水参数包括注水压力和流体物性。

4.2.1 储层岩石参数

图10-a展示的是不同基岩渗透率对应的开采温度变化，模拟时其他参数保持不变，选用非均匀分布渗透率的最大值、最小值和平均值进行对照。可以看到，在开采前10年中，四种不同基岩渗透率对应的开采温度都能保持稳定的高温度输出，随后逐年下降，并且基岩渗透率越大开采温度下降越快，当系统运行第40年时，基岩渗透率为0.17 mD时对应的开采温度下降了15℃，单位厚度开采井的净取热功率由1.86 kW降为0.85 kW，而基岩渗透率为0.38 mD时对应的开采井温度下降幅度增大了10.6%，单位厚度开采井的净取热功率由3.5 kW降为1.26 kW。可见，储层低渗透率虽然能够维持较长年限较高的开采温度，但这并不表明储层渗透率越低越好，因为低渗透率会造成流体流动缓慢，储层中的开采井质量流率减小，净采热功率降低，同时还可能造成流体通道堵塞，影响系统运行。

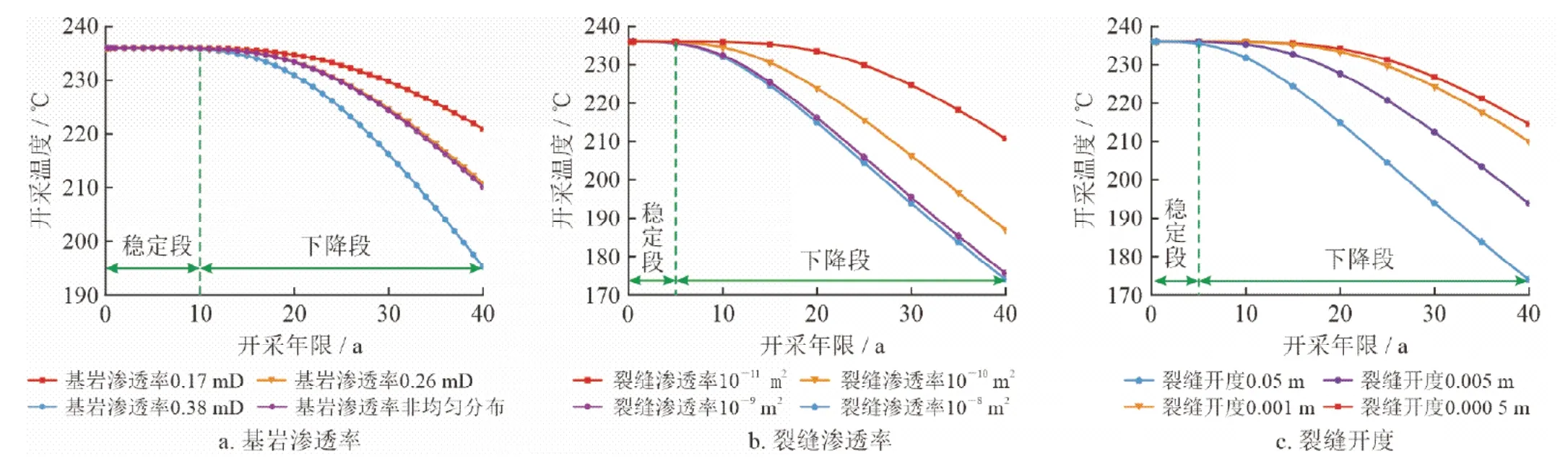
图10 储层岩石参数对取热温度影响图

同样，保持其他参数设置不变，模拟改变裂缝渗透率、裂缝开度对开采温度的影响，结果如图10-b和图10-c所示。可以看到，4种不同裂缝渗透率和裂缝开度都可使系统维持一定年限稳定的高温度输出，但是这种稳定的高温度输出时间比改变基岩渗透率获得的时间要短。可见，改变裂缝参数比改变基岩参数对开采温度的影响强烈。而在开采温度下降阶段，当系统运行第40年时，裂缝渗透率由10－9m2继续增大到10－8m2时，前者相比于后者，开采温度和单位厚度开采井的净取热功率分别仅高了2 ℃和0.01 kW；裂缝开度由0.000 5 m增大到0.001 m时，前者相比于后者，开采温度仅高了4 ℃，单位厚度开采井的净取热功率方面仅低了0.05 kW。可见，当裂缝渗透率在较大范围内变化或者裂缝开度在较小宽度范围内变化时，其对开采温度和净取热功率的影响变弱。

4.2.2 注水参数

一般来讲，注入流体参数与当地工程条件紧密相关。为了研究注入流体参数对开采温度的影响，本文分别模拟了注水压力和注入流体物性对开采温度的影响，其他参数设置不变，结果如图11所示。可以看到，两种情况下开采温度均先维持约10年的稳定阶段，然后出现不同幅度的下降阶段。当系统运行第40年时，开采压力由9 MPa、12 MPa、14 MPa增大到15.5 MPa时，对应的开采温度分别为229.1 ℃、221.8 ℃、215.5 ℃和210.1 ℃，如图11-a所示。可见，注入压力越大，随着开采时间增加，开采温度降低越快。注入压力改变注入流体的渗流速率，影响其取热效率。当开采压力由9 MPa增大到15.5 MPa，系统运行第40年时，单位厚度开采井的净取热功率前者比后者低54%。

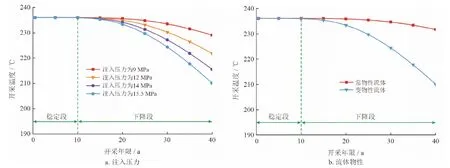
图11 注水参数对取热温度影响图

模拟过程中，假定注入流体的密度、黏度不随储层的温度、压力变化而变化，与初始值保持一致，即选用常物性流体注入时，在温度下降阶段，开采温度随年限增加下降幅度较小，如图11-b所示。当系统运行到第40年时，采用常物性流体注入获得的开采温度为231.7 ℃，与采用变物性流体注入获得的开采温度相比，两者偏差22 ℃。分析可知，在给定注入流体物性时，变物性流体会因为储层的温度、压力分布不均而发生变化，结合图7可知，当压力恒定时，注入水的密度、黏度会随温度增大而降低。初始阶段受注入压力、温度和储层温度场的分布影响，注入流体物性变化对开采温度的影响较少，两者可维持一定年限稳定高温度输出。随着开采年限的增加，注入井附近的压力梯度逐渐增加，见图9-a。开采井附近仍旧维持较高的温度场分布，造成变物性流体在开采井附近黏度较低而渗流速度偏大，单位时间内输出的热量比常物性流体大，储层的温度下降快，使变物性流体计算的开采温度较常物性流体偏低。

4.3 水—岩反应影响

为探究EGS系统在取热过程中受化学反应的影响程度，利用热—流—力—化（THMC）耦合模型和热—流—力（THM）耦合模型模拟储层热开采过程中水—岩反应对开采温度的影响。水—岩反应中石英溶解速率参考文献[40]选取，其中，实验条件25 ℃、pH值为7时，对应的溶解速率为－10.4，其他参数设置保持不变，两种耦合模型模拟的开采温度随时间变化如图12所示。可以看到，两种耦合下热储层均可维持约10年稳定的高温度输出，但是在温度下降阶段，随着开采时间的增加，开采温度变化差别较大。当系统运行第40年时，THMC耦合下的开采温度为195 ℃，与THM耦合相比，两者偏差为15 ℃，偏差幅度为7%。水—岩反应对EGS储层中的孔隙度产生影响，由式（12）可知，孔隙度改变会导致储层固有渗透率发生变化，进而影响流体的渗流速率以及与高温岩石的对流换热效率。设置算例中储层孔隙度为非均质分布，平均孔隙度由初始的3.99%变为4.49%，孔隙度增大了12.5%。可见，在取热过程中，矿物石英的水—岩反应主要表现为溶解过程。此外，需要说明的是EGS人工热储中的花岗岩主要成分除了石英外，还包括碱性长石、斜长石、角闪石及云母等，这些矿物部分水—岩反应强度比石英更大，长期取热过程中对储层孔隙结构改变不可忽略。因此通过数值模拟研究EGS系统取热性能时，应该综合考虑储层各不同矿物化学反应造成的影响。

图12 水—岩反应对取热温度的影响图

5 结论

1）裂缝作为储层中流体的主要渗流通道，在恒定注采条件下，裂缝介质及其附近基岩系统的渗流压力、温度、离子浓度变化较快，当注采井之间存在贯穿裂缝时，该现象更加明显，而位移变化主要集中在裂缝面附近，在渗流压力、热应力梯度大的区域，如注入井附近，易产生较大位移。

2）基岩渗透率较低时，开采温度下降缓慢，EGS可维持较长年限的较高开采温度，但是渗透率较低时会造成储层中流体流动缓慢，开采井质量流率减小，进而影响净取热功率。裂缝渗透率或者裂缝开度发生改变时，EGS均可维持一定年限的较高温度稳定输出，随后出现不同幅度的下降，但是当裂缝渗透率增大到一定值或者裂缝开度减小到一定值时，改变裂缝参数对开采温度的影响减弱。

3）考虑注入流体物性随渗流压力、储层温度变化时，开采温度变化明显，模拟EGS运行40年时，采用变物性流体比采用常物性流体计算的开采温度偏低22 ℃。因此，对于实际储层取热分析时，需要考虑注入流体物性参数的影响。

4）EGS长期运行过程中水—岩反应会造成储层孔隙度改变，进而对开采温度产生影响，模拟EGS运行40年时，考虑水—岩反应比不考虑水—岩反应计算的开采温度偏低为15 ℃，储层平均孔隙度值增大12.5%。可见，长期运行的EGS水—岩反应的影响不可忽略。

本文通过自主编程，将所建立的THMC耦合模型和数值方法在二维EGS储层问题中进行了实施，相关方法和结论可为EGS多场耦合研究提供借鉴和参考，未来将考虑储层其他矿物组分的化学反应、力学变形对流热化三场影响的双向耦合并推广至三维问题中，为EGS储层的工程开发和利用提供一些准确、可靠的预测。