土壤干缩开裂三维模型构建及其参数敏感性分析

农 睿 ，万愉快 ，孙伯颜 ，孙振源 ，朱 磊

（1.宁夏大学土木与水利工程学院, 银川 750021；2.宁夏大学 宁夏回族自治区黄河水联网数字治水重点实验室，银川 750021）

0 引 言

在干旱条件下，土壤干缩开裂是在自然和人造物体破坏过程中可以观察到的最常见的物理现象之一[1]。水分蒸发产生的裂隙对土壤的力学性能和水力性能有显著影响，受到了农业、地质、环境及工程等学科研究者的广泛关注。裂隙网络为水和溶质运输提供了优先的流动路径，会显著增加土体的导水性[2]，从而增加地下水污染的可能性[3]。同时，裂隙破坏了土壤的完整性和稳定性，会导致土体强度受损、过度变形和压缩性增加等一系列问题[4]，对土方工程[5]、堤坝[6]、路堤[7]、工程屏障[8]的稳定构成重大威胁。此外，干燥裂隙的存在使得土壤表面粗糙度增加，加速了土壤风化和侵蚀，推动了局部或区域尺度沙尘暴和荒漠化的形成[9-11]。因此，对土壤干缩开裂进行系统研究，对于防治地质和岩土工程问题具有重要意义。

为了模拟土壤干缩开裂的发展过程，学者们已经建立了大量的土壤干裂数值模型[12-15]，但目前还缺乏关于裂隙深度的全面建模方法。土壤干缩开裂的数值建模方法主要分为有限元法（finite element method, FEM）、离散元方法（discrete element method, DEM）和线弹性断裂力学理论。VO等[16]采用水力-力学耦合和内聚裂隙单元的有限元程序，研究了黏土干缩裂隙的几何形状和发育过程，数值分析结果在水力扩散、裂隙萌生、收缩演化及干燥阶段时序方面与试验数据较为吻合。沈珠江等[17]基于FEM搭建了非饱和土简化固结理论数值模型，数值分析结果表明简化固结理论方法具有实用性。然而，由于需要预先定义少量裂纹或将模型边界作为潜在裂纹，FEM模拟对于裂隙产生和发育的预测能力较弱[18]。

DEM将土壤视为离散元的组合，在模拟干燥开裂方面具有良好的潜力[19]。PERON等[20]使用DEM对土壤的干缩开裂进行仿真，重现了细粒土壤裂隙的萌生、扩展和几何形状。AMARASIRI等[21]采用通用离散元代码（universal distinct element code, UDEC）对黏土的超固结现象进行建模，该模型可以捕捉到不同长度、高度和材料模具中包含的土壤裂隙演变特征。SIMA等[22]基于三维离散元方法搭建数值模型，分析了土基界面特性、试样厚度、收缩参数和微观力学参数等材料特性对黏土干缩开裂的影响。需要指出的是，传统离散元模型将离散单元视为刚体，无法预测干缩过程中的水分蒸发、热量和质量交换等多物理过程[19]。

在已有的研究中，KONRAD等[23]利用线弹性断裂力学理论构建了平均裂缝深度和间距预测框架，简要描述了裂纹扩展现象。VOGEL等[24]开发了一个基于Hookean弹簧网格的物理模型，以重现土壤裂缝模式的真实整体外观，模拟水分蒸发引起的裂缝动态拓展。与Konrad模型相比，它能捕捉到自然界中可观测到的裂缝网络发展非线性动力学的显著特征（即裂隙的特征形状和分叉的特征角度）。一般情况下，弹簧网络模型一个周期的仿真计算时间（即弹簧网络对节点的计算力和节点位置的更新）与模型的复杂性（即节点和弹簧的数量）成正比增加，而有限元模型的计算时间（即计算模型的边界条件和求解刚度矩阵定义的联立方程所用时间）则与节点数量的立方成正比[25]。因此，弹簧网格模型在模拟土壤开裂过程上可以节省大量计算时间。然而，Vogel模型只能再现土壤表面的裂隙形态特征，不能模拟裂隙弹簧网格沿深度的破坏，故需要进行三维弹簧网格建模。

研究裂隙沿深度产生与拓展的规律及机理对于研究土壤干缩开裂过程非常重要。但迄今为止，学界对土壤三维干缩开裂过程的研究较少，也鲜有考虑裂隙深度分布的土壤干缩裂隙数值模型，土壤表面下干燥裂隙的萌生和扩展过程尚不清楚。缺乏对土体内部开裂过程或三维开裂特征的认识，将阻碍对土体水力学行为作出准确评价。因此，为了模拟裂隙沿深度方向的形成与拓展，本文基于Vogel模型引入重力项，划分三棱柱状弹簧网格结构，并考虑土壤竖向弹性对裂隙深度的影响，建立三维土壤干缩开裂模型，通过Monte-Carlo模拟验证模型参数值与裂隙模式之间的关系，并通过最小化裂隙面积、长度、欧拉数密度和深度频率与实测值之间的差值来设定优化参数，最后分析模拟结果对纵向弹性系数的敏感性，以期为研究土壤弹性变化对裂隙深度的影响提供理论参考。

1 模型构建

1.1 三维模型重力项引入及三维弹簧网格划分

本文基于线弹性断裂理论[26]构建了三维土壤干裂模型，模拟因水分蒸发而导致土壤干燥开裂的动态。与Vogel模型不同的是，三维模型考虑了重力的作用，每个节点的重力被确定为重力加速度（g，固定为9.8 m/s2）和节点上的质量（mi）的乘积。模拟区域的土壤被划分为三棱柱（原为三角形）组成的弹簧网格结构，如图1所示。

如图1所示，节点间连接着长度为d和弹簧系数为K的弹簧，任意2 个相邻节点的应变εij，弹簧和重力所产生的合力Fi以及每个节点处的总能量Ei分别为[27]：

式中│xi-xj│代表网格中相邻节点间的距离，x=(x,y,z)T。d是弹簧的松弛长度，将其从初始值为1（完全松弛状态）逐渐减小来模拟土壤干缩开裂过程。K为弹簧的弹性系数，与土壤弹性有关。VOGEL等[24]将水平弹簧的K设置为1。当弹簧受力F大于摩擦力f时，节点才会移动，并且节点根据式（3）向能量最小位置移动，由式（2）可以求解节点新位置。此时判断节点应变是否大于弹簧临界应变，若满足上述条件，则弹簧断裂形成裂隙。通过弹簧的临界应变引入土壤的异质性，临界应变阈值是均值（））和方差（δ2）的高斯概率分布，在空间随机分布。边界条件指定为边界节点不允许垂直边界移动，这是线弹性断裂理论模型的前提条件[25]。

在本文构建的三维模型中，一个公共节点连接着n个相邻三棱柱，每个三棱柱结构的质量均匀分布在其6个节点上。且每个三棱柱结构的质量由土壤的密度（ρ）和结构的体积（V）求得，因此，节点i的质量可表示为

式中n表示由节点i连接的三棱柱结构，Vn是三棱柱n的体积。

1.2 土壤结构收缩特性

VOGEL等[24]模型中没有涉及时间的概念，但将弹簧张力u=1-d解释为时间或土壤含水率的函数。同时TANOUE等[25]观察到，黏土块的表面比内部干缩得更快。由于收缩速率的不同，膨胀应力导致土壤表面干缩开裂。为了描述这种现象，假设表层土壤（与空气直接接触）的弹簧结构处于不断收缩的状态。也就是说，表层土壤的弹簧松弛长度d1随着时间的推移而减小，减小步长即土壤脱水时间的离散化设置为10-4，减小至最小松弛长度d1min（代表土壤开裂程度）。而内部土壤的收缩率保持在初始值，即d2=1。

1.3 模型求解及裂隙深度提取

本文在CodeLite平台采用 C++语言编写程序代码进行计算求解，模型的模拟结果由平均临界应变、方差δ2、松弛参数nit、摩擦力f、纵向弹性系数Kz共同控制，其物理性质如表1所示。

表1 三维模型参数Table 1 List of parameters of the three-dimensional Model

图2展示了根据裂隙点坐标生成的三维可视化图像。图3展示了沿土壤深度分层的裂隙二值.tiff图像。该算例设置400×400×40个节点（代表100 cm × 100 cm× 10 cm的土壤体积）的长方体弹簧网格结构，2节点间隔为0.25 cm，均值和方差分别为0.1和0.20，摩擦力f为8×10-4。选取开裂时间为18 h的裂隙图像进行展示。如图3所示，裂隙面积、长度形态土表至深处呈现逐渐减小的变化特征。STEWART等[28]假设裂隙垂直于土壤表面发育，截面形态呈三角形或楔形。作为参考，该模型假设裂隙垂直于土壤表面发育，与试验中测量的裂隙竖向深度进行对比。读取每层的裂隙分布信息，筛选土壤表层裂隙点（以1表示），再逐层竖直对比裂隙点的变化，若在下层土壤中该裂隙点转变为非裂隙点（以0表示）则记录该点深度，循环结束后统计模拟裂隙的深度频率分布特征。

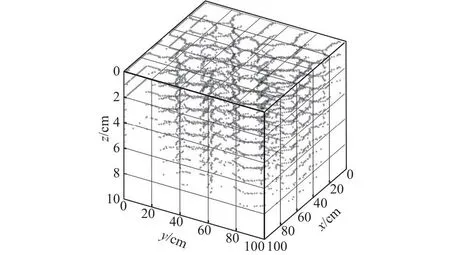
图2 三维裂隙图像可视化示例Fig.2 An example of visualization of 3D crack images

图3 模拟裂隙图像随土壤剖面不同深度（h）的变化趋势Fig.3 Variation trend of simulated crack image along different depth (h) of soil proile

2 案例分析

2.1 试验区概况

试验场地位于宁夏回族自治区吴忠市同心县（105°54'E, 36°58'N），地处鄂尔多斯台地南部黄土高原，属北温带大陆性季风气候区。干旱少雨，年平均降水272 mm，蒸发量大，年蒸发量2 325 mm。年平均气温8.6 ℃，多年平均日照3 024 h。土壤为粉质黏土，田间持水率质量分数为23.82%，0～50 cm土层平均容重为1.58 g/cm3，试验区土壤的物理性质如表2所示。

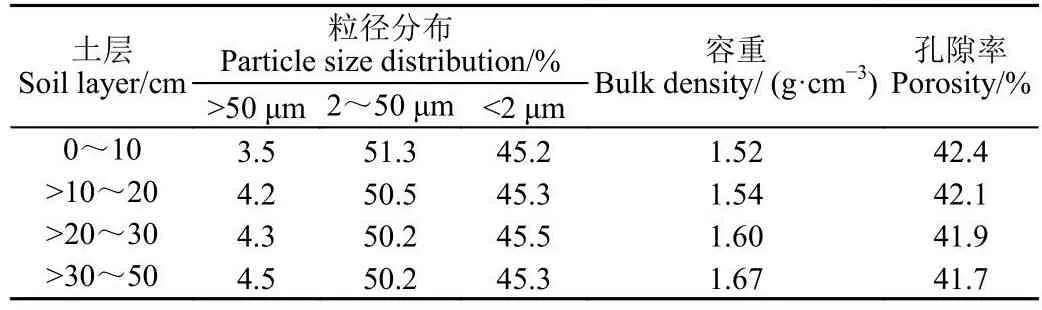
表2 试验区土壤物理性质Table 2 Soil physical properties in the test area

该试验于2022年8月在同心县试验区进行。前期调研发现，田间土壤裂隙平均最大深度小于10 cm。结合前人对农田裂隙特征参数的研究经验[29]，选取深度为10 cm，表面尺寸100 cm×100 cm的4个土壤长方体试验区作为研究对象，编号为S1～S4。试验前，对土体进行松动消除田间土壤的原有裂纹；随后于土壤表面施加积水，保持恒定的注水速率（2 L/s）。利用时域反射技术（time domain reflectometry, TDR）测量土壤含水率，以确保土壤在0 ~ 10 cm完全饱和。饱和时，土体表面膨胀而无裂隙，至此开始记录土壤收缩时间，使其自然脱水，期间日均温为20.0～32.0 ℃，空气湿度为43%～60%，试验过程中天气状况良好，无降雨。

运用Canon EOS 5DII数码相机（最高分辨率5 616×3 744像素）每隔2 h拍照记录裂隙形成和发育状况，试验时间为08:00-18:00，连续观测3 d。夜间采用防雨塑料铺设试验区，防止雨水降落和水分夜间蒸发。土壤开裂完全后，采用长为15 cm，直径为1.5 mm，测量精度为1mm的钢针测量裂隙竖向深度，将钢针分别依次插至裂隙底部。沿裂隙长度方向布置测量点，2个测量点的距离间隔均为1 cm，每个测量点重复测量5次并取平均值，每个试验区分别统计100个点。

2.2 基于图片的裂隙量化方法

2.2.1 土壤表面裂隙图像处理

为了深入研究表面裂隙模式的几何形态，采用以下4个步骤处理图像：1）将图像中的非试验区域裁切去除，并统一图像尺寸为1 024×1 024像素；2）将裂隙彩色图像转化为灰度图像；3）采用阈值分割法，将裂隙灰度图像转化为二值图像，若像素点的值大于阈值则划分为1，小于阈值划分为0。4）通过去噪去除二值图像中的杂质。以S1为例，处理前后裂隙图像对比如图4所示。

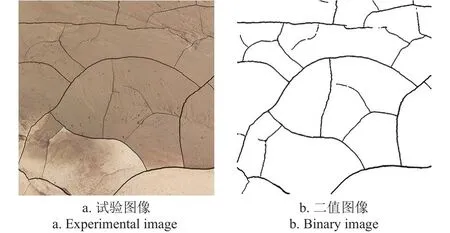
图4 试验区S1图像二值化Fig.4 Image binarization of experimental area S1

2.2.2 土壤裂隙网络量化方法

采用描述裂隙拓扑性质的Minkowski数（Mk） 量化土壤表层裂隙网络，其包含3个基本几何特征，即裂隙的面积（A，cm2）、长度（L，cm）和欧拉数（E）。对于二维表面裂隙，Mk（k=0，1，2）的计算式如下[30]：式中X表示黑色像素集合；δX表示结构X的边界；r是边界的曲率半径；ds表示边界单元；M0、M1、M2分别表示二维结构中裂隙的面积、裂隙的边界长度和结构联通性的拓扑度量。A(X)、L(X)、E(X)分别表示黑色像素集合X的面积、长度和欧拉数。欧拉数E定义为孤立对象的数量N（封闭凸）减去孔洞数H（封闭凹），即E=N-H，描述裂隙网络的连通性。

闵可夫斯基密度（Minkowski densities）可以用来衡量不同尺寸图像的裂隙结构特征，其计算式[30]如下：

式中Δ为图像面积；m0、m1、m2分别表示Minkowski面积密度、长度密度和欧拉数密度。

2.3 三维土壤干裂模型应用

选择S1试验区率定模型参数，包括均值、方差δ2、松弛参数nit、摩擦力f和纵向弹性系数Kx，S2～S4试验区进行模型验证。模型率定的目的是通过调整输入参数来捕捉现场记录的裂缝模式。本研究采用Monte-Carlo法率定输入参数，使用24个核（Intel Xeon Gold 6 226 CPU，运行频率为2.9 GHz，内存为256 GB）的工作站进行运算，按照1.3节进行模型求解和裂隙深度提取，与基于图片的裂隙量化方法计算的结果进行对比。

ZHU等[31]通过最小化试验和模拟的Minkowski密度差异来校准模型时间。本研究采用ZHU的方法，通过试验的4个时间点（4、14、24、34 h）对模型时间进行匹配，每个时间点对应模型中一定的弹簧松弛长度。通过式（8）对试验和模拟裂隙图像的Minkowski密度进行计算。在率定和验证过程中，采用决定系数（R2）、均方根误差（SRMSE）、一致性指标（SIA）和偏差（SBIAS）4个指标[32-33]对模拟结果Minkowski密度和裂隙深度频率的准确性和一致性进行检验，其中R2和SIA值越接近1、SBIAS和SRMSE越小表示模拟精度越高。一般认为，R2大于0.5，SRMSE在20%以内时模型达到率定要求[34]。

②出入线明挖段为三线矩形断面，结构断面宽度15～19m，托换梁需跨过明挖隧道，托换梁最大跨度达23.3m，工程施工难度大，实施风险高。

3 结果与分析

3.1 试验实测和计算结果

图5展示了S1～S4试验区裂隙Minkowski密度在4个时间点（4、14、24、34 h）的变化趋势。在土壤干缩裂隙随时间变化的过程中，由于裂隙不断产生与发育，面积密度、长度密度与欧拉数密度均呈现增函数的变化，这符合自然条件下干缩裂隙的发育规律[3]。随着裂隙继续拓展，土壤含水率减少，裂隙模式逐渐固定，长度密度的增长趋势随时间变缓，而面积密度仍在持续增大。

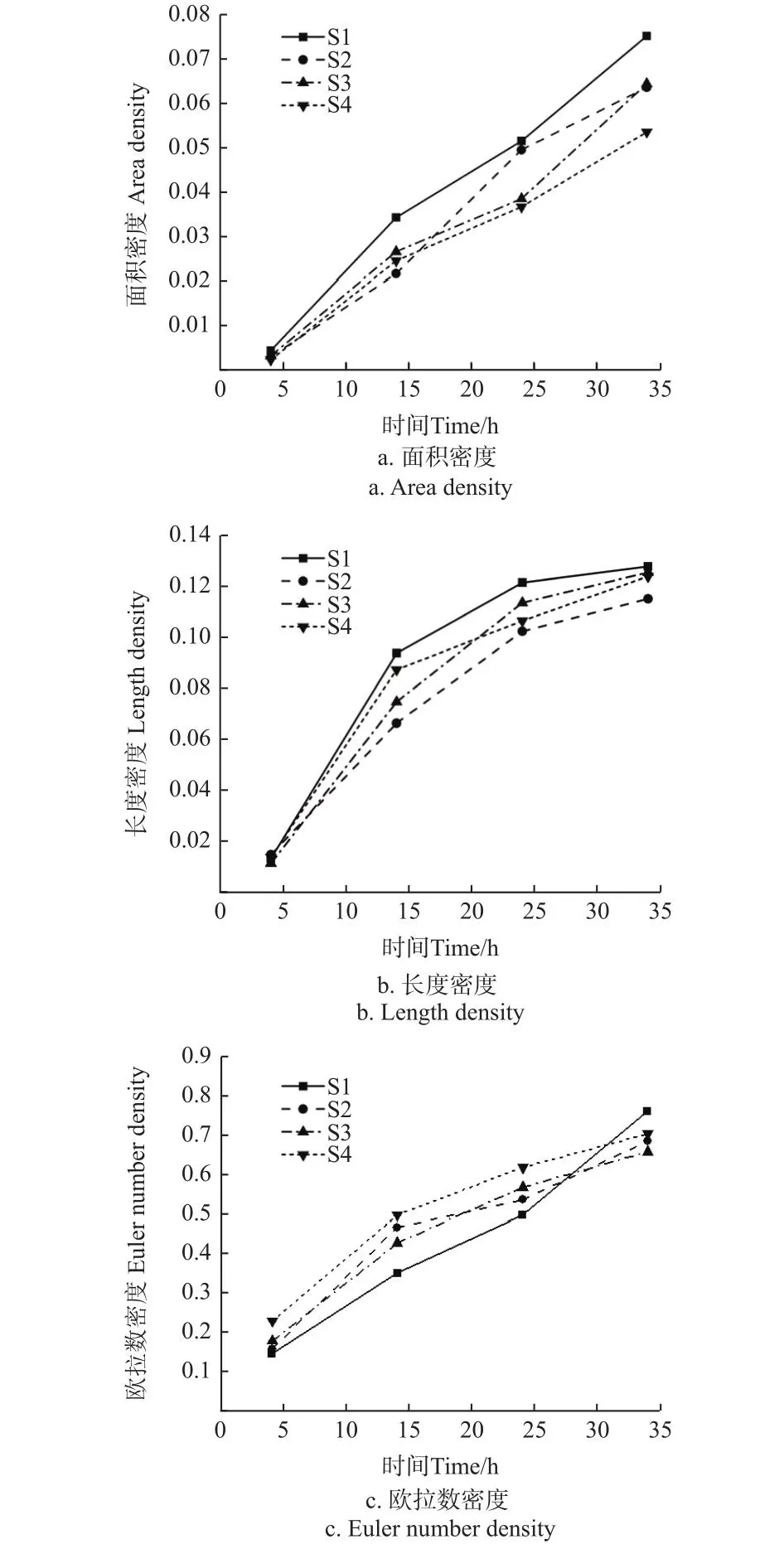
图5 试验区S1～S4裂隙Minkowski密度函数Fig.5 Minkowski density function of crack for experimental area S1-S4

通过钢针法测量了试验的裂隙深度，结果如图6所示。

图6 试验区S1～S4裂隙深度相对频率统计Fig.6 Statistics of crack depth relative frequency for Experimental area S1-S4

由图6可知，试验裂隙深度主要分布在土深1～6 cm。4次独立试验S1～S4的裂隙深度相对频率随土壤深度均呈现先增大后减小的趋势，但峰值及其所处深度不同，当到达各峰值后相对频率值均迅速下降。

3.2 模型率定结果

基于如表3所示初始值，根据Monte-Carlo仿真结果，计算各输入参数组合的评价指标，确定模型的参数率定值。

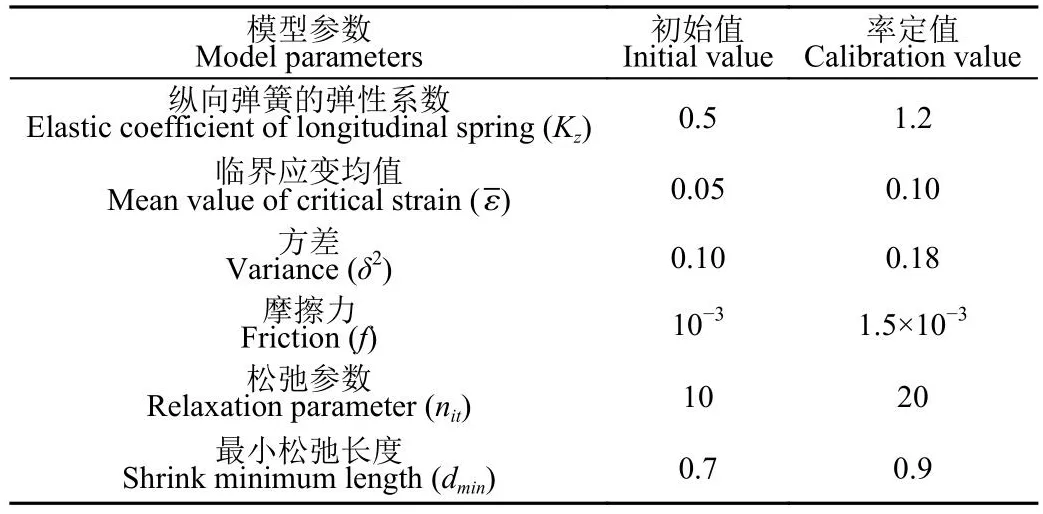
表3 三维土壤干缩开裂模型参数率定值Table 3 Parameter calibration values of 3D soil shrinkage cracking model

对比不同时间土壤表面试验与模拟裂隙图像图7，以及模拟裂隙图像与试验裂隙图像的Minkowski密度匹配情况图8，可以看出模拟与试验裂隙的Minkowski密度发展规律基本一致，4个时间点（4、14、24、34 h）的面积、长度、欧拉数密度值基本相同。对比土壤开裂结束后模拟与试验裂隙深度频率分布图9可知，裂隙深度（4～5 cm）的频率占比最大，深度（8～10 cm）的频率占比最小，试验与模拟的裂隙深度相对频率基本一致。量化率定结果如表4所示，模拟结果的R2均不小于0.944，SIA均大于等于0.986，SBIAS均小于等于0.103，SRMSE均小于等于0.052，可认为模型满足率定要求。

表4 模型率定的评价指标Table 4 Evaluation indicators of model calibration

图8 Minkowski密度试验值与模拟值比较Fig.8 Comparison between experimental and simulated values of Minkowski density

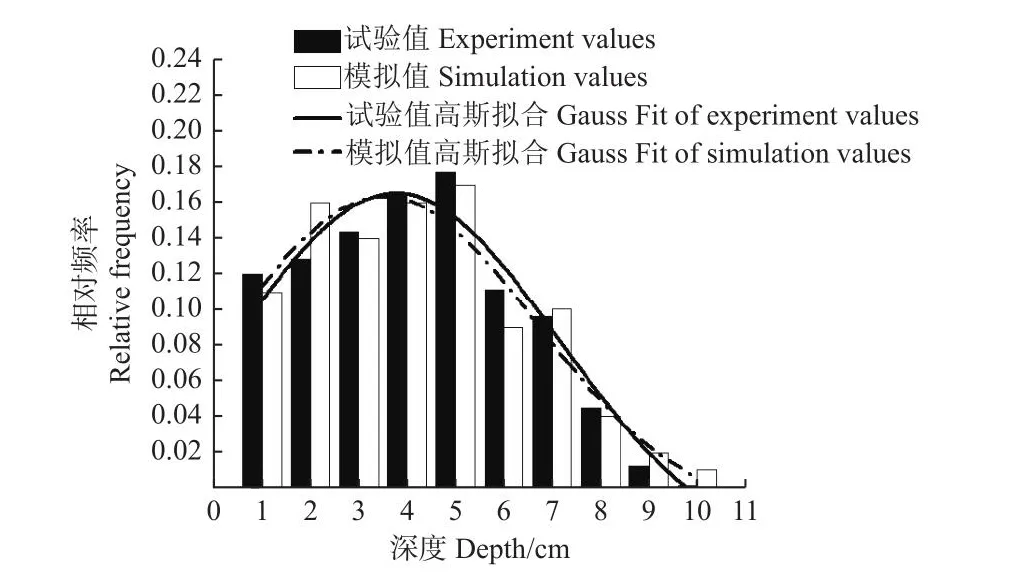
图9 裂隙深度试验值与模拟值比较Fig.9 Comparison between experimetnal and simulated values of crack depth

3.3 模型验证结果

通过试验区S2～S4的裂隙验证了模型参数的可靠性，在率定参数组合下，每组独立试验通过调整“随机种子数”生成100组土壤临界应变随机场，得到100组模拟图像。比较每组试验裂隙（Minkowski密度及裂隙深度频率）与对应100组模拟裂隙（Minkowski密度及裂隙深度频率平均值）间的差异，如表5所示。结果显示，S2～S4试验与模拟Minkowski密度和裂隙深度相对频率的R2在0.849～0.959之间，SIA为0.965～0.988，SBIAS为0.103～0.189，SRMSE为0.005～0.083。R2和SIA均大于0.8，SBIAS和SRMSE均小于0.19，总体模拟结果较好，可见，所构建模型的模拟结果较好，土壤表面收缩的假设与边界条件的设置合理，模型可靠性较高，能够应用于实际模拟。由图10可知，模拟裂隙深度为1～6 cm的占比为0.90，模拟裂隙深度为7～10 cm的占比为0.10，大部分裂隙的深度集中在1～6 cm之间。不同深度下裂隙试验与模拟结果的深度频率平均值基本一致，拟合线变化趋势和范围基本相同，表明构建的三维模型对于模拟土壤开裂结束后的裂隙深度频率分布特征具有较高的一致性。

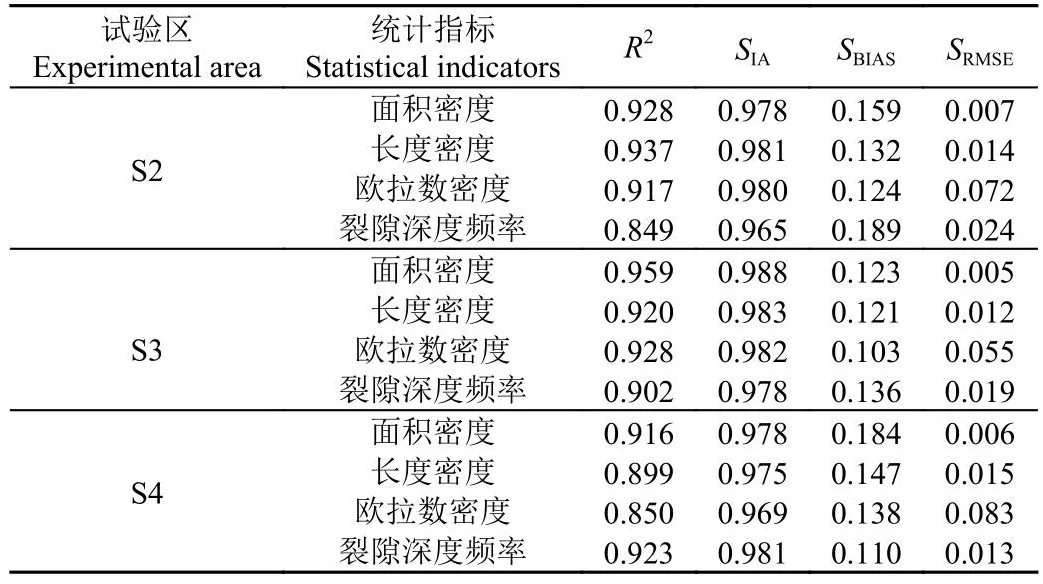
表5 模型验证结果评价指标Table 5 Evaluation indexes of model validation results

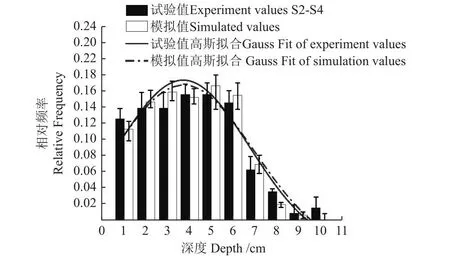
图10 试验与模拟裂隙深度频率分布比较Fig.10 Comparison between simulated and measured values of crack depth frequency

3.4 敏感性分析

因为纵向弹性系数Kz的变化代表不同性质（纵向弹性）土壤下裂隙形态以及裂隙深度分布的变化，所以本文在率定参数不变的前提下，选取土壤开裂结束时间（26 h），选择纵向弹性系数作为敏感性分析的参数，研究其变化对裂隙形态、裂隙深度频率以及Minkowski密度的影响。

图11 不同纵向弹性系数(KZ)下模拟裂隙沿土壤深度(h)的分层图像Fig.11 The layered image of simulated crack along soil depth (h)under different longitudinal elastic coefficient (Kz)

图12为裂隙发育结束后不同纵向弹簧系数Kz对裂隙深度频率分布的影响。结果表明，不同纵向弹性系数下，裂隙深度频率峰值不同，但变化形态基本一致。显然，随着纵向弹性系数的增大，在深度（h=1～4 cm）下，裂隙深度相对频率增大，这表明深度1～4 cm的裂隙占比越大。反之，在深度（h=5～10 cm）下，裂隙深度相对频率减小，这表明深度5～10 cm的裂隙占比越小。从整体上看，纵向弹性系数越小，裂隙沿深度方向发育的趋势越明显，深裂缝（h=5～10 cm）的占比越大。

图12 不同纵向弹性系数KZ下裂隙深度频率分布Fig.12 Frequency distribution of crack depth under different longitudinal elastic coefficient (Kz)

由Minkowski 密度函数定量描述不同纵向弹性系数下裂隙图像的变化（图13a和图13b），其面积、长度和欧拉数密度具有相同的变化规律，在同一深度，面积密度和长度密度随纵向弹性系数的增大而减小，表示裂隙数目随纵向弹性系数的增大而减小。其原因可能为土壤表面收缩相同的情况下，结构产生的总能量相同，纵向弹性系数的增大使得土壤结构弹性增强，导致下层节点位移减小，裂隙骨架的长度与宽度减小。

图13 不同纵向弹性系数（KZ）下的Minkowski函数Fig.13 Minkowski functions under different longitudinal elastic coefficient (KZ)

欧拉数反映的是裂隙网络连通性的指标，欧拉数密度函数的峰值随着纵向弹性系数的增大而减小（图13c），这表明孤立裂隙的数量是随着纵向弹性系数的增大在减小。正如图11所呈现的，纵向弹性系数越大，相同土层裂隙骨架的长度和宽度越小，孤立裂隙数越少。从而可以初步判断在相同的土壤深度下，由于纵向弹性系数的减小使得土壤结构弹性减小，增强了土体沿深度开裂的趋势。

4 结 论

本文基于Vogel模型引入了重力项，划分了三维弹簧网格，建立三维土壤干缩开裂模型，探究了纵向弹性系数对裂隙深度的影响规律。主要结论如下：

1）本文所建立的三维模型从土壤裂隙的表面动态形态特征和深度分布2个方面描述三维土壤裂隙。不仅较好地再现农田土壤表面干裂网络的动态形态特征，并且能够模拟土壤水分蒸发结束后的裂隙深度。应用Minkowski函数描述的农田土壤表面裂隙面积、长度、欧拉数密度随时间呈现增函数变化，符合自然裂隙的发育规律。面积、长度、欧拉数密度及裂隙深度频率的决定系数在0.849～0.959之间，一致性指标大于0.940，偏差在0.103～0.190之间，均方根误差在0.005～0.083之间，模拟结果较好。

2）纵向弹性系数越小，Minkowski密度函数峰值越大，同一深度下对应的土壤开裂程度越大，孤立裂隙数越多。纵向弹性系数的减小减弱了土壤弹性，使得下层两节点位移增大，深层土壤网格更容易因达到弹簧临界应变值而开裂，总体上促进了裂隙沿深度的发育。

本研究基于田间土壤试验区情况（土壤表面平整）建立了长方体弹簧网格结构，但未考虑复杂结构的情况，针对具有倾角的斜坡土壤可在后期构建不同类型网格结构进行研究。模型中以弹簧收缩描述水分蒸发引起的土壤收缩，但未考虑土壤含水率的变化。而现实中含水率变化的程度和速率会显著影响裂隙发育速率。在后续的研究中，可以尝试在三维模型的基础上耦合土壤的真实含水率，建立含水率与裂隙演化的关系，以提高模型的预测准确性及可靠性。此外，该模型未考虑复杂发育（弯曲、倾斜等）裂隙的情况，在未来需推广三维模型面对复杂裂隙情景下的应用。