联合Winkler-Pasternak模型的冬季输水梯形渠道冻胀力学分析

肖 旻 ，祝婉玲 ，王正中 ，吴 浪 ，杨晓松 ，崔 浩 ，葛建锐

（1.江西科技师范大学建筑工程学院，江西省科协智库防灾减灾工程技术研究基地，南昌 330013；2.西北农林科技大学旱区寒区水工程安全研究中心，旱区农业水土工程教育部重点实验室，杨凌 712100；3.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，兰州 730000；4.塔里木大学水利与建筑工程学院，阿拉尔 843300；5.兰州理工大学能源与动力工程学院，兰州 730050）

0 引 言

在中国北方广大旱寒地区，水资源短缺且时空分布不均的问题始终制约地区经济社会稳定、可持续发展[1]。为此，以渠道工程为主体的长距离跨流域调水工程、灌区更新改造工程及河湖连通工程将是未来国家大水网建设的重点[2]。然而冬季渠道极易发生冻胀破坏。对冬季停水渠道，众多学者对其冻害机理与力学模型等进行了研究[3-5]，但对冬季输水渠道的相关研究则相对较少。近年来，大中城市居民生活用水与工业用水量及其保证率大幅增加，对引调水工程常年输水、冬季输水的需求增大，冬季输水成为中国北方渠道运行常态[6-7]。对冬季输水渠道应给予更多关注。

对冬季停水渠道，冻胀力学分析的结构力学模型发展已较充分[2,8]。宋玲等[9]据此构建了冬季输水工况梯形渠道冻胀力学模型。但此类模型因没有考虑冻土与结构间相互作用，与实际工程存在一定偏差。弹性地基梁模型因其能够较好地描述冻土与结构间的相互作用，在各类冻土工程力学分析中得到推广应用[10-14]。就渠道而言，肖旻等[15]引入与衬砌板冻胀变形成比例的附加项反映冻胀力随衬砌变形的释放和衰减，构建考虑冻土-结构相互作用的梯形渠道Winkler冻土地基模型。李宗利等[16]类比土体沉降情形中的“基床系数”引入“冻胀力系数”的概念，基于Winkler理论建立梯形渠道冻土地基梁模型。何鹏飞等[17]将切向冻结力的影响引入力矩平衡构建控制方程，提出了考虑切向摩阻的梯形渠道弹性冻土地基梁模型。因为渠道衬砌为薄板结构且衬砌板弯曲程度通常不太大，文献[17]忽略了衬砌板自身弯曲对界面切向约束力的影响，即没有考虑法向与切向变形之间的耦合效应。JIANG等[18]参考赵明华等[19]对常温土弹性地基梁模型的研究对此进行修正，但需求解耦合方程组，计算过程繁琐。

长距离引调水工程往往需要跨越较大纬度，从而干渠将处于无冰输水、流冰输水以及冰盖输水等多种工况并存的复杂运行状态[20]。此外，通过水流控制、热力学控制等技术措施抑制或减少冰花的形成，促成冬季无冰盖输配水也具有广泛应用需求[21-22]。葛建锐等[6,23]在构造冰盖输水工况梯形渠道的Winkler冻土地基梁模型时，将冬季无冰盖输水作为特殊情形进行了探讨。Winkler模型计算简便且物理意义明确，但其忽略了土体连续性，即忽略土中剪力扩散，在非冻土中引起的误差通常较小。但对冻土而言，冰胶结作用使冻土的剪切系数普遍大于常温土，这必然影响模型精度[24-26]。因此，提出兼顾计算简便和模型精度的冻胀力学分析方法具有重要意义。

1 模型的建立与求解

1.1 基本假设

模型建立的基本思路：将冬季输水渠道基土分为冻结区与非冻结区。非冻结区采用Winkler模型构建法向冻胀变形控制方程，冻结区选用Pasternak双参数模型构建控制方程，两者共同构成冬季输水梯形渠道冻胀力学分析的Winkler-Pasternak模型。该模型同时兼顾Winkler模型计算简便、参数少、物理意义明确以及Pasternak模型考虑土体连续性从而精度较高的特点。最后通过对玛纳斯河流域某冬季输水梯形渠道的观测试验验证模型的合理性与适用性。结合已有研究及工程实践[2,3,8]，作如下假设：

1）由于渠内水的保温效应，冬季输水（无冰盖）梯形渠道分为冻结区和非冻结区两个部分，如图1。冻结区渠道基土等效为包含剪切层的Pasternak双参数地基[24-26]，非冻结区渠道基土等效为Winkler地基。

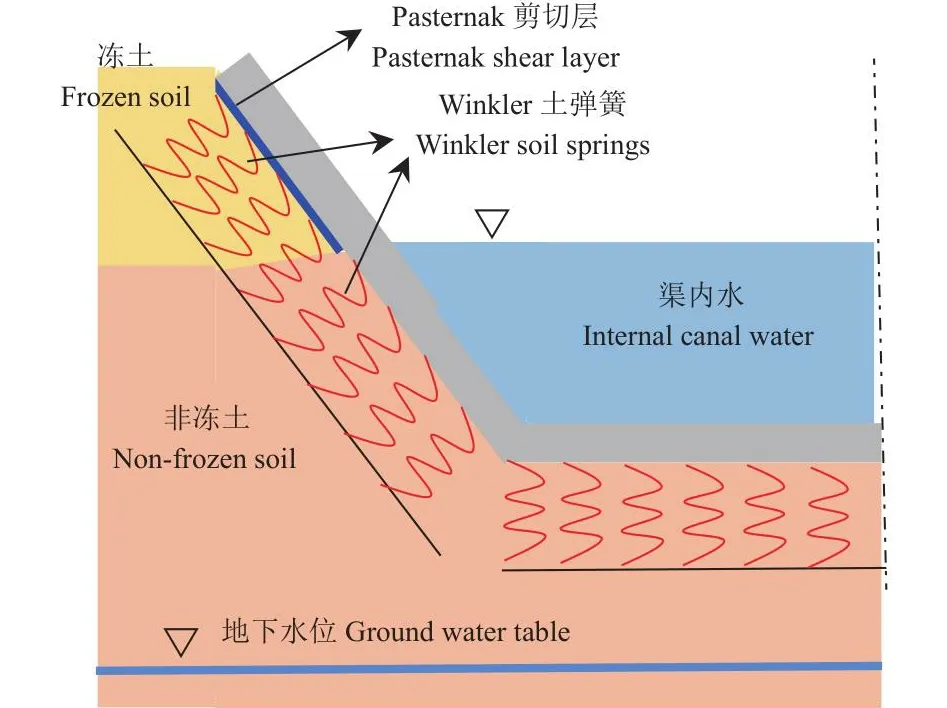
图1 冬季输水（无冰盖）梯形渠道断面示意图Fig.1 Section diagram of trapezoidal canal (without ice cover)with water delivery in winter

2）通过弹簧变形来反映冻土区土体的变形[2,16]。以基土自由冻胀量为弹簧原长，当受到约束无法达到原长时，由此引起的反力视为法向冻胀力；当冻土与衬砌间有脱开趋势时，弹簧伸长引起的反力视为法向冻结力。两者合称接触面法向应力。

3）渠道沿输水方向尺寸远大于横断面尺寸，力学分析可视为平面应变问题。冬季漫长，基土冻结速率缓慢，冻胀破坏过程视为准静态。未发生破坏时衬砌处于平衡状态，破坏时则处于极限平衡状态。

4）衬砌体为薄板结构且弯曲程度不太大，忽略其自身弯曲引起的切向反力对法向变形的影响[17,27]。

本文研究对象为现浇整体式混凝土衬砌梯形渠道。图2为渠道坡板冻胀力学分析简图。本文中下标为m时代表冻结区，为s时代表非冻结区，无下标则代表采用的是整体坐标系。A点为坡顶，B点为坡脚处，E点为冻结区与非冻结区的交界点即水位线。

图2 梯形渠道坡板受力情况Fig.2 Force situation of slope plate of trapezoidal canal

为方便叙述，冻结区采用局部坐标系om-xmym，以A点为原点，沿坡面向E点为x轴正方向，垂直坡面指向渠槽一侧为y轴正方向；非冻结区取局部坐标系os-xsys，以E点为原点，沿坡面指向B点为x轴正方向，垂直坡面指向基土一侧为y轴正方向。整体坐标系o-xy以A点为原点，沿坡面指向B点为x轴正方向，垂直坡面向渠槽一侧为y轴正方向。

1.2 冻结区控制微分方程

研究表明[2,8,18,28-29]，自由冻胀量u0(xm)为

式中u0(xm)为基土自由冻胀量，m；H为基土冻深，m；z(xm)为衬砌板各点地下水位，m；a、b为与当地气象、土质条件有关的经验系数，可由试验数据拟合获取。

各点自由冻胀量u0(xm)、衬砌板实际法向位移u(xm)及被约束的冻胀量uc(xm)有如下几何关系：

类比常温土Pasternak模型[24-26]，以图2所示微元体中的剪切层为分析对象，由静力平衡条件可得：q(xm)+dFQ/dx=q0(xm)=ko·uc(xm)，式中q(xm)表示作用在衬砌板底部实际的接触面法向应力，Pa；ko为冻胀力系数[2,16,27]，N/m3。

同时又有FQ=g·duc(xm)/dxm=-g·du(xm)/dxm（g为剪切层剪切系数，N/m），将该式代入前述静力平衡条件，即得作用在衬砌板上实际的接触面法向应力q(xm)为

式中[kou0(xm)]为当自由冻胀量被完全约束时作用在剪切层底部的法向冻胀力，视为初始冻胀荷载；[kou(xm)]则反映法向冻胀力随衬砌变形的释放和衰减效应，当冻土-衬砌间有脱开趋势时则转为法向冻结力；[gd2u(xm)/dxm

2]体现了剪切层挠曲引起剪力的扩散，并反映了土体连续性。参照文献[2,13-14,16,27,30]，冻土基床系数km为

式中km为冻土基床系数，N/m3；Ef为冻土的弹性模量，Pa；v为泊松比。基床系数指地表某处产生单位沉降位移需施加的单位面积上的外力；冻胀力系数指地表某处单位冻胀位移被约束引起单位面积上的约束反力。由此可见，两者之间具有一定相似性。鉴于此，结合文献[2,13-14,16,27,31-32]，可对式（4）作如下修正

式中ε为修正系数，按文献[2,16,27]取值。

再以图2所示微元体中衬砌板部分为分析对象，可导出Pasternak双参数地基梁的挠曲线微分方程，即冻结段各点法向变形的控制微分方程。如下式所示：

式中fm(xm)为初始冻胀荷载，Pa；βm、γ、ρ为特征系数；Ec为混凝土弹性模量，Pa；I为惯性矩，m4。应用Vlasov公式[27,33]计算剪切系数g，即g=(Ef·H)/[6(1+v)]。

1.3 非冻结区控制微分方程

对于非冻结段而言，采用局部坐标系os-xsys,则由Winkler弹性地基梁理论[24]，控制微分方程为

式中fs(xs)为渠内水作用在衬砌板的静水压力，Pa；βs为特征系数；γw为水体的重度，N/m3；θ为坡角，（°）；ko为非冻土基床系数[2,24]，N/m3。依Winkler假设，接触界面法向应力即地基反力q(xs)为

其中ko=0.65(1+v2)Es，Es为非冻土弹性模量，Pa。

1.4 控制微分方程的求解

联合应用式（6）、式（7）并考虑E点连续性条件及衬砌端部边界条件可得衬砌各点实际法向位移u(x)。

式（6）、式（7）均为4阶常系数非齐次线性方程，通解由齐次解和特解两部分组成。

使式（6）齐次化，则其特征方程为

式中rm为待定指数。式（9）的判别主要决定于ρ，根据取值不同可分为三种不同的情况[27]。以ρ＜1时为例（当ρ=1或ρ＞1时的情形可参见文献[27]），式（9）有两组共轭虚根，则式（6）有齐次解如下

式中φ1=βm(1+ρ)1/2，φ2=βm(1-ρ)1/2；cm1、cm2、cm3、cm4为任意常数。此外，式（6）还存在特解如下：

结合齐次解与特解，可得式（6）的通解为

使式（7）齐次化，则其特征方程为

式中rs为待定指数。由式（13）可得：

从而式（15）有如下4个根：βs(1±i)、βs(-1±i)。进而式（7）的齐次解u1(xs)为

式中cs1、cs2、cs3、cs4为任意常数。

式（7）还存在特解如下：

结合齐次解与特解，可得式（7）的通解为

通过以上分析可知，式（12）、式（17）共有8个任意常数需要确定。衬砌板两端须满足的边界条件为

式中ls为衬砌板非冻结区的长度，m；M为截面弯矩，N·m；Q为截面剪力，N。需要说明，冬季停水渠道的坡脚处因受渠道底板的约束而有u(xs=ls)=0。但对冬季输水渠道而言，在渠槽中水体重力的作用下该处应当发生沉降位移，即坡脚处位移实际上是远离底板的，故该处不再受到底板约束。

水位线即交界点E截面须满足连续性条件如下：

式中lm为渠道基土冻结区的长度，m。本文中冻结区与非冻结区对应衬砌板所选局部坐标系的纵坐标方向相反，故式（19）中等号的右侧出现负号。联立式（18）、式（19）即可得到8个任意常数，从而原方程得解。

1.5 计算流程

依据前述推导过程，可总结计算流程如下：

1）确定参数。参考文献[2,16,27,34]，冻胀力系数ko由常温土基床系数经修正后获取。确定自由冻胀量u0(xm)则需要首先确定参数a、b，条件允许时应当拟合野外观测或室内试验数据获取。针对参数a和b取值问题，众多学者对不同地区不同土质进行探究，目前已有丰富研究结果供参考和选用[2,8,29,35-37]。Pasternak剪切层剪切系数由Vlasov公式[27,33]获取。

2）依据式（1）可先确定冻结区基土自由冻胀量u0(xm)；再通过式（12）、式（17）可分别确定冻结区与非冻结区控制微分方程的通解u(xm)和u(xs)；基于此引入端部边界条件和截面E处连续性条件可确定任意常数cm1、cm2、cm3、cm4与cs1、cs2、cs3、cs4。作局部坐标系到整体坐标系的变换，则衬砌各截面挠度得解。

3）由式（3）、式（8）可分别计算衬砌板冻结区、非冻结区与渠基冻土间接触面法向应力q(xm)、q(xs)。在q(xm)、q(xs)以及静水压力fs(xs)共同作用下，依工程力学方法可计算各截面弯矩M(x)和剪力Q(x)。

注意到本文选取的整体坐标系y轴正方向朝上即指向渠槽一侧，各截面弯矩M(x)和剪力Q(x)为

4）为确保衬砌不会因冻胀而开裂，应对危险截面（即最大拉应力所在截面）作抗裂验算。计算式为

式中σ(xmax)为危险截面最大拉应力，Pa；d为衬砌板厚度，m；xmax为危险截面所在位置的坐标，m；N为截面轴力，N；[ε]为允许拉应变。

2 工程算例

2.1 工程概况

以新疆玛纳斯河流域某冬季输水梯形渠道为原型。该地区位于天山北麓，准噶尔盆地以南，渠灌事业发达，是著名的棉花和粮食产地。稳定冻结期日均气温约-12～-20 °C，属于温带大陆性气候。渠道坡板总长度l为3 m，冻结区长度lm为1.2 m，非冻结区长度ls为1.8 m，衬砌板厚度为0.1 m。渠基土质为壤土，参照文献[2,8,29,35]，参数a、b分别取21.97、2.20。混凝土弹性模量Ec为25.50 GPa，冻土弹性模量Ef为231.25 MPa，非冻土弹性模量Es为20 MPa。渠道基土冻深为1.1 m，渠道断面深度为2 m，地下水埋深（距渠顶）为3.5 m。因水下监测位移存在困难，加之衬砌板冻胀变形与破坏主要发生在水面以上的冻结区，故没有在水下设置测点。水面以上各测点通过布置监测装置（角钢、固定杆、固定架以及测杆等）并安装位移传感器（DN-15）观测衬砌变形，用水准仪补充观测和校正。

2.2 衬砌板法向位移与对比验证

结合边界条件以及截面E处连续性条件求解控制方程可得冻土区法向位移u(xm)及非冻土区法向位移u(xs)，统一到整体坐标系可得衬砌板法向位移分布。图3为本文模型即Winkler-Pasternak模型、Winkler模型、Pasternak模型计算值与实测值的对比图。

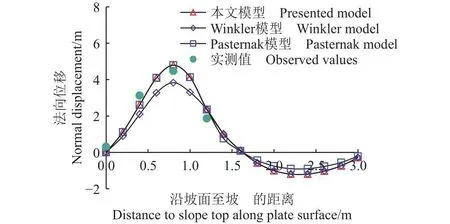
图3 坡板法向位移分布Fig.3 Distribution of normal displacement of slope plate

由图可知，本文模型、Winkler模型以及Pasternak模型计算结果均能较好地反映衬砌板法向冻胀/沉降位移的基本变化趋势。在水面以上冻结区衬砌板主要发生冻胀位移，在水面以下非冻结区则主要发生沉降位移，衬砌板冻胀-沉降过渡段大致处于水位线附近，这与工程实际相符。在冻结区，本文模型、Pasternak模型比Winkler模型的计算结果更接近实测值，表明由于冰胶结作用导致冻土剪切系数较大，从而冻结区应当采用考虑土体连续性的Pasternak模型更加准确、合理；因非冻结区基土剪切系数较小，Pasternak模型与Winkler模型计算结果差别不大，但Winkler模型比前者计算简便且所需参数少。由此可见，本文模型综合了两者的优点：在冻结区采用Pasternak模型，可以保证计算精度；在非冻结区则采用Winkler模型，计算结果在数值上相差不大，但保留了其计算简便、物理意义明确且所需参数少的特点。此外，与传统的冬季停水渠道不同，因渠内水静水压力作用，坡板在坡脚处（即距渠顶3 m处）应该是远离底板的，不再受底板约束，也使该处位移并不完全为零，存在一定的沉降位移，计算结果与理论预测相符。

2.3 截面弯矩分布与对比分析

局部截面弯矩过大是导致衬砌板鼓胀、隆起甚至开裂、折断的主要原因。因此，各截面弯矩的计算对衬砌板冻害分析至关重要。在获得衬砌法向位移分布后，依据式（20）可对各截面弯矩进行计算。对特定地区特定气候、土质条件下的具体渠道而言，地下水补给条件是决定基土冻胀强度，进而决定衬砌板截面内力和应力分布的主导因素。同时地下水埋深是衡量地下水补给强度的重要参数。为了进一步探索地下水埋深对各截面弯矩分布的影响规律，假定地下水埋深分别为2.5、3.5、4.5 m时计算各截面弯矩。

图4为不同地下水埋深时衬砌各截面弯矩分布图，以使衬砌凸向基土一侧为正。由图可见，冻胀力作用下冻结区衬砌板凸向渠槽一侧，渠内水静水压力作用下非冻结区衬砌板则主要发生沉降即凸向基土一侧，且因荷载方向发生改变而在衬砌板冻胀-沉降过渡段出现拐点，这与理论预测相符。衬砌各截面量值存在正负两个极值点，极值点附近量值较大同时其余部分量值较小，总体上冻胀段截面弯矩量值大于沉降段，截面弯矩最大值（绝对值）所在截面位于冻结区距离水位线约16.7%坡板长处。此外，随地下水埋深越大，冻胀段截面弯矩迅速减小，表明恰当地采用阻水排水措施降低地下水位或者减弱地下水补给，可有效减轻冻胀破坏风险[2-4,36]；沉降段截面弯矩则受地下水埋深的影响较小，这是因为该部分衬砌板沉降主要是由于渠内水静水压力导致，而静水压力不受地下水补给条件影响，这与实际相符。

图4 衬砌截面弯矩分布Fig.4 Distribution of section bending moment of lining

2.4 上表面应力分布

为了确定易开裂位置即危险截面并应用式（21）进行抗裂验算，有必要对衬砌各截面最大拉应力进行计算。在获得各截面弯矩分布后，由工程力学方法可对各截面最大拉应力进行计算。

考虑到衬砌板厚度通常较薄，弯曲变形也不太大，从而由于其自身弯曲而引起的接触面切向摩阻力较小，由此引起的截面轴力也较小，因此本文暂不考虑截面轴力对截面应力的影响。截面最大拉应力位于衬砌板上表面与下表面。前已述及，衬砌板冻胀段截面弯矩普遍大于沉降段，冻胀段截面弯矩较大而沉降段截面弯矩较小，且冻胀段上表面受拉，故仅以上表面应力为例。图5为渠道坡板上表面应力分布图。

图5 衬砌板上表面应力分布Fig.5 Distribution of upper surface stress of lining plate

由图可见，衬砌板冻胀段上表面产生拉伸变形，沉降段上表面则产生压缩变形。这是因为，冻胀力作用方向指向渠槽一侧，渠水压力作用方向则指向基土一侧。这将导致衬砌板冻胀段与沉降段各截面弯矩符号相反，从而在冻胀段凸向渠槽一侧使上表面产生拉伸变形，沉降段凸向基土一侧使上表面产生压缩变形。由图5还可以发现，上表面拉应力峰值大致位于冻结区距离水位线（即点E）10.0%~23.3%坡板长处，结合式（21）可知最大拉应变峰值也在此范围内，从而衬砌易开裂位置也在该范围内，这与工程实际基本相符。

3 讨 论

本文选取无冰盖输水的典型工况探讨了冬季输水梯形渠道冻胀力学分析方法。类似的方法同样能适用于冰盖输水情形。只需要参照文献[6,23,28]，同时考虑冻胀力-冰压力-渠内水静水压力联合作用，并把渠道基土划分为三个部分（即冻结段、过渡段和非冻结段），分别应用Winkler模型及Pasternak模型按段构造控制方程组，再结合端部边界条件及连接处的连续性条件即可求解。仍然存在的问题在于冰盖以下、水面以上的过渡段应该如何处理，有待后续进一步深入研究。

已有结构力学模型[9]假设法向冻胀力为均匀分布，未考虑冻结区各点因水分补给条件不同导致基土冻胀强度的差异，也未考虑冻土与衬砌间的相互作用，与工程实际存在偏差。现有Winkler模型[6,23]考虑了冻土与衬砌间的相互作用，但仍存在以下不足：在冻结区沿用不考虑土中剪力扩散的Winkler模型使计算结果产生偏差；在作用方向相反的冻胀力和静水压力共同影响下，冻结区衬砌板应以冻胀变形为主，非冻结区则主要发生沉降变形，且两者之间存在过渡区，已有模型无法体现该分布规律；因非冻结区主要发生沉降变形，因此渠道坡板在坡脚处实际不受底板约束，应设为自由边界，设为简支边界与实际不符。由此可见，区别对待冻结区与非冻结区，对冻结区应用Pasternak模型，对非冻结区仍采用Winkler模型，可联合两者的优点，克服已有模型的不足。

需要说明的是，由于法向冻胀变形是渠道抗冻胀设计的主要控制指标，本文主要讨论冻土-衬砌板之间法向相互作用，对接触面切向相互作用则没有涉及。此外，本文模型没有考虑冻土-结构间相互作用的空间变异性、非线性[38]等复杂特征，也未考虑脱开、架空等大位移情形。更全面、深入的模型有待进一步探索。

4 结 论

1）在已有研究基础上，考虑冻土与非冻土之间的差异，冻结区采用考虑土体连续性的Pasternak模型，非冻结区仍采用Winkler模型，结合两者优点并克服两者的缺点，提出联合Winkler-Pasternak模型的冬季输水梯形渠道冻胀力学分析方法。

2）以新疆玛纳斯河流域的某冬季输水梯形渠道为原型，分别采用本文模型即Winkler-Pasternak模型、Winkler模型、Pasternak模型对衬砌板法向冻胀沉降位移进行了计算。计算结果表明：三者的计算结果均能够较好地反映衬砌板法向位移基本变化趋势；依据法向位移渠坡衬砌板可划分为三个部分：冻胀段、沉降段、冻胀-沉降过渡段。相比其他两类模型，本文模型的计算值与实测值更加接近，表明模型的合理性。

3）对比分析表明，在冻结区本文模型计算结果比传统Winkler模型更准确，在非冻结区本文模型计算结果与Pasternak模型相比偏差很小，却保留了Winkler模型计算简便、物理意义明确、所需参数少等优点。对衬砌各截面最大拉应力的验算结果表明，易开裂位置在冻结区距水位线10.0%～23.3%坡板长处。