外包合同视角下的多设备分阶段成组维护策略
2023-08-08张馨予刘勤明叶春明谢世锐
张馨予 刘勤明 叶春明 谢世锐
上海理工大学管理学院,上海,200093
0 引言
近几年来,越来越多的工业企业将非核心但重要的设备维护业务外包给第三方机构以集中资源发展自己的核心业务。将生产线的设备维修工作委托给专业维修公司可在节省资金的同时获得更专业的服务[1]。多设备串联生产线较为常见,且单个设备故障造成的经济损失较大,因此研究串联生产线的维护外包策略问题十分重要。
维护外包的研究多以定性分析为主,如沈慧等[2]结合医疗设备的特点,构建关键指标体系来衡量维护外包商的服务质量。定量研究中,管理博弈方法居多,如ZHANG等[3]针对双渠道供应链,采用博弈论方法提出了制造商保修服务外包策略。少部分学者结合不同的背景对维护外包策略制定问题进行了定量研究,如ZHENG等[4]以保修期结束的风力涡轮机为研究对象,寻找能使维护服务成本最低的维修方案;CHAABANE等[5]以维修时间比较固定的飞机为研究对象,将内部维修和维护外包相结合,提出了一种以系统可靠度最大为目标的选择性维修策略。上述学者往往只考虑维护服务商的成本或设备维修的性能,对维护外包合同的特殊性以及第三方维修特点的考虑相对较少。
有学者从经济相关性、故障相关性[6]和结构相关性[7]等角度研究了多设备维护。从经济相关的角度来看,多设备维护分为机会维护[8-10]和成组维护,成组维护又包括直接成组[11]和间接成组[12-13]。杨元等[12]针对复杂系统构建了以系统维修成本最低为目标的间接成组维护模型。分阶段成组维护是间接成组维护的一种,相较于其他的多设备维护策略,具有易实践、维修效果好等特点,目前仅有少量学者对此进行了研究,且基本用于动车组相关设备或部件的维护,其中,文献[14-15]针对动车组相关设备,提出并深入探究了分阶段成组维护策略,即以牵引接触网为研究对象,以系统维护成本最小为目标,构建了分阶段成组维护模型,考虑了内外部冲击、动态订货、客流分布等不同因素对动车组分阶段成组维护的影响。综合来看,分阶段成组维护策略仅用于动车组相关设备维护的研究,该方法在常见机械设备维修中的实用性探究较缺乏,且现有研究对如何分阶段、如何成组的可实现性描述较为笼统、模糊,已有研究也并未将分阶段成组维护策略用于第三方维护外包领域。
综上,将多设备维护服务外包给第三方机构可为企业节约人力、资金和机会成本,但是只有用科学的方法合理约束、有效激励维护外包商,才能获得更优质的维修服务,保证生产线的高效运行。本文将兼具经济性和实用性的分阶段成组维护策略应用到多设备串联生产线的维护外包决策。首先,将设备使用者对维护外包服务质量的感知融入到维修合同定价策略,采用不同的合同定价方式激励第三方做到更好。然后以可靠度为约束构建维护外包商利润模型,通过对比分阶段成组维护和传统成组维护策略来验证模型的有效性和实用性。
1 问题描述及假设
本文以生产制造企业第三方维护外包为研究背景,以多设备串联生产系统为研究对象,以分阶段成组维护为主要的维护策略,考虑企业对第三方维护服务的满意度,构建不同满意度之下的分段式维护服务商利润模型。在各设备可靠度约束下,维护外包商可以通过智能优化算法得出不同分阶段策略下使利润最高的基础预防性维护间隔ΔTs(s=1,2,…,S)、基础预防性维护次数ns、设备i所属的最优组别pi和最合适的平均故障响应时间y,再通过对比得出最佳的分段方案和成组维护策略,以制定出合同周期内生产系统的维护计划。
为使模型构建更为合理,提出如下假设:①维护外包的类型为选择性外包,主要维护策略为分阶段成组维护和故障后小修;②签订维护外包合同时,设备均为全新,即初始役龄为0;③各设备负责产品生产中的不同工序,设备之间相互独立。
2 模型构建
2.1 多设备分阶段成组维护模型
传统的间接成组维护是在一定维护区间内确定基础维护间隔ΔT,并将系统中的所有设备分为P组,其中,第p(p=1,2,…,P)组设备的维护间隔设置为基础维护间隔的整数倍即pΔT。这种维护方式将多设备系统的维护任务按照时间轴有规律地集中在一起,以减少共同的维护成本(人力资源成本、维修工具成本等)。
分阶段成组维护在传统间接成组维护的基础上,将基础维护间隔依据实际情况进行分段,不同阶段对应不同的基础维护间隔,并缩短基础维护间隔。如图1所示,将维护外包合同周期L分为S阶段,阶段s对应的基础维护间隔为ΔTs,即第一阶段的基础预防性维护间隔为ΔT1,基础预防性维护次数为n1;第二阶段的基础维护间隔为ΔT2,基础维护次数为n2;…;第S阶段的基础维护间隔为ΔTS,基础维护次数为nS,其中,ΔT1>ΔT2>…>ΔTS。与传统的间接成组维护类似,分组后第一组设备的预防性维护间隔为分段后的基础维护间隔,第p组设备的维护间隔为p个基础维护间隔。

图1 分阶段成组维护示意图
据此可得串联系统的基础维护间隔。第一阶段进行n1次预防性维护,对应的基础预防性维护间隔均为ΔT1;以此类推,第S阶段的nS次预防性维护对应的基础维护间隔均为ΔTS。则合同周期内,第j次预防性维护对应的基础维护间隔为
(1)
第一组设备的预防性维护间隔为基础维护间隔,总预防性维护次数为各阶段的基础维护次数之和,结合式(1)可得第一组设备中的设备i的第j次预防性维护间隔Ti,j,1和总预防性维护次数Ni,1:
Ti,j,1=Tj,0
(2)
(3)
第二组设备中设备i的第j次预防性维护间隔Ti,j,2及该设备的总预防性维护次数Ni,2:
(4)

(5)

同理可得,第p组设备中的设备i的第j次维护间隔Ti,j,p及总维护次数Ni,p:
(6)

(7)
2.2 串联生产系统的故障分布及可靠度模型
串联生产系统共有m个设备,设备i(i=1,2,…,m)的故障率均服从形状参数θi、尺度参数ωi的Weibull分布,则部件i的故障率分布函数为
(8)
设备i经过一次预防性维护后,性能都会有一定程度的改善,但是随着维护次数的增加,改善效果会逐渐下降,故引入动态役龄递减因子ηi(j)来描述设备i在第j次预防性维护后的役龄回退量[16]:
(9)
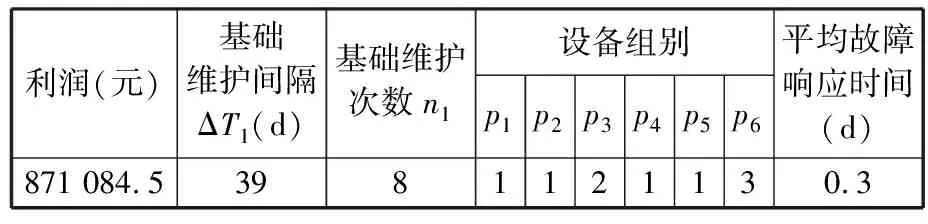
式中,Ci,pm、Ci,rm分别为设备i的预防性维护成本和更换成本;ai为设备i的成本调整参数,0 (10) 由此推导可以得出设备i在第j(j=2,3,…)次预防性维护前后的有效役龄: (11) (12) 通过役龄递减因子的修正,得出设备i在第j+1个预防性维护周期内的故障率: (13) t∈(0,Ti,j+1,p) 部分设备在经过Ni,p次预防性维护后,距离维护合同总周期L的时长α小于最后一次维护的间隔,因此不会进行下次维护,但在该间隔仍可能产生故障,故该设备在整个维护外包合同周期内的总故障次数为 (14) 单个设备的可靠度与故障率关系式为 (15) 每次预防性维护后,故障率都会有所下降,因此可以通过分段累加求得设备i在合同周期L时刻的可靠度: (16) 维护服务需求方根据生产系统可用度和平均故障响应时间设定满意度函数,通过满意度的高低对维护合同价格进行分段。如果维护使生产系统的使用度较高,维护外包服务商在故障发生时的响应也比较及时,则维护服务需求方的满意度高,愿意提供更高的合同价格来激励外包商。 本文中,生产系统的可用度[17]是指合同总周期减去维修导致的停机时间后的剩余时间与总合同周期的比值: (17) 式中,Tpm为单次预防性维修所需时间;Ti,cm为设备i进行故障后小修所需时间。 生产系统的可用度越高,维护服务需求方的满意度越高。维护服务需求方的满意度为 (18) 式中,Amin为最低可用度;γ为可用度满意度的形状参数。 时间满意度函数[18-19]通常用于物流选址和调度问题,表示企业对客户服务响应快慢的满意程度。本文结合第三方维护的特殊性,将其引入维护外包合同的定价。生产系统中的某个设备发生故障时,需要维护外包商快速维护,但快速响应会提高维护外包商的成本,因此求出最优的平均故障响应时间来为维护外包商的故障响应提供决策依据。维护服务需求方的满意度为 (19) 式中,ymax为维护服务需求方可以接受的最长时间;ymin为维护服务需求方最理想的故障响应时长;ξ为该满意度函数的形状参数。 结合式(19)、式(20)得出最终的满意度函数: D=DADy (20) 维护服务承包商的收益函数为 (21) 式中,D为维护服务需求方的满意度;Dmin为不可接受的满意度;D1为维护外包商获得线性激励报酬的满意度临界值;Q1为基础报酬金额;β为收益激励系数。 维护外包商在维护合同周期内需要承担的费用主要包括预防性维修总成本Cpm、故障后小修总成本Ccm和发生故障时维护外包商响应延迟的惩罚成本Crp,则合同周期内的总费用为 C=Cpm+Ccm+Crp (22) (1)预防性维修总成本。预防性维护成本是由串联生产系统中所有设备每次预防性维护的成本Ci,pm和分阶段成组之后多个设备在同一时间进行维护的可共用成本Cgm之和,因此预防性维护的总成本为 (23) (2)故障后的小修总成本。某个设备突然发生故障时维护外包商会对其进行小修。合同周期内,整个生产系统的故障小修总成本由所有设备每次小修的单次成本Ci,cm加总得出: (24) (3)故障响应延迟的惩罚成本。对于串联生产系统而言,任意一个设备发生故障都会导致生产停滞,产生高额的生产损失。因此在维护合同签订前,维护服务需求方会对第三方维护外包商的响应速度提出预期要求。如果合同周期内设备的平均故障响应时间大于维护服务需求方的预期要求时间t0,则会对维护外包商进行惩罚,要求其缴纳一定的赔偿,且平均故障响应时间越长,需要做的赔偿越多,则维护外包商需要承担的故障响应延迟惩罚成本为 Crp=Crp0max{0,y-t0} (25) 式中,Crp0为延时惩罚成本。 维护外包商的利润为收益与成本的差值: π(ΔTs,ns,pi,y)=Q(ΔTs,ns,pi,y)-C= (26) 仅以维护外包商利润最大为目标而不加以约束,则可能出现维护方案经济效益高而设备性能保持不足的问题,因此本文在求解最优目标时,将生产系统中各设备的可靠度作为主要的约束条件,即设备i在合同周期L时刻的可靠度Ri(L)均需大于既定的最低可靠度限制R0。由此得出最终的单目标决策模型: (27) 麻雀算法[20]是模拟麻雀的觅食过程而提出的一种求解最优目标的群优化算法,该算法对变量的搜索能力较强,应用场景广泛。本文采用的多策略融合麻雀搜索算法[21]是针对麻雀算法容易陷入局部最优、收敛较慢等问题提出的改进算法,主要改进点为引入鸡群算法中的随机跟随策略来优化麻雀加入者的位置更新,应用柯西-高斯变异来优化迭代过程中的全局最优解等。 多设备分阶段成组维护模型以维护服务外包商利润为目标函数,以各设备的可靠度为主要约束,以各设备所属组别、基础维护间隔、基础维护次数为整数决策变量,以平均故障响应时间为连续决策变量,因此该问题属于有约束的多类型变量单目标优化问题。针对约束,采用罚函数[22]对算法进行改进;为使各设备所属组别、基础维护次数等整数决策变量的值在算法迭代过程中恒为整数,在求解每个个体的适应度函数时将其向下取整。 3.1.1初始化种群 首先确定分阶段成组维护策略对应的阶段数S,然后将随机生成q组S阶段成组维护对应的决策变量作为q个麻雀个体的位置坐标,并对生成的每个个体进行约束判断,如果不满足条件则重新生成,最终得到均满足约束的初始种群: (28) ΔTs,k=(ΔT1,k,ΔT2,k,…,ΔTS,k) ns,k=(n1,k,n2,k,…,nS,k) pi,k=(p1,k,p2,k,…,pm,k) 式中,ΔTs,k为第k个麻雀个体的基础维护间隔,k=1,2,…,q;ns,k为第k个麻雀个体的基础维护次数;pi,k为第k个麻雀个体对应的m个设备各自所属组别。 3.1.2计算适应度函数 每只麻雀所在位置的食物多少由适应度函数来表示。本文在计算适应度函数时,引入罚函数对主要约束条件进行处理,以加快算法的收敛。处理后的适应度函数为 Fk(ΔTs,ns,pi,y,σ)=πk(ΔTs,ns,pi,y)+ (29) 式中,γ为惩罚因子;gk,i(ΔTs,ns,pi,y)为第i个约束条件。 3.1.3发现者位置更新 选取种群中70%的个体为发现者,判断每个发现者个体的预警值和和安全值的关系,如果预警值Ea小于安全值fa,则采用搜索范围较大的更新公式更新个体;如果预警值Ea大于等于安全值fa,则通过计算将个体位置移送到安全区域。具体的位置更新公式如下: (30) 其中,g为当前的迭代次数;Xij(g)为第g次迭代第i个麻雀个体的第j维变量;τ为0~1内的随机数;φ1为满足正态分布的随机数;W为1×D维的矩阵,且元素均为1;Imax为最大迭代次数。 3.1.4加入者位置更新 种群中除发现者外剩余30%的个体即为加入者(个体数量为q1)。传统麻雀算法中,i≤q1/2时,加入者个体会直接向局部最优个体的位置靠拢,而鸡群算法的随机跟随策略是让个体按照一定的概率向最优位置收敛,在保证收敛性的同时提高了种群多样性。因此采用鸡群算法的随机跟随策略对其进行优化后的加入者个体位置更新,具体公式如下: Xij(g+1)= (31) S1=exp(Fk-Fi)k∈[1,i)∪(i,q] 式中,Xworst(g)为第g次迭代中适应度值最差的麻雀所在位置。 3.1.5危险者更新 设定种群中的警戒者为种群中随机选取的20%个体,按照传统麻雀算法的危险者更新公式 Xi,j(g+1)= (32) 计算更新这部分麻雀个体的位置。其中,φ2为步长控制参数,是一个服从正态分布的随机数;v为麻雀方向调整参数,是一个服从[-1,1]均匀分布的随机数;ε为极小值,用于防止分母为0的情况发生;Fbest、Fworst分别为当前迭代中最优和最差的适应度函数值。 3.1.6柯西-高斯变异 针对麻雀算法迭代后期个体位置加速同化、易陷入局部最优的问题,引入柯西-高斯变异策略对当前最优个体位置Xbest(g)进行变异,经过了柯西高斯变异的位置坐标为 (33) 其中,δ1为服从柯西分布的随机变量,即δ1~C(0,σ2);δ2为服从高斯分布的随机变量,即δ2~G(0,σ2)。柯西高斯变异的标准差为 (34) 综上,绘制出算法流程图(图2),算法的具体步骤如下: 图2 算法流程图 (1)确定算法的相关参数。 (2)初始化麻雀种群,获得满足约束的初始麻雀种群。 (3)计算适应度函数,进行适应度排序和种群排序。计算初始麻雀种群中每个个体的适应度,对个体适应度按从小到大依次排序,再将种群中个体的位置与排序后的适应度一一对应。通过索引取出第一个麻雀的位置,并将其暂时储存为全局最优位置,对应的适应度则为最优适应度。 (4)按照式(31)对麻雀种群中的发现者进行位置更新。 (5)按照式(32)对麻雀种群中的加入者进行位置更新。 (6)从种群中随机选取部分个体作为警戒者,并对这部分个体进行位置更新。 (7)柯西-高斯变异。重复步骤(3),对最终更新后的种群进行适应度排序和种群排序,之后取出最优个体进行柯西-高斯变异。将变异后的个体与原最优个体的适应度进行比较,如果变异后的个体适应度更大,则更新全局最优个体的位置和适应度。 (8)重复步骤(4)~(7),直至迭代结束。输出全局最优解及其对应的适应度。全局最优解为所求的最优维护方案,对应的适应度为该方案维护外包商的最大利润。 本文以某制造企业需要维护外包的驱动器关键零部件生产线为研究对象,通过算例分析来验证模型的实用性。该生产线由6台机械设备组成,主要包括注塑工艺相关设备和喷涂工艺相关设备,如图3所示。对设备进行编号,其中,注塑上料机为设备1,注塑加工机为设备2,注塑件分拣机为设备3,喷涂上料机为设备4,喷涂机为设备5,喷涂件分拣机为设备6。为描述方便,生产线中所有设备在下文均以设备编号的形式出现。 图3 驱动器关键零部件生产线示意图 参照现实中的外包场景,确定维护外包合同的总签订周期为1年即L=365 d。维护外包合同规定不可接受满意度Dmin=0.5,固定报酬Q1=200 000元;线性激励满意度阈值D1=0.65,收益激励系数β=2 400 000。参考相关文献,并结合企业生产实际确定满意度相关参数,其中,不可接受可用度Amin=0.8,可用度满意度的形状参数δ=0.5;故障响应时间满意度函数中,理想故障响应时间ymin=0;维护服务需求方不可接受的响应时间ymax=3 d,故障响应时间满意度的形状参数ξ=0.5。 合同周期内,每个设备的可靠度必须大于0.7。通过采集该生产线上各设备的实际运行数据,确定最终的设备维护相关参数取值,如表1所示。 表1 设备维护相关参数 考虑到维护外包商参照维修计划进行维护时的便利性和可操作性,以及维护策略制定的难易度,本文以两阶段、三阶段和四阶段的成组维护为主要探讨对象,通过优化算法求解能使企业满意度更高、维护外包商利润最大的维护方式,并给出不同分段策略对应的维修计划。 4.2.1两阶段成组维护结果 首先,用多策略融合的麻雀搜索算法求解两阶段成组维护模型,其中,种群个数设置为200,最大迭代次数设为150,应用python对该模型进行求解所得的最优结果如表2所示。 表2 两阶段成组维护的最优结果 6个设备的最优分组策略如下:设备1、2、4、5为第一组;设备6为第二组;设备3为第三组。第一组设备的预防性维护间隔为基础维护间隔,即第一阶段的维护间隔为58 d,维护次数为4;第二阶段的维护间隔为37 d,维护次数为3。第二组设备在整个外包合同周期内以116 d的间隔维修2次,以74 d的维修间隔维修1次。第三组设备在外包合同周期内以174 d的维修间隔维修1次,以132 d的维修间隔维修1次。计算得出的最优平均故障响应时间为0.3 d,因此在维护合同周期内,如果有设备发生故障,维护外包商可以以最优响应时间0.3 d为标准为工厂提供故障小修服务。 结合该方案可以制定出图4所示的维修计划。在整个维护外包合同周期内,维护外包商共计需要进行7次预防性维护。第一组(设备1、2、4、5)在外包合同周期内维修7次,在第2、4、6次维护时维护第二组(设备6),在第3、6次维护时维修第三组(设备3),以减小整条生产线的总维修次数。该方案对应的最大利润为882 276.6元。 图4 两阶段成组维修计划示意图 4.2.2三阶段成组维护结果 用同样的算法对三阶段成组维护模型进行求解。与两阶段成组维护求解相同,种群个数设置为200,最大迭代次数设置为150,应用python对该模型进行求解所得的最优结果如表3所示。 表3 三阶段成组维护的最优结果 三阶段成组维护对应的设备最优分组策略如下:设备2、4、5为第一组;设备1、3为第二组;设备6为第三组。第一组设备的维修间隔为基础维护间隔,即在第一阶段以36 d的间隔维护3次;第二阶段以31 d的间隔维护3次;第三阶段以24 d的间隔维护5次。在合同周期内,第二组设备首先以72 d的维护间隔维修1次,再以67 d的维修间隔维修1次,第三次维修间隔为62 d,最后再以48 d的间隔维修2次。第三组设备的第一次维修间隔为108 d,第二次维修间隔为93 d,第三次维修的间隔为72 d。平均故障响应时间仍为0.3 d。 若维护外包商选择三阶段成组维护策略,则可按照图5所示的计划进行维修。第一组(设备2、4、5)在外包合同周期内维修11次,在第2、4、6、8、10次维修时维修第二组(设备1、3),在第3、6、9次维修时维修第三组(设备6)。该方案对应的最大利润为906 777.6元。 图5 三阶段成组维修计划示意图 4.2.3四阶段成组维护结果 用同一算法求解四阶段成组维护策略的最优方案,其中,麻雀种群数量设置为200,最大迭代次数设置为150。用python求解该模型,所得最优方案如表4所示。 表4 四阶段成组维护的最优结果 四阶段成组维护对应的设备最优分组策略如下:设备2、4、5为第一组;设备3、6为第二组;设备1为第三组。第一组设备以基础维护间隔和基础维护次数进行维修,即第一阶段的基础维护间隔为33 d,维修次数为2;第二阶段的基础维护间隔为28 d,维护次数为2;第三、第四阶段的基础维护间隔分别为25 d和20 d,基础维护次数均为4。在外包合同周期内,第二组设备总计维护6次:第一次维护间隔为66 d,第二次维护间隔为56 d,第三、第四次维护间隔为50 d,第五、第六次维护间隔为40 d。第三组设备的第一次维护间隔为94 d,第二次维护间隔为78 d,第三次维护间隔为70 d,第四次维护间隔为60 d。平均故障响应时间为0.2 d,维护外包商在设备发生故障时的最优响应时间为0.2 d。 如果选择四阶段成组维护策略,则可以按照图6所示的计划进行维修:第一组(设备2、4、5)在合同周期内维护12次,第2、4、6、8、10、12次维修时维修第二组(设备3、6),第3、6、9、12次维修时维修第三组(设备1)。与两阶段、三阶段相比,四阶段成组维护策略所得利润最大,为979 091.7元。 图6 四阶段成组维修计划示意图 整个维护外包周期内,传统成组维护的基础维护间隔为ΔT(恒定值)。分阶段成组维护是一种优化的维护策略,考虑了设备在使用后期故障率加速递增、更易出现故障的状况,将维护外包周期分阶段并使基础维护间隔随着阶段数的增加而缩短。 为比较分阶段成组维护和传统成组维护,本文采用相同算法求得传统成组维护的最优结果,如表5所示。传统成组维护的基础维护间隔都为39 d,最优的基础维护次数为8。6个设备的最优分组策略如下:设备1、2、4、5为第一组,设备3为第2组,设备6为第三组。维护外包商的最优平均故障响应时间为0.3 d。该方案对应的利润为871 084.4元。 表5 传统成组维护的最优结果 4种分组维护策略的最大利润及各设备的可靠度如表6所示。与分阶段成组维护相比,传统成组维护的利润较低,除设备1的可靠度高于分阶段成组维护外,其余设备的可靠度均低于三、四阶段成组维护的可靠度。 表6 不同分组维护策略对应的目标值及约束值 对比分阶段成组维护的最大利润和可靠度,可得四阶段成组维护的利润最高;相较于三阶段成组维护,四阶段成组维护在保证多数设备可靠度更高的前提下,使利润提高了7.95%,在提高经济效益的同时也保证了维修质量。 与两阶段成组维护相比,三阶段成组维护的利润明显较高;设备2、3、4的可靠度增加值大于0.04,设备6的可靠度增加值大于0.01。 综合来看,四阶段成组维护策略的质量最高,在保证各个设备高可靠度的情况下,让维护外包商获得最大利润。因此,维护外包商可以在维护合同周期内将四阶段成组维护作为主要的维护策略,参考该种维护策略对应的维修计划对该生产系统进行维护。 本文针对生产实际中常见的多设备串联生产系统维护外包场景,构建了基于维护服务需求方满意度的合同定价模型及第三方维护外包服务商利润模型。维护合同确定的维护策略为传统成组维护与单设备分阶段维护相结合的分阶段成组维护策略。通过多策略融合的麻雀搜索算法,求出不同分组维护策略的基础维修间隔、基础维护次数、各设备的最优分组、维护服务商的最佳平均故障响应时间,并据此得出对应的维修计划。通过分析算例结果可以得出四阶段成组维护在保证各设备高可靠度的同时,让维护外包服务商获得更多利润,验证了四阶段成组维护策略在普通机械设备组成的生产线维护外包中的实用性和优越性。 合同双方签订维护外包合同时,可以参考分段式合同定价激励维护外包商提高维护服务质量,给予维护需求方更佳的维护外包服务体验。同时,企业和维护外包商也可采用类似的流程得出最优的四阶段成组维护方案,据此制定合同周期内的预防性维护计划,并参照最优的平均故障响应时间提供故障小修服务。本文提出的维护外包模型已应用于某制造企业的驱动器关键零部件生产线相关设备维护,与传统的维护模式相比,分阶段成组维护策略具有明显的优势。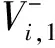

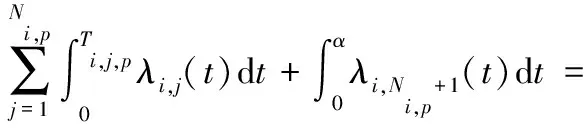



2.3 合同定价模型
2.4 合同周期内总成本模型
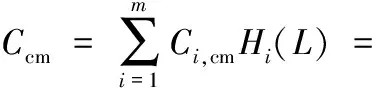
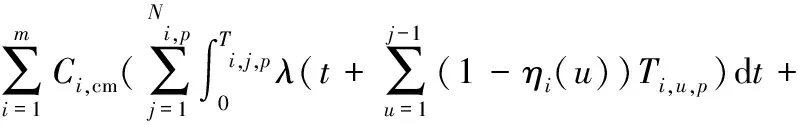

2.5 维护服务外包商利润模型
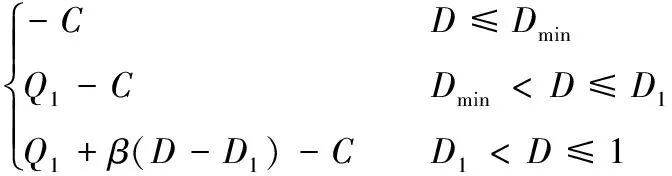
2.6 单目标决策模型
3 模型求解
3.1 算法设计
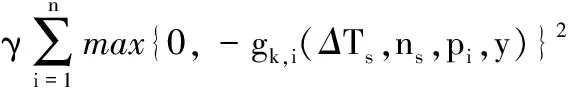
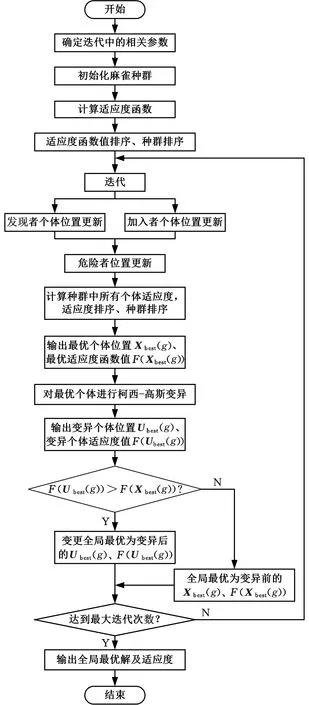
3.2 算法步骤
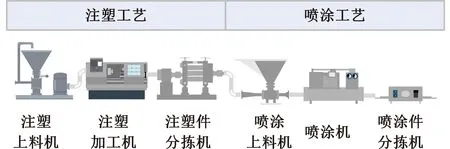
4 算例分析
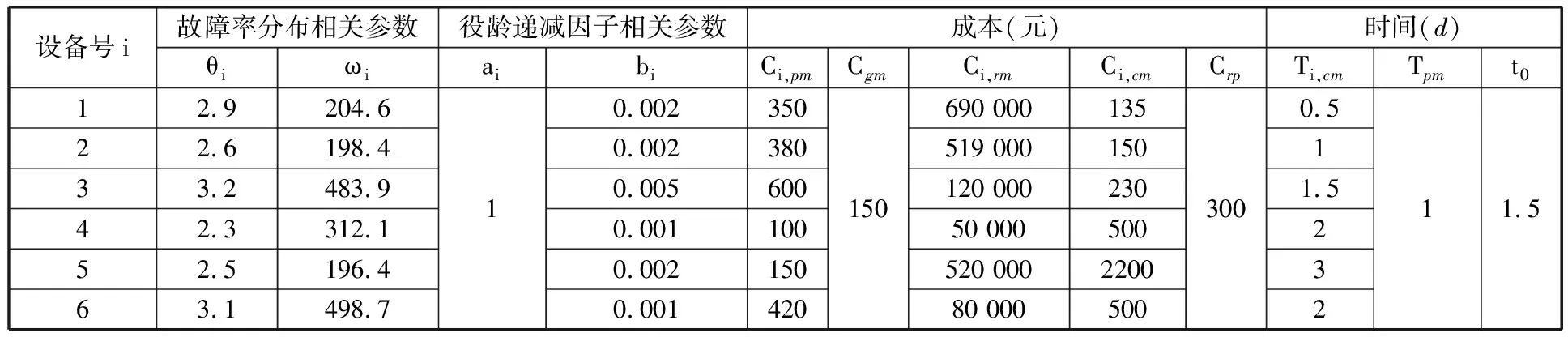
4.1 数据准备
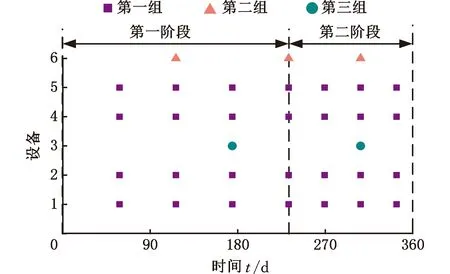
4.2 结果分析


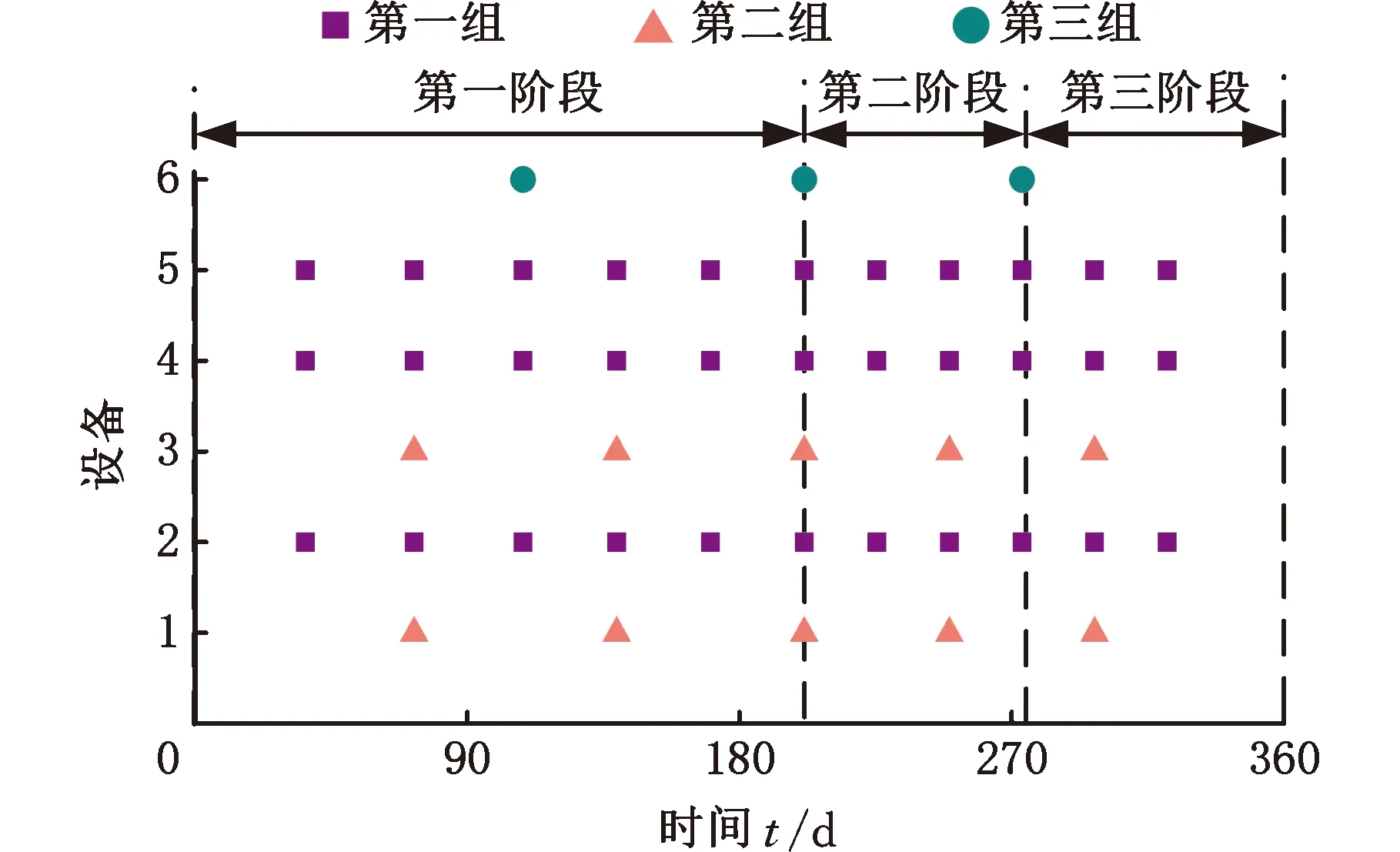

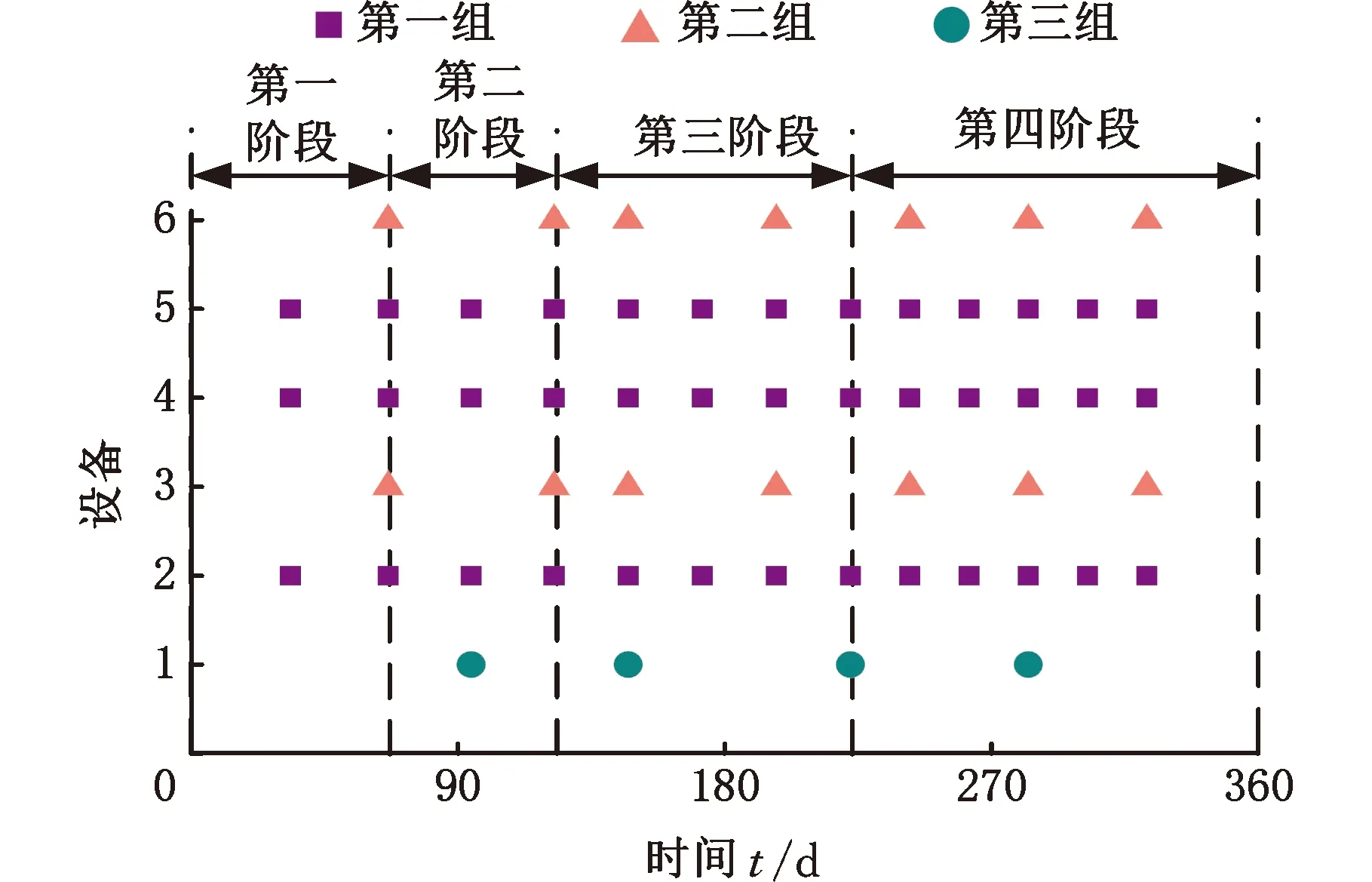
4.3 结果比较

5 结论
