需求扰动作用下的供应链库存系统优化模型
2023-08-08吴迎年李庆奎
吴迎年 张 晶 李庆奎 焦 帅
1.北京信息科技大学自动化学院,北京,1001922.智能物联与协同控制研究所,北京,100192 3.高端装备智能感知与控制北京市国际科技合作基地,北京,100192
0 引言
供应链系统是由生产商、经销商、零售商等环节组成的复杂网络系统。供应链系统中,库存系统是企业生产运营的重要组成部分,直接影响供应链系统能否正常运转,因此库存系统的管理与优化成为供应链管理领域的重要研究方向[1-4]。相对于单个企业的库存系统而言,完整的供应链库存系统由上下游多个环节的库存系统组成。供应链的上下游企业相互影响,提高了供应链库存系统的管理难度。现代供应链体系中,库存系统面临的挑战源于多个方面[5-7]。市场需求具有复杂、变化周期长、突变性强等特点,这使得管理者意识到传统的供应链库存管理方式已经不足以应对现代复杂的市场环境。因此,提高供应链库存系统的鲁棒性和抗扰动能力,实现对供应链库存系统的有效控制,是避免供应链上下游企业巨大经济损失的重要手段。
现代供应链库存系统面临的挑战越来越复杂,许多企业管理者和科研人员对需求不确定的供应链库存系统优化管理进行了大量的研究[8]。从研究方法看,这些研究主要分为三大类:①以数理统计分析为基础,根据企业目标需求构建多目标优化不等式,利用数学分析法进行分析求解,帮助企业制定合理的库存管理策略[9-12]。此类方法虽然能得到较为准确的理论结果,但在构建多目标优化不等式的过程中会设置过多的假设。②采用数字孪生技术等计算机仿真方法分析供应链库存系统的动态过程[13-15]。此类方法要求较高,虽然能获得供应链库存系统准确的运行状态,但需对供应链库存系统进行细节建模,工作量较大,工程难度较高。③以离散理论为基础,从控制角度出发将供应链库存系统看成被控对象,将企业需求看成控制目标,选择合适的控制方法进行有效控制,帮助企业制定科学合理的运营策略[16-18]。此类研究方法从控制角度给出清晰、严谨、科学合理的库存管理方法,设置的假设较第一类方法少,供应链库存系统模型的构建比较简单。
由于自动化控制理论的发展及其在需求未知情况下的优化管理供应链库存系统的独特优势,越来越多的学者利用控制思想来解决需求不确定性的供应链库存系统管理问题。利用控制思想解决此类问题时,可将需求不确定量看成需求扰动。POLOTSKI等[19]利用自适应控制设计了易故障制造系统的控制器,实现生产和库存的优化管理。赵川等[20]基于自抗扰控制,设计了随机扰动作用下的供应链库存系统优化模型,减小了扰动对库存系统的影响。BARTOSZEWICZ等[21]基于滑模控制的思想对储存量受限的生产商进行优化管理,以实现不同需求下的生产管理。上述研究以现代控制理论和状态空间算法为指导,解决了需求扰动下的供应链库存系统优化问题,但仅仅考虑了对供应链系统单一环节的优化控制,缺乏对扰动作用下的完整供应链库存系统的优化。徐君群[22]从鲁棒 H∞控制角度出发,研究了外部需求不确定的动态闭环供应链网络的总成本问题。FU等[23]基于分布式模型预测控制,寻求供应链系统交互节点的输入/输出约束及交叉耦合问题的最优解决方案,帮助供应链系统以最低的库存成本满足外部的不确定需求。上述研究从完整供应链系统的角度出发,解决了扰动作用下的库存系统管理优化问题,但仅考虑了外部需求扰动对供应链系统的影响,忽略了多环节供应链库存系统信息不对称引起的内部潜在需求扰动。
滑模控制(sliding mode control,SMC)主要包括两个方面的内容:构造合适的滑模面,选择合适的趋近律。滑模控制因算法简单、抗扰动性强等特点[24]而被广泛应用于工程控制领域[25-27]。传统的滑模控制存在抖动性强的缺点[28],这会进一步加大库存波动,增加库存运营成本,极大限制了传统滑模控制在库存管理领域的应用。
针对传统滑模控制的不足,本文提出一种基于自适应指数趋近律的改进型滑模控制。在指数趋近律的基础上设计一种自适应的变指数趋近律,即根据控制状态自适应调节控制趋近律,并对符号函数sgns进行平滑处理,有效解决了传统滑模控制抖动性强的问题,使其适用于库存管理。为解决需求扰动作用下完整供应链库存系统的优化管理问题,设计了一种基于改进型滑模控制器和扰动观测器相结合的供应链库存系统优化模型,其中,改进型滑模控制器在控制供应链系统各环节的库存量快速趋于企业目标库存量的同时削弱内部潜在需求扰动的影响。利用扰动观测器实时测量跟踪可测量的外部需求扰动,并通过前馈补偿控制主动消除外部需求扰动对供应链库存系统的影响。
1 构建三级网状供应链库存系统动态模型
本文对包含生产商、经销商、零售商的三级网状营销模式进行建模与分析。三级网状供应链系统营销模式见图1,图中,箭头线表示产品的销售路线。一个生产商向不同区域的多个经销商发货,经销商再以一对多或一对一的形式将产品分发给零售商,零售商在不同的销售区域销售产品。分布在不同区域的零售商面对的市场需求是不同的,他们根据所在区域的市场需求进货和出货;经销商根据零售商的订货量进货和出货;生产商根据下游需求生产及出货。现实的供应链系统中,生产商会依据当前的订单量和库存量制定当天的生产计划。
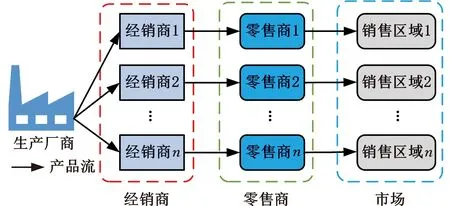
图1 三级网状营销模式示意图
基于图1所示的供应链系统各个环节的产品传递关系,利用供应链系统产品“生产-储存-销售”的企业库存管理基本数量逻辑关系,建立周期性的供应链库存系统动态模型。以供应链系统各个环节的库存量为被控对象,考虑生产商的产量、下游企业进货量与出货量等参数,在一个经销商只对一个零售商供货的情况下,通过等效和简化得到供应链系统上下游企业的库存关系示意图(图2)。图2中,x为生产商的库存水平,u为生产商的产量,pi(i=1,2,…,n)为生产商向经销商i的出货量;zi为经销商i的库存水平,vi为经销商i向零售商i的出货量;mi为零售商i的库存水平,di为零售商i的出货量。

图2 供应链系统的上下游企业库存关系示意图
为准确建立供应链库存系统的模型,以切实反映供应链库存系统的真实情况,做如下假设:
(1)网状营销模式下,所有经销商均只到唯一的生产商取货,并且只向特定区域的零售商供货,不存在串货的情况。
(2)假设生产商的生产计划制定点为kT,其中,k=1,2,…,n,T为生产计划的制定周期。大多数情况下,生产计划的制定周期为“天”。
(3)供应链系统各个环节的库存产品存在库存自损现象。假设供应链库存系统各个环节的周期T内的自损率γ=[γ0γ1…γ2n]T,其中,γ0为生产商的库存自损率,γi为经销商i的库存自损率,γn+i为零售商i的库存自损率。
(4)产品在运输过程中存在一定程度的损耗。假设供应链系统各个环节在产品运输过程中周期T内的运输损耗率δ=[0δ1δ2…δ2n]T,其中,δi为生产商到经销商i的运输损耗率,δn+i为经销商i到零售商i的运输损耗率。
基于以上假设得到供应链库存系统运行示意图(图3)。基于图3和供应链系统产品“生产-储存-销售”的企业库存管理基本数量逻辑关系,得到如下表达式:
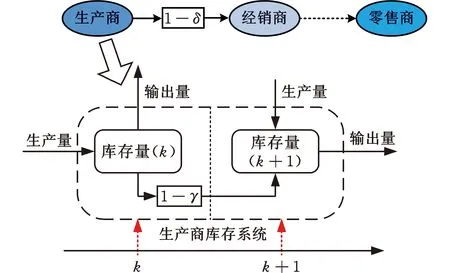
图3 供应链库存系统运行示意图
(1)
对于供应链系统企业管理者来说,企业的库存量、生产量和进货量是比较重要的参数,基于此,本文设:
(2)
通过整合式(1)、式(2)可以得到
X(k+1)=AX(k)+BU(k)+Dd(k)
(3)
其中,矩阵A、B、D为根据式(2)对式(1)进行整合得到的系数矩阵。
综上,我们可以得到三级网状供应链库存系统模型的状态空间基本表达式:
(4)
式中,y(k)为系统可测量的输出量;A~D均为已知的常数矩阵;C为单位矩阵。
供应链库存系统(式(4))为能控能观系统。
针对所构建的三级网状供应链库存系统模型,本文做如下几点说明:①供应链系统各个环节的库存量应小于其最大库存量;②供应链系统某个环节的库存量小于0表示该环节处于短时期的缺货状态;③供应链系统正常运行状态下,市场需求d(k)一般是不会发生改变的。
2 基于自适应指数趋近律的改进型滑模控制
滑模控制算法主要包括滑模面的设计和趋近率的设计。滑模面的设计主要根据系统结构及控制目标。目前,设计方法的趋近律主要为等速趋近律、指数趋近律、幂次趋近律、一般趋近律。为解决传统滑模控制的趋近速度慢和波动较大的缺点,本文引入自适应控制函数对传统的指数趋近律进行改进,提出自适应指数趋近律。基于自适应指数趋近律设计了改进型滑模控制器,在削弱系统抖动的同时能提高系统的响应速度。根据文献[29]得到传统的指数趋近律:
(5)
式中,s为滑模面函数;ε、τ为趋近系数,ε,τ>0。
传统的指数趋近律中,-εsgns为等速项,-τs为指数项。被控对象的系统状态距离滑模面s较远时,趋近律中的指数项、等速项同时起作用,控制被控对象的系统状态逐渐运动至滑模面;被控对象的系统状态接近滑模面s时,指数项偏小,等速项起主要作用。
为解决基于传统指数趋近律的滑模控制的趋近慢和稳定后超调量大的问题,使滑模控制适用于供应链库存系统,本文引入自适应函数q(s),根据系统控制状态自适应调节趋近律,在加快趋近速度的同时消除系统的抖动问题。引入q(s)后的指数趋近律为
(6)
(7)
通过分析可以发现,系统运动点远离滑模面时,s较大,根据式(7)可以得到q(s)会增大,系统的趋近速度提高,控制时长缩短;系统运动点接近滑模面时,|s|趋于0,q(s)<1,q(s)此时的作用是抑制抖动,减小系统稳定之后所出现的波动量。根据式(7)可以发现,随着参数b的增大,q(s)逐渐变小,对库存波动量的抑制更显著。
为进一步减小系统稳定后的抖动,对符号函数进行平滑处理,即令符号函数为
(8)
其中,β=0.01。
3 基于改进型滑模控制和扰动观测器的优化模型
为提高供应链库存系统的鲁棒性和抗扰动能力,结合改进型滑模控制器和扰动观测器,设计了需求扰动作用下的供应链库存系统优化模型。本文将供应链系统的需求扰动分为内部需求扰动和外部需求扰动。对于潜在的内部需求扰动,本节利用改进型滑模控制削弱其对供应链库存系统的影响,使得供应链系统各环节的库存量趋于企业的目标库存量;对于外部需求扰动,通过设计扰动观测器对其进行实时测量跟踪,得到扰动观测量,再利用扰动观测值进行前馈补偿控制,削弱外部需求扰动对供应链库存系统的影响。

(9)
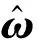

图4 需求扰动作用下的三级供应链库存优化模型原理图
根据图4可知企业的生产量和进货量:
U(k)=Us(k)+Uo(k)
(10)
需求扰动作用下的三级供应链库存系统优化模型的设计主要包括改进型滑模控制器的设计和扰动观测器的设计。
3.1 改进型滑模控制器的设计
控制供应链系统各环节库存量达到企业目标库存量的同时,为削弱潜在的市场需求扰动对供应链库存系统的影响,本文利用改进型滑模控制进行控制器的设计。
设供应链系统各个环节在k时刻的企业目标库存量为
Xd(k)=[xd(k)z1,d(k)z2,d(k) …zn,d(k)
m1,d(k)m2,d(k) …mn,d(k)]T
根据Xd(k)可得供应链系统上下游企业在k时刻的库存误差为
e(k)=Xd(k)-X(k)
(11)
根据式(11)可以得到
e(k)=[e1(k)e2(k) …e2n+1(k)]T
(12)
其中,e1(k)为k时刻生产商的库存误差;e2(k)~en+1(k)为k时刻经销商的库存误差;en+1(k)~e2n+1(k)为k时刻零售商的库存误差。
依托式(11)可以构造k时刻的滑模面:
s(k)=ce(k)
(13)
式中,c为滑模面参数,c=diag(c1,c2,…,c2n+1)。
根据式(12)、式(13)可以得到
s(k)=[s1(k)s2(k) …s2n+1(k)]T
(14)
其中,s1(k)表示k时刻生产商的滑模面,s2(k)~sn+1(k)表示k时刻经销商的滑模面,sn+1(k)~s2n+1(k)表示k时刻零售商的滑模面。
根据构造的滑模面,我们可以进行改进型滑模控制器的设计。
首先,为了方便计算和理解,根据式(8),令
(15)
由式(7)可得本文采用的自适应指数趋近律:
(16)
τ=diag(τ1,τ2,…,τ2n+1)ε=diag(ε1,ε2,…,ε2n+1)
式中,Δt为采样时间。
则由式(16)可得
s(k+1)=-εQ(sk)F(sk)Δt-τΔts(k)+s(k)=
(I-τΔt)s(k)-εQ(sk)F(sk)Δt
(17)
式中,I为单位矩阵。
联立式(11)、式(13)和式(17)可得
X(k+1)=Xd(k+1)+c-1[εQ(sk)F(sk)Δt-
(I-τΔt)s(k)]
(18)
外部需求扰动ω(k)=0时,联立式(9)、式(18)可得改进型滑模控制器:
Us(k)=B-1(Xd(k+1)-AX(k)-Dd(k))+
(cB)-1[εQ(sk)F(sk)Δt-(I-τΔt)s(k)]
(19)
接下来,将对所构建的改进型滑模控制进行稳定性分析。这里主要是通过构建Lyapunov函数进行稳定性证明,其中,构造的Lyapunov函数为
(20)
为了分析改进型滑模控制器的稳定性,这里令
H=[0](2n+1)×1
(21)

(22)
首先,联立式(20)对式(22)进行分析可以得到
V(sk+1)-V(sk)=
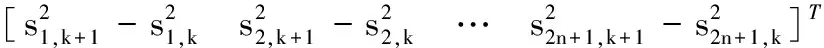
(23)
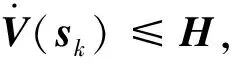

(24)
由式(24)可知,只要
(25)
(s1(k+1)-s1(k))f(s1,k)=[(1-τ1Δt)s1(k)-
ε1q(s1,k)f(s1,k)Δt]f(s1,k)=(-τ1Δts(k)-
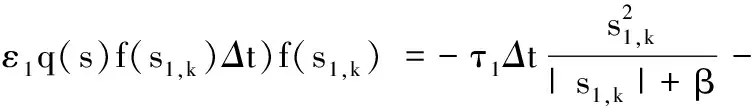
ε1q(s1,k)f2(s1,k)Δt<0
(26)
(s1(k+1)+s1(k))f(s1,k)=[(1-τ1Δt)s1(k)-
ε1q(s1,k)f(s1,k)Δt+s1(k)]f(s1,k)=
[(2-τ1Δt)s1(k)-ε1q(s1,k)f(s1,k)Δt]f(s1,k)=

(27)
通过分析式(27)可以得到
(28)
证毕。
3.2 扰动观测器设计
为能有效地控制供应链系统的外部需求扰动,降低其对供应链库存系统的影响,设计扰动观测器来实时跟踪外部需求的扰动,并利用前馈补偿控制削弱外部需求扰动对供应链库存系统的影响。扰动观测器的设计主要包括扰动观测器的设计和扰动观测器的收敛性分析。扰动观测器的设计原理如图5所示。

图5 扰动观测器设计原理图
(29)
根据前馈补偿机制,可以得补偿控制量:
(30)
联立式(9)、式(16)、式(18)、式(19)、式(29)、式(30)得
s(k+1)=c(Xd(k+1)-X(k+1))=c(Xd(k+1)-
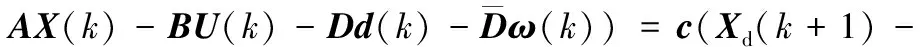
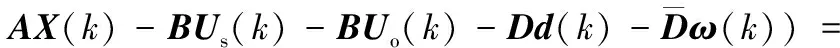
c{(-2AX(k)-Dd(k)-c-1[εQ(sk)F(sk)Δt-
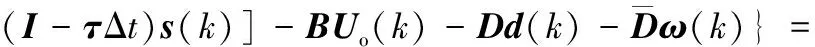
-c{c-1[εQ(sk)F(sk)Δt-(I-τΔt)s(k)]+
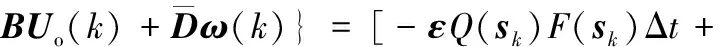
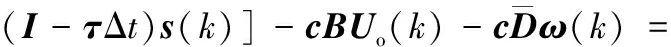

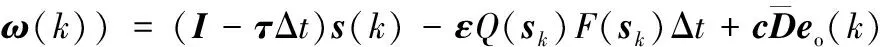
(31)
则根据式(31),将扰动观测量定义为

(I-τΔt)s(k-1)+εQ(sk)F(sk)Δt]
(32)
通过联立式(24)~式(32)可得




ω(k)+e0(k)-e0(k)=ω(k+1)-ω(k)
(33)
设可测量的外部需求扰动的最大变化率矩阵λmax=[λ1,maxλ2,max…λn,max]T,则可以得到
eo(k+1)=ω(k+1)-ω(k)≤λmaxΔt
(34)
λl,maxΔt→0成立时(l=1,2,…,n),eo(k+1)→[0]n×1,这表明本文设计的扰动观测器收敛。扰动观测器稳定时,扰动观测量的大小会逐渐逼近外部需求扰动的大小。
综上,根据扰动观测量可以得到前馈补偿控制量:
(35)
sgnsk-1=[sgns1(k-1) sgns2(k-1) …
sgns2n+1(k-1)]T
至此,供应链库存系统优化模型中的扰动观测器设计完毕。
4 仿真实验对比研究
为体现改进型滑模控制在供应链库存系统优化管理的优越性,并验证供应链库存系统优化模型的有效性及适用性,基于MATLAB/Simulink平台建立了供应链库存系统优化模型并进行仿真对比实验。具体的实验步骤如下:①根据假设的数值确定自损率、运输损耗率、市场需求等参数,构建三级供应链库存系统,搭建的供应链库存系统优化模型主要包括扰动观测器、改进型滑模控制器、三级供应链动态库存系统;②对供应链库存系统优化模型进行参数整定与优化,选取与供应链动态库存系统相匹配的最优控制参数组合,以优化模型的控制效果、提高控制精度;③以供应链库存系统的缺货次数、货物积压次数、库存移动标准差、“生产-储存-销售” 策略和调节时长为控制指标,对仿真结果进行综合对比分析,以验证改进型滑模控制模型对需求扰动作用下的供应链库存系统的控制效果。
4.1 模型的参数整定与优化
对于供应链库存系统优化模型而言,参数整定是至关重要的。良好的控制参数能有效缩短控制时长,提高系统响应速度,减小控制过程中出现的库存波动,实现更优的控制效果。本文利用Simulink平台进行模型参数的整定与优化,以固定库存量为目标库存量、以正弦信号为外部需求扰动进行参数整定测试。本文假设某三级供应链库存系统模型参数如下:
基于本节假设的三级供应链库存系统模型参数,利用MATLAB/Simulink平台搭建的供应链库存系统优化模型如图6所示,其中,供应链库存系统模块根据式(9)构建,改进型滑模控制器模块根据式(19)构建,扰动观测器模块根据式(35)构建。
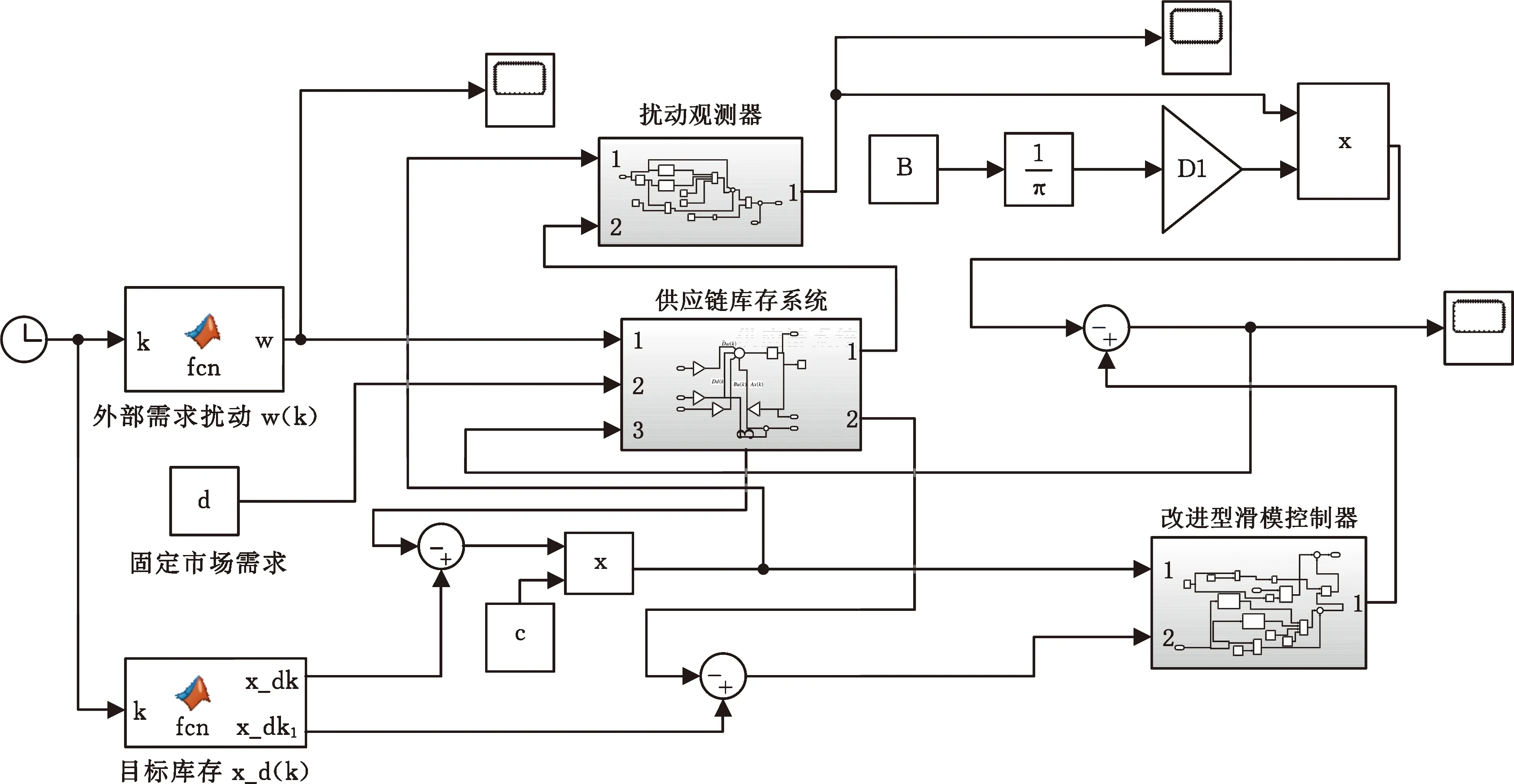
图6 供应链库存系统优化模型仿真框图
供应链库存系统优化模型的初始参数如下:滑模控制的控制参数矩阵c=diag(c1,c2,c3)=diag(30,30,30);自适应指数趋近律q(s)中的参数a=50,b=10;自适应指数趋近律的趋近系数矩阵ε=diag(ε1,ε2,ε3)=diag(0.1,0.1,0.1),τ=diag(τ1,τ2,τ3)=diag(3,3,3)。
初始参数状态下,优化模型对外部需求扰动(正弦信号)的跟踪曲线见图7,可以发现,扰动观测器针在0~10 d对外部需求扰动的跟踪效果比较差,且达到稳定的耗时较长。

图7 初始参数下扰动观测器跟踪效果
初始参数状态下,以零售商的库存量为参考对象,得到供应链库存系统优化模型在固定库存目标条件下的零售商库存,如图8所示。根据图8,通过计算和分析可以得到,初始参数条件下,供应链库存系统优化模型的平均库存误差为93 t,需求扰动作用下的调节时长为6 d。
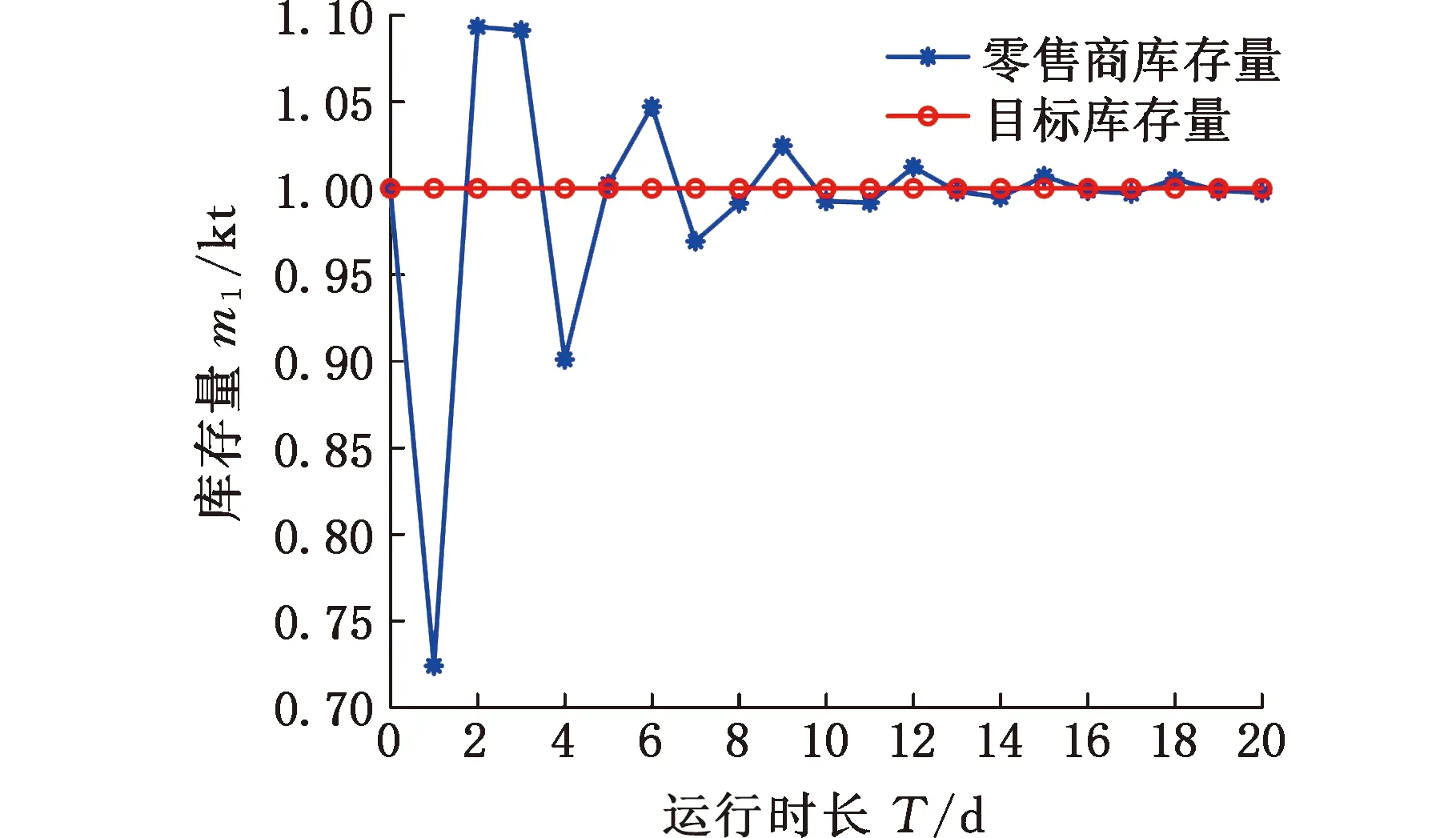
图8 初始参数下零售商库存量变化
为使供应链上下游企业库存系统对需求扰动的响应满足准确、快速的原则,尽量减小供应链系统各个环节的库存波动,对优化模型的不同参数进行整定与优化。大量实验调整后,确定的最优参数组合如下:滑模控制的控制参数矩阵copt=diag(20,20,20);自适应指数趋近律q(s)中的参数aopt=15,bopt=5;自适应指数趋近律的趋近系数矩阵εopt=diag(0.05,0.05,0.05),τopt=diag(2,2,2)。
参数整定后的需求扰动跟踪曲线见图9。与图8相比,可以看到扰动观测器的跟踪速度明显提高,跟踪误差明显减小,震荡幅度明显减小,扰动观测器对需求扰动的跟踪精度和跟踪性能有了较大地提高。
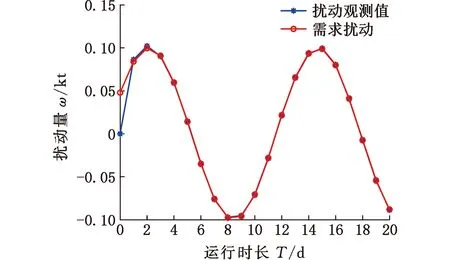
图9 模型参数整定优化后需求扰动跟踪曲线
参数整定后,供应链库存系统优化模型在固定库存目标条件下的零售商库存变化如图10所示。参数整定后,调节时长缩短为2d,稳定后的库存波动减小了,系统的控制效果较好。

图10 模型参数整定优化后零售商目标库存跟踪曲线
4.2 仿真对比研究
基于参数整定后的供应链库存系统优化模型进行正常情况(无外部需求扰动)和需求扰动作用下供应链库存系统优化前后的仿真对比实验。为体现改进型滑模控制的优越性,对正常情况下的供应链库存系统仿真分别进行滑模控制(sliding mode control,SMC)和改进型滑模控制(improved sliding mode control,ISMC)的实验。三级供应链库存系统的模型参数与参数整定优化实验一致,其中,供应链库存系统各环节在k时刻的目标库存量Xd(k)=|sin(kΔt)|·[1.02 0.94 0.52]T,固定市场需求d=[0 0 0.43]T,k时刻的外部需求扰动ω(k)=[0 0 0 ±0.26sin(kΔt)]T。
假设该三级供应链系统以“天”为周期制定“生产-储存-销售”计划。为更切实地模拟复杂市场环境下的外部需求扰动,实验过程中分别在第5天、35天施加持续时间为15 d的需求扰动,其中,第5天施加正需求扰动即需求量增加,第35天施加负需求扰动即需求量减少。在上述仿真条件下,通过对比分析仿真实验的结果来验证优化模型的有效性。
在不同仿真实验条件下,供应链系统生产商、经销商和零售商的库存量仿真结果如图11~图13所示。
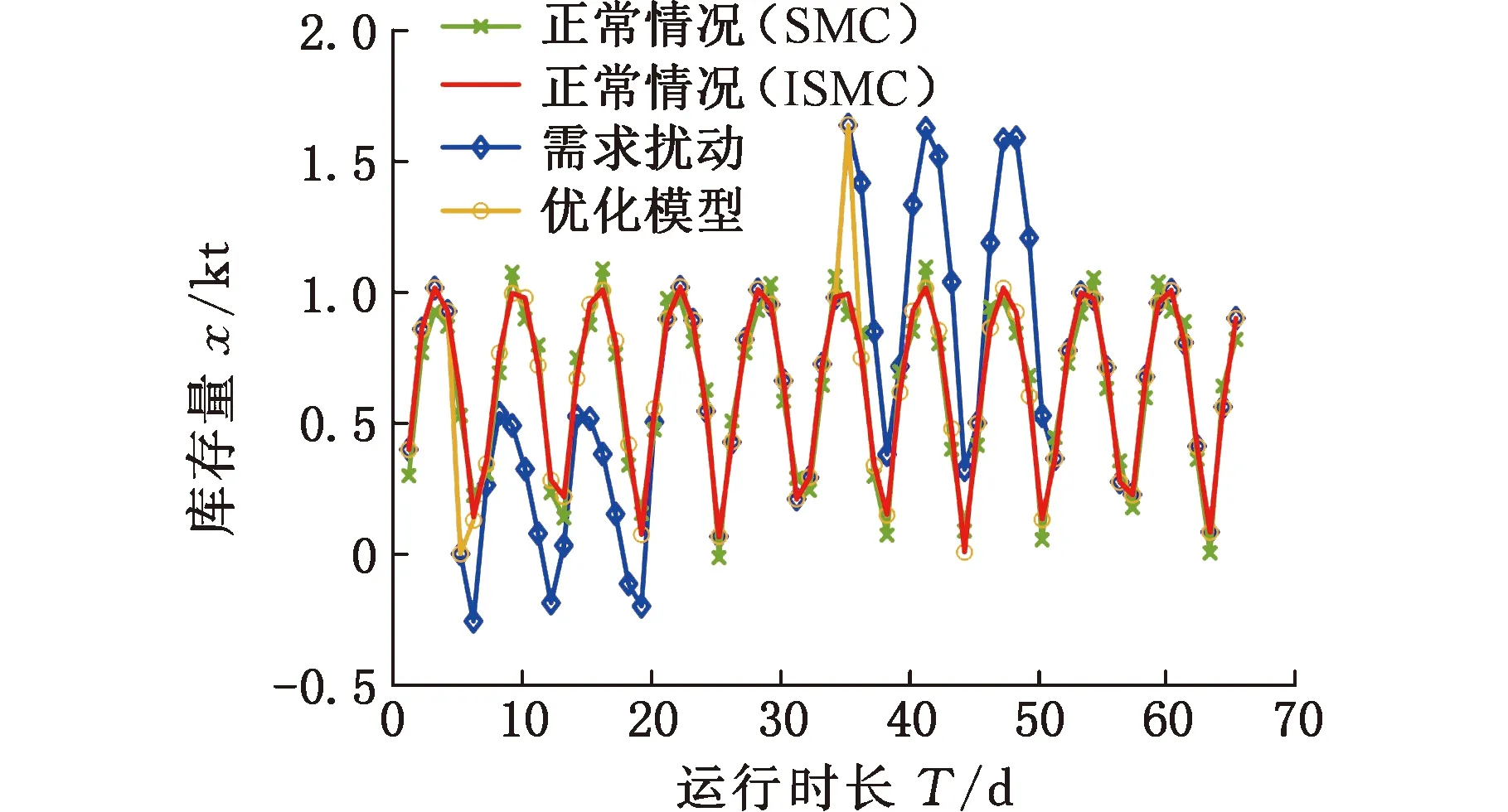
图11 生产商库存量
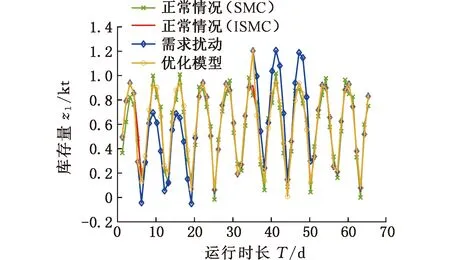
图12 经销商库存量

图13 零售商库存量
根据仿真实验得到的库存量,从缺货次数、货物积压次数和库存移动标准差对仿真结果进行综合分析,其中,企业库存量小于0的状态定义为缺货,企业库存量超过最大目标库存量50%的状态定义为货物积压。供应链库存系统运营过程中,通过每个采样点的库存标准差得到库存移动标准差。根据上述定义得到三级供应链库存系统的缺货次数和货物积压次数,如表1所示。
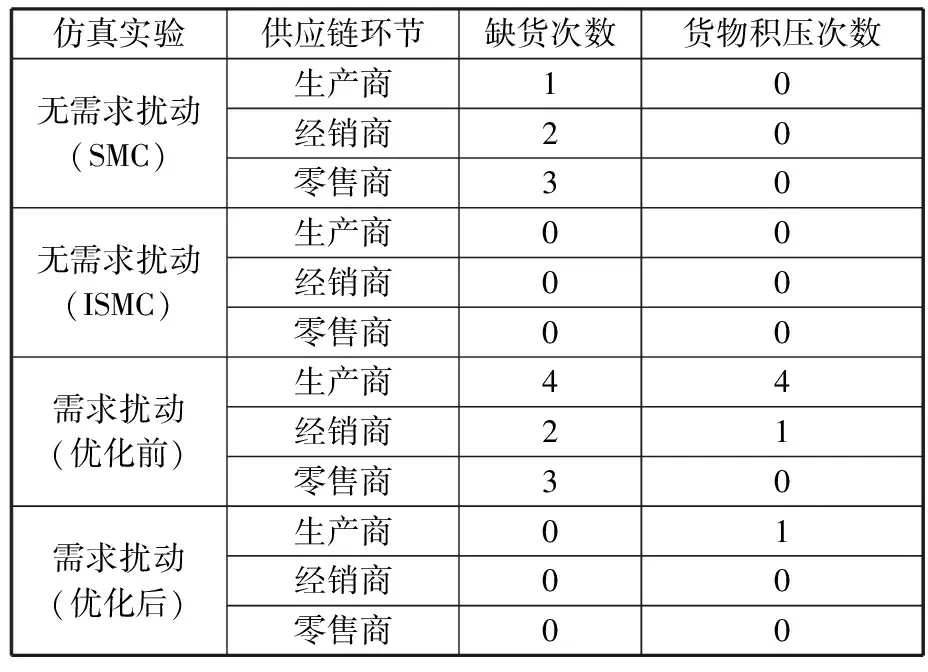
表1 相关控制指标
由表1可以看出,需求没有扰动时,SMC会引起库存波动,导致供应链系统各环节出现不同程度的轻微缺货问题;ISMC时,供应链系统各个环节则不会出现缺货和货物积压问题。这说明ISMC能减小企业库存波动,有更好的控制效果。通过分析需求扰动下的供应链库存系统货物存贮状态可以发现,由于需求扰动的存在,生产商分别出现了4次缺货及货物积压问题,经销商与零售商也出现了不同程度的缺货与货物积压问题。本文提出的优化模型能提高供应链库存系统的抗扰动能力,稳定供应链上下游企业的库存量,解决供应链系统各个环节的缺货及货物积压问题。
库存移动标准差能反映供应链系统不同环节的库存波动趋势。不同仿真的供应链系统各环节库存量移动标准差如图14~图16所示。
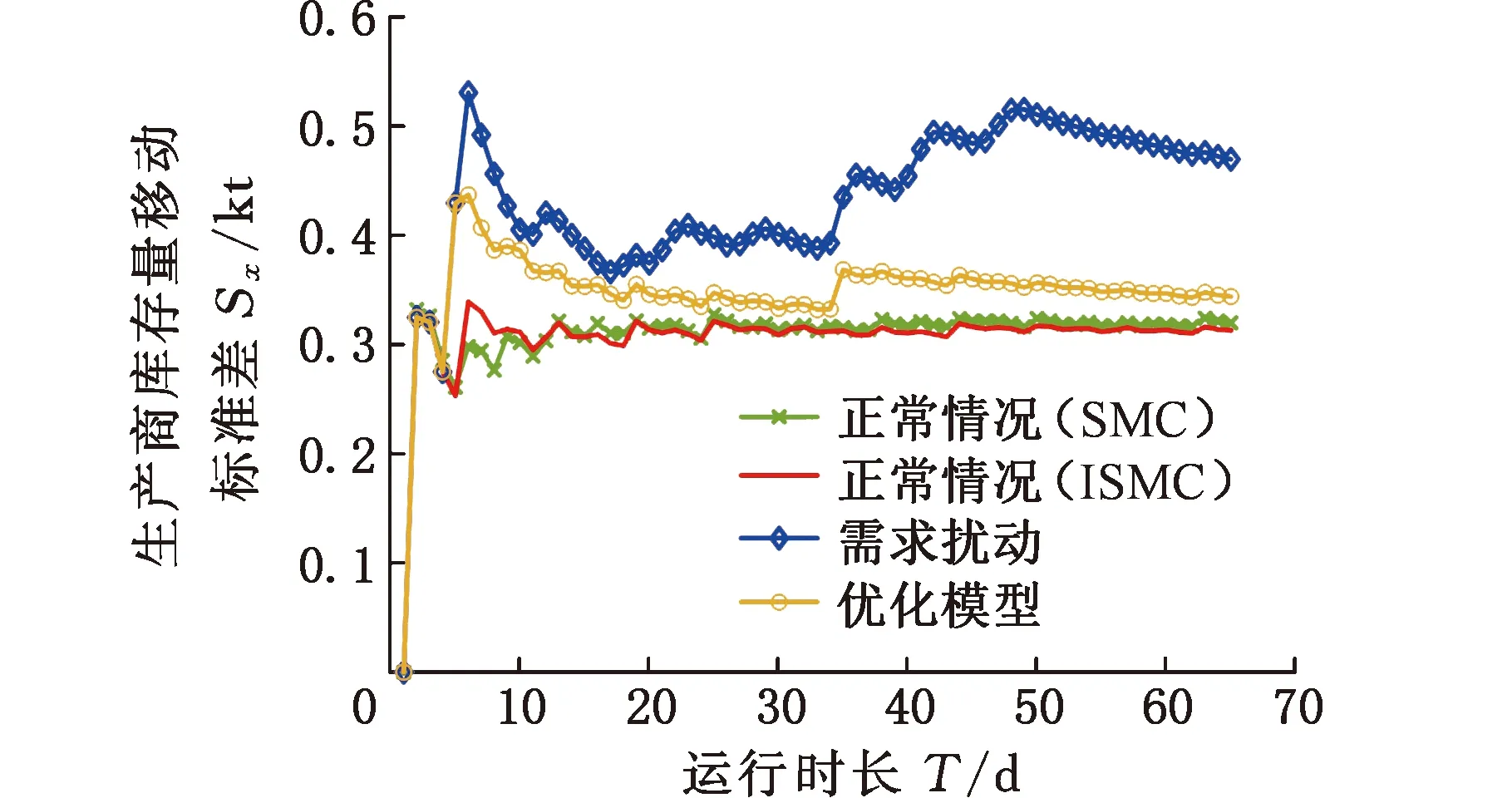
图14 生产商库存量移动标准差
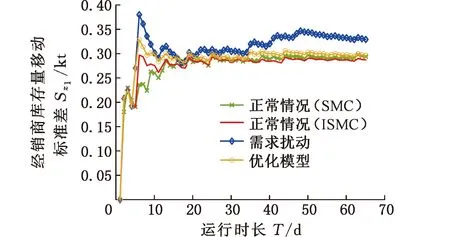
图15 经销商库存量移动标准差

图16 零售商库存量移动标准差
由图14~图16可知,在供应链系统企业库存量趋于目标库存量的阶段(0~5 d),SMC的库存移动标准差小于ISMC的库存移动标准差,这说明在趋近目标库存阶段,ISMC有更高的系统响应速度和趋近速度。供应链库存系统稳定之后,SMC的库存移动标准差大于ISMC的库存移动标准差,这说明ISMC在稳定阶段(10~65 d)的控制效果更好、库存波动更小。分析外部扰动作用下的仿真实验移动标准差可以得到,优化模型能减小需求扰动对供应链上下游企业库存系统的影响,增强了供应链库存系统的鲁棒性,减小库存波动,使的企业库存量处于相对稳定的状态,有效降低了企业的库存运营成本。
无论是生产商生产量还是经销商和零售商的进货量均是不小于0的,基于此,输出结果中,当企业生产量或进货量小于0的时候令其等于0,则可得到需求扰动作用下生产商的生产量以及经销商和零售商的进货量的仿真结果,如图17所示。分析图17可以发现,供应链库存系统优化模型能帮助各环节制定良好的“生产/进货-储存-销售”策略,主动消除需求扰动对供应链库存系统的影响,并且以最低的生产水平满足市场需求。
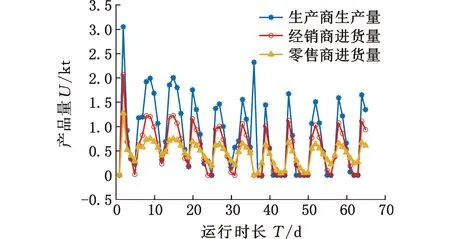
图17 优化模型情况下各环节的生产量/出货量
为比较优化模型对需求扰动的应对速度,通过分析供应链系统各环节的库存误差(图18),得到2次需求扰动作用时优化模型的调节时间。由表2可以看出,对于作用时长15 d的市场需求扰动,供应链库存系统优化模型的调节时间控制在4d以内,零售商更是能在1 d内有效应对需求扰动,这反映出优化模型具有较好的系统反应速度,提高了供应链库存系统对突发性扰动的应对能力,帮助供应链系统上下游企业适应复杂的市场环境。

表2 需求扰动调节时长
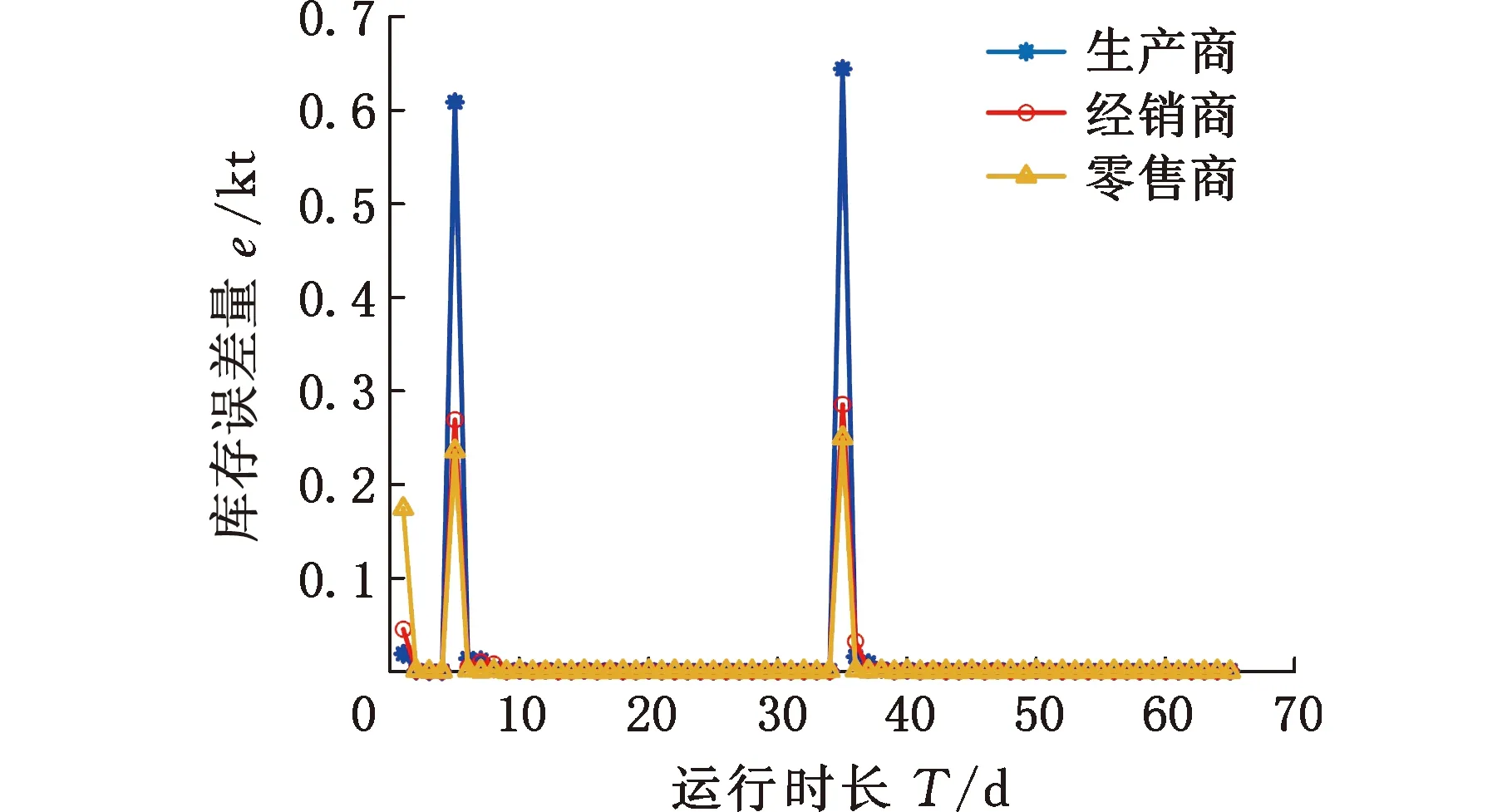
图18 优化模型情况下各环节库存误差
综上,通过5个控制指标对不同仿真结果进行综合分析可以得到:ISMC在供应链库存系统管理优化方面有着更好的控制效果;优化模型能提高供应链库存系统的鲁棒性和抗扰动能力,在需求扰动作用下帮助企业制定合理的“生产/进货-储存-销售”策略,减小需求扰动引起的库存积压、缺货及库存波动等问题,减少供应链系统各环节库存资源浪费,有效提高供应链库存系统对突发性扰动的应对能力,快速应对市场的需求扰动。
5 结论与展望
为提高供应链库存系统的鲁棒性和抗扰动能力,对需求扰动下的供应链库存系统优化管理问题进行了深入研究和仿真实验。仿真实验结果表明:①相较于传统的滑模控制,提出的改进型滑模控制在供应链管理优化有更优的控制效果;②优化模型能增强供应链库存系统的鲁棒性和抗扰动能力,对需求扰动具有较高的反应速度和较好的补偿控制效果;③优化模型能在短时间内指导企业制定科学合理的“生产/进货-储存-销售”策略,在消除缺货的基础上,减少企业库存,保证供应链库存系统稳定运行。
本文设计的供应链库存系统优化模型仿真实验中,供应链库存系统模型是简化的,未来可研究完整的网状供应链库存系统。除此之外,文中的供应链库存系统模型是线性的,而现实环境存在诸多非线性因素,因此未来可以加入非线性关系并进行深入研究。
