采用改进两点交叉算子的改进自适应遗传算法求解不相关并行机混合流水车间调度问题
2023-08-08练志伟顾新艳朱长建冯雪晴
郑 堃 练志伟 顾新艳 朱长建 徐 慧 冯雪晴
1.南京工程学院汽车与轨道交通学院,南京,2111672.中德智能制造研究院,南京,211800 3.大全集团有限公司,镇江,212211
0 引言
混合流水车间调度问题[1](hybrid flow-shop scheduling problem, HFSP)拓展了经典流水车间调度问题,具有很高的研究价值和广阔的应用前景。在以最大完工时间最小化为目标的情况下,HFSP一般指的是已知各工件加工时间,确定各工件的加工顺序以及各阶段上工件被优化分配机器的情况,是一个典型的NP-Hard问题。HFSP被分为三种类型:相同并行机、均匀并行机和不相关并行机[2],其中,不相关并行机混合流水车间调度问题(hybrid flow-shop scheduling problem with unrelated parallel machine, HFSP-UPM)指某个加工阶段的加工时间取决于加工工件与加工机器的匹配程度,因问题模型应用更为广泛,而受到学者越来越多的关注。
目前求解HFSP-UPM以元启发式方法为主,通过借鉴自然界的规律,可以很好地求解调度问题,常用的算法有遗传算法(genetic algorithm, GA)[3]、基于激素调节机制的改进粒子群优化(particle swarm optimization, PSO)算法[4]、变邻域搜索混合的果蝇优化算法(fruit fly optimization algorithm, FOA)[5]、人工蜂群(artificial bee colony, ABC)算法[6]、分布估计算法(estimation of distribution algorithm, EDA)[7]、离散化的蜻蜓算法(dragonfly algorithm, DA)[8]等。GA应用广泛,但自身算子设计限制及参数选择影响了应用效果。从元启发式方法的研究现状来看,算法混合是提高求解性能的必要手段。薛玲玲[9]在GA的基础上混合块结构的邻域搜索,以突出GA的局部开发优势,解决GA早熟等问题。吴树景等[10]将GA、变邻域搜索方法与精英保护策略结合,提出运算效率和求解性能均佳的混合算法。轩华等[11]结合NEH启发式方法、局域搜索和GA的结构优势来提高混合GA求解的质量。虽然混合算法能提高求解的性能,但会导致算法的复杂度高和扩展性低,因此算法自身的优化成为当前的热点研究方向[12]。
针对GA自身算子参数选择困难等缺陷,王雷等[13]受人体系统中激素调节规律的启发,将激素调节机制应用至GA的交叉和变异参数设计中,提出了基于激素调节机制的改进型自适应遗传算法(improved adaptive genetic algorithm, IAGA),通过激素调节的自适应参数,使得算法在中后期具备较强的精细化搜索能力,从而提高算法的收敛性能。文献[4]将激素调节机制应用至PSO的惯性因子w,实验表明激素调节机制可增强算法的求解效率。文献[14]针对激素调节规律在目标函数较大时出现失调的现象进行深入研究,提出激素调节的选择概率及改进两点交叉算子(improved two-points crossover, ITPX),并通过标准算例验证了所提算法的综合性能。激素调节机制和ITPX可有效提高算法性能,但激素调节选择概率与ITPX的性能对算法有何种影响尚未进行深入研究,结合激素调节机制进一步增强ITPX和算法的收敛性也需进一步深入分析。
本文在前述研究基础上,提出基于改进两点交叉算子的改进自适应遗传算法(ITPX-IAGA),并将该算法应用于复杂的HFSP-UPM。本文具体工作如下:①阐述了ITPX的理论,细化ITPX的发展过程及依赖性,从解的质量和时间的消耗两个不同维度对其性能进行定性和定量分析;通过实验论证了ITPX解决传统TPX缺陷的效果及其在算法中后期的探索与开发能力;②利用工程算例验证了基于激素调节机制的自适应选择概率,论证其对算法收敛性的影响。
1 混合流水车间调度问题
1.1 符号说明
为更好描述HFSP-UPM,给出了符号及其释义,如表1所示。
1.2 问题描述
HFSP-UPM描述如下:n个相互独立工件{J1,J2,…,Jn}需经过s个加工阶段,每个阶段有mk台加工机器{M1,M2,…,Mmk}可供选择,每个工件在每个阶段的加工时间可能不同;调度目标为优化工件在每个阶段加工机器的选择以及在机器上的加工顺序,使得所有工件的最大完工时间Cmax最小,图1为该问题的示意图,并做出如下约束:①初始时刻,所有工件和加工机器准备就绪;②流水线具有固定的顺序,所有工件需以相同的顺序经过每个加工阶段;③每个阶段至少存在一台加工机器,并且至少有一个阶段存在多台加工机器;④一个工件在每阶段不同机器上的加工时间可有所不同;⑤工件在每个阶段只可选择一台机器进行加工;⑥任意时刻一台机器只可加工一个工件;⑦机器一旦开始加工,就不能中断。
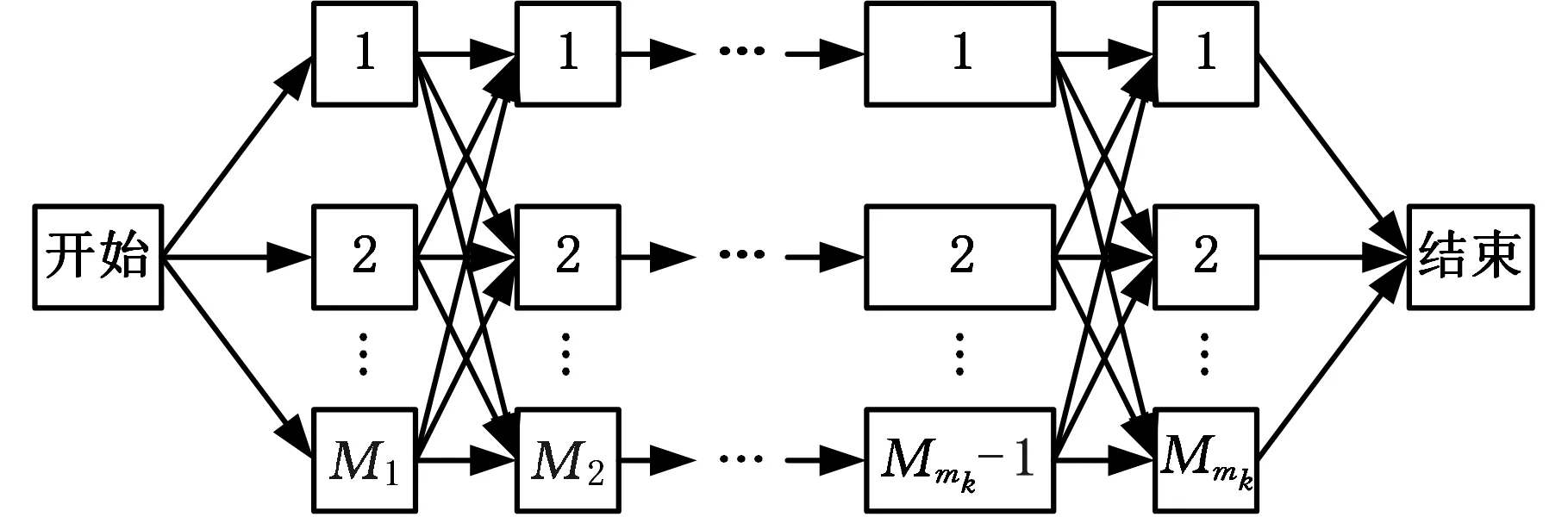
图1 HFSP-UPM示意图
1.3 模型建立
HFSP-UPM的数学模型如下:
Cmax=min(max{C(k,i)|i=1,2,…,n;
k=1,2,…,s})
(1)
(2)
(3)
C(k,i)=S(k,i)+P(k,j,i)
(4)
(5)
S(k+1,i)-S(k,i)≥P(k,j,i)
(6)
Yki1i2+Yki2i1≤1
(7)
S(k,i1)-C(i2,k)+L(3-Yki2i1-Xi1kj-Xi2kj)≥0
(8)
i=1,2,…,ni1≠i2
k=1,2,…,sj=1,2,…,mk
式中,L为足够大的常数。
式(2)、式(3)分别为任意工件选择机器和加工顺序的变量约束;式(5)表示任意工件在任意阶段只能选择一台加工机器进行加工;式(6)表示任意工件只有完成上一阶段的加工任务后才能开始下一阶段的加工任务;式(7)、式(8)表示一台机器在某一时刻只可加工一个工件。
2 应用ITPX的IAGA
2.1 ITPX-IAGA流程
ITPX-IAGA流程如图2所示,具体过程如下:
(1)设计算法参数;
(2)生成初始种群;
(3)计算自适应参数(自适应选择概率Po、自适应交叉概率Pc、自适应变异概率Pm)和初始化或更新染色体池,若满足最大迭代次数,则输出记忆因子携带的信息,并且退出运行,否则转至步骤(4);
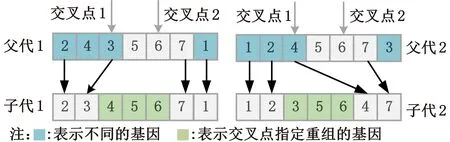
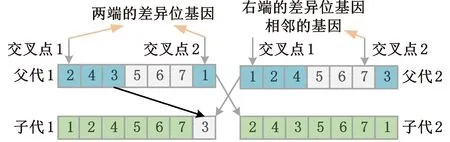
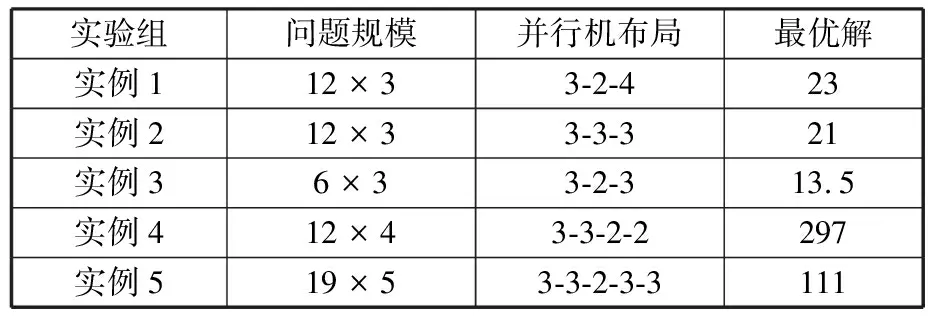
(4)执行ITPX交叉流程,若随机概率P (5)执行变异流程,若P (6)迭代新种群,并跳转步骤(3)。 受内分泌激素基本规律[15]的启发,文献[13-14]设计了与种群优劣程度相关的自适应选择概率、交叉概率和变异概率因子函数,具体如下。 自适应交叉概率[13]: Pc= (9) 自适应变异概率[13] Pm= (10) 自适应选择概率[14] Po= (11) 2.3.1染色体编码 U=(U1,U2,…,Un)表示工件集在第一阶段的加工顺序,U的元素为工件号,如U=(1,4,3,5,2)对应工件的加工顺序为J1→J4→J3→J5→J2。 2.3.2染色体解码 HFSP解码分为工件排序和机器分配,工件排序方式为先到先处理。第一个加工阶段,工件按照染色体编码顺序安排加工;其他加工阶段,按照工件到达该阶段的顺序安排加工机器,若到达顺序相同则随机排序。 机器分配方式如下:比较工件i在此阶段上机器j的释放时间rj和工件i上一阶段的完工时间C(k-1,i),取最大值为工件i在机器j上的最早开始加工时间aj即aj=max(rj,C(k-1,i)),计算工件i在此阶段每个可选机器上的值{aj+P(k,j,i)},选取其中具有min{aj+P(k,j,i)}的机器作为工件i在此阶段的加工机器,若有最小值相同的机器,则随机选择。 2.3.3初始化方法 本文采用的反向学习法(opposition-based learning, OBL)[16]设工件号为1、2、…、n,若某加序的编码为Ui,则Ui的反向学习编码为 U′i=1+n-Ui (12) 因此本文的初始化过程如下: (1)设置初始种群个体数为N,生成初始种群P1。按式(12)对种群P1中的所有染色体进行反向学习,生成初始种群P2。 (2)合并种群P1和P2,按照目标函数值从小到大的顺序进行排序,然后选取合并种群中的前N个染色体作为初始种群。 2.3.4适应度函数 本文适应度的计算方法分为两个部分:①将染色体解码的目标函数值Makespan作为该染色体的适应度,即f1=min{Cmax(U)},此方法用于比较个体之间的优劣,f1越小代表该染色体的适应能力越强;②计算自适应选择概率、交叉概率和变异概率时,种群中染色体的适应度f2=1/min{Cmax(U)}[13-14],以保证激素调节规律在GA中的应用效果。 2.3.5选择操作 GA的选择算子通过筛选种群进化过程中的个体来影响种群的进化结果。在种群进化前期,选择算子使高性能个体以更大的概率生存,有利于种群向优质个体区域快速收敛;在种群进化后期,控制高性能个体的遗传有利于保持种群多样性。基于激素调节的选择概率可满足GA迭代中的需求,进一步提高算法的收敛性能。本文采用GOLDBERG等[17]提出的锦标赛选择方法,并设置由激素调节的选择概率Po,随机从种群中选出若干个体,并标记其中具有最小f1(最优)和最大f1(最劣)的个体;若随机概率P 2.3.6交叉操作 交叉是GA全局优化的主要手段,通过对2个匹配父代基因的重新组合高效搜索解空间,因此对GA的优化性能有巨大影响。匹配机制及父代之间的交叉操作存在诸多问题,如匹配的父代是同一染色体、交叉重新组合的基因具有一致性等问题,这使得GA易出现全局收敛慢、解的质量不理想或局部收敛等现象。 排列编码方式通常采用两点交叉算子(two-points crossover, TPX)[14,18]产生子代,如图3所示。TPX产生的子代性能与交叉点的选取关系紧密。选取交叉点的结果如图4所示时,子代个体与父代相同,因此随机取点的方式会导致重组基因一致,使TPX存在冗余度高、效率低和无法高效搜索解空间等缺陷。因此,如何取点让TPX产生有效子代成为提高算法性能的重要途径之一。研究发现,TPX的交叉点在选取时,必须包含2条父代基因中的差异位且不能囊括所有差异位的基因(2条父代在等位比较下不同的基因)或两端差异位中任意相邻的基因,这样才能产生有效子代。如图5所示,交叉点包含所有差异位的基因或右端的差异位基因相邻的基因,使得父代与子代一致。因此,匹配父代是同一或相似染色体时,ITPX不产生任何无效子代,从而提高算法效率。 图3 TPX算子 图5 TPX产生子代与父代相同的取点方式 根据上述ITPX取点的要求,设2个交叉点n1和n2(n1为左交叉点,n2为右交叉点)。产生有效子代的具体实现方法如下: (1)如图6所示,从首端开始比对2条父代之间的基因,并标记差异位的基因,直至末端结束,其中,首端基因位为n1必取的点,末端基因位为n2必取的点。以n1进行中心取点时,n1的可取点只能是差异位基因区域中的点,此时固定n1的取点,则对应的n2根据ITPX产生有效子代的要求进行取点;同理可得以n2为中心的取点方式。 图6 TPX算子的精确交叉取点方式 (2)首先以n1为中心进行取点,n1可取G1、G2和G3。n2根据图5中的约束进行取点,即n2取点不能使重组基因囊括所有差异位的基因或两端差异位中任意相邻的基因,因此n2右端点为G5。n2左端点由当前n1及当前n1从左向右的相邻点是否均属于差异位的基因区域来决定。如图6所示,当前的n1(G1)及当前的n1(G1)从左向右的相邻点(G2)均属于差异位的基因区域时,将当前的n1(G1)作为n2的左端点;同理,当前的n1(G2)可作为n2的左端点,而当前的n1(G3)不作为n2的左端点时,n2左端点为当前的n1(G3)从左向右的相邻点(G4)。对应n2的取点按照父代从左向右的顺序,由n2左端点开始至右端点处结束。 (3)以n2为中心进行取点,除去步骤(2)中n1取过的点(G1、G2和G3)外,n2可取G7。n1则根据图5中的约束进行取点,即与步骤(2)中n2可取点的机制类似,因此n1左端点为G3。n1的右端点由当前的n2及当前的n2从右向左的相邻点是否均属于差异位的基因区域来决定。同样地,从图6可以发现,当前的n2(G7)属于差异位的基因区域,但当前的n2(G7)从右向左的相邻点(G6)却不属于差异位的基因区域,所以当前的n2(G7)不作为n1的右端点,则n1的右端点为当前的n2(G7)从右向左的相邻点(G6)。对应n1的取点按照父代从右向左的顺序,由n1右端点开始依此递进至n1左端点处结束。 综上,本文改进现有TPX的取点方式,进而设计出精确取点的ITPX,通过尽可能地产生2父代的全部有效子代,然后从各自子代集选取性能最优的进入下一次迭代,并利用记忆因子实时监测这一过程,避免最优染色体的丢失。除此之外,建立优质染色体池,实现与种群不同区域的交叉:①2条父代染色体分别从优质染色体池中随机选取和从种群中按选择操作选取,然后以Pc概率交叉;②2条父代染色体均按选择操作从种群中选取并以1-Pc概率交叉。 2条染色体等位比对不同基因的个数称为海明距离H。不同基因数越多,相似度越低,H越大,因此ITPX只有在2条父代相似度较低时,即H较大才具有很强的全局搜索能力,所以在种群进化的后期保持种群多样性十分重要。 2.3.7优质染色体池 本文在交叉算子中引入优质染色体池并利用记忆因子记录种群迭代中出现的优质解,保证优质解的遗传。优质染色体池构成如下: (1)记忆因子。记录交叉算子中所有父代产出的子代和变异算子中特定的扰动,若有优于记忆因子携带的染色体,则更新记忆因子。 (2)初始化。设优质染色体池容量为NP。染色体池前NP/2的容量由初始化种群按照适应度从小到大的排序进行填充,剩余容量按更新策略填充;记忆因子标记其中性能最优的染色体。 在心肌梗塞患者治疗期间,按照相关要求测量患者的血脂和血糖指标,定期监测患者的血压和心电图的变化。吸烟的判定标准为现在吸烟,并且吸烟史在超过3年,每天吸烟超过20支,原发性高血压和糖尿病的判定标准为WHO公布的诊断标准,血脂异常的判定标准参照防治建议[1]。 (3)更新策略。①染色体池有剩余容量时,将种群个体与染色体池中最劣个体比较,若优于最劣个体且染色体池无此适应度的个体,则将此种群个体放入染色体池,否则计算两者的H,若H=0,则不填充,否则填充;② 当染色体池没有剩余容量且满足①中的填充要求时,则替换优质染色体池中的最劣个体。 2.3.8变异操作 扰动操作:①打乱互换,随机选择染色体的不同基因,然后打乱,重新组织;②插入,随机将染色体中的一个基因插入到另一个基因的左侧;③反转逆序,随机反转逆序2个不同基因之间所有基因;④两点互换,随机选择染色体的2个不同基因,并互换。 变异:取随机整数r∈{0,1,2,3},若r=0,则执行扰动①;若r=1,则执行扰动②;若r=2,则执行扰动③;若r=3,连续执行扰动④n次,并利用记忆因子监测此过程。 2.3.9算法复杂性分析 (13) 其中,Ev1是以n1为中心取点时n1可取点的数量;L1d为当前的n1取点时n2可取的左端点基因位置,d=1,2,…,Ev1;Lright为2条父代右端不同的基因位置。 ITPX交叉点以n2为中心时,2条父代的取点次数为 (14) 其中,Ev2是以n2为中心取点时n2可取点的数量;L2d为当前的n2取点时n1可取的右端点基因位置,d=1,2,…,Ev2;Lleft为2条父代左端不同的基因位置。 为验证本文算法性能,使用文献[7-8,20]中的5个工程实例进行测试,如表2所示,其中,实例1有12个工件、3阶段(规模12×3)。建立18个中大规模的随机算例(参数见表3)进行测试。使用最佳相对误差δBRE、平均相对误差δARE和最差相对误差δWRE评价本文算法结果: 表2 实例测试集 表3 随机算例的参数设置 (15) (16) (17) 式中,LB为问题已知的最优值;Cbest、Cavg、Cworst分别为算法在规定次数内求解算例得到的最优值、平均值和最差值。 误差越小表示该算法的性能越好。 改进的遗传算法采用DEV C++编程,程序在Intel Core 主频2.3GHZ、内存8GB的PC上运行。为验证本文所提算法的性能,将开展以下实验: ITPX与TPX的对比实验(实验1)。对比GA采用ITPX和TPX得到解的质量。实验选择实例5进行测试,因为变异算子会提高算法性能、增强交叉算子对算法性能的影响,故将ITPX对比实验分为不带变异的ITPX比较实验和带变异的ITPX比较实验,前者注重ITPX本身的开发性能,后者侧重在变异算子下ITPX的探索性能。相关实验参数如表4所示,每次实验均独立运行20次。 表4 ITPX比较实验参数 基于激素调节的自适应选择概率对比实验(实验2)。由于自适应交叉概率和变异概率已在文献[13-14]中验证,因此本文只对自适应选择概率Po进行对比测试,对比GA采用自适应Po和固定值Po得到解的质量。为客观评价自适应选择概率对整体算法性能的提升提供依据。实验选择实例5进行测试,实验参数如表5所示,自适应Po的参数如表6所示,每次实验均独立运行20次。 表5 自适应选择概率比较实验参数 表6 ITPX-IAGA实验参数 ITPX-IAGA对比实验(实验3)。利用5个工程实例比较ITPX-IAGA与其他几种算法,每次实验均独立运行10次。利用18个中大规模随机算例比较ITPX-IAGA与TPX-IAGA,每次实验均独立运行20次。为客观评价ITPX-IAGA性能,选择表6所示的实验参数。 为验证ITPX对算法性能的影响,对ITPX进行了不带变异和带变异的比较实验(ITPX和TPX采用同一初始种群)。由2.3.9节可知,在GA的进化过程下,TPX的总交叉次数远多于ITPX的总交叉次数。比较实验的统计结果如表7~表9所示。表7、表8中,tI为ITPX的运行时间,t为TPX的运行时间;表9中,tav为20次实验独立运行的平均时间。由表7可发现,ITPX、TPX能找到的最优解分别为111和114;在20次实验中,ITPX、TPX的平均值分别为115.75和116.10;在运行时间上,90%以上的tI小于t。由表8可发现,ITPX、TPX的最优解均为112,但ITPX和TPX求得最优解112的概率分别为25%和5%;在20次实验中,ITPX、TPX的平均值分别为113.5和114.1;运行时间上,tI均小于t。由表9可发现,不带变异ITPX与带变异ITPX的δARE差值为2.4,不带变异的TPX与带变异的TPX的δARE差值为1.8;ITPX的平均运行时间均远小于TPX的平均运行时间,因此可见,与TPX相比,ITPX对解的探索与开发效率更高,在变异的作用下,ITPX的求解性能更优。 表7 不带变异的ITPX比较实验统计结果 表8 带变异的ITPX比较实验统计结果 表9 ITPX的相对误差 由图7、图8可以发现,ITPX整体的收敛性均优于TPX,因此ITPX能有效提高算法求解的效率。 图7 不带变异的ITPX与TPX平均适度收敛曲线图 图8 带变异的ITPX与TPX平均适度收敛曲线图 由文献[13-14]可知式(9)~式(11)中的fav为激素浓度,fmax-fmin为阈值。种群迭代初始阶段中,激素浓度、阈值、激素浓度与阈值的比值产生较大变化将导致自适应参数波动;种群迭代中后期内,种群趋于收敛使得自适应参数波动的需求减小。因此,在种群初期,自适应参数Po具有不固定上限;在种群中后期,自适应参数Po具固定下限特性。 对于实例5,Po不固定上限0.90左右,Po固定下限Po,dow为0.437 55。为验证自适应选择概率Po对算法性能的影响,分别取Po的上限Po,top=0.90、下限Po,down=0.44与Po进行对比实验。对比实验的统计结果如表10~表12所示。表10、表11中,X为自适应参数Po下算法得出的解,Y为Po,top或Po,down下算法得出的解,tX为X的运行时间,tY为Y的运行时间。在表12中,tav为20次实验独立运行的平均时间。由表10可以发现,X、Y的最优值分别为111和113;20次实验中,X、Y的平均值分别为113.75和114.2。由表11可以发现,X、Y的最优值分别为112和111,但Y的最优值111只出现1次(112出现4次),而X的最优值112出现7次;20次实验中,X、Y的平均值分别为113.15和113.65。由表12发现,X的δARE均优于Y;Po,top=0.90时,X的δARE小于Y,X的tav略大于Y;Po,down=0.44时,X的δARE小于Y,X的tav略小于Y。因此Po在运行时间上无明显优势,但在求解的性能优于Po,top或Po,down下的算法。 表10 Po,top=0.90的对比实验统计结果 表11 Po,down=0.44的对比实验统计结果 表12 自适应选择概率相对误差 由图9、图10可以发现,不管是Po,top还是Po,down,自适应Po下解的收敛性都要更优,且收敛也较快。由图11可以发现,自适应Po的上限具有微小的波动,直到收敛于稳定下限0.437 55。Po的对比实验证明自适应参数Po能有效提高算法的搜索质量。 图9 Po,top =0.9与Po下的平均适应度收敛曲线图 图10 Po,down=0.44与Po下的平均适应度收敛曲线 图11 平均自适应参数Po变化曲线(Po,top=0.9,Po,down=0.44) 3.4.1工程实例测试 对于实例1,将ITPX-IAGA与ABC[6]、FOA[20]、GA[21]、差分进化(differential evolutionary, DE)算法[22]和改进差分进化(improved differential evolutionary, IDE)算法[23]进行比较,其中,GA、DE、FOA和ABC的评价次数为10 000,IDE的评价次数为200。所有算法均独立运行10次,实验结果的误差如表13所示。 表13 基于实例1的算法结果的误差 对于实例2,将ITPX-IAGA与EDA[7]、GA[21]和引力搜索算法(gravitational search algorithm, GSA)[24]进行比较,其中,GA和EDA的评价次数为10 000,GSA的运行时间不超过10 s。所有算法均独立运行10次,实验结果的误差如表14所示。 表14 基于实例2的算法结果误差 对于实例3,将ITPX-IAGA与FOA[20]、种群增量学习(population-based incremental learning, PBIL)[23]、改进分布估计算法(improved estimation of distribution algorithm, IEDA)[23]和IDE[23]进行比较,其中,PBIL、IEDA和FOA的评价次数为3000,IDE的评价次数为200。所有算法均独立运行10次,实验结果的误差如表15所示。 表15 基于实例3的算法结果误差 对于实例4,将ITPX-IAGA与ABC[6]、DE[22]、IEDA[23]、IDE[23]和FOA[20]进行比较,其中,IEDA、DE、ABC和FOA的评价次数为18 000,IDE的评价次数为200。所有算法均独立运行10次,实验结果的误差如表16所示。 表16 基于实例4的算法结果误差 对于实例5,将ITPX-IAGA与GA[8]和DA[8]进行比较,其中,GA和DA的评价次数为300,且只有一次仿真结果,实验结果的误差如表17所示。 表17 基于实例5的算法结果误差 由表13可以发现,GA、DE和IDE均无法找到已知最优解,ABC和FOA在δARE和δWRE的误差均不为0,ITPX-IAGA的各种误差指标均为0,算法性能最优。表14中,GA和EDA均无法找到已知最优解,GSA在δBRE和δWRE的误差均不为0,ITPX-IAGA在10次实验中均找到已知最优解。表15中,PBIL和IEDA均无法找到最优解,而IDE、FOA和ITPX-IAGA均在10次实验中找到最优解。如表16所示,DE无法找到已知最优解,IEDA、IDE和FOA虽然可以找到已知最优解,但δARE和δWRE的误差均不为0,ABC和ITPX-IAGA在10次实验中均可找到最优解;比较可得ITPX-IAGA优于ABC。表17中,GA、DA、ITPX-IAGA的δBRE分别为26.13、15.31和0;ITPX-IAGA的δWRE为2.70,优于GA和DA的δBRE;ITPX-IAGA的δARE仅为1.26,可见ITPX-IAGA平均收敛性较好,其在求解较大规模的HFSP-UPM上具有很大优势。 3.4.2随机算例测试 TPX-IAGA与ITPX-IAGA的区别只有交叉算子不同,且交叉算子均满足2.3.9节的计算复杂度。实验的比较结果如表18所示,其中,tav为20次实验独立运行的平均时间。由表18可以发现,在Cbest的取值上,ITPX-IAGA可获得15个较优解,TPX-IAGA只获得8个较优解;在Cavg的取值上,ITPX-IAGA有17个较优解,TPX-IAGA只有1个较优解;在Cworst的取值上,ITPX-IAGA有14个较优解,TPX-IAGA只有8个较优解;在tav的取值,及各项指标的平均值(AVG),ITPX-IAGA的求解性能均优于TPX-IAGA。 表18 中大规模随机算例下算法的结果 为更好表明ITPX-IAGA对TPX-IAGA的优势,引入优越度这一概念,其公式为 PXY=(Y-X)/Y (18) 式中,PXY为变量X相较于变量Y的优越度。 本文中,X、Y分别为ITPX-IAGA和TPX-IAGA相同指标的求解结果。基于各算法的求解结果和优化时间等指标,计算相应的PXY,得出箱型图(图12、图13),其中,AVG表示本图中各指标(Cbest、Cavg、Cworst和tav)均值的优越度。由图12可知,ITPX-IAGA在4个解的性能指标上均有一定优势;由图13可知,ITPX-IAGA在tav等指标上具有较大优越性,其可缩短40%以上的优化时间。由此可以得出,ITPX-IAGA可在节省大量优化时间的基础上,提高ITPX算法的优化性能。综上所述,ITPX-IAGA在解决HFSP-UPM上具有良好的优化效果。 图12 ITPX-IAGA解的优越度箱型图 图13 ITPX-IAGA 平均优化时间的优越度箱型图 本文针对TPX随机取点方式存在的不足,提出一种改进TPX,即利用ITPX的精确取点方式提高算法的搜索效率和中后期的开发能力。为提高GA的求解性能,将激素调节机制用于选择算子,利用自适应的选择概率增强GA的收敛能力;将IAGA与ITPX结合,提出一种基于ITPX的IAGA调度方法来求解不相关并行机的混合流水车间调度问题。ITPX和自适应选择概率对比实验证明了ITPX算子和基于激素调节的自适应选择概率能有效提高算法的求解性能。工程实例和随机算例验证了ITPX-IAGA的有效性,证明了ITPX算法既能缩短40%以上优化时间,又能提高算法的求解性能。ITPX与TPX的算法复杂性分析,以及ITPX-IAGA实验结果说明,ITPX在单次取点时,ITPX-IAGA具有优越性。 未来,ITPX-IAGA可以在以下方向上继续深入研究:①基于强化学习,寻找最具潜在价值的异点区间,以进一步节省优化时间,提高算法性能;②ITPX的应用范围受限于解的编码方式,因此结合其他形式的调度问题,分析ITPX在其他编码方法中的切入点,有利于扩展ITPX的应用场景;③探索局部搜索方法或其他操作算子与ITPX的结合,进一步加快算法收敛,提高解的质量。2.2 激素调节规律在GA参数中的应用
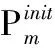
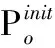
2.3 应用ITPX-IAGA求解HFSP-UPM

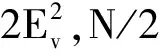
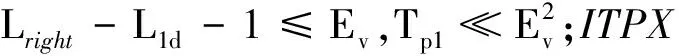
3 试验仿真与结果分析
3.1 实验设计
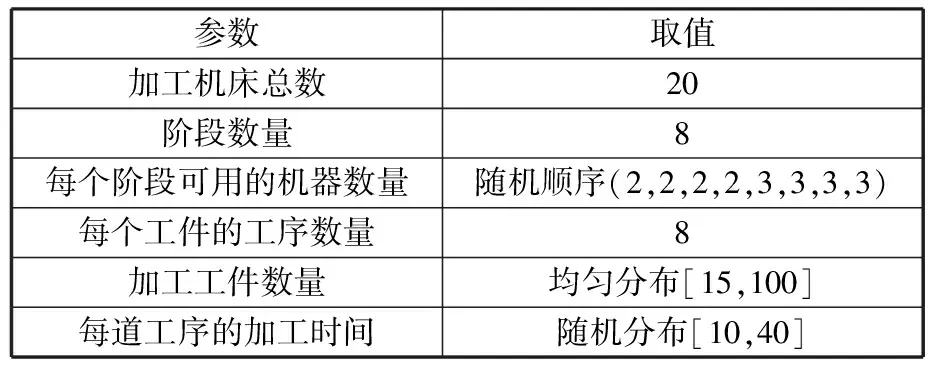
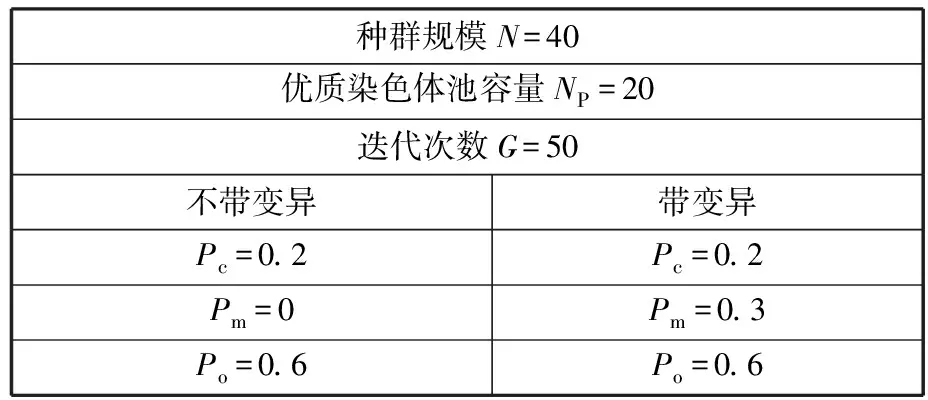


3.2 ITPX与TPX的对比实验
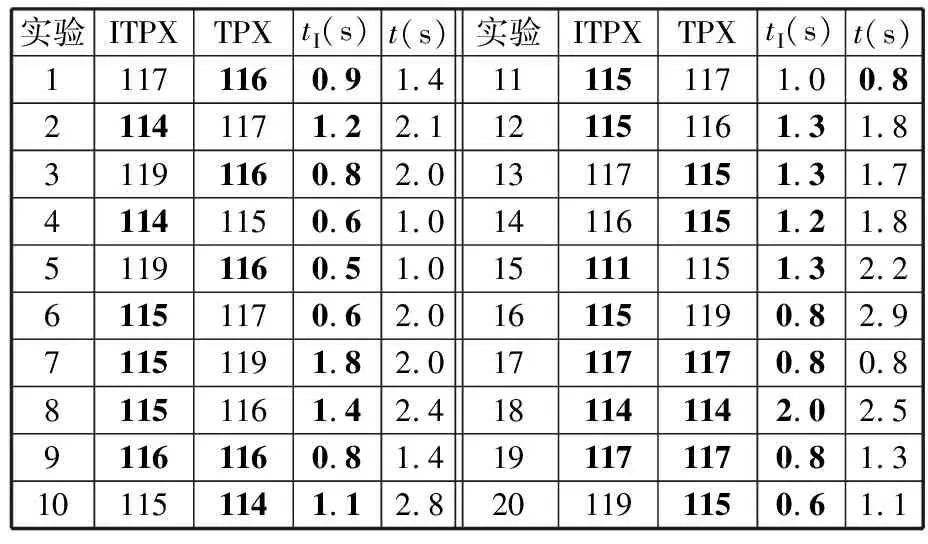
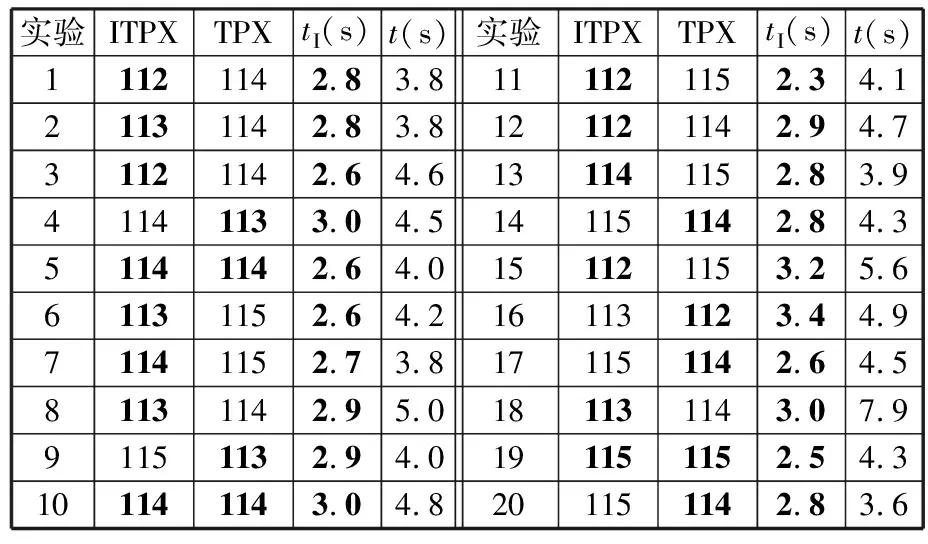
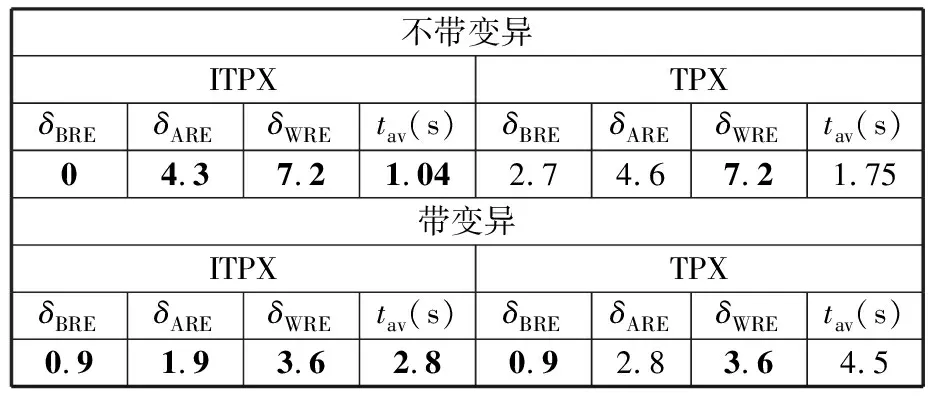
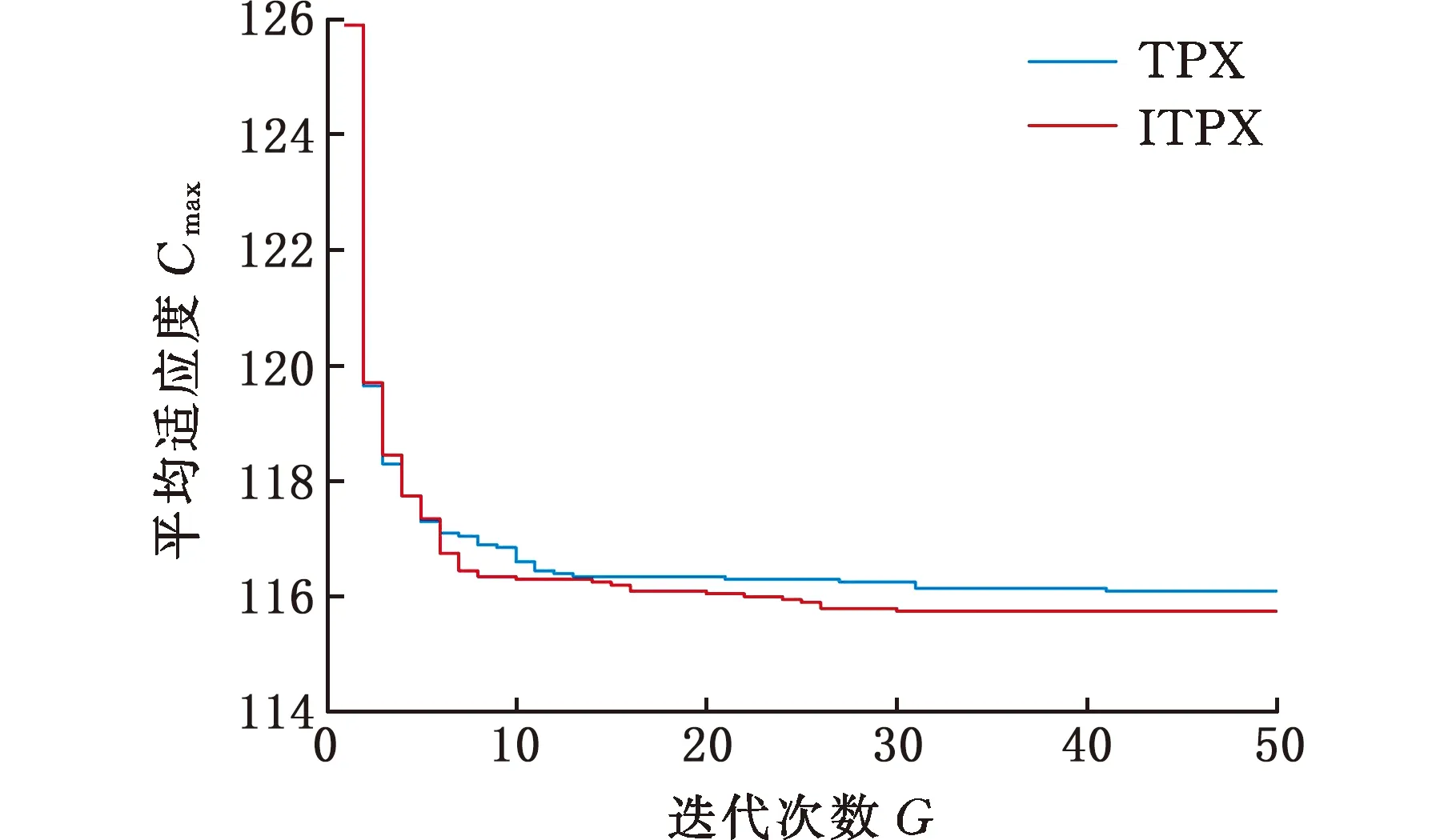
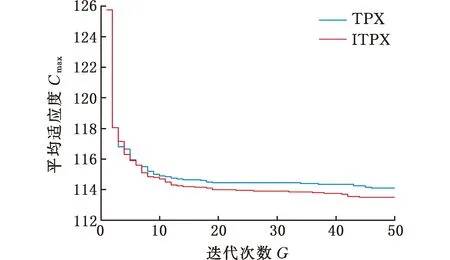
3.3 基于激素调节的自适应选择概率对比实验


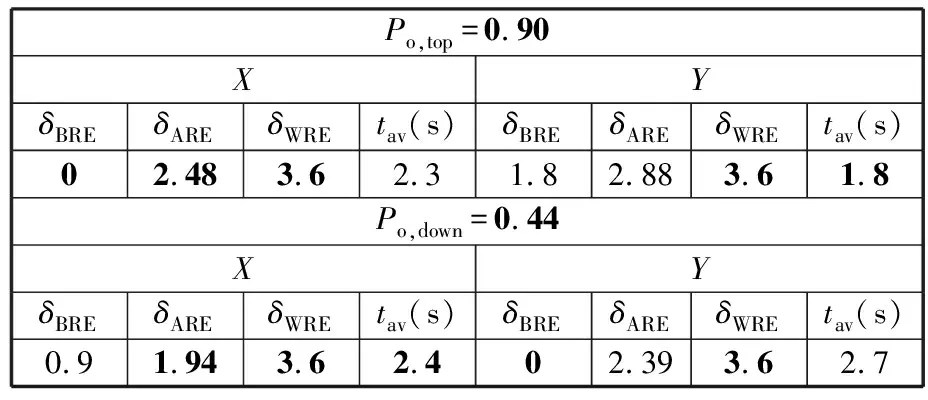
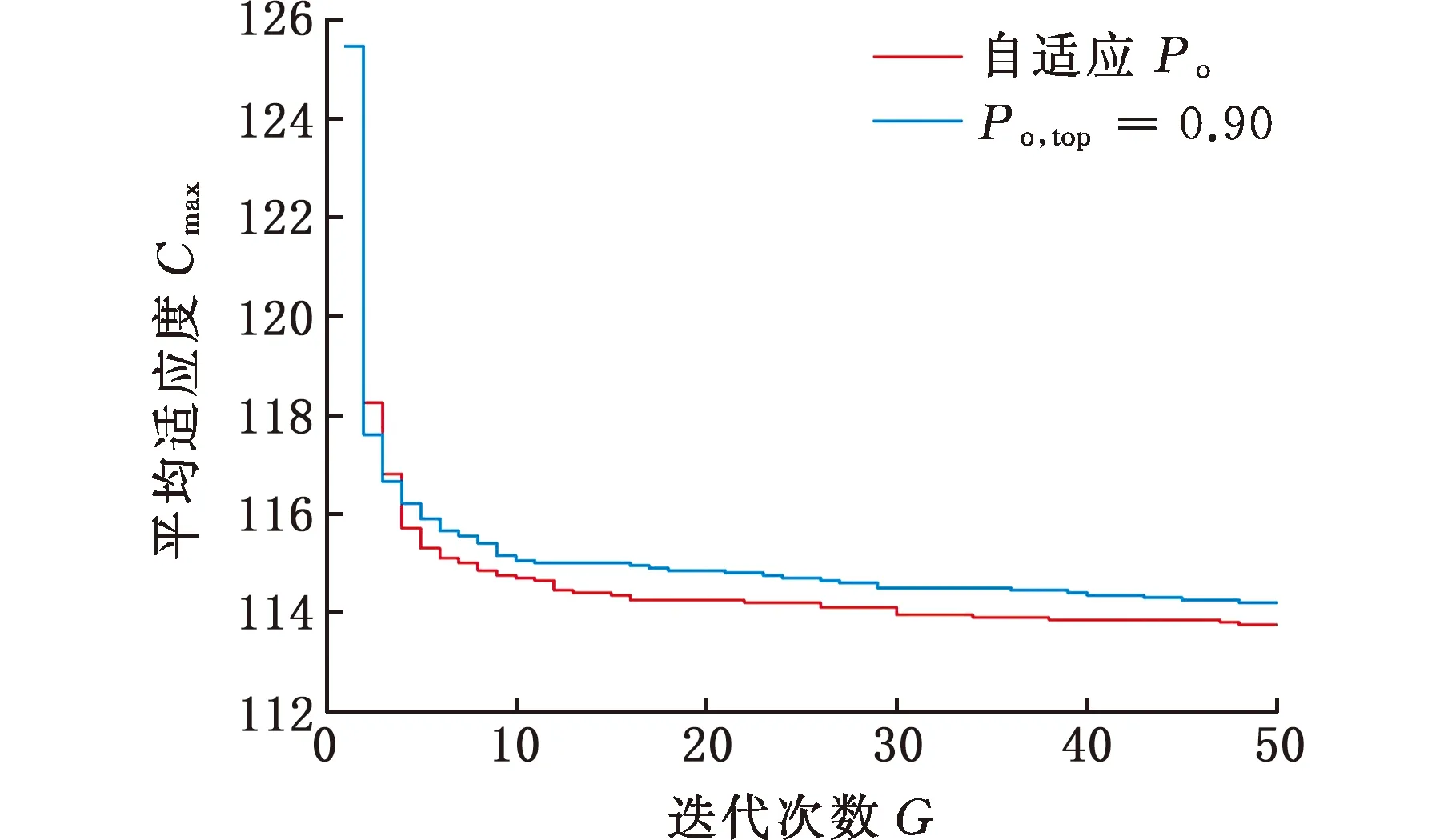

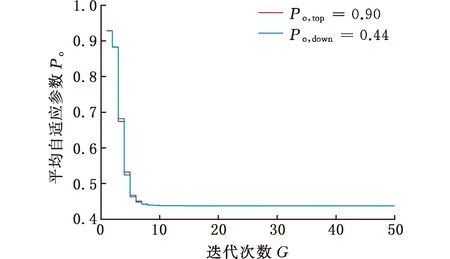
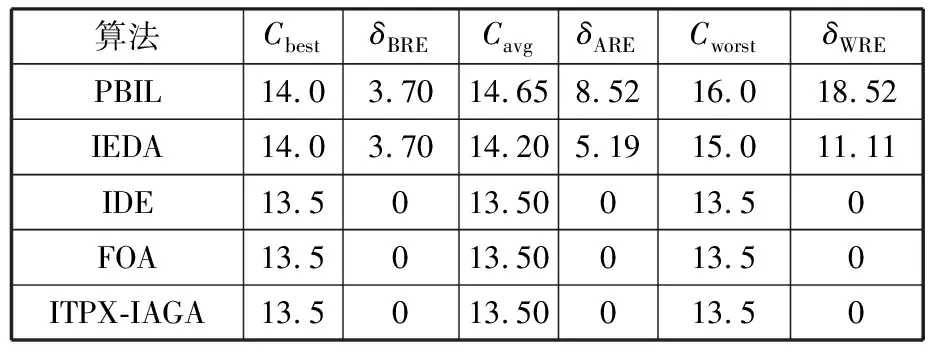
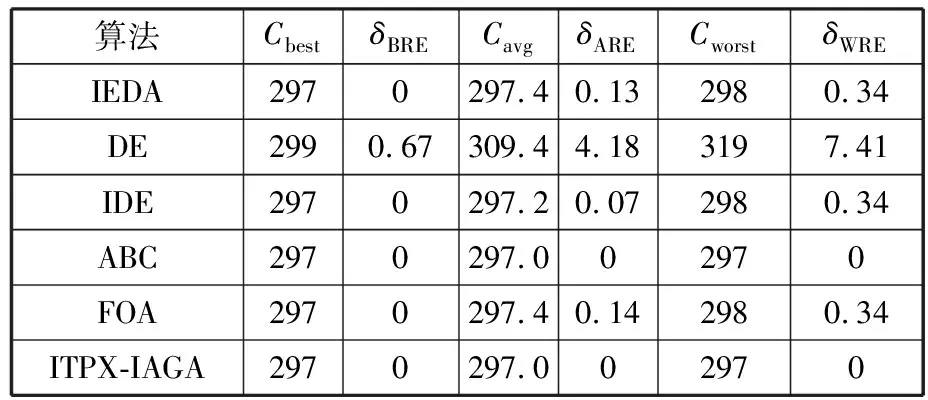
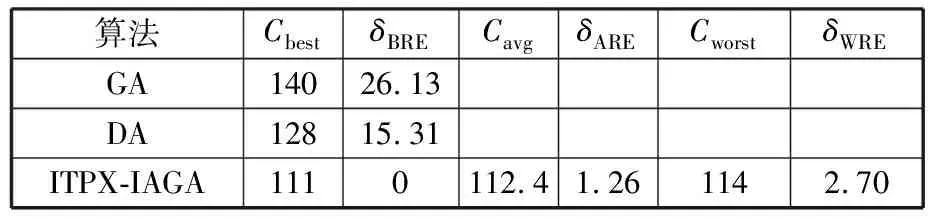
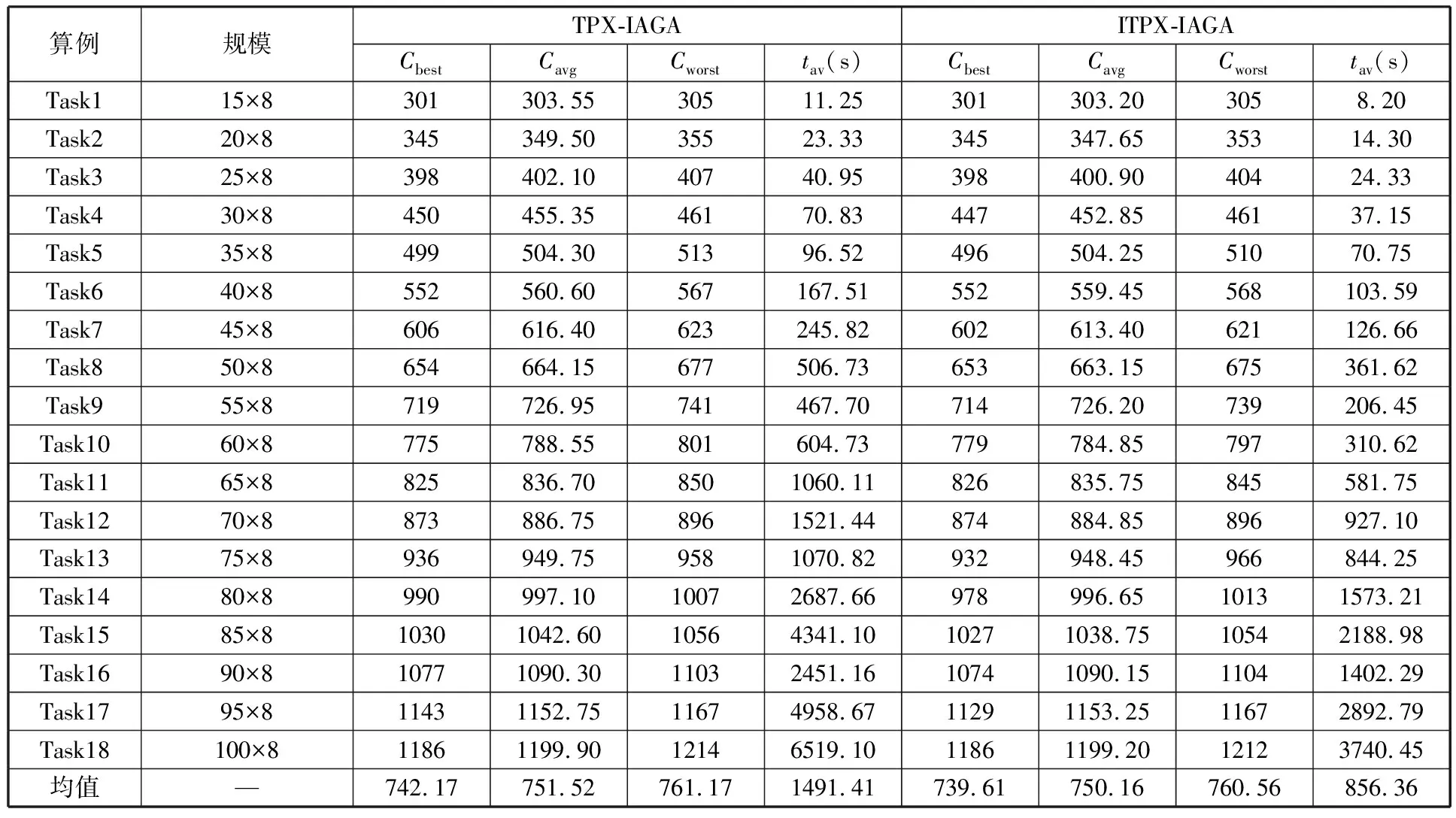
3.4 ITPX-IAGA实验
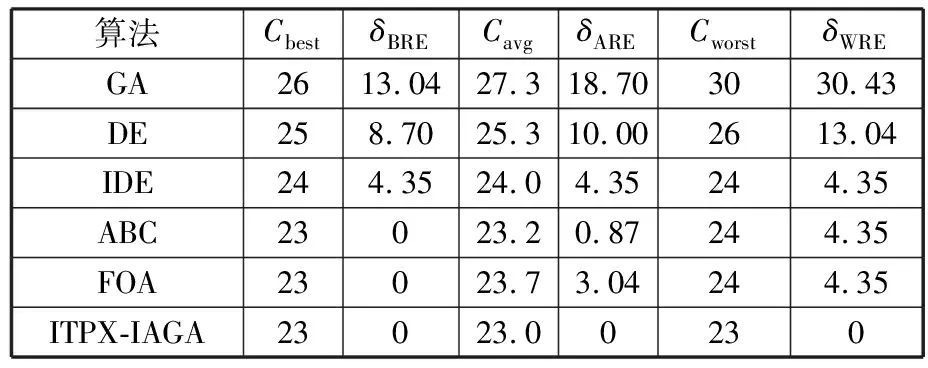
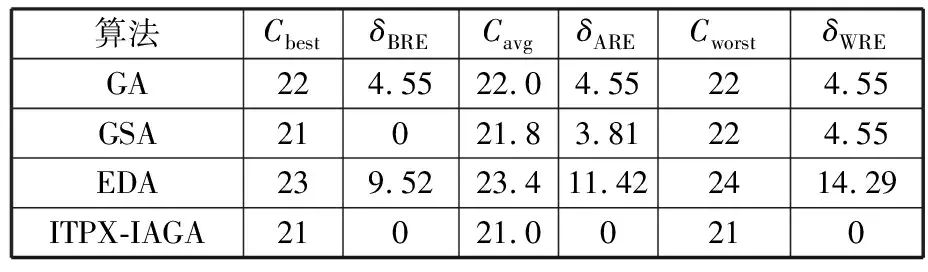
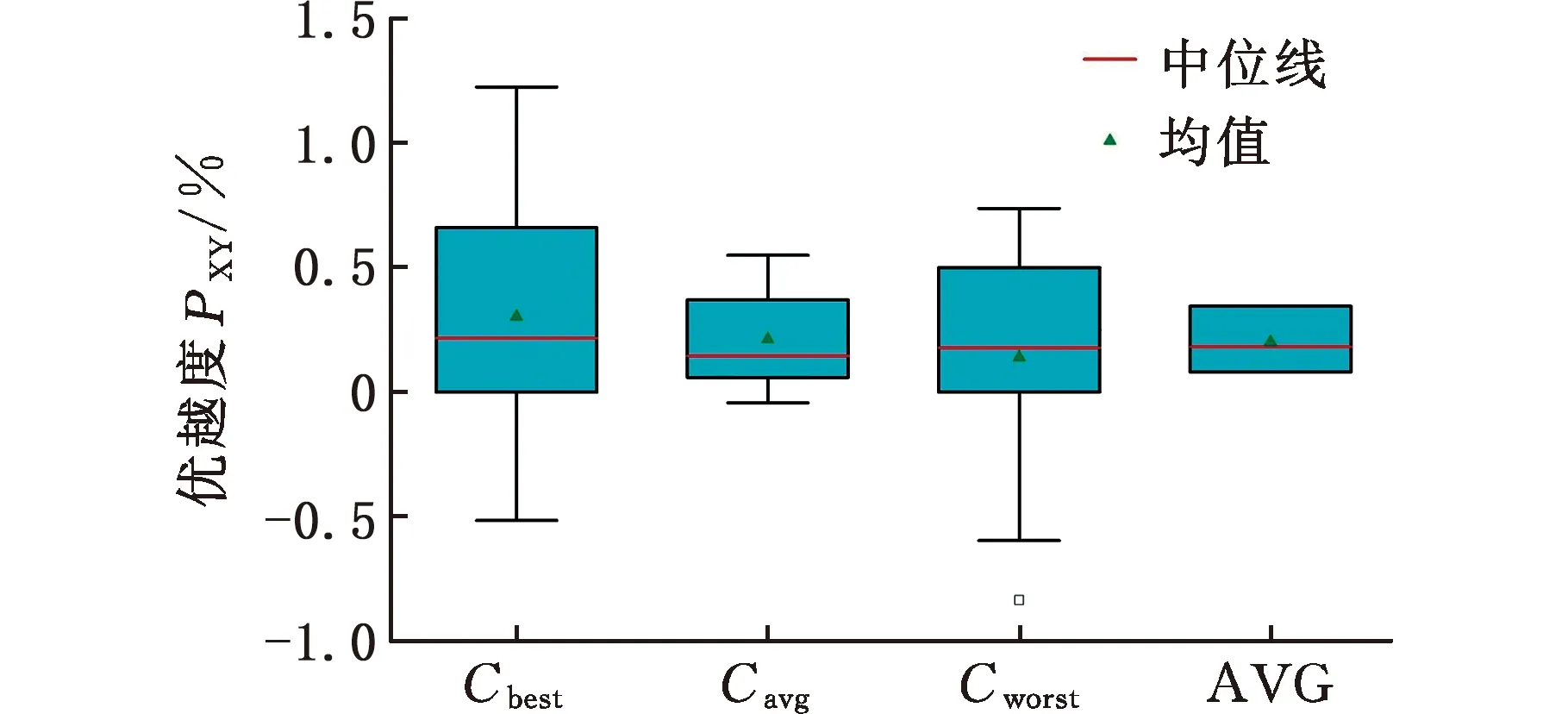
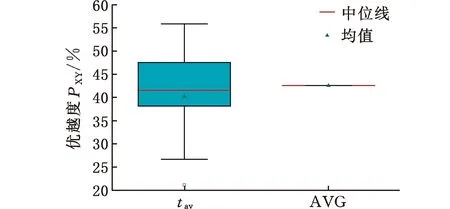
4 结论
