隧道施工对邻近桩基变形与受力影响数值模拟研究

姜梅杰,徐 涛,刘晓凤

(1.安徽建筑大学 土木工程学院,安徽 合肥 230601;2.安徽新基建有限公司,安徽 合肥 230001)

地铁是目前缓解交通拥堵的主要手段,但隧道开挖可能引起地面变形并影响相邻桩基,甚至造成邻近结构的破坏[1]。目前,国内外对隧道开挖下邻近桩基的影响已展开了一系列研究,如黄茂松等[2-4]基于Winkler地基模型,采用Euler-Bernoulli梁假设,推导了隧道开挖下桩基水平位移与竖向位移计算公式;沈建文等[5]以北京地铁10号线为背景,采用FLAC3D有限元软件,建立了既有桩基邻近盾构施工数值模型,在此基础上研究盾构施工全过程对桩基位移和地表沉降的影响;刘喆等[6]依托北京某地铁穿越工程,采用ANSYS有限元软件,研究盾构参数及施工加固措施对隧道开挖下邻近桥桩变形及受力的影响;王哲等[7]基于杭州地铁2号线,通过Advant Edge FEM有限元软件,研究盾构磨桩技术中刀具布置方式对桩基切削效果的影响;任磊等[8]以郑州某地铁工程为背景,采用FLAC3D有限元软件,建立三维数值模型,研究“土体注浆”“桩基承台加固”以及“注浆+承台加固”三种保护方案下桩基的变形规律;曾东洋等[9]依托哈尔滨地铁3号线,采用MIDAS-GTS三维有限元计算软件,建立三维数值模型,研究矿山法施工中超前加固措施对桩基变形的影响。

可以看出,以上研究是通过有限元软件基于具体案例展开分析,模拟结果往往也针对特定案例成立,对于类似案例的指导作用还存在一定限制。本文基于现有离心模型试验,采用有限元软件建立数值模型,通过与离心模型试验实测结果比较验证模型的合理性,在此基础上研究地层损失、土体黏聚力、桩隧距离、隧道轴线埋深以及隧道半径对隧道施工地层损失扰动下邻近桩基变形及受力的影响。

1 数值模拟

1.1 黏土地基数值模型

1.1.1 黏土地基离心模型试验

Loganathan等[10]开展了三组黏土地基下不同隧道轴线埋深的离心模型试验。模型地基长度650mm,宽度200mm,高度300mm;桩基轴线与隧道轴线的水平距离(下文简称桩隧距离)x=55mm,隧道轴线埋深H=150mm、180mm和210mm,隧道半径R=30mm,桩径D=9mm,桩基埋深L=180mm,试验模型率n=100,模型尺寸如图1所示。离心模型试验桩基采用铜管模拟,铜管外部涂有环氧树脂,外径为9mm,模型隧道内芯采用直径为54mm的铝管制作,其外部包裹橡胶模,内芯与橡胶模的空隙之间充满硅油后外径为60mm。试验过程中在100g离心加速度下通过伺服控制,将模型隧道橡胶模与铝管空隙内占总体积1%的硅油排出,模拟隧道施工引起的1%地层损失。

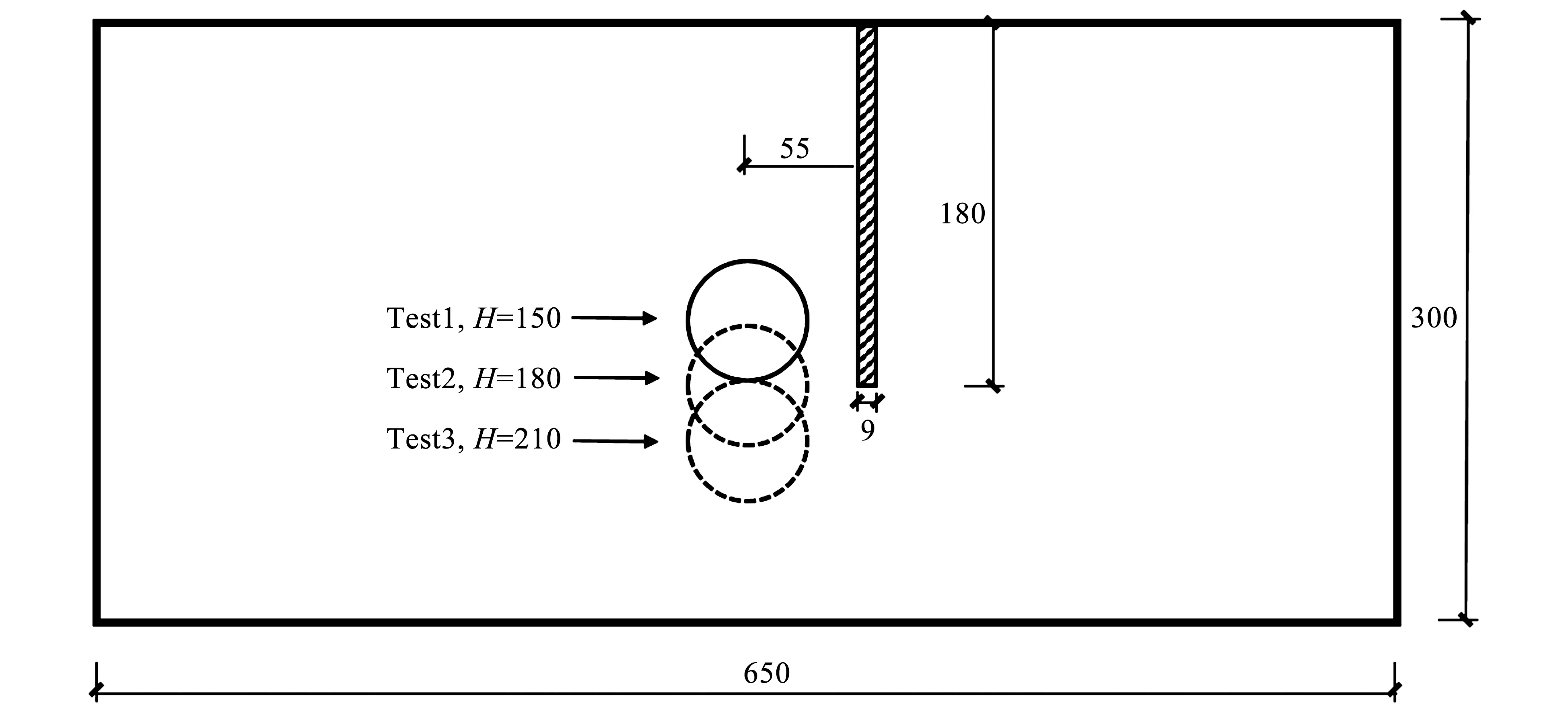
图1 黏土地基离心模型试验示意图(单位:mm)

1.1.2 数值模型

采用PLAXIS3D建立离心模型试验对应原型的三维数值模型。数值模型地基长度(x轴方向)为65m,宽度(y轴方向)为20m,高度(z轴方向)为30m,如图2所示。为便于建模与分析,地基土采用Mohr-Coulomb模型,表1概括了黏土地基材料参数[11]。

表1 黏土地基材料参数

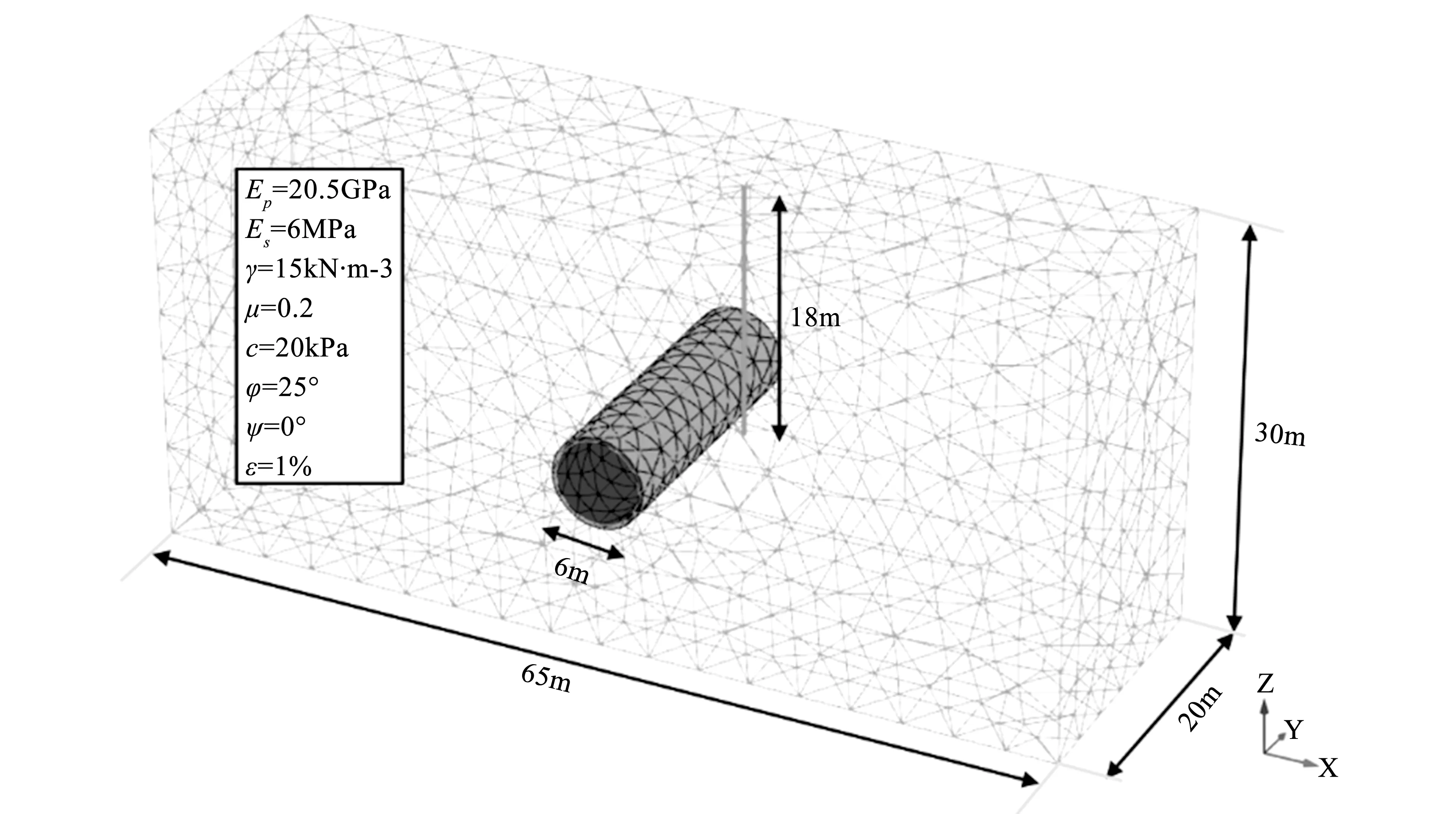
图2 黏土地基数值模型示意图

1.1.3 计算过程

隧道施工后管片通常坐落在下部土体,因而采用图3所示“同底圆”的地层损失模型更为合理[12]。数值模拟过程与离心模型试验相同,每一步计算至力学平衡和变形稳定[13]。具体如下:首先,通过“K0过程”生成地基自重应力;然后,激活相应梁单元和板单元;最终,为防止隧道与桩基的激活改变土体初始应力状态,先重置前置位移为零,通过停用相应土体单元且隧道的边界收缩按非均匀地层损失模型施加,模拟隧道的掘进过程,并记录桩身弯矩与水平位移。

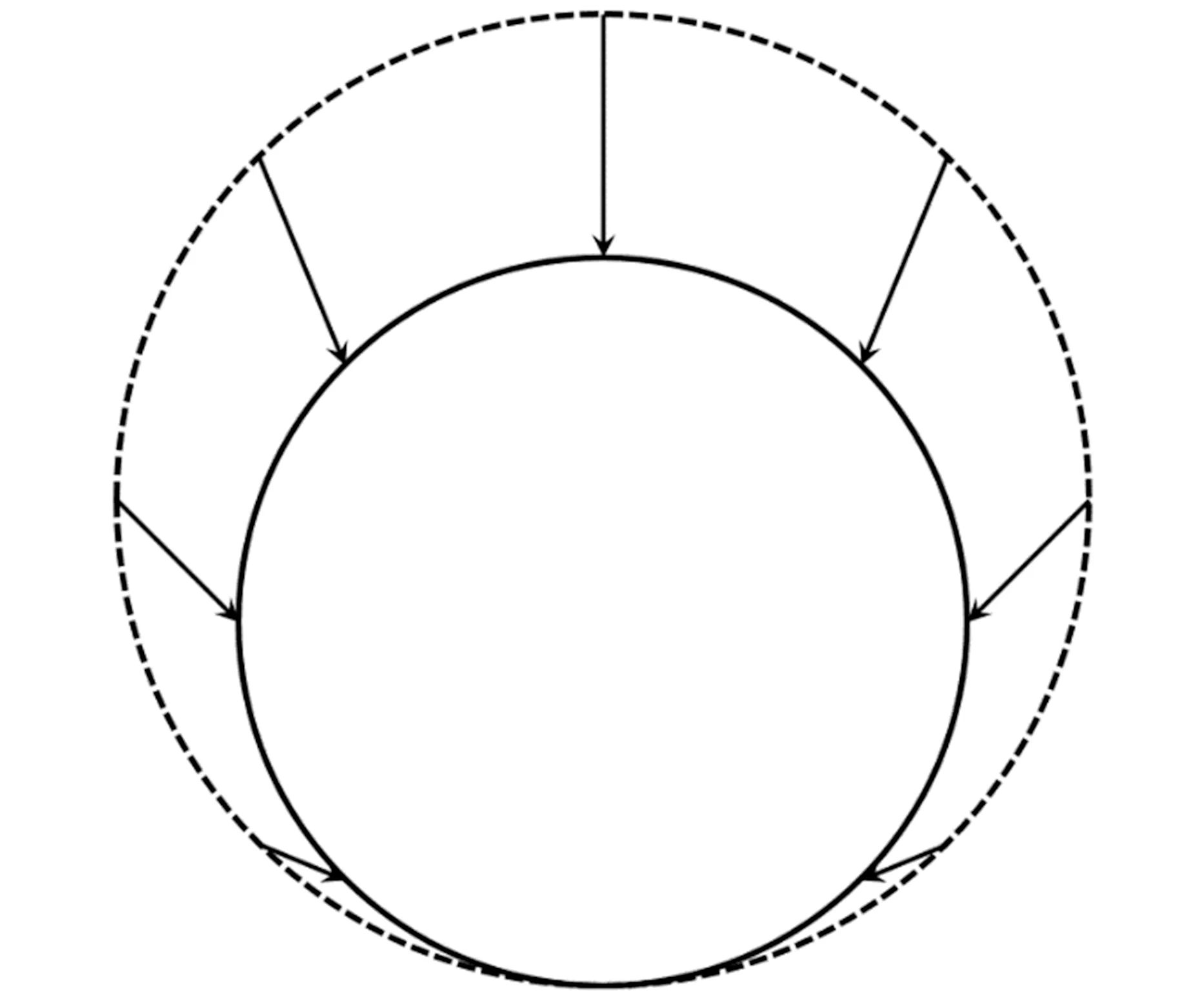
图3 非均匀地层损失模型

1.1.4 计算结果

图4给出了数值模拟计算结果与离心模型试验实测结果的对比,为进一步验证数值模型的可靠性,结果分析中还增加了与黄茂松理论解析的对比。在理论分析中黄茂松采用两阶段分析法,基于Winkler地基模型与Euler-Bernoulli梁假设,得出隧道开挖下邻近桩基位移计算公式,研究隧道施工对邻近桩基的影响[2-4]。为简化起见,下文涉及到采用这种方法作为理论解析解的,本文统称为“黄茂松法”。可以看出,数值模拟与离心模型试验以及“黄茂松法”计算结果基本吻合,说明本文数值模型结果是合理的。当隧道轴线埋深不大于桩基埋深时,由于隧道施工地层损失扰动下隧道轴线附近土体变形最大,因此桩身水平位移在隧道轴线处最大;当隧道轴线埋深大于桩基埋深时,桩底周围土体变形最大,因此桩身水平位移在桩身底部最大。

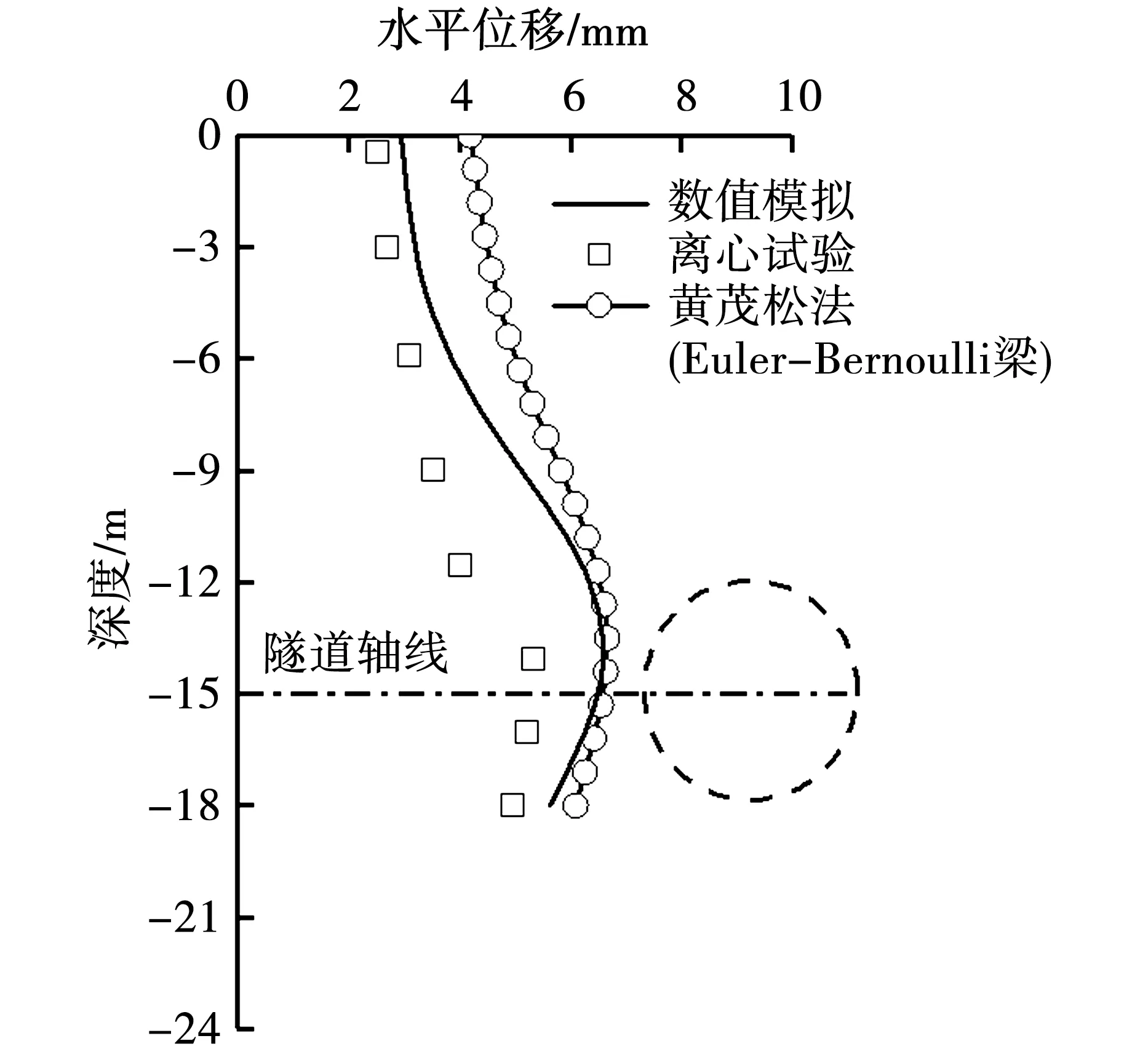
(a)H=15m

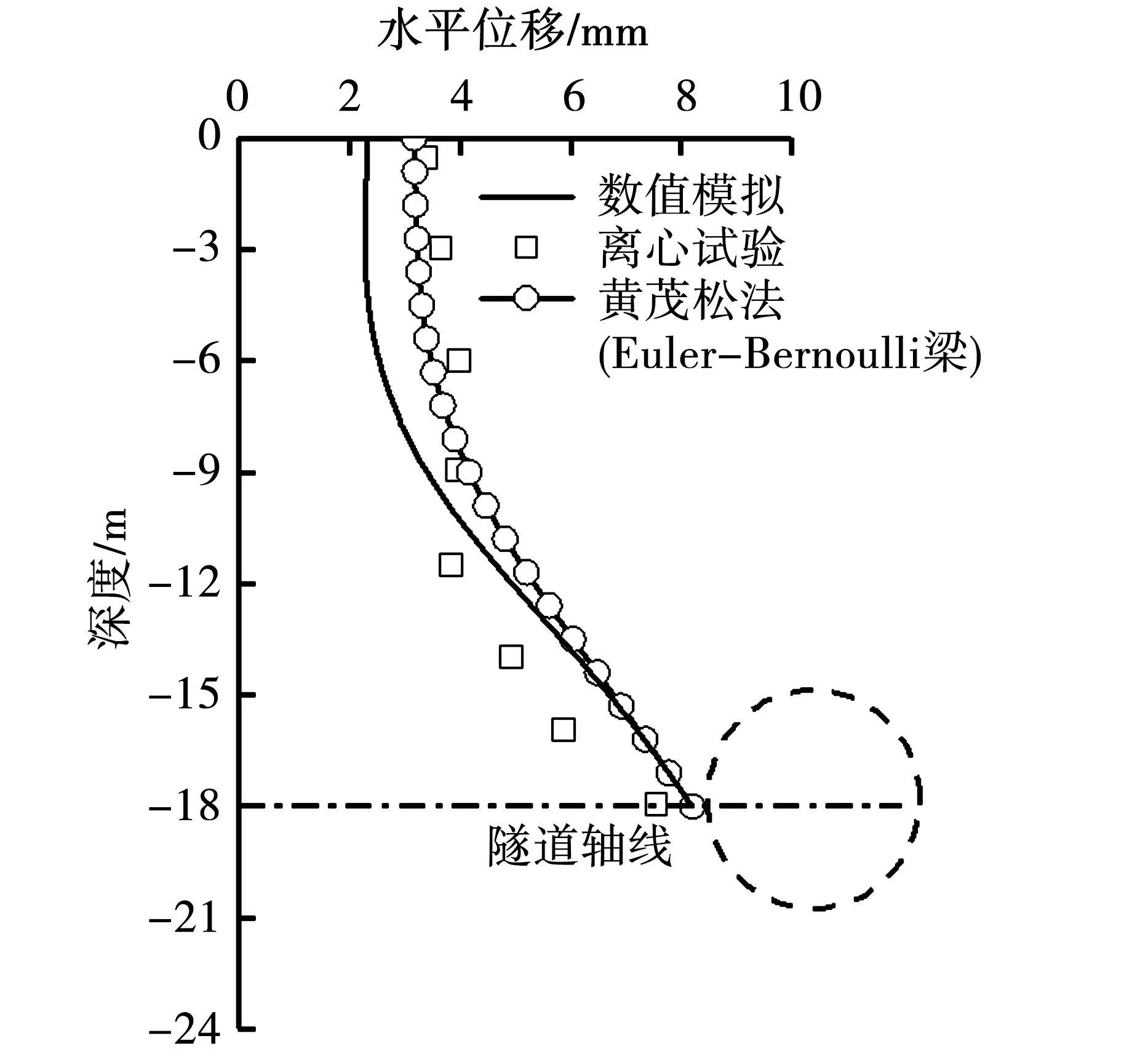
(b)H=18m

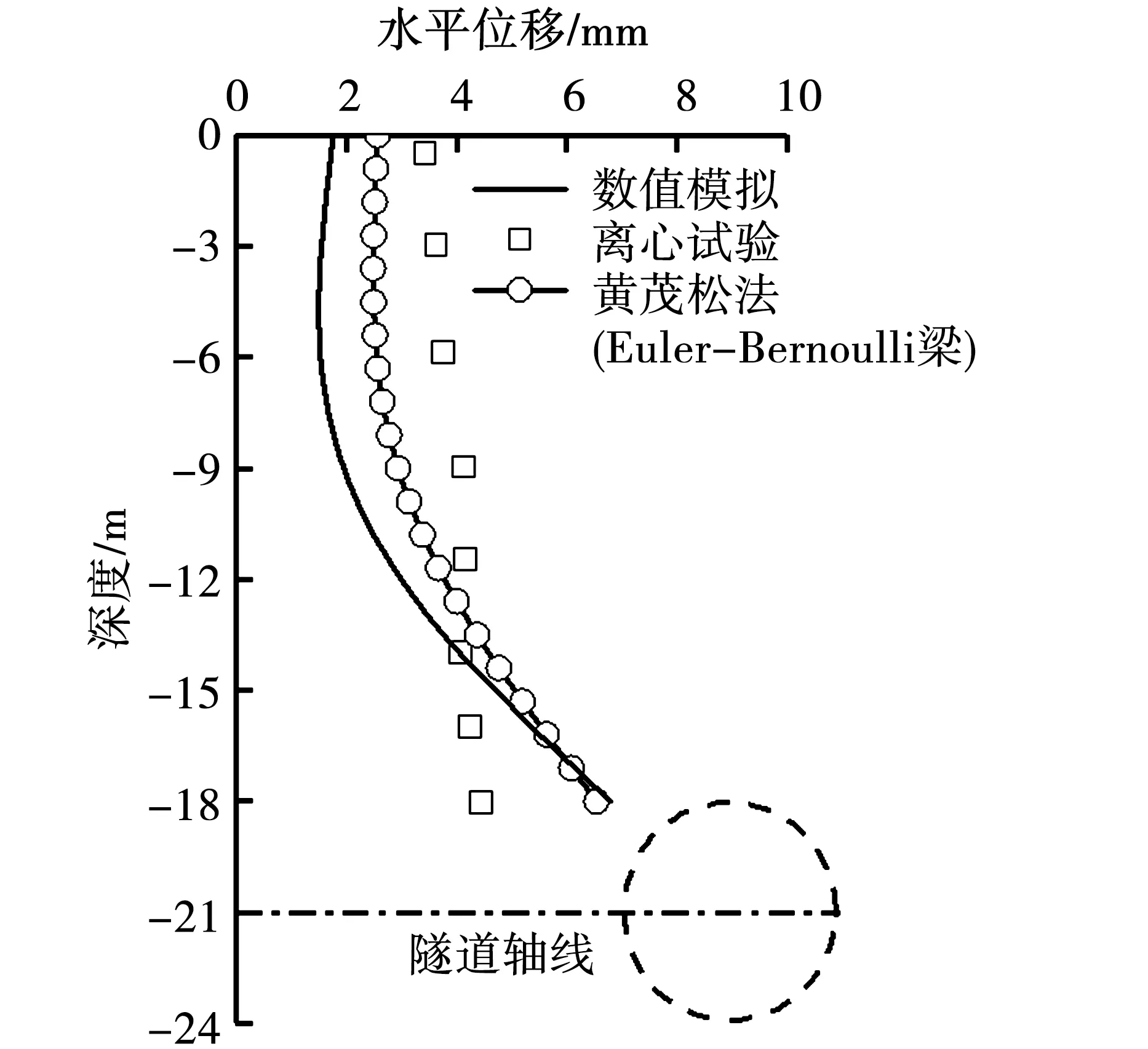
(c)H=21m图4 不同隧道轴线埋深下桩身水平位移对比曲线

1.2 砂土地基数值模型

1.2.1 砂土地基离心模型试验

Ng等[14]进行了一系列离心模型试验,研究盾构施工对邻近桩基的影响。模型地基长度1246mm,宽度228mm,高度750mm,隧道半径R=76mm,桩基埋深L=490mm,桩径D=20mm,桩隧距离x=114mm,试验模型率n=40,模型尺寸如图5所示。离心模型试验地基采用丰浦砂制备,桩基采用外径为20mm的铝管模拟,隧道采用内部充水的圆柱形橡胶袋模拟。试验过程中在100g离心加速度下通过伺服控制,将模型隧道橡胶袋内占总体积1%的水排出,模拟隧道施工引起的1%地层损失。

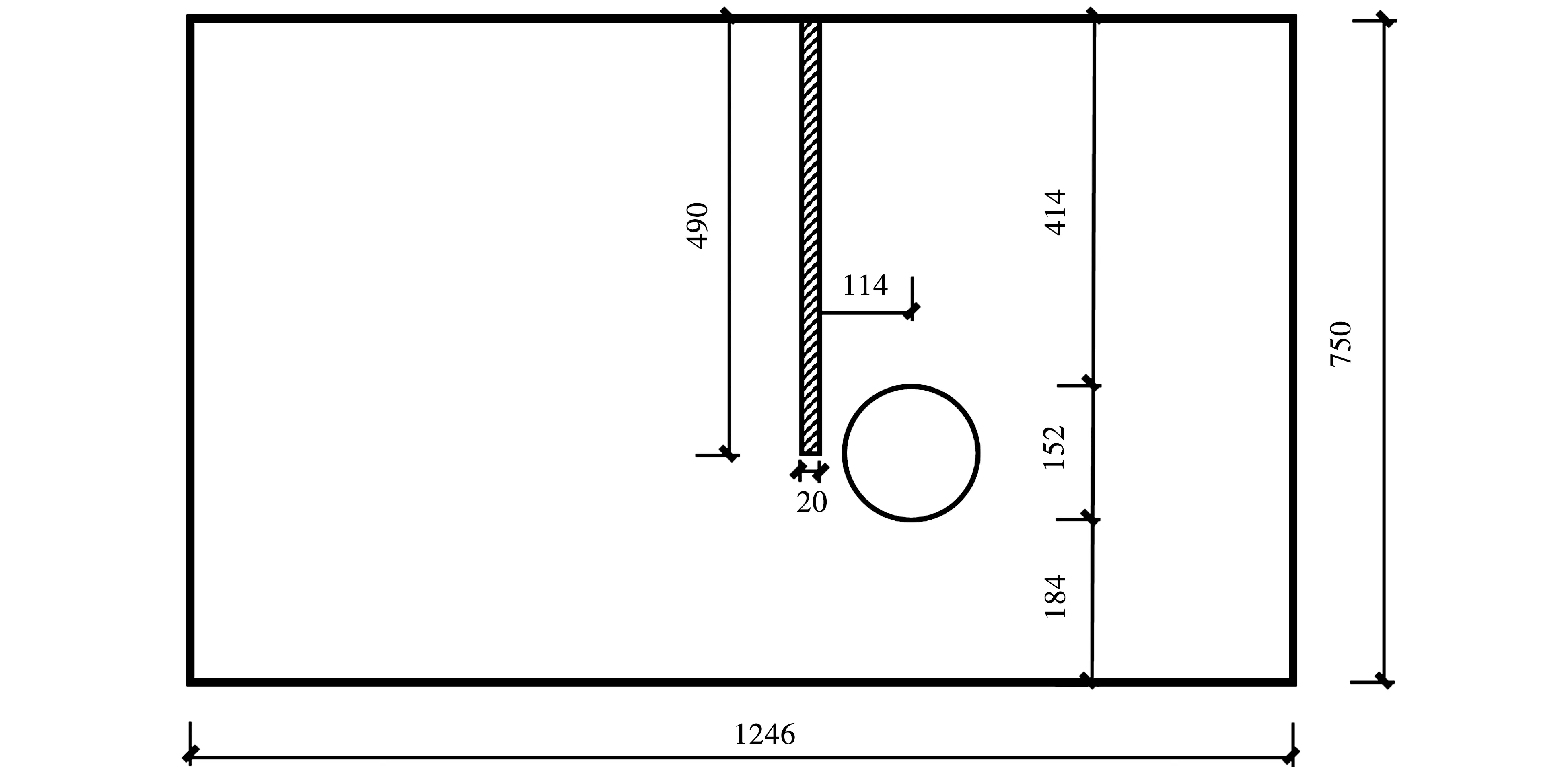
图5 砂土地基离心模型试验示意图(单位:mm)

1.2.2 数值模型

采用PLAXIS3D建立离心模型试验对应原型的三维数值模型。数值模型地基长度(x轴方向)为49.84m,宽度(y轴方向)为9.12m,高度(z轴方向)为30m,如图6所示,表2概括了砂土地基材料参数[14]。

表2 砂土地基材料参数

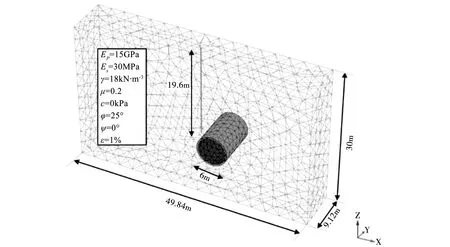
图6 砂土地基数值模型示意图

1.2.3 计算过程

本节数值计算过程与Loganathan等[10]离心试验的数值计算过程相同不再赘述,图7给出了数值模拟计算结果与离心模型试验实测结果以及“黄茂松法”计算结果的对比。可以看出,数值模拟与离心模型试验以及“黄茂松法”计算结果基本吻合,说明本文数值模型结果是合理的。

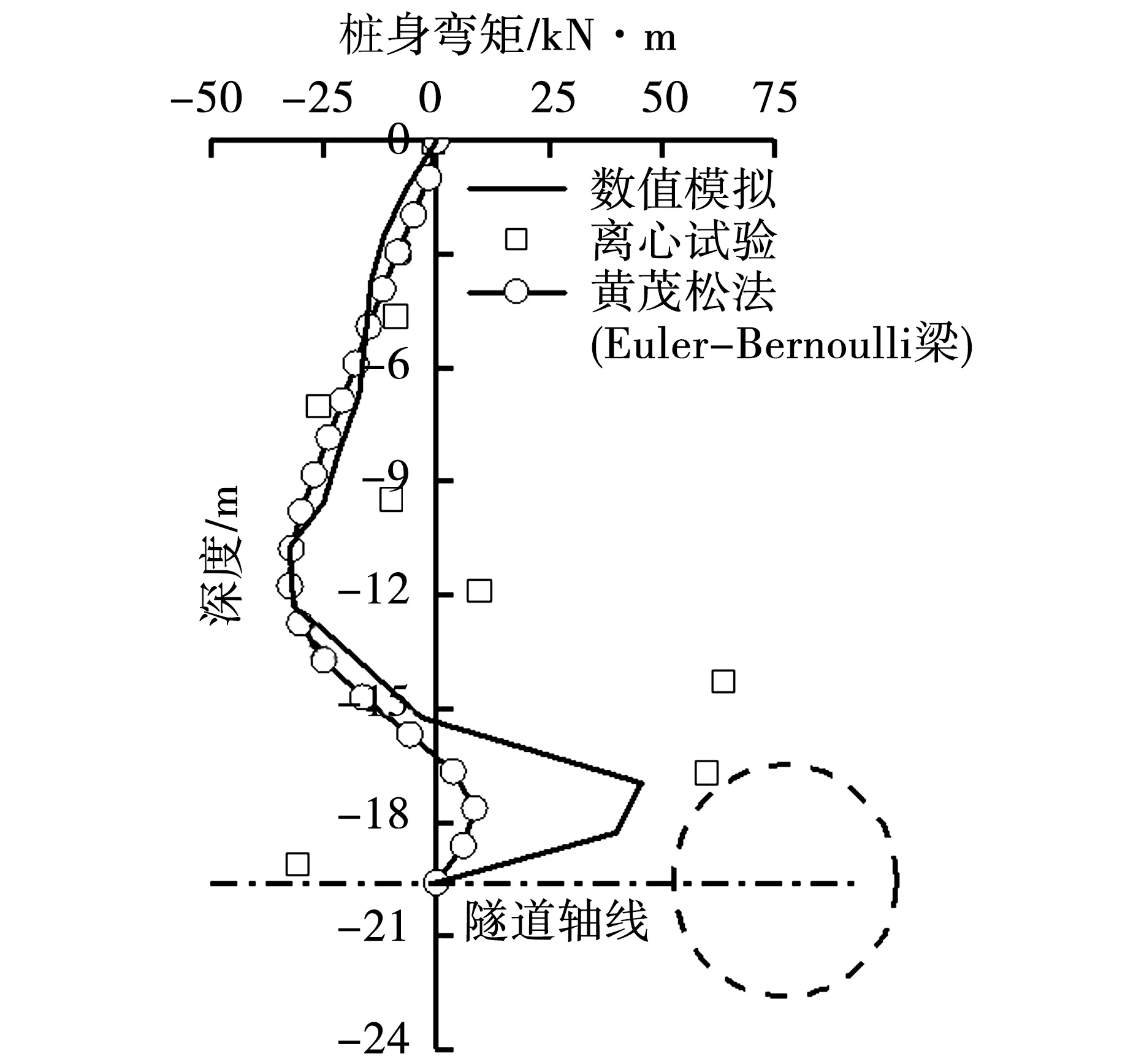
图7 桩身弯矩对比曲线

2 参数分析

这里分析地层损失、土体黏聚力、桩隧距离、隧道轴线埋深以及隧道半径对桩基变形及受力的影响。在研究每个因素参数对桩基的影响时,仅改变该因素,其余参数保持不变。参数如下:隧道半径R=3m,隧道轴线埋深H=18m,桩隧距离x=5.5m,桩径D=1.0m,桩基埋深L=18m,桩基弹性模量Ep=20GPa,土体重度γ=15kN/m3,弹性模量Es=6MPa,泊松比μ=0.2,黏聚力c=20kN/m2,内摩擦角φ=20°,地层损失ε=1%。

2.1 隧道轴线埋深

这里研究隧道轴线埋深对桩基变形及受力的影响,分别计算隧道轴线埋深H=15m、18m和21m等三种情况下桩身水平位移与弯矩分布,对应的隧道轴线埋深与桩基埋深比值H/L分别为0.8、1.0和1.2。

图8给出了不同隧道轴线埋深对隧道施工地层损失扰动下桩身水平位移及弯矩分布曲线。桩身水平位移为正表示桩基朝向隧道变形;桩身弯矩为正表示桩体朝向隧道弯曲。可以看出,当H/L为0.8此时桩基埋深大于隧道轴线埋深,桩身水平位移沿桩基埋深先增大后减小,最大值出现在隧道轴线处;桩身上部弯矩为正,下部为负,且桩身最大弯矩为负,位于隧道周围。当H/L为1.0此时桩基埋深与隧道轴线埋深相等,桩身水平位移沿桩基埋深逐渐增大,桩底出现最大水平位移;桩身弯矩沿桩基埋深基本先增大后减小,最大值出现在桩身中部。当H/L为1.2,此时桩基埋深小于隧道轴线埋深,桩身水平位移和弯矩分布与H/L为1.0时相似。

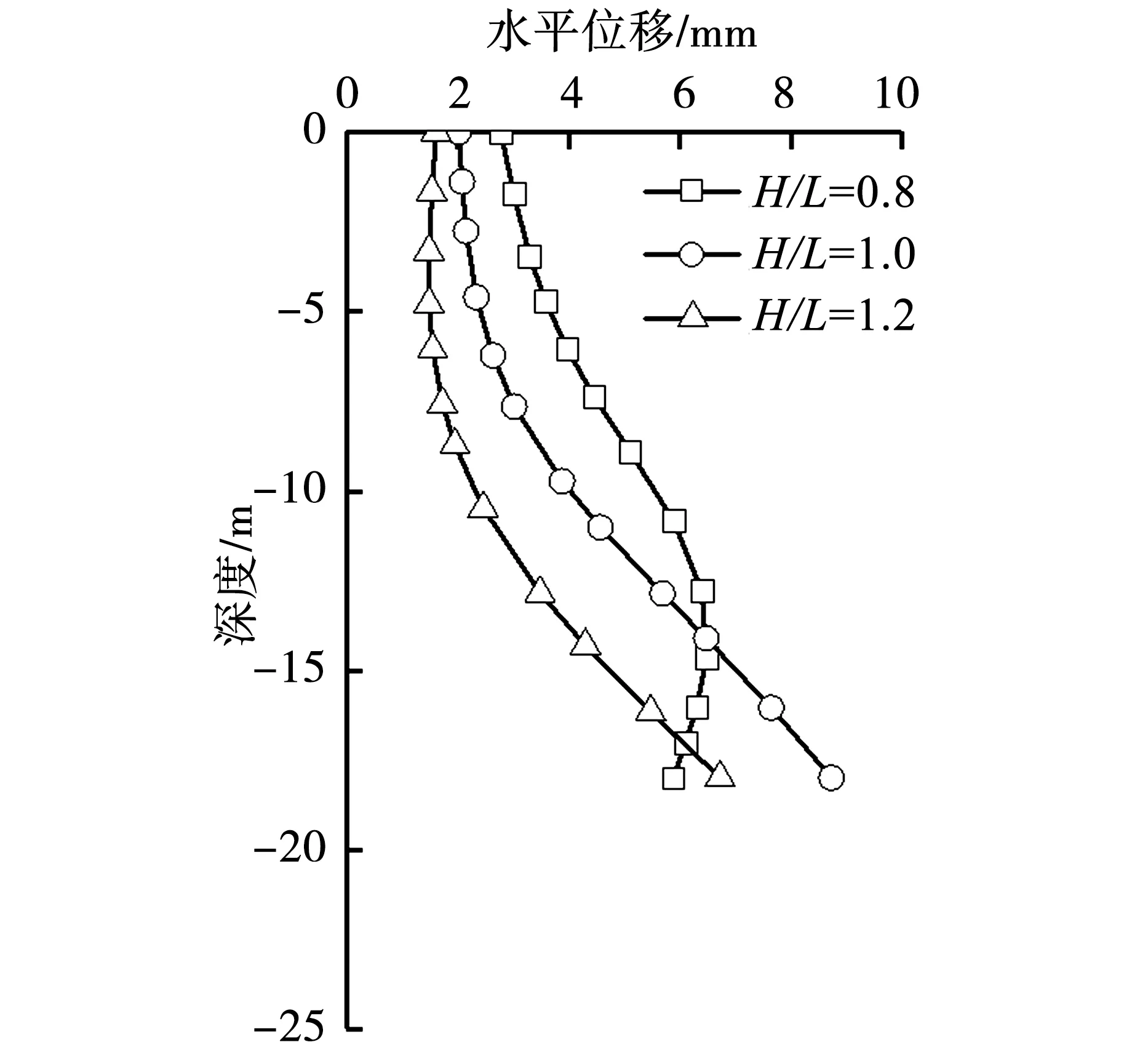
(a)桩身水平位移对比曲线

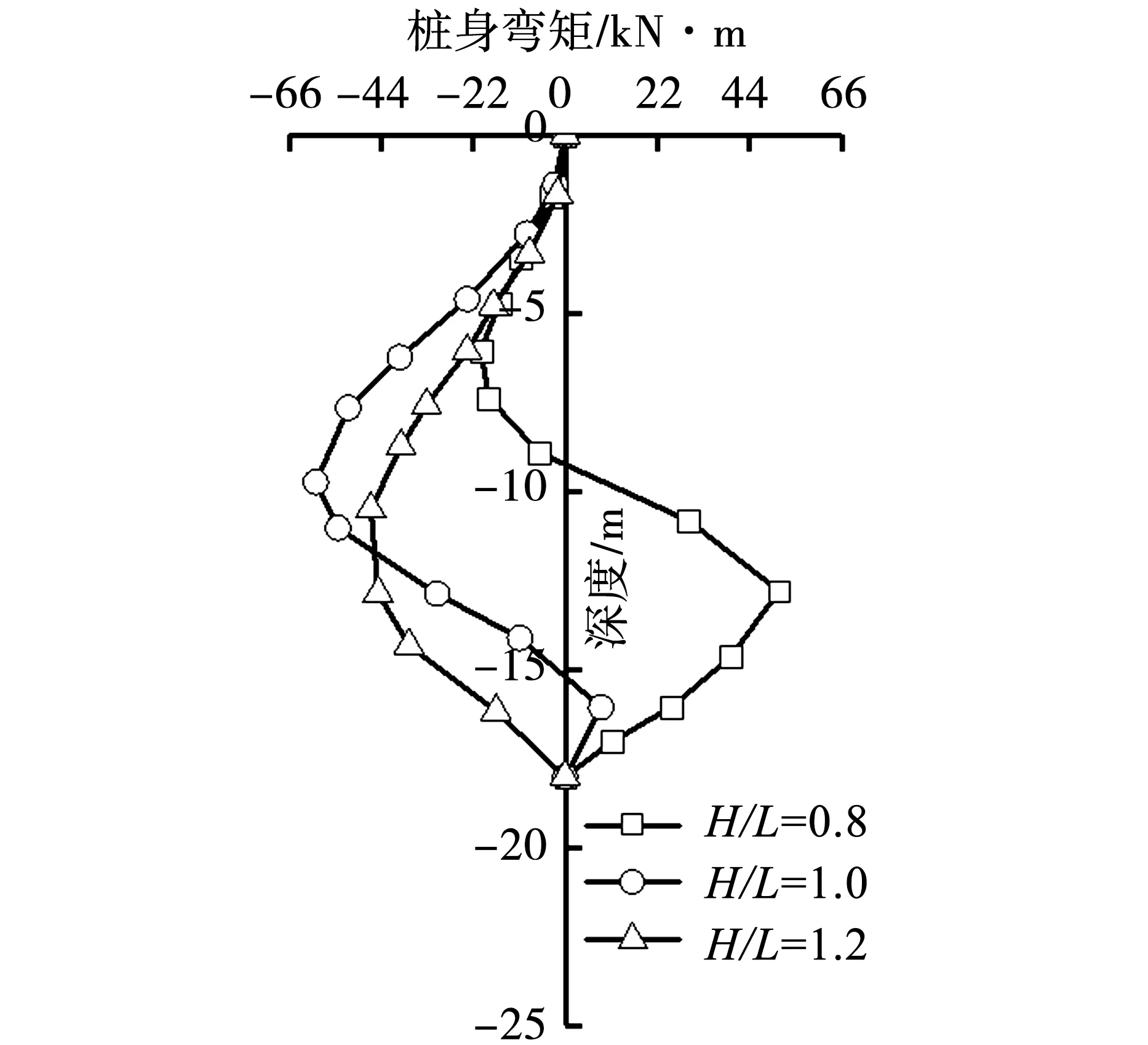
(b)桩身弯矩对比曲线图8 隧道轴线埋深对邻近桩基水平位移及弯矩的影响

当隧道轴线埋深与桩基埋深比值H/L=0.8、1.0和1.2时,隧道施工地层损失扰动下桩基最大水平位移分别为6.5mm、8.7mm和6.7mm,最大弯矩分别为51.1kN·m、59.5kN·m及46.4kN·m,即当桩基埋深与隧道轴线埋深相等时,桩身最大水平位移和弯矩值达到最大。

2.2 桩隧距离

这里研究桩隧距离对桩基变形及受力的影响,分别计算桩隧距离x=6m、9m、12m、15m和18m等五种情况下桩身水平位移与弯矩分布,对应的桩隧距离与隧道半径比值x/R分别为2、3、4、5和6。

图9给出了不同桩隧距离下桩身水平位移及弯矩分布曲线。可以看出,随着桩隧距离增加桩端水平位移降低,当桩隧距离与隧道半径x/R≥4时桩身水平位移趋于均匀,桩身中部的桩身最大弯矩显著降低。

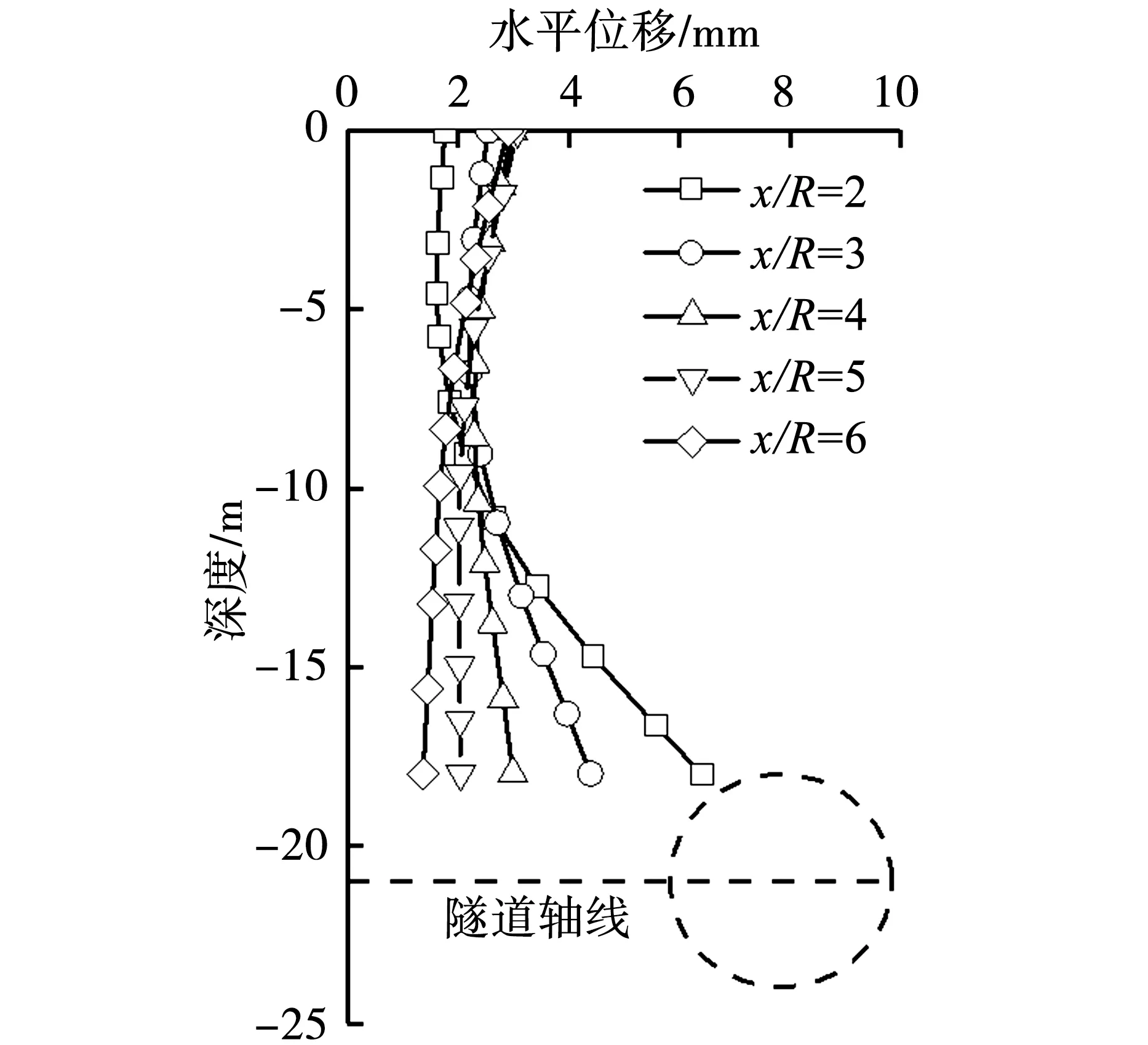
(a)桩身水平位移对比曲线

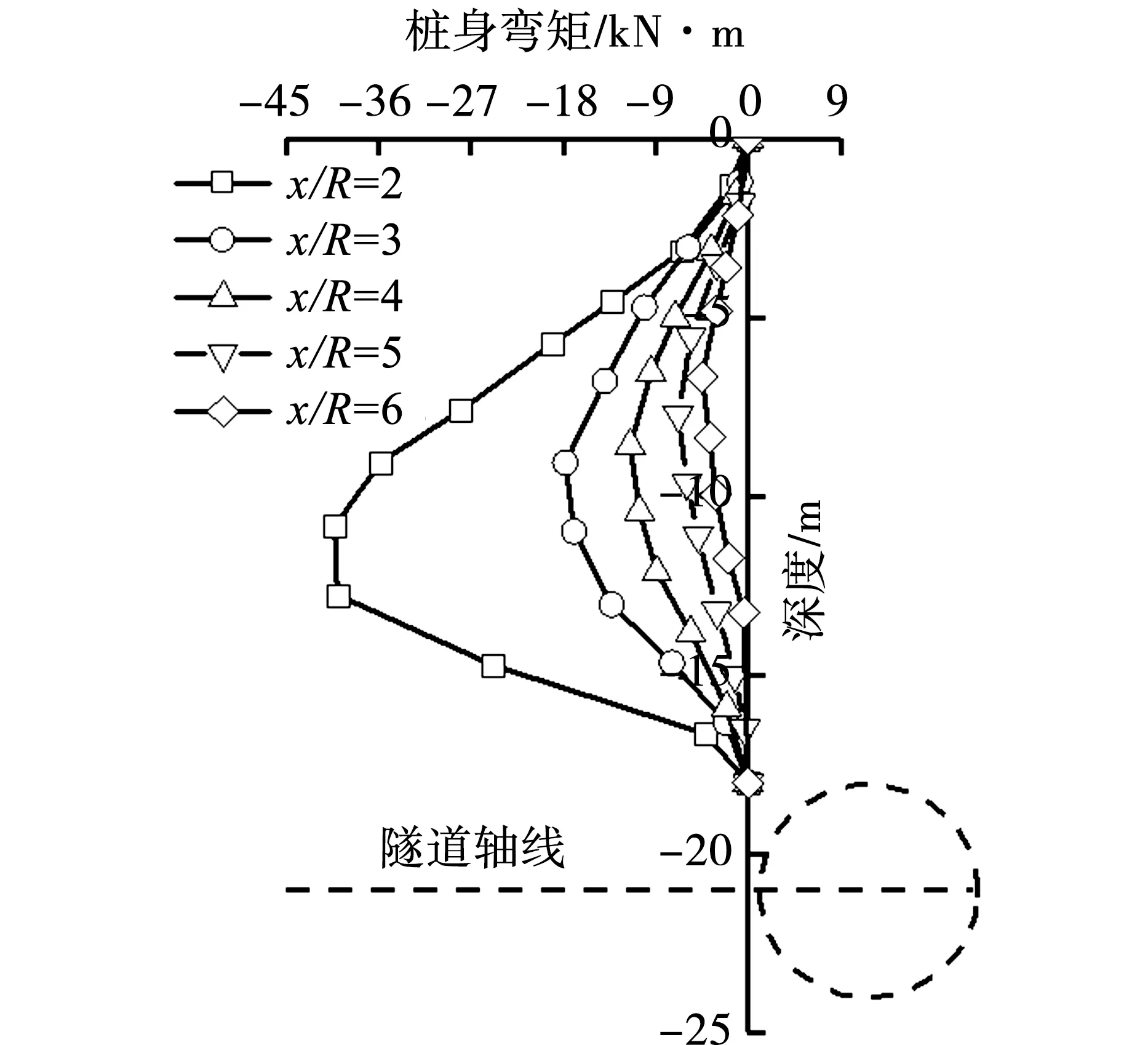
(b)桩身弯矩对比曲线图9 桩隧距离对邻近桩基水平位移及弯矩的影响

图10给出了不同桩隧距离下,桩基最大水平位移和最大弯矩变化曲线,当桩隧距离与隧道半径比值x/R=2、3、4、5、和6时,隧道施工地层损失扰动下桩基最大水平位移分别为6.4mm、4.4mm、3.0mm、3.0mm和2.9mm;最大弯矩分别为40.3kN·m、17.8kN·m、11.5kN·m、6.8kN·m和4.5kN·m。可以看出,当桩基轴线距离隧道轴线越远,桩基最大位移和最大弯矩就越小,当x/R≥4时,桩隧距离对桩身水平位移和弯矩影响不大。

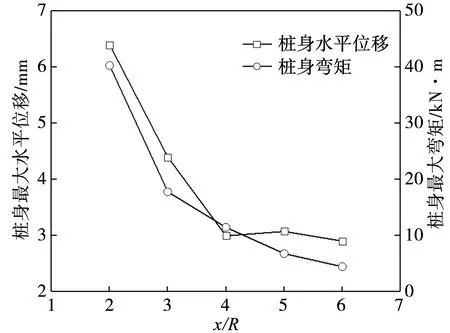
图10 桩基最大水平位移及弯矩变化曲线

2.3 隧道半径

这里研究隧道半径对桩基变形及受力的影响,分别计算隧道半径R=2.0m、2.5m和3.0m等三种情况下桩身水平位移与弯矩分布,对应的隧道半径与桩径比值R/D分别为2.0、2.5和3.0。

图11给出了不同隧道半径下桩身水平位移及弯矩分布曲线。可以看出,隧道半径对桩身水平位移与弯矩的分布模式影响不大。当隧道半径与桩径比值R/D=2.0、2.5和3.0时,隧道施工地层损失扰动下桩基最大水平位移分别为3.0mm、4.9mm和6.7mm;最大弯矩分别为26.1kN·m、36.8kN·m及46.4kN·m,即随着隧道半径增加桩身水平位移和弯矩显著增大。这是因为隧道半径的增大,加剧隧道施工对自由场土体的扰动程度,使得桩基周围土体水平位移增大,从而导致桩身水平位移与弯矩变大。

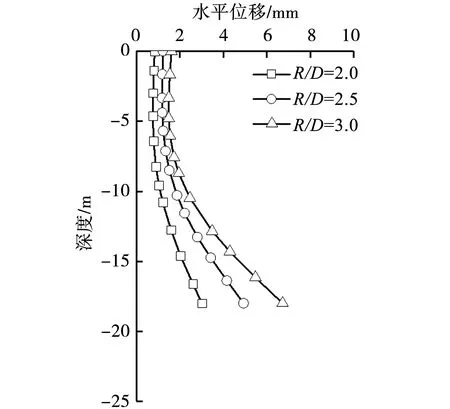
(a)桩身水平位移对比曲线

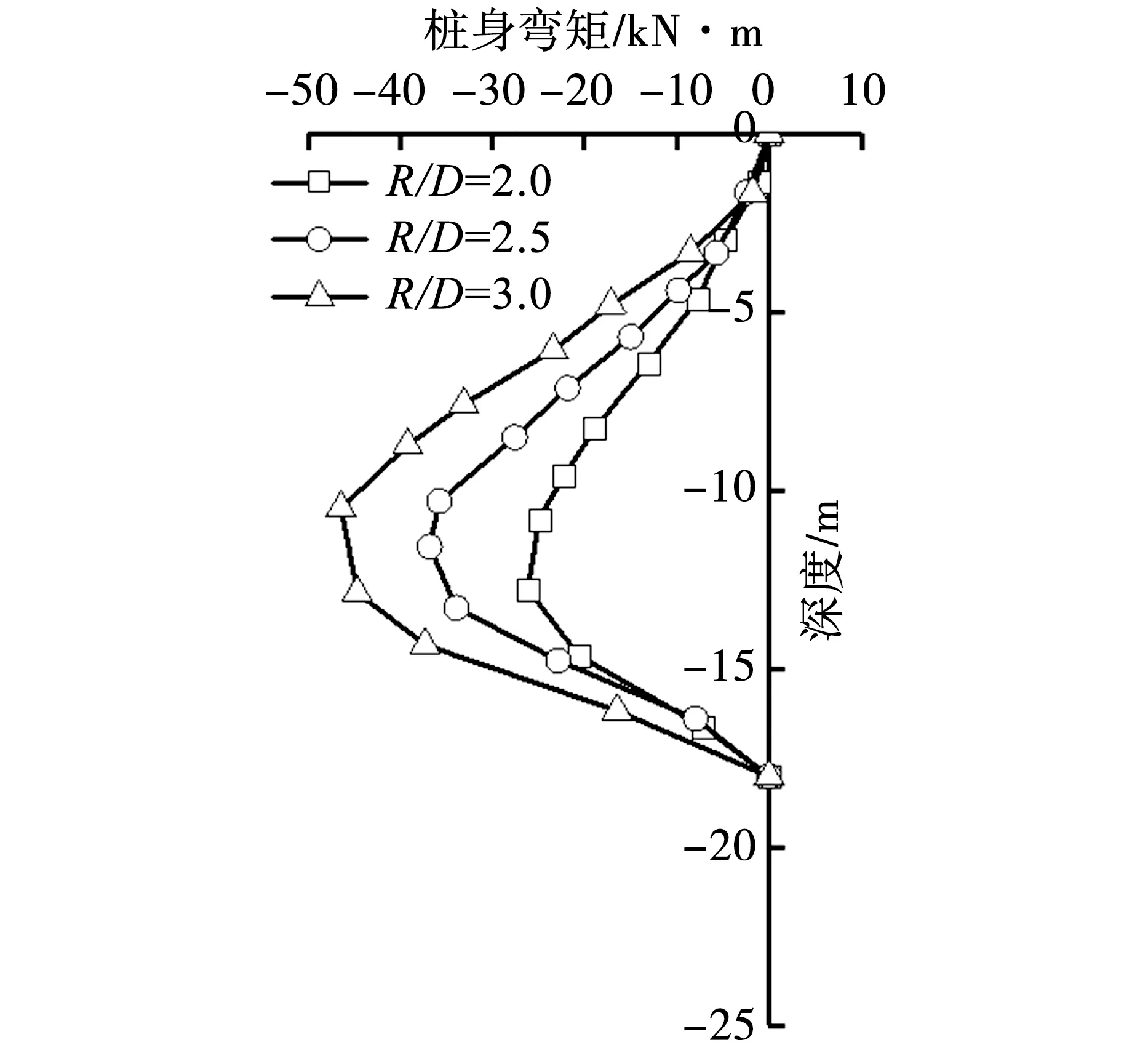
(b)桩身弯矩对比曲线图11 隧道半径对邻近桩基的影响

2.4 地层损失

这里研究地层损失对桩基变形及受力的影响,分别计算地层损失ε=1.0%、1.5%、2.0%、3.0%和5.0%等五种情况下桩身水平位移与弯矩分布。

图12给出了不同地层损失下桩身水平位移及弯矩分布曲线。可以看出,地层损失对桩身水平位移与弯矩的分布模式影响不大。当地层损失ε=1.0%时,隧道施工地层损失扰动下桩基最大水平位移为6.7mm,最大弯矩为46.4kN·m;当地层损失ε=5.0%时,桩基最大水平位移为14.0mm,最大弯矩为114.3kN·m。即随着地层损失的增大,桩身弯矩与桩身水平位移逐渐增大。这是因为地层损失的增大,加剧隧道施工对自由场土体的扰动程度,使得桩基周围土体水平位移增大,从而导致桩身水平位移与弯矩变大。

(a)桩身水平位移对比曲线

(b)桩身弯矩对比曲线图12 地层损失对邻近桩基水平位移及弯矩的影响

2.5 土体黏聚力

这里研究土体黏聚力对桩基变形及受力的影响,分别计算土体黏聚力c=20kN/m2、25kN/m2和30kN/m2等三种情况下桩身水平位移与弯矩分布。

图13给出了不同土体黏聚力下桩身水平位移及弯矩分布曲线。可以看出,当土体黏聚力c=20kN/m2、25kN/m2和30kN/m2时,隧道施工地层损失扰动下桩基最大水平位移分别为6.7mm、6.9mm和7.0mm;最大弯矩分别为46.4kN·m、48.3kN·m和49.2kN·m;即土体黏聚力对桩基水平位移和弯矩影响较小。

(a)桩身水平位移对比曲线

(b)桩身弯矩对比曲线图13 土体黏聚力对邻近桩基水平位移及弯矩的影响

3 结论

本文基于现有离心模型试验,采用有限元软件建立既有桩基邻近隧道施工数值模型,通过与离心模型试验实测结果比较验证数值模型的合理性,在此基础上研究地层损失、土体黏聚力、桩隧距离、隧道轴线埋深以及隧道半径对隧道施工地层损失扰动下邻近桩基变形及受力的影响,得出以下主要结论。

(1)当隧道轴线埋深与桩基埋深比值小于1时,隧道施工地层损失引起的桩身水平位移与弯矩最大值均位于隧道轴线处;当隧道轴线埋深与桩基埋深比值大于或等于1时,桩身水平位移最大值位于桩基底部,桩身弯矩最大值位于桩基中部。

(2)隧道开挖引起的桩身水平位移受土体黏聚力影响较小,但随隧道半径、地层损失的增加而增大,随桩隧距离的增大而减小;当桩隧距离与隧道半径比值大于4时,隧道开挖对桩身水平位移影响不大。

(3)隧道开挖引起的桩身弯矩受土体黏聚力影响较小,但随隧道半径、地层损失的增加而增大,随桩隧距离的增大而减小;当桩隧距离与隧道半径比值大于4时,隧道开挖对桩身弯矩影响不大。