基于GRA-IGA-BP的输电线路负荷预测

陈 静,蔡 金

(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)

近年来,由于电网的安全性以及稳定性变得尤为重要,因此有效且精准的输电线路负荷预测也是十分必要的。精准的输电线路负荷预测不仅可以确保电网稳定高效地运行,而且可以使我们对输电线路负荷需求做出更加准确的判断[1]。因此,对于输电线路负荷预测,国内外许多学者提出了不同的预测方案,邰能灵等人[2]提出了利用小波变换的预测方法,使用小波变换对不同序列的负荷数据进行预处理,然后将不同预测模型分析出的结果进行小波重构,最后获得一个完整的结果。蔡舒平等人[3]采用深度随机森林算法对用户负荷进行短期预测,并与支持向量机的回归算法、K近邻算法、贝叶斯岭回归算法、随机森林算法以及多个深度神经网络算法对比分析。陈振宇等人[4]提出了基于LSTM和XGBoost的组合模型,用于提升线路负荷的预测精度。邹品晶等人[5]提出在基于LSTM预测模型的基础上采用多变量进行输电线路负荷预测。虽然这些模型具有较好的时间序列处理效果,但是模型结构复杂,且训练时间长。

在神经网络的参数寻优方面,较为常用的寻优算法是遗传算法(Genetic Algorithm),刘春霞等人[6]提出了使用未改进的GA算法优化BP神经网络中重要参数的输电线路负荷预测模型,在使用传统的GA算法优化BP模型中的重要参数时[7],容易造成收敛速度慢,陷于局部最优,因此,本文利用改进过后的遗传算法(Improved Genetic Algorithm,IGA)搜索BP神经网络预测模型中重要参数权值和阈值的最优解,通过与BP神经网络模型,GA-BP神经网络模型做比较,本文所提出的模型能够有效地避免参数陷入局部最优问题,提高网络训练的收敛速度以及输电线路负荷预测精度。

1 基本原理

1.1 BP神经网络

在多种输电线路负荷预测模型中,由于BP神经网络的结构简单,故本文应用BP模型作为输电线路负荷预测模型。BP神经网络[8]是一种常见的人工神经网络,也称为反向传播神经网络。它是通常用于分类和回归等任务。BP神经网络通过误差的反馈来实现自己的学习过程,通过误差调整权值和阈值,以提高网络的准确性和泛化能力,而且在设定一个合理权值的条件下,具有一层隐藏节点的BP神经网络就可以从任意的n维映射到m维,BP神经网络的结构如图1所示。

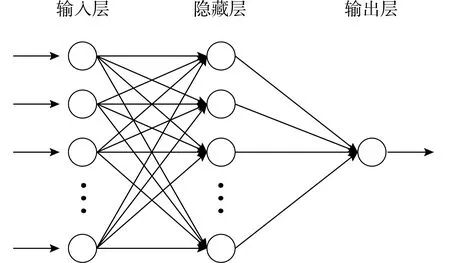
图1 BP神经网络拓扑结构

1.2 IGA算法

混沌映射是一类非线性动力学系统,其特点是具有混沌行为,即对初始条件的微小变化会导致系统演化出现极其不同的结果。混沌映射通常由一个简单的迭代公式描述,其迭代过程可以看作是一个动态系统的演化过程[9-10]。混沌映射的研究不仅有理论意义,还有实际应用价值。例如,混沌映射可以用于生成高质量的随机数序列,这对密码学和通信安全等领域非常重要。混沌映射的应用非常广泛,例如在密码学、图像压缩、随机数生成等领域都有重要的应用。本文选用Tent映射[11]用于生成遗传算法中分布均匀的混沌序列,数学表达式如式(1)所示。

(1)

式(1)中,p表示映射的次数,pi表示第i次映射的值。经过伯努利移位变换后的数学表达式如式(2)所示。

zk+1=(2zk)mod1

(2)

式(2)中,k表示映射的次数,zk表示第k次映射的值。

1.3 灰色关联分析

在研究不同影响因素之间的关联程度时,我们常采用灰色关联分析(Grey Relational Analysis, GRA)的方法,它可以用于分析多个因素对某一指标的影响程度,以及不同因素之间的相互影响关系。灰色关联分析的基本思想是将各个因素的数据序列进行标准化处理,然后计算它们与指标序列之间的关联度[12],从而确定各个因素对指标的影响程度。在计算关联度时,灰色关联分析采用灰色关联度函数,它可以有效地处理数据序列之间的不确定性和不完备性。本文采用以下步骤分析输电线路负荷的影响因素。

将输电线路负荷值设为参考序列,影响负荷的因素设为比较序列,y(k)为样本容量数,xi为特征量的个数。

(2)数据归一化

由于参考序列与比较序列在数量级和量纲上的不同,且为了更好地分析和预测,对设置好的序列做归一化处理。

(3)计算关联系数

设置比较序列与参考序列的关联程度,关联系数εi(k)如式(3)所示。

(3)

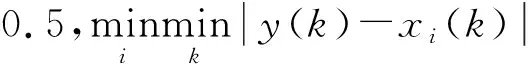
(4)确定关联度

教育生态学研究开始于20世纪80年代，它是将教育和生态环境联系在一起，并对其之间的相互关系及其机理进行研究。随着信息技术的发展，“互联网+教育”正以前所未有的速度冲击高等教育，一种新的高等教育生态系统正在形成[1]。在新的教育生态环境下，教育从封闭走向开放，从传统走向创新，知识的传授与获取不再仅限于课堂与书本，人才培养的重点也从知识教育转向创新能力培养。

根据所选的输入数据,计算各个数据之间的关联度,并将其转化为灰色关联度,灰色关联度如式(4)所示。

(4)

式(4)中,ri为灰色关联度,取值及含义同εi(k)。

2 基于GRA-IGA-BP的输电线路负荷预测模型

2.1 数据预处理

基于GRA-IGA-BP神经网络的输电线路负荷预测模型需要分析大量历史数据,通过模型训练来构建输电线路负荷与外部影响因素之间的关系。在获得历史样本数据后,将所有影响输电线路负荷的输入数据进行归一化,以消除量纲带来的影响,利于预测模型的一致性分析[13],归一化公式如式(5)所示。

(5)

式(5)中,yn为经归一化后的样本数据,y为原始样本数值,ymax和ymin分别为样本数据的最大值和最小值。

2.2 优化模型参数

遗传算法经常被用于预测模型的参数寻优方面,是一种重要的参数寻优算法,而BP神经网络是利用梯度下降的方法随机生成初始权值与阈值[14],BP神经网络性能的好与坏比较依赖于初始权值,因此,引入IGA算法优化神经网络的权值与阈值,以此来提高输电线路负荷的精度,遗传算法相关参数设置如表1所示。

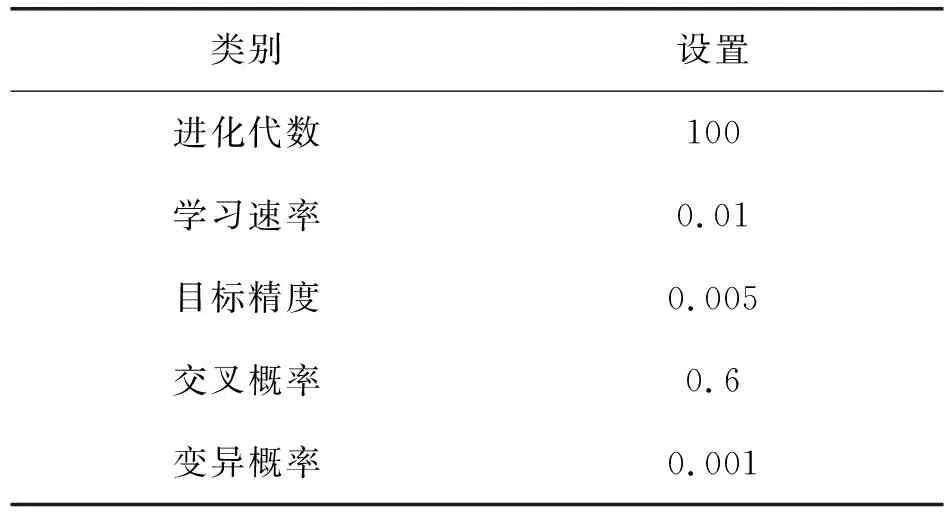
表1 遗传算法优化参数

2.3 建立IGA-BP输电线路负荷预测模型

本文利用输电线路负荷的特征信息进行灰色关联分析,提取相关性大的特征,其次为了提高输电线路负荷的预测准确度,利用改进的遗传算法优化输电线路负荷预测模型中的重要参数,输电线路负荷预测模型流程图如图2所示。

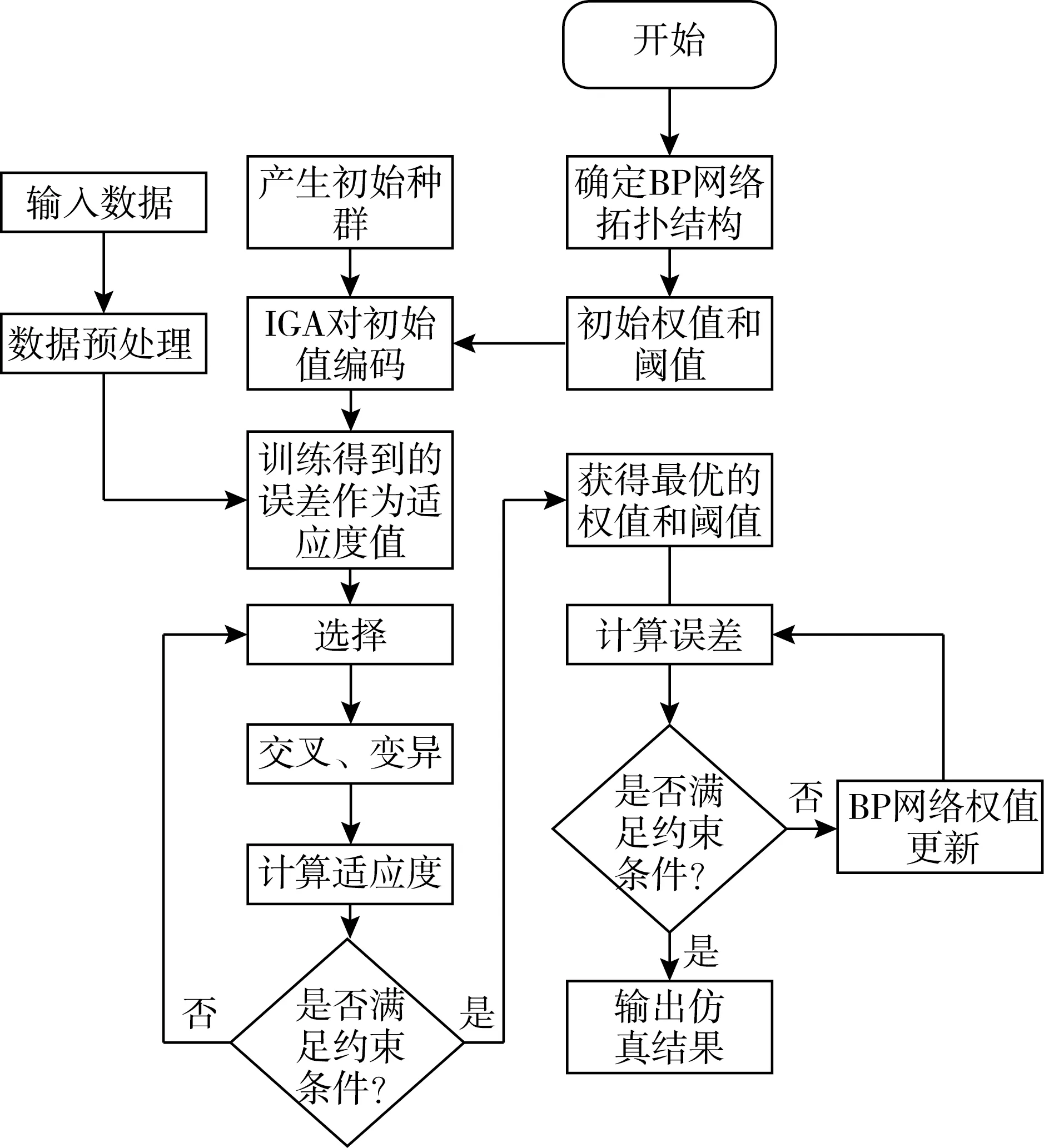
图2 IGA-BP输电线路负荷预测流程图

由图2可知,输电线路负荷预测流程主要由数据预处理、改进型遗传算法参数寻优和输电线路负荷预测构成。数据预处理是将样本数据进行归一化处理以及关联性分析。改进型遗传算法参数寻优是利用寻优算法搜索输电线路负荷预测模型中重要参数的最优解。负荷预测则是用样本数据的训练集训练模型,对划分出的测试集进行负荷预测,最终对预测结果进行分析,评估模型性能。

3 实例分析

3.1 数据来源及评价指标

选择电工数学建模竞赛数据作为本文的数据集,样本数据如图3所示,该数据集以天为采样频率,选取某地区3年内每天的负荷需求数据,共计1106天,将样本数据以8:2划分训练集和测试集。

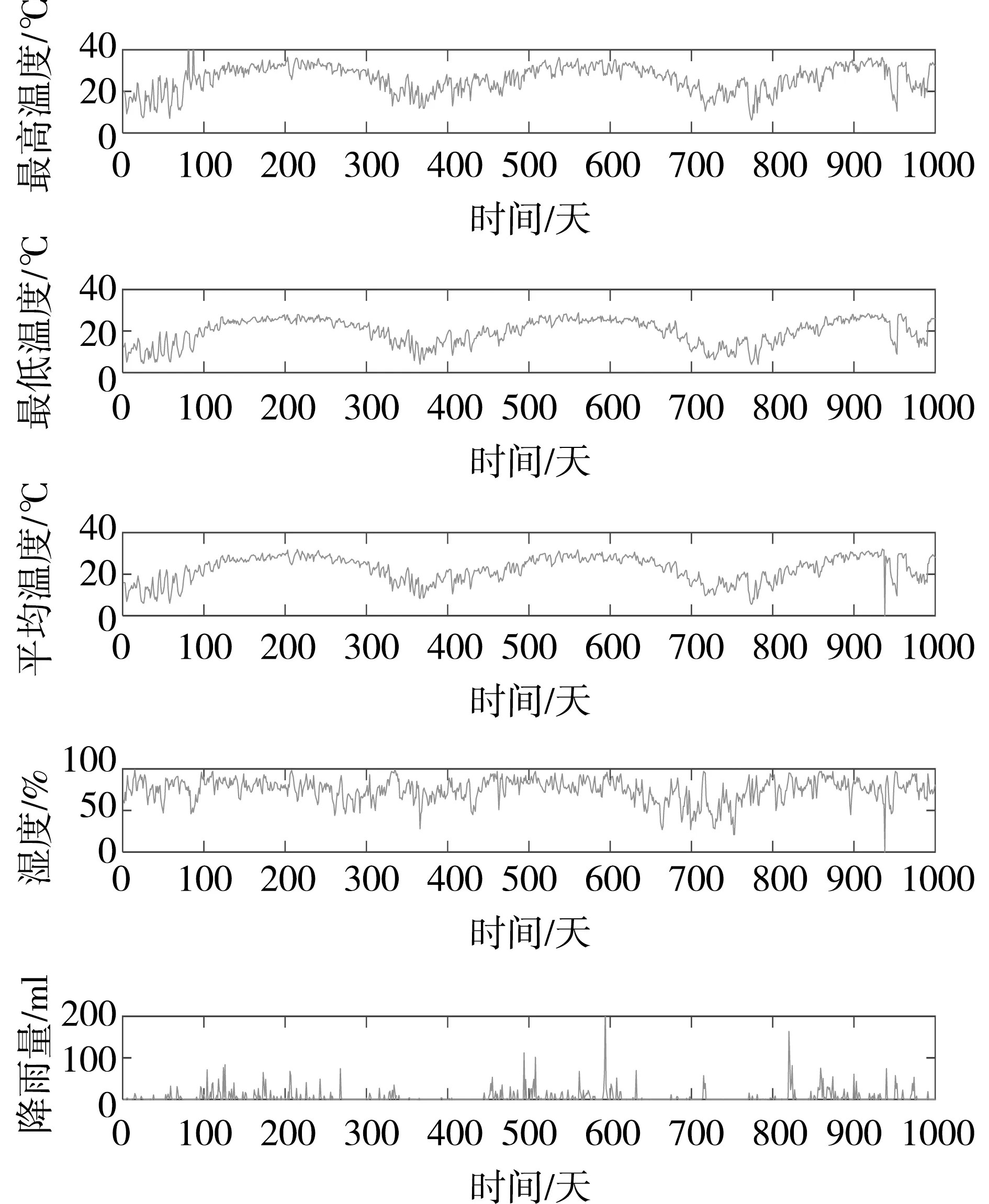
图3 日需求负荷数据

本文选取的评价指标为平均绝对百分比误差(MAE)、均方根误差(RMSE)以及拟合程度R2,MAE和RMSE的值越小代表模型估算的精度越高,R2值越大,曲线拟合效果越好。相对应的计算如式(6)-式(8)所示。

(6)

(7)

(8)

式(6)中,yp(i)表示输入样本数据第i个预测负荷值;y(i)表示输入样本数据第i个实际负荷值。

3.2 相关性分析

影响输电线路负荷的因素主要有温度、相对湿度以及降雨量等[15-16]。为了提高本文所提出的模型的预测精度以及计算效率,本文采用灰色关联分析的方法,将上述几个输入变量转化为少数几个主成分,将对比分析过后提取出来的主成分作为输电线路负荷预测模型的输入进行训练和预测,经过灰色关联分析计算过后得关联度排名如表2所示。

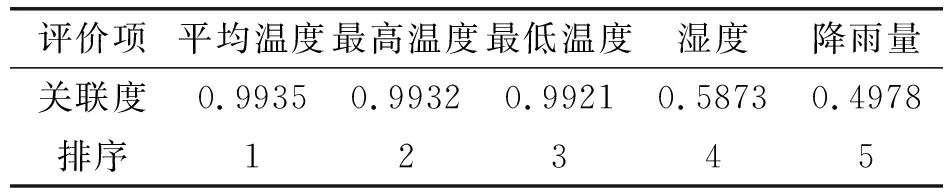
表2 关联度排名结果

关联度值高于0.5的为强相关因素,未达到0.5的为弱相关因素。由表2结果可知,平均温度、最高温度、最低温度以及湿度为影响输电线路负荷的强相关因素,而降雨量的关联度值为0.4978为弱相关因素。

3.3 实验参数设定及结果分析

利用Matlab软件平台进行仿真实验,依据处理好的输电线路负荷样本数据,构建一个基于GRA-IGA-BP的输电线路负荷预测模型。选取经关联性分析后4个相关性大的样本数据作为预测模型的输入参数,本文采用试凑法不断调整隐含层神经元个数,经过多次仿真实验尝试,效果最佳时的隐含层节点数为9个,输出层为一个神经元。

选取与输电线路负荷相关性强的因素作为本文提出的预测模型的输入参数,输电线路的负荷作为输出参数,并通过与BP预测模型以及GA-BP预测模型做实验结果的对比分析,验证本文所提出的预测模型的有效性。对IGA-BP模型具体参数进行设定:将BP神经网络的训练次数设置为1000,设置误差精度为1.0×10-6,学习率为0.01。

为了验证本文提出的预测模型的预测能力,将3种评价指标作为衡量标准,把处理好的数据输入预测模型中进行仿真实验,三种预测模型的预测值与真实值散点拟合结果如图4所示。

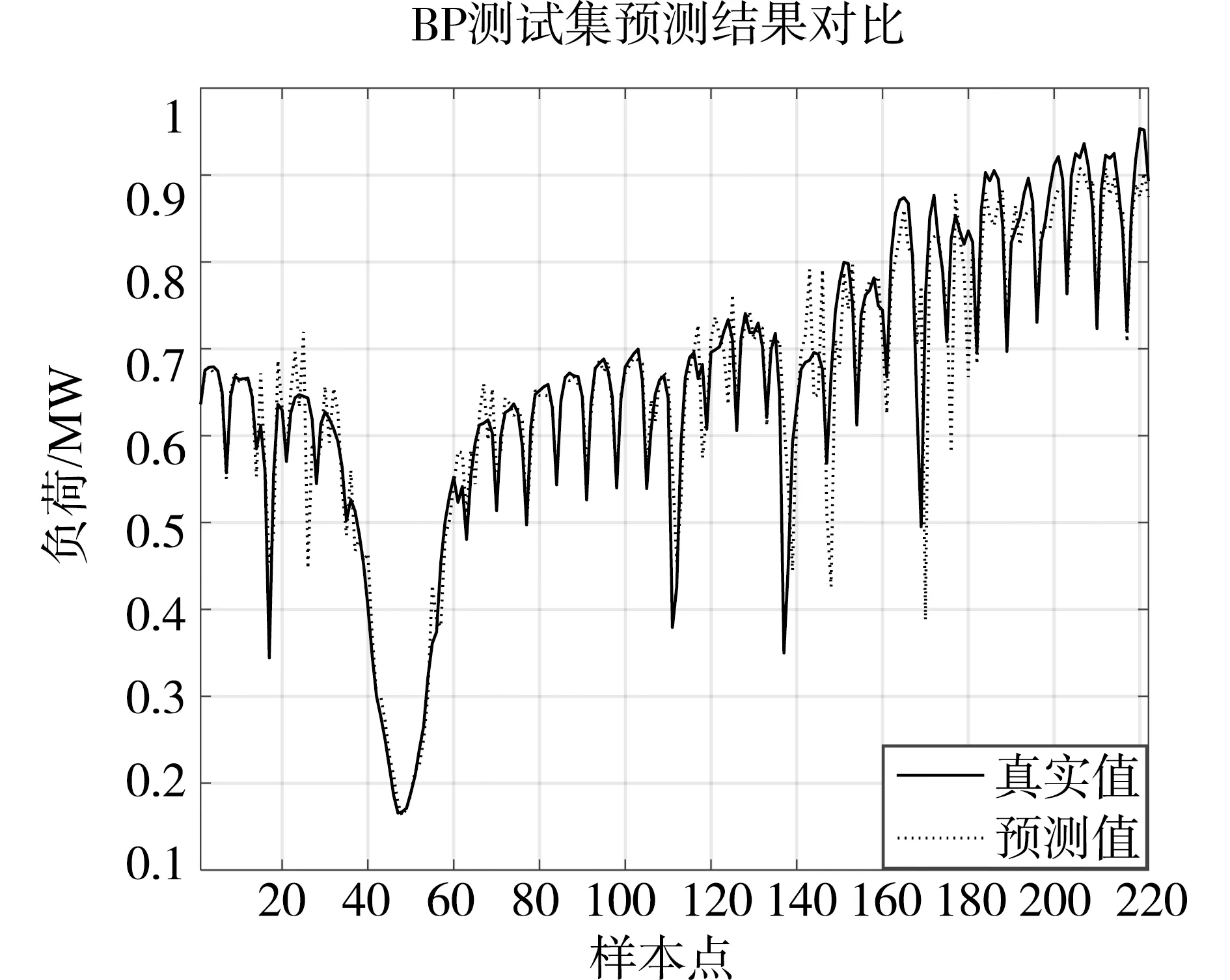
(a)BP模型预测结果

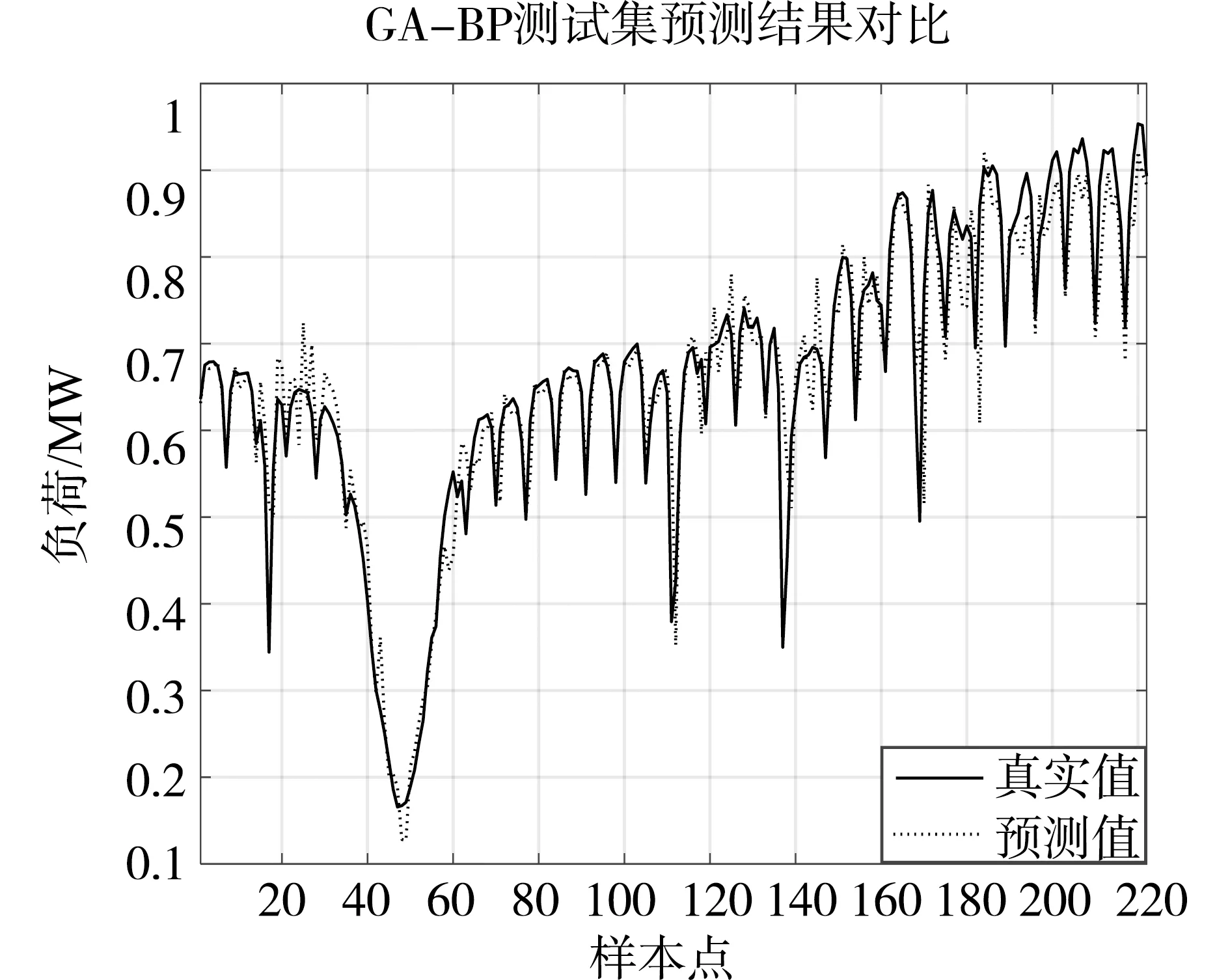
(b)GA-BP模型预测结果

(c)IGA-BP模型预测结果图4 负荷预测对比图

由图4可知,IGA-BP神经网络的预测值和实测值的拟合曲线更贴近,除此以外,优化前的BP神经网络决定系数为0.8811,其次GA-BP神经网络决定系数为0.8966,而IGA-BP神经网络的决定系数为0.9179,相较而言,利用改进的遗传算法优化后的预测模型的拟合程度更好,故可以得出本文提出的模型较其他模型具有更好的效果。三种模型预测误差对比如表3所示。

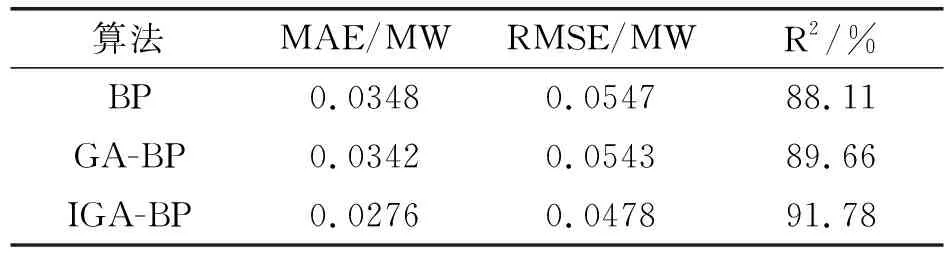
表3 三种模型预测误差对比

由表3对比可知,IGA-BP神经网络预测模型经改进型遗传算法优化后,预测结果更加接近真实值,预测效果比其他两种预测模型更好。其中BP神经网络预测模型的平均绝对百分比误差0.0348MW,均方根误差为0.0547MW,IGA-BP神经网络预测模型经改进的遗传算法优化后,预测结果更加接近真实值,预测效果比其他两种预测模型都要好。使用遗传算法优化后的GA-BP神经网络预测的平均绝对百分比误差0.0342MW,均方根误差为0.0543MW。而IGA-BP神经网络测试预测的平均绝对百分比误差0.0276MW,均方根误差为0.0478MW,两项指标参数相较于BP神经网络与GA-BP神经网络均有所降低,且拟合精度更高,这表明本文提出的IGA-BP模型的预测结果更加符合实际负荷情况,更适合于输电线路负荷预测。

参数寻优的适应度值曲线如图5所示,由图5可知,传统GA算法经30代找到一个相对稳定的数值作为全局最优解,而IGA算法能够避免产生局部最优问题,不断地寻求全局最优参数,且在第17代趋于稳定,相对于传统的GA算法而言,体现出本文提出的改进型算法具有更快的计算效率,且克服局部最优的能力更强。实验结果分析表明,本文提出的改进型遗传算法,在输电线路负荷预测模型的重要参数寻优方面更加准确,提高了预测模型的计算效率和参数的全局搜索能力。

4 结论

本研究提出了一种基于改进型遗传算法优化BP神经网络的输电线路负荷预测模型,并基于实际负荷数据进行了实验验证。首先,本文利用改进过后的遗传算法对输电线路负荷预测模型中的重要参数予以优化,寻求输电线路负荷预测模型中最优的参数,有效防止了预测模型网络训练过程中参数陷入局部最优的问题,提高了输电线路负荷预测的精度。其次,采用灰色关联分析筛选出与输电线路负荷相关性大的因素作为预测模型的输入,降低了数据维度,提高了预测模型的运算效率。本研究采用的数据未考虑具有时序属性的数据对输电线路负荷预测的影响,这也是输电线路负荷预测未来的研究方向。