露井联采作用下边坡破坏机制的研究
2023-08-08孙世国吴梦柯
孙世国,吴梦柯,关 宇
(北方工业大学 土木工程学院,北京 100144)
在露井联采的过程中,井工开采和露天开采相互影响干扰,这两种采动效应叠加形成一个复杂的动态体系。井工开采破坏了采区内的岩体,形成“三带”,这种开采效应造成了地表沉陷、边坡的不规则变形,破坏了边坡稳定性[1-7]。露天开采的推进会增加坡角,同时削弱了顶板厚度,导致坡脚处产生应力集中,对边坡稳定性不利,如果发生滑坡将会造成人员伤亡和经济损失。故研究露井联采下边坡滑移变形演化规律是十分有必要的,可以为露井联采设计和安全防控提供理论基础和技术保障。
1 工程概况
紫金山金铜矿位于福建省上杭县,属于武夷山脉,矿床分布为上部金矿下部铜矿。根据采场工程地质资料,露天边坡东帮最高标高为+1036m,坡底标高为+700m,高差为336m,边坡与地下采空区概况如图1所示。边坡岩石种类较多,采场岩体存在大量节理、断层、裂隙,对边坡的局部稳定性不利。地下采空区在+460~+570m中段,有近百个矿房[8-11]。随着露采标高的降低,地下采空区对露采产生了严重的影响。因此,需要确定露天开采顶板的极限厚度,从而保障露采边坡的稳定性和采空区的安全[12-17]。
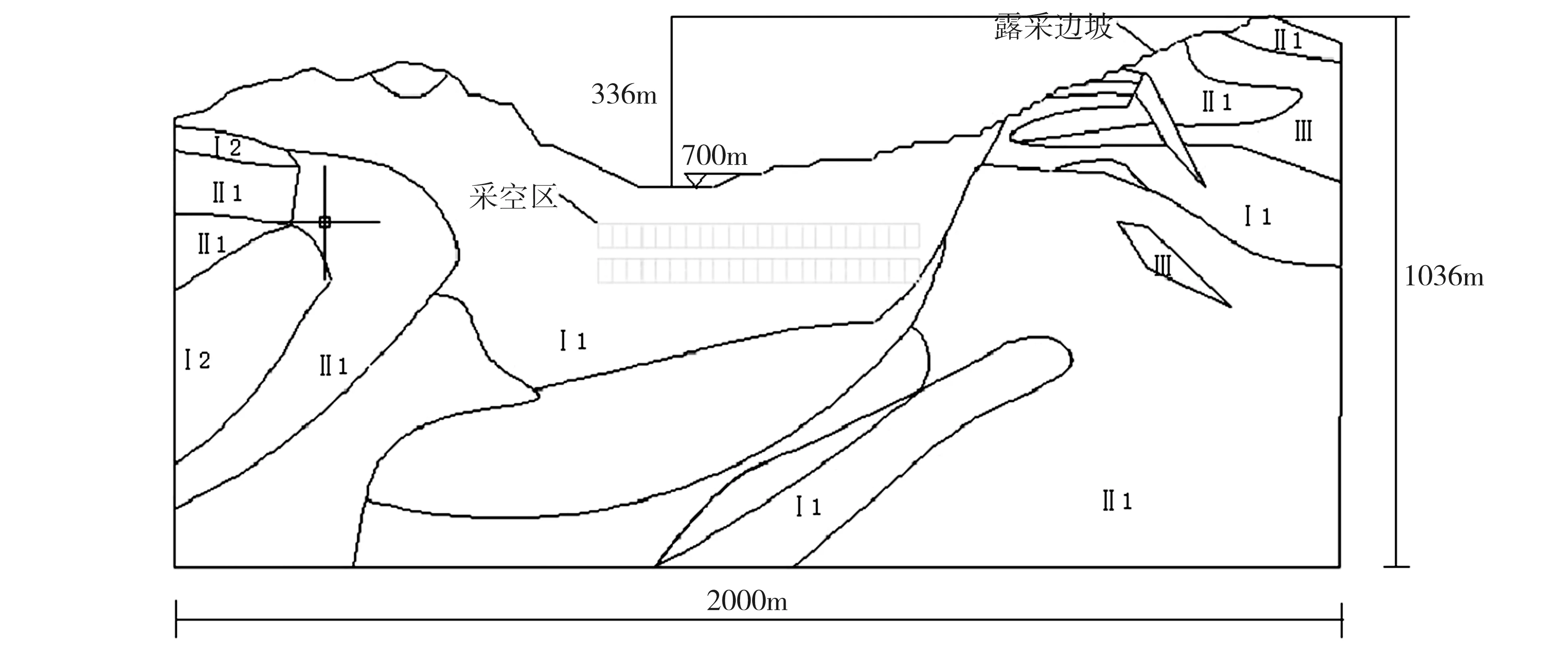
图1 采场1-1剖面图
2 露天开采不同顶板厚度对边坡稳定性的影响
根据露天开采设计方案,露采台阶高度为12m,为了确定露天开采的极限采深,分别建立了露采坑底标高为+652m、+640m、+628m、+616m、+604m时的露天与地下开采模型,对应的安全顶板厚度分别为92m、80m、68m、56m、44m。利用有限差分法对采场1-1剖面进行模拟,计算其应力应变分布和变化规律。利用极限平衡法计算出不同顶板厚度对应的边坡安全系数。模型x方向长度为2000m,Y方向的垂直高度为1036m,Z方向延伸180m。计算模型采用Mohr Coulomb屈服准则,物理力学参数如表1所示。
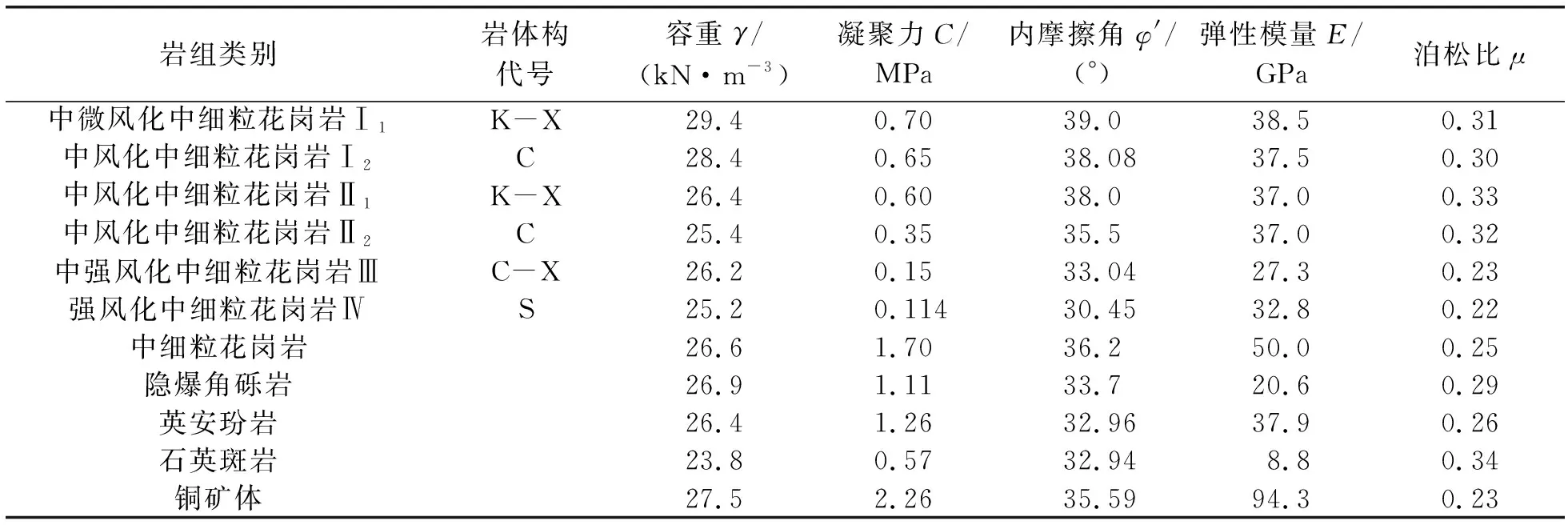
表1 采场岩土体物理力学参数表
2.1 不同顶板厚度的数值模拟结果分析
不同顶板厚度对应的顶板竖向和水平最大位移值如表2所示,顶板下沉曲线图如图2所示。可以看出,随着露采的进行,坑底标高不断降低,顶板厚度减小,顶板周围岩体在自重荷载作用下产生沉陷,顶板出现弯曲。分析竖向位移可知,地表沉陷曲线呈U形。当顶板厚度为44m时,最大下沉位移值出现在采空区右侧250m处,最大下沉位移值达到了2.69m。分析水平位移可知,随着露采境界线下降,水平位移也出现了明显增长,当顶板厚度减小至44m时,最大水平位移出现在采空区右侧50m处如图3所示,最大水平位移值为1.51m,此时水平位移值较大,边坡可能会出现失稳破坏。
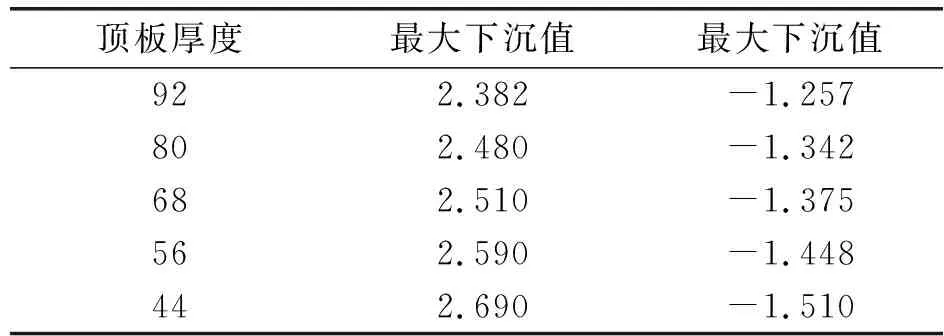
表2 顶板最大位移值表 m

图2 顶板下沉曲线图
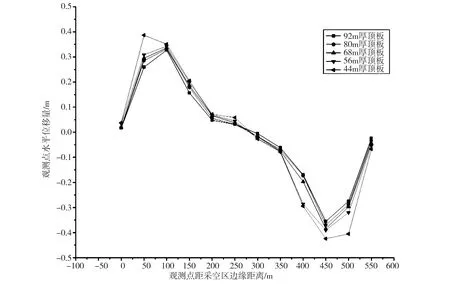
图3 顶板水平位移图
图4和图5是厚度为96m和44m的顶板水平应力云图,通过对比分析可知,顶板厚度为96m时,顶板覆岩在自重应力的影响下产生弯曲,从地表到采空区上侧由压应力逐渐转变为拉应力。随着开采的进行,顶板厚度减小至44m时,顶板所受拉应力减小,压应力增加。这是由于随着顶板厚度削弱,顶板自重应力减小,两侧边坡坡脚处产生应力集中的同时两侧边坡对顶板的挤压作用增强,抵消了一部分由自重应力产生的拉应力。

图4 顶板厚96m水平方向应力云图
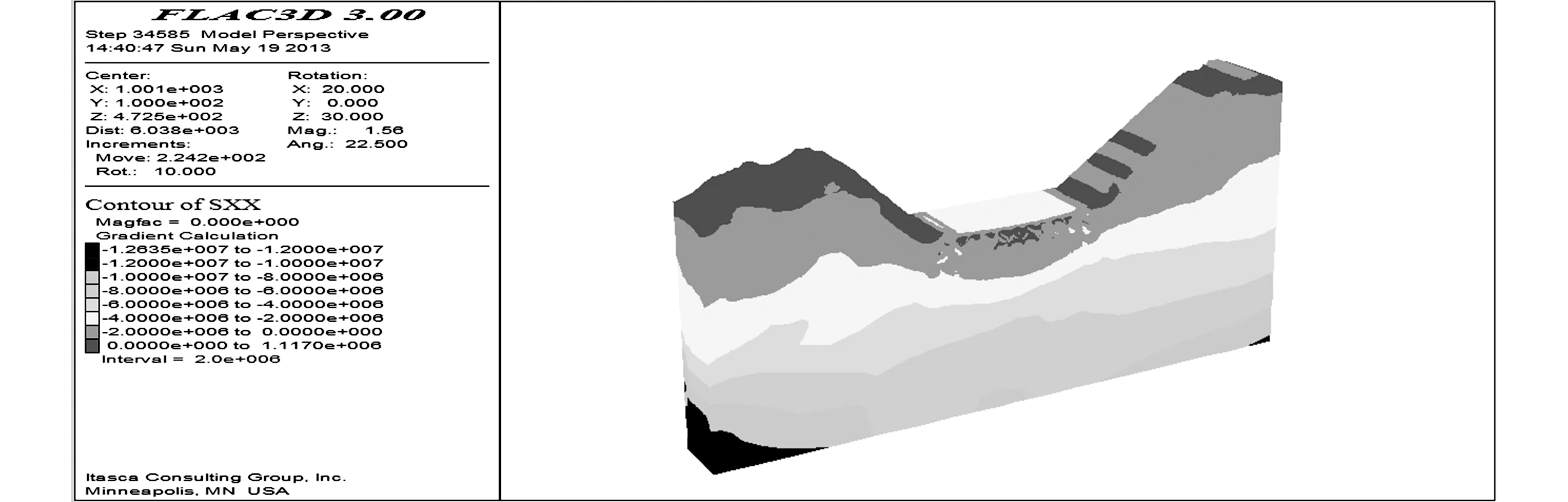
图5 顶板厚44m水平方向应力云图
综上所述,顶板的破坏主要有两种模式,一种是顶板在自重应力的影响下产生的弯曲,拉应力在此时起主导作用,当岩体的抗拉强度低于拉应力时,顶板遭到破坏。另一种是随着露采的推进,顶板厚度削弱,坡脚处产生应力集中,顶板拉应力减小,压应力增加,两侧边坡坡脚和顶板连接处发生压剪破坏,导致边坡不稳定。通过对比分析,顶板厚度为68m和44m的塑性区破坏图,如图6所示,随着开挖的进行,两侧边坡坡脚处和顶板的塑性区范围扩大,当顶板厚度为44m时,坡脚处塑性区和顶板处塑性区产生贯通,边坡坡脚易产生压剪破坏。

(b)顶板厚44m塑性区破坏图图6 不同顶板厚度塑性区破坏图
2.2 东帮边坡稳定性的数值模拟分析
露采边坡最高点标高为1036m,露采坑底标高为700m,岩体物理力学参数如表1,分别计算当采空区顶板厚度为92m、80m、68m、56m、44m时边坡的安全系数,不同顶板厚度对应的边坡安全系数如表3所示。
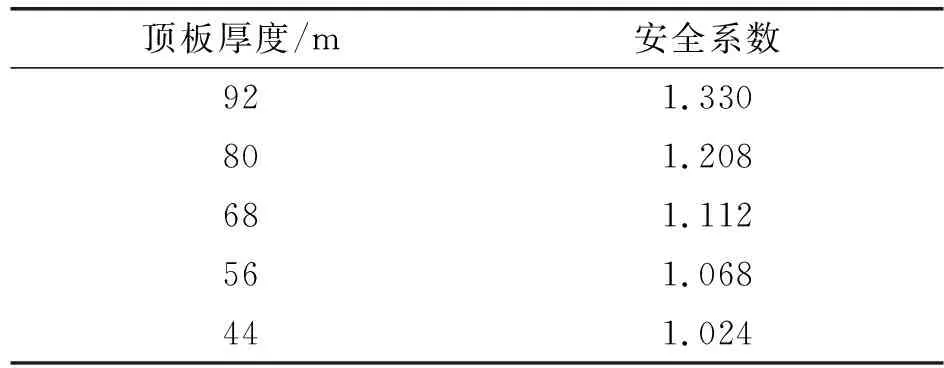
表3 东帮边坡不同顶板厚度模型边坡安全系数表
由计算结果可知,随着露采的推进,露采警戒线逐渐降低,顶板厚度削弱,边坡的坡角也随之增加,边坡的安全系数逐渐降低。当采空区顶板厚度为68m坡角为31°时,边坡安全系数为1.112小于边坡的安全设计要求1.2,说明边坡此时此刻处于一个临界的稳定状态。
综上,顶板厚度为68m时,边坡塑性区尚未贯通,边坡稳定系数为1.112,边坡处于一个临界状态,因此68m为顶板的极限厚度;小于68m边坡水平和竖向位移进一步增加,坡脚处出现压剪破坏,顶板塑性区范围扩大与边坡坡脚处塑性区产生贯通,对边坡稳定性不利。
3 井工开采对岩质边坡稳定性的影响
露井联采中露天边坡的沉陷很大程度上是井工开采所造成的,井工开采分为顺坡开采和逆坡开采,本节在考虑孔隙水压力条件下分析逆坡开采时的边坡稳定性。部分采动的坡面如图7所示,滑面分为未受开采影响的BC段和受开采影响下沉的AB段。设滑体重W,滑面倾角为β,α,l1,l2分别为两段滑面的长度。N1,N2与T1,T2分别表示法向力和切向力。
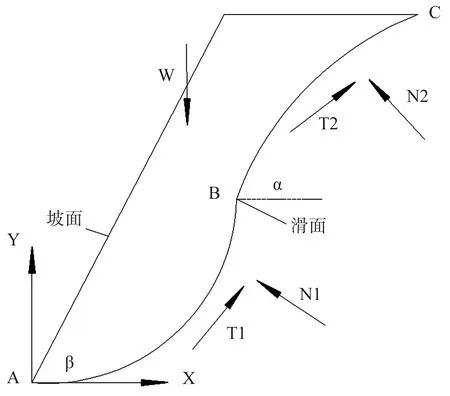
图7 滑体未完全采动时受力示意图
AB,BC面上的抗滑力分别如式(1)、式(2)所示。
(1)
(2)
式(1)、式(2)中:Fs—滑坡稳定性系数,当该比值大于1时,坡体稳定;等于1时,坡体处于极限平衡状态;小于1时,边坡即发生破坏;
φ′—内摩擦角;
c′—粘聚力C的1/Fs倍;
u—摩擦系数。
由∑Fy=0可得:
W=N1cosβ+N2cosα+T1sinβ+T2sinα
(3)
由∑Fx=0可得:
N1sinβ+N2sinα=T1cosβ+T2cosα
(4)
将式(1)、式(2)分别代入式(3)、式(4)得:
(5)
式(5)中:A1=Wsinα;
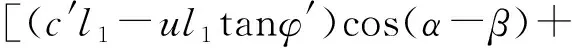
(c′-utanφ′)l2+Wtanφ′cosα];
C1=(c′-utanφ′)l1sin(β-α);
D1=sin(α-β);
E1=tan2φ′sin(β-α)。
在开采初期滑体重心在BC滑面上,滑体即将滑动时,滑体与滑面AB的接触应力为0,因此,令式(5)=0可得:
A1Fs12+B1Fs1+C1=0
(6)
解得:
(7)
随着开采的推进,滑体重心将落在AB段上,设滑体重心到B点的水平距离为l0,AB长为l1′,由滑体受力对B点的力矩平衡得:
N1l1′=Wl0
(8)
由式(6)、式(8)解得:
A2Fs22+B2Fs2+C2=0
(9)
式(9)中:
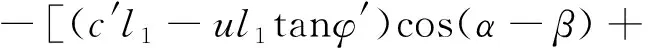
(c′-utanφ′)l2+Wtanφ′cosα]
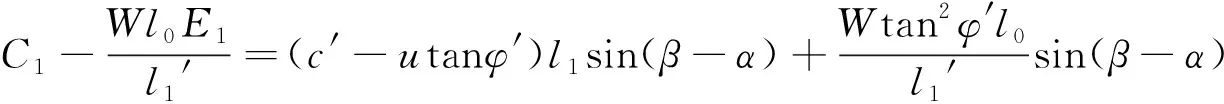
解得:
(10)
如图8所示,当滑面较长部分滑体被完全开采时,将滑面分成被完全开采的AB段、未被完全开采的BC段和未受影响的CD段来研究。BC段滑面的倾角为γ,AB段与CD段滑面的倾角都为δ,l3、l4、l3为滑面AB、BC、CD的长度,N3、N4、N5、T3、T4、T5为法向力和切向力。
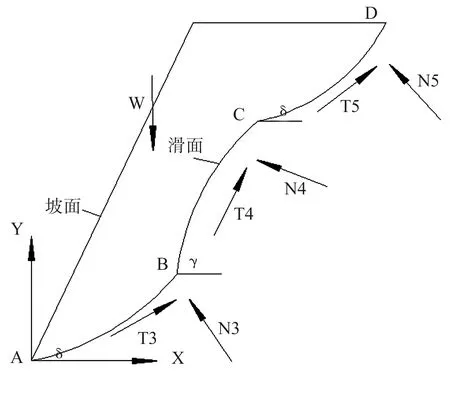
图8 滑体达充分采动时受力示意图
设此时滑体的安全系数为Fs3,则三段滑面的抗滑力为:
(11)
(12)
(13)
由∑Fy=0可得:
W=N4cosγ+(N3+N5)cosδ+T4sinγ+
(T3+T5)sinδ
(14)
由∑Fx=0可得:
N4sinγ+(N3+N5)sinδ=T4cosγ+
(T3+T5)cosδ
(15)
将式(11)、式(12)和式(13)分别带入式(14)和式(15)得:
(16)
式(16)中:A3=Wsinδ
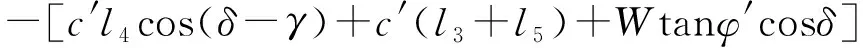
D3=sin(δ-γ)
E3=-tan2φ′sin(γ-δ)
令式(16)等于0,于是可得稳定性系数Fs的计算式如式(17)所示。
A3Fs32+B3Fs3+C3=0
(17)
解得:
(18)
对Fs1、Fs2、Fs3进行对比分析。当开采地质条件一定时,表达式中的参数β与δ、α与γ、tanφ′、c′、W、l1与l3、l2与l4、l是相等的,不受开采推进的影响。完全开采时l5是一个定值,因此Fs3是一个常数。只有l1、l2为变化值。Fs1和Fs2都是随着l1和l2的增大而减小。当Fs1、Fs2、Fs3三种情况都可能发生时:
(1)在Fs1与Fs2的临界状态时,l2=0,l2=l1,由式(8)得:Fs1=Fs2
(2)在Fs2与Fs3的临界状态时,l2=l5,得:
(19)
因为A3>0,C3>0,D3<0,E3<0,所以得:
(20)
因此得:
(21)
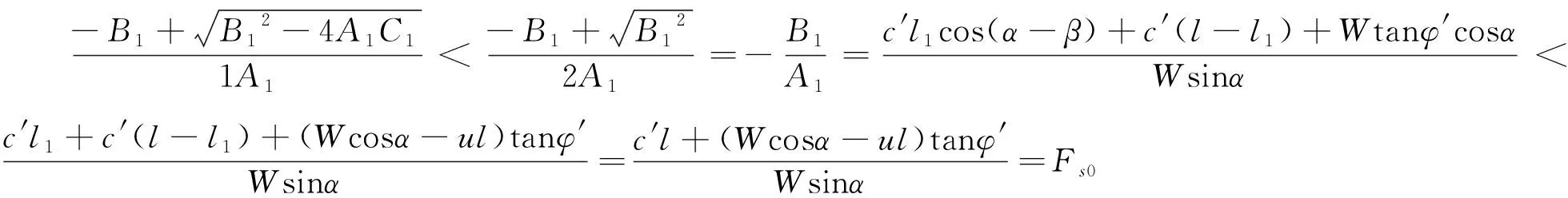
(22)
综上分析可得,随着井工开采的推进,边坡的稳定性系数也随之减小,当滑体被完全开采时,边坡稳定性系数会先达到一个最小值随后将增加,此时稳定性系数为定值Fs3,边坡稳定性系数不再发生改变。分析三种情况的边坡稳定性系数Fs1、Fs2、Fs3可知,井工开采的推进降低了稳定性系数。
4 结论
(1)随着露天开采的推进,顶板厚度逐渐削弱,顶板覆岩的破坏模式由拉弯破坏转变为压剪破坏;边坡坡脚处产生应力集中,对边坡的稳定性造成不利影响。当顶板厚度小于68m时,边坡与顶板连接处容易产生塑性区贯通且边坡稳定性系数低于安全设计要求,因此综合分析顶板的极限厚度为68m。
(2)利用极限平衡法建立了逆坡井工开采影响下边坡稳定性系数的计算公式。由计算公式可知,当未完全开采滑体时,边坡稳定性系数Fs1、Fs2随着开采的推进而降低;当滑体被完全开采时,安全系数Fs3不变。Fs3大于滑体被完全开采的安全系数Fs2和Fs1。
