基于SUMO仿真的交叉口信号配时优化研究

张 军,卞云豪,刘克非,张建祥

(安徽理工大学 1.人工智能学院;2.机械工程学院,安徽 淮南 232001)

随着我国经济发展和城市化进程加快,近十年来私人小轿车的数量快速增加,城市交叉口配时方案与交通需求之间不断产生尖锐矛盾,而信号交叉口是城市道路建设中的重要组成部分,起着城市路网的重要枢纽作用,由于某些交叉路口的通行能力不足,而造成交通拥堵问题日益严重。因此,在交叉口现有的道路交通基础设施之上,对交叉口进行配时方案优化,可以最大限度地提高交叉口的通行效率,减少等待时间、延误等,从而达到缓解交叉口交通拥堵的目的,对解决智慧城市道路交通拥堵问题具有非常重要的意义,可以在一定程度上提高道路通行能力,减少延误,保证行车畅通[1]。同时,近些年来,我国各中大型城市均存在不同程度的空气污染问题,而汽车尾气是其中主要污染源之一。在城市道路中,交叉口处的尾气排放最为明显。因此,为了环境友好,减少空气污染,缓解信号交叉口处车辆尾气排放不易消散的问题也十分重要。

在单点交叉口信号控制和车道功能划分方面:马晓旦等通过实际案例在VISSIM里进行仿真,并比较了方案优化前后的交叉口运行情况,证明了采用VISSIM仿真软件对交叉口进行优化,能有效地减少路口交通拥堵,提高交叉口的通行能力[2]。李世武等运用TSIS微观交通仿真软件,对长春市的工农路口交通状况进行了优化仿真模拟,并进行了交通优化设计[3]。胡成龙等人还利用VISSIM软件对益阳大街-龙洲路交叉口进行了详细的调查和分析,并利用Synchro软件对该路段进行了实时仿真,并进行了相应的优化。优化后的配时方案对交叉口拥堵问题的解决起到了较好效果[4]。

本文主要用SUMO(simulation of urban mobility)微观仿真软件进行实验验证,从2001年起,SUMO作为第一个可运行版本在德国宇航中心内部的许多工程上得到应用。SUMO是一个连续的微观城市道路交通仿真软件,具备城市道路交通仿真架构和模型基础。其主要由德国宇航中心和交通运输研究中心开发的。该软件始于2000年,SUMO作为一个开源的交通仿真软件主要是给研究交通的组织提供一个实现和评判自己算法的工具,被广泛地应用于城市交通状况仿真[5-7]。本文以淮南市洞山东路与淮河大道北段交叉路口为例,运用SUMO交通微观仿真模型对该交叉口进行建模仿真,利用Webster算法优化现状信号配时,通过平均延误、平均等待时间、平均速度和CO总排放等指标评估改善效果。

1 交通现状调查

1.1 交叉口现状

洞山东路与淮河大道北段交叉口位于淮南市田家庵区淮河大道与洞山中路、洞山东路的交会处。东进口包括六车道,分别为一条右转专用车道、四条直行车道和一条左转专用车道;南进口为四车道,包括一条右转专用车道、两条直行车道和一条左转专用车道;西进口设有六条车道,包括两个右转专用车道,三条直行车道和一条左转车道。北进口包括五条车道,分别为一条右转专用车道、一条右转直行混合车道、一条直行专用车道、一条由左转直行混合车道和一条左转专用车道构成。

该地段交叉路口的位置信息是南北方向的淮河大道为淮南市贯穿南北的主干道,洞山东路向东通往大通区,洞山西路向西与泉山路交叉,途径淮南市博物馆。另一方面,该交叉口处于淮南老政务核心区域,被吾悦广场、室外步行街等大型商场包围,附近设有多个公交站点,途经的公交车辆较多,同时向北为城北高架,这一系列因素造成了洞山东路与淮河大道北段交叉口处日常的车流量和人流量都特别大。

1.2 实际交通流量调查

本文在对洞山东路与淮河大道北段交叉口实际交通进行测量时,采用了人工观察。此路口为十字路口,由四条进口道组成,各进口道分别各设一位调查员负责观察各入口车道的车流。并分别记录右转、直行和左转的机动车交通量,并且分车种地进行记录,流量调查时间段为工作日早高峰(7:30—8:30)。交通量换算以小型客车为标准车型,在进行车型的换算时应以符合表1中的规定换算系数为准[8]。即将调查的交通量按照《城市道路工程设计规范》(CJJ37-2012)规定的车种换算系数折算成标准当量小汽车[9],得到洞山东路与淮河大道北段交叉口的交通量高峰小时交通量如表2所示。

表1 车种换算系数

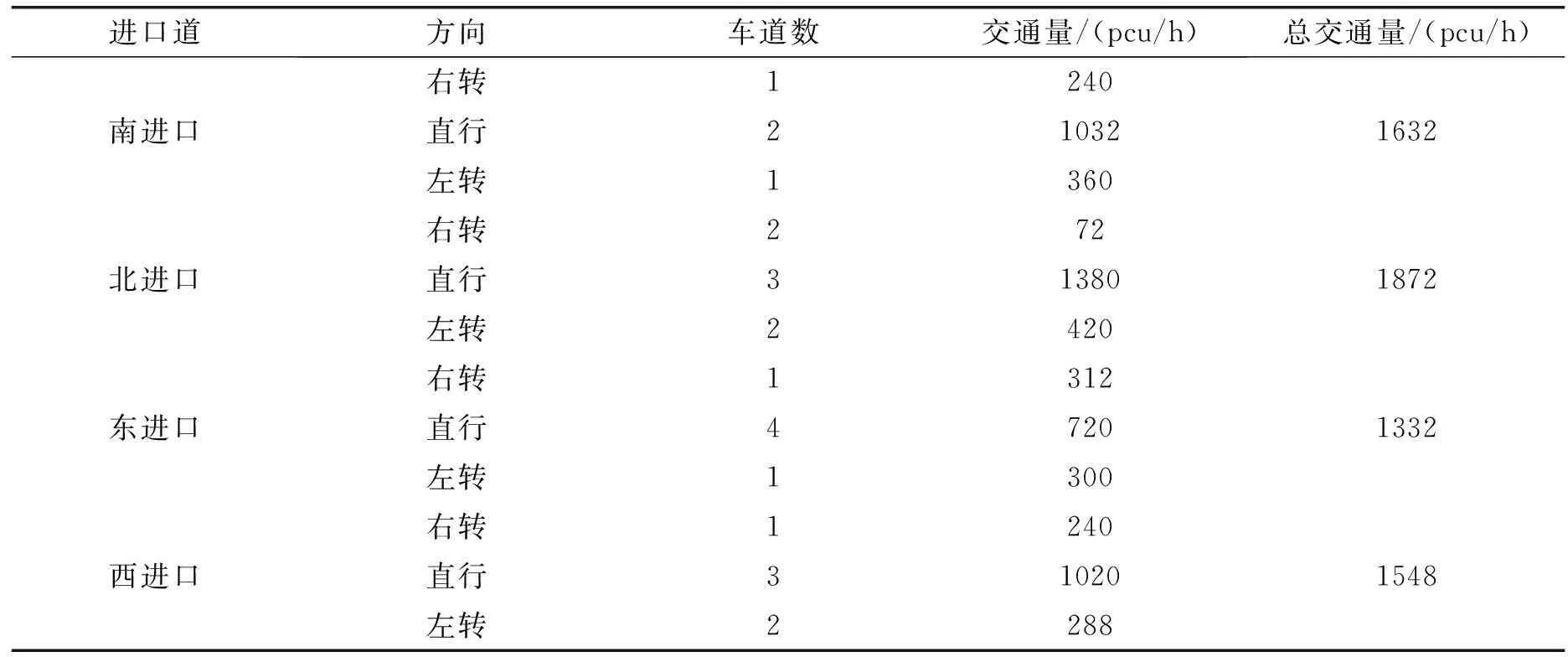
表2 洞山东路与淮河大道北段交叉路口的早高峰小时交通流量表

1.3 交叉口现状信号相位配时方案调查

该交叉口现状的信号控制方式采用定时周期控制,一个信号总周期为176s,绿信比是0.93,一共四个相位,现状相位配时如表3所示,交叉口的右转车辆不受信号灯的控制。

表3 现状相位配时表

2 信号配时优化

2.1 韦伯斯特延误模型

Webster法可以最大限度减少车辆延误,用该方法求得最佳总周期时长,是目前交通部门定时控制中被用来确定单点交叉口信号配时方案的常用方法之一。在20世纪50年代,Webster法的计算公式由韦伯斯特和柯布先提出,后来由R·金伯等人的改进而来[10]。它的延误公式是利用蒙特卡罗(Monte Carlo)模拟法把随机延误和平均延误一起进行标定得到,第i相位每辆车的平均延误时间如式(1)所示。

(1)

式(1)中,di为第i相位交叉口进出口道处的车辆平均延误;gei为第i相位的有效绿灯时间;C为信号总周期时长;qij为第i个相位第j个进口道实际到达的当量交通量;xij为第i个相位第j个进口道的饱和度。

一个周期内交叉口的车辆平均延误时间如式(2)所示。

(2)

韦伯斯特延误模型能够较好地反映信号交叉口配时、交通量大小、饱和度与车辆延误之间的定量关系。

2.2 配时优化过程

利用Webster配时方法对淮南市洞山东路与淮河大道北段交叉口信号配时方案进行计算和优化,配时方案具体设计过程如下。

(1)相位设计。洞山东路与淮河大道北段交叉口相位设计为:第一相位东西直行、第二相位东西左转、第三相位南直行加左转、第四相位北直行加左转,共四个相位,不考虑右转。

(2)计算饱和流量。饱和流量是指一次连续的时间内连续的车辆通过交叉口进口道停车线的最大流量,即连续车队加速到正常行驶速度时,一定时间内通过进口道停车线的稳定车流量,用S表示,单位为pcu/h。饱和流量随道路几何条件、渠化方式、车流状况以及配时方案等情况而异,但与绿灯信号的时间长短基本无关[11]。因此,配时方案信号相位的设置情况主要影响道路实际饱和流量大小。计算公式如式(3)所示。

(3)

式(3)中,ht车头时距,一般为了安全,车头时距取2s以上。

(3)总损失时间L的计算如式(4)和式(5)所示。

L=tR+tL·4

(4)

tL=ts+tb

(5)

式(4)和式(5)中,tR为全红时间(s);tL为损失时间;ts为汽车起动损失时间(s);tb为制动损失时间,取1s。

本文不设全红时间,其中损失时间是由启动损失时间加制动损失时间。

(4)流量比的计算如式(6)和式(7)所示。

(6)

(7)

式(6)和式(7)中,yi为各相位交通流量比;q为实际交通量(pcu/h);Y为所有相位关键车流的流量比之和。

若流量比之和大于0.9,由近似配时法可得信号总周期超过200s,交叉口等待通行车辆等待时间过长,应重新选择相位方案,比如采取增加专用相位等措施来缓解车辆经过交叉口处的不必要等待。若流量比之和小于0.9,则当前相位方案可以使用。

(5)最佳周期C0的计算如式(8)所示。

(8)

式(8)中,C0为最佳周期长度(s)。

(6)计算有效绿灯时间gei。

有效绿灯时间是指将一信号周期内该相位车队以饱和流率通行所对应的绿灯时长。有效绿灯时间的计算如式(9)和式(10)所示。

Gei=C0-L

(9)

(10)

式(9)和式(10)中,Gei为总有效绿灯时间,gei为各相位有效绿灯时间。

(7)各相位绿灯时间的计算如式(11)所示。

gi=gei+tL-ty

(11)

式(11)中,gi为第i相位的绿灯显示时间,ty为黄灯时长(一般取3s)。

2.3 优化后的信号配时方案

使用Webster法优化后的总信号周期为132s,各相位的配时方案如表4所示。

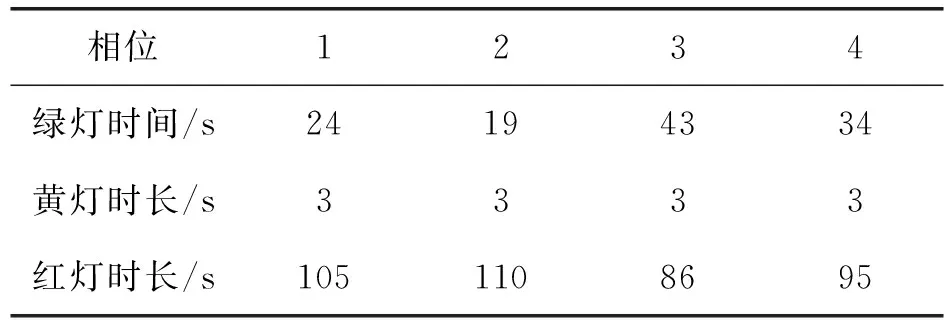
表4 优化后的信号配时表

3 SUMO交叉口仿真及分析

采用SUMO仿真软件来建立微观交通仿真系统,针对实测的交通需求下的现状配时方案和优化后的配时方案进行分析。

3.1 车辆运动模型

SUMO具有多种车辆运动模型可供选择,本文使用的车辆运动模型是SUMO默认的Krauss模型,该模型是微观、空间上连续、时间上离散的安全车速跟驰模型,具有优异的性能,是由Stefan Krauss提出的[12-14]。

Krauss模型假定司机在1秒内做出了响应,这5个参数的意义是:

a:车辆最大加速度(m/s2);

b:车辆最大减速度(m/s2);

Vmax:车辆最大行驶速度(km/h);

l:车身长度(m);

ξ:驾驶熟练系数ξ∝(0,1),其值越小表示驾驶员越熟练。

安全车速的计算如式(12)所示。

(12)

式(12)中,vl(t)为t时刻前车的速度;vf(t)为t时刻后车的速度;g(t)为t时刻前车与后车的间距;Γ为驾驶员的反应时间(一般取1秒)。

在SUMO仿真软件中,Krauss模型来实现,如式(13)所示。

(13)

因为上面的式子所计算的车辆的安全速度可能会超出公路所能行驶的最高速度,该模型实现时取上面三个值中的最小值,称其为期望车速,其具体表述如式(14)所示。

v(t)=min[vmax,v+a·tl,vsafe]

(14)

式(14)中,tl为仿真步长。如果驾驶员的驾驶技术使车辆无法达到所需的速度,计算出车辆的速度,即设定车辆的速度减去驾驶员的缺陷值、车辆加速能力(加速度)和随机数的乘积,同时确保车辆的速度大于0,从而得出最后的Kraus模型如式(15)所示。

v(t)=max[0,vdes-δ·a·rand( )]

(15)

计算下一仿真的车辆位置如式(16)所示。

Pl+1=pl+v(t)·tl

(16)

3.2 交叉口仿真

SUMO软件仿真流程如图1所示,应用SUMO自带的路网编辑工具NetEdit对淮南市洞山东路与淮河大道北段交叉路口进行路网建模,绘制出的路网如图2所示。

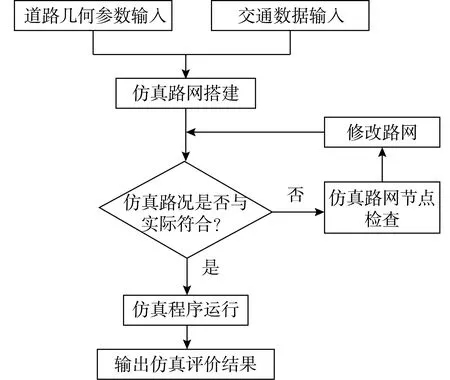
图1 仿真流程图

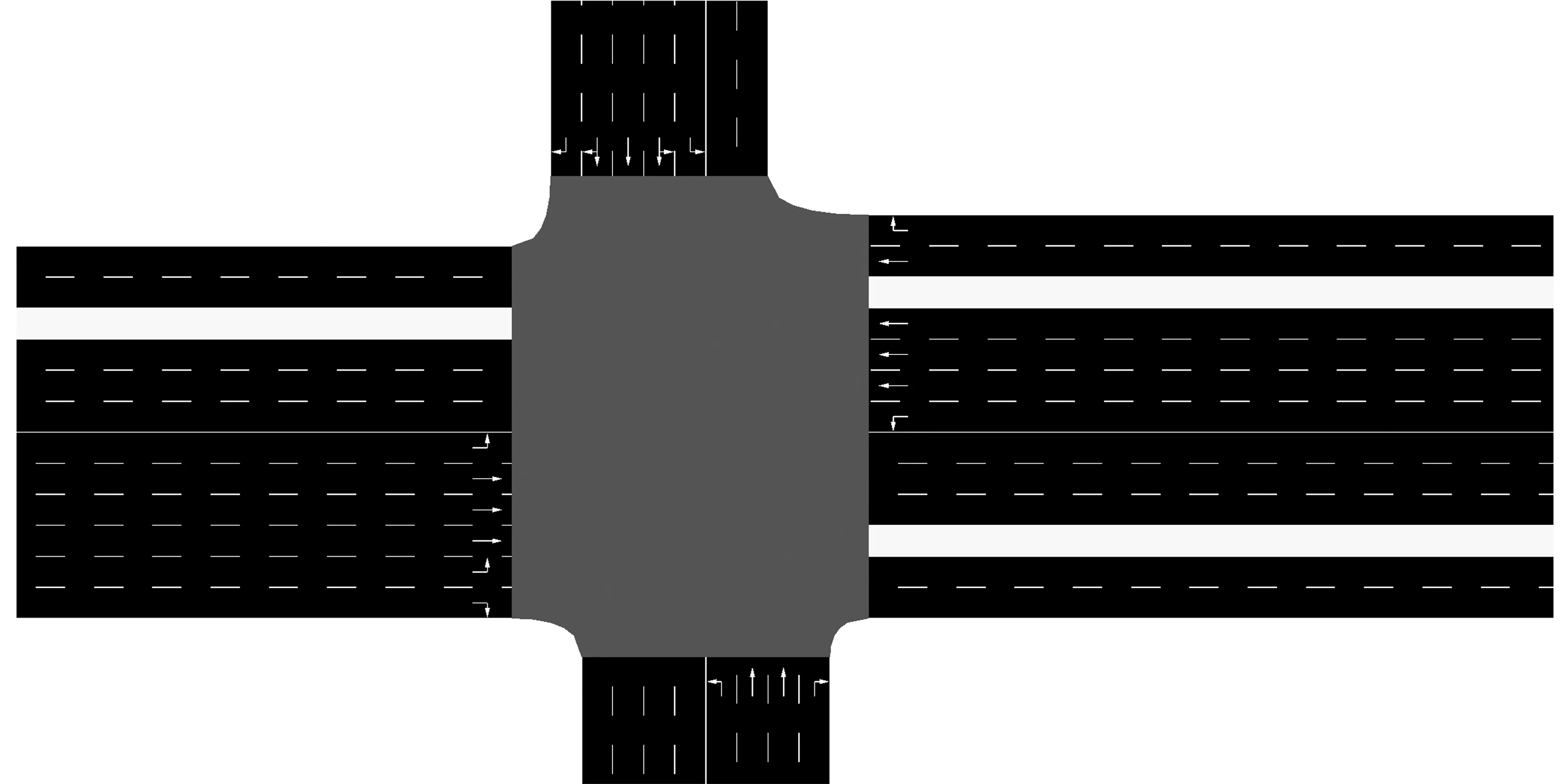
图2 洞山东路与淮河大道北段交叉口路网图

在SUMO仿真软件的各个模块中输入交叉口实测数据以及优化前后配时方案,SUMO仿真过程是根据洞山东路与淮河大道北段交叉口现状几何参数特性、实地测量的交通需求值等来进行的,并且分别建立起优化配时方案前后的仿真程序,仿真过程如图3所示。

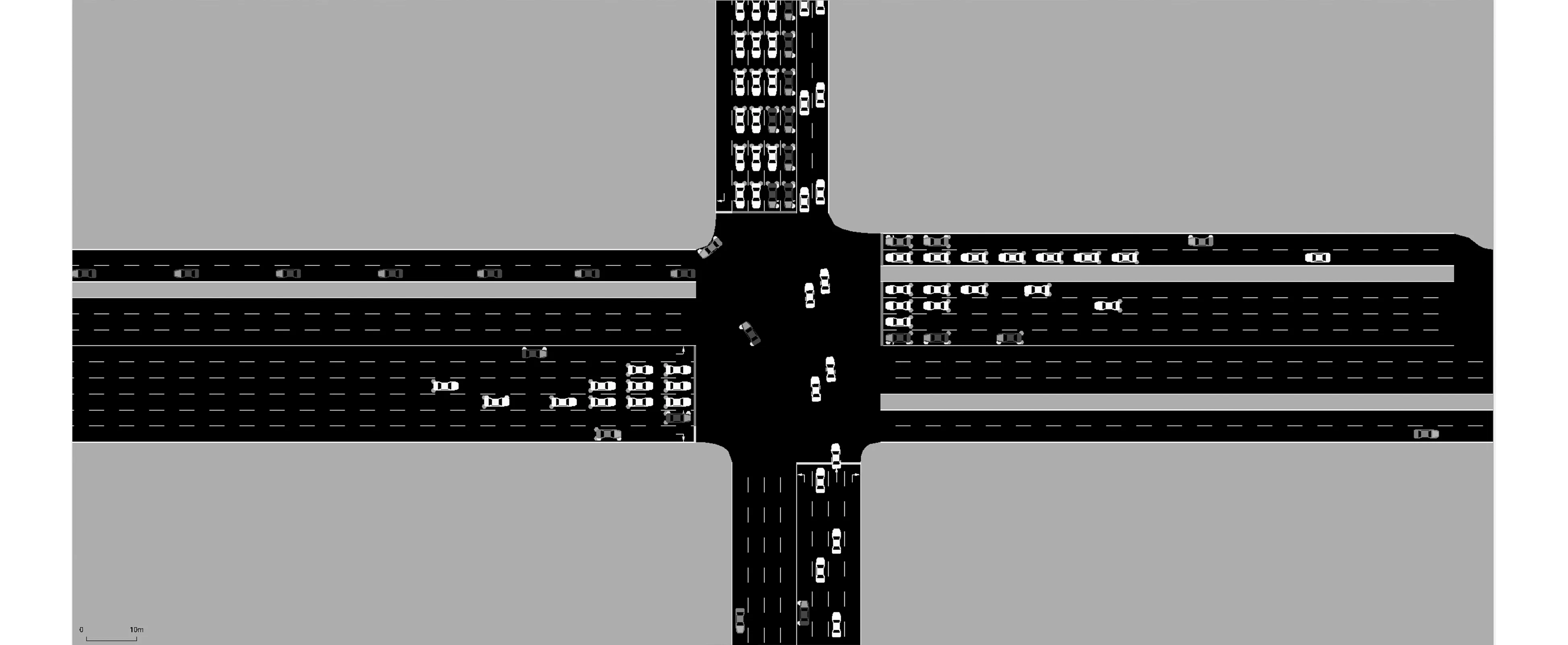
图3 洞山东路与淮河大道北段交叉路口SUMO仿真过程

3.3 仿真实验结果分析与对比

为了评价对比优化前后配时方案的效果,本文选取了平均延误、平均等待时间、平均速度和CO排放为评价指标。

SUMO仿真结束后会生成交叉口仿真结果输出文件output-tripinfos,然后对输出文件进行数据分析。其中,对车辆等待(waiting)时间、速度(speed)等输出结果分别进行求平均值得到交叉口平均等待时间、平均速度,车辆CO排放输出结果进行求和得到交叉口总排放。得到的配时优化前后仿真结果如表5所示。从表中可以得出:应用了Webster算法进行优化之后,洞山东路与淮河大道北段交叉口信号总周期变为132s,相对于现状缩短了25%;平均延误变为50s/veh,相对于现状下降了23%;平均等待时间缩短至7.43s,比现状下降了36%;平均速度变为8.71m/s,提高了10%;CO总排放减少了16%。

表5 Webster优化结果与现状对比

4 结论

针对淮南市洞山东路与淮河大道北段交叉口的早高峰出行时期交通拥堵问题,利用了Webster算法对该交叉口进行配时优化,并在此基础上,采用SUMO微观交通仿真软件仿真了配时优化前和优化后的交叉口车流。优化后结果表明,周期变为132s,比现状缩短了25%;平均延误下降了23%;平均等待时间下降了36%;平均速度提高了10%;CO总排放减少了16%。提高了该交叉口的通行效率,减少了交叉口尾气排放,为交通部门制定城市信号配时方案提供了一定的依据。